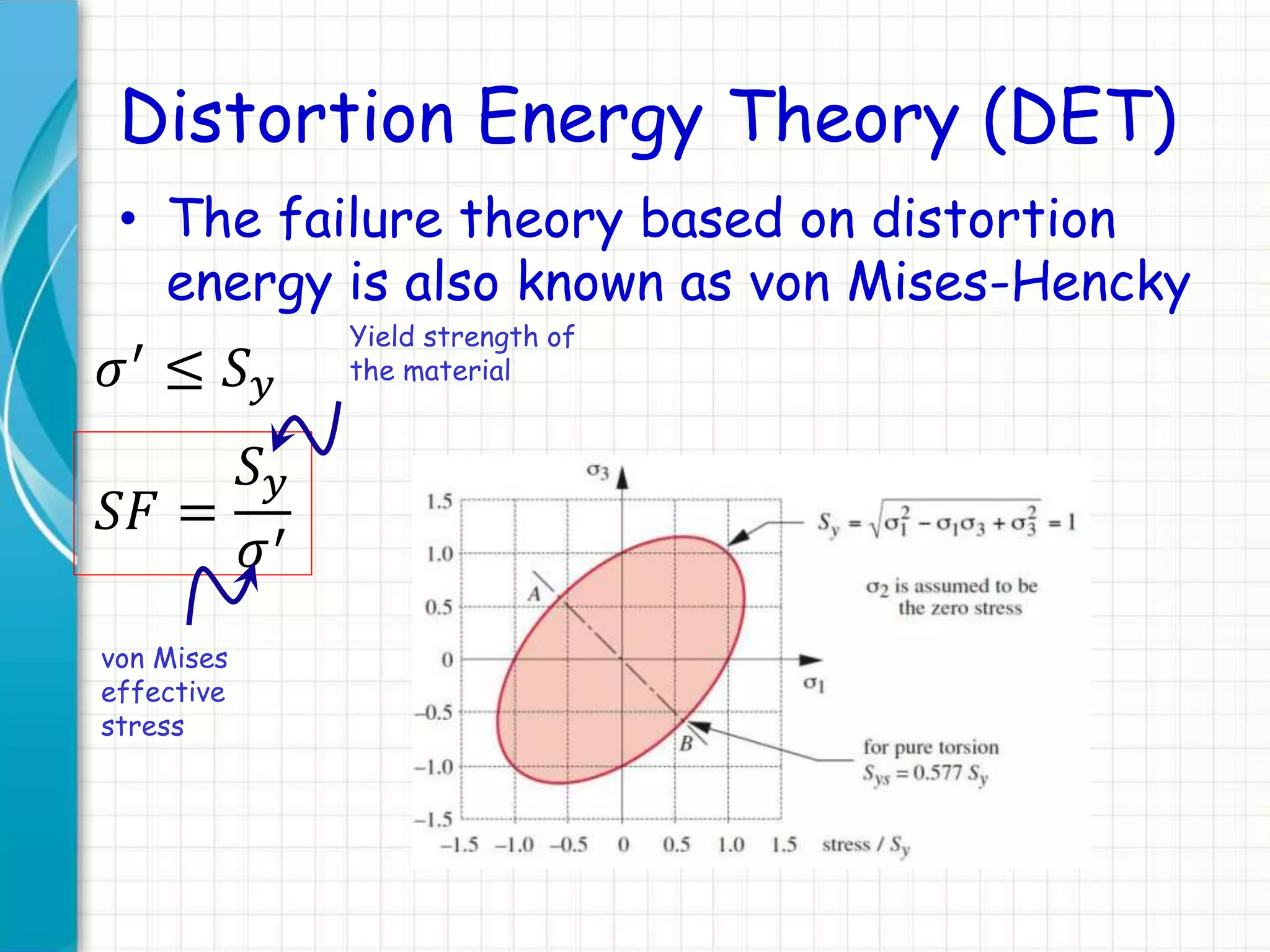
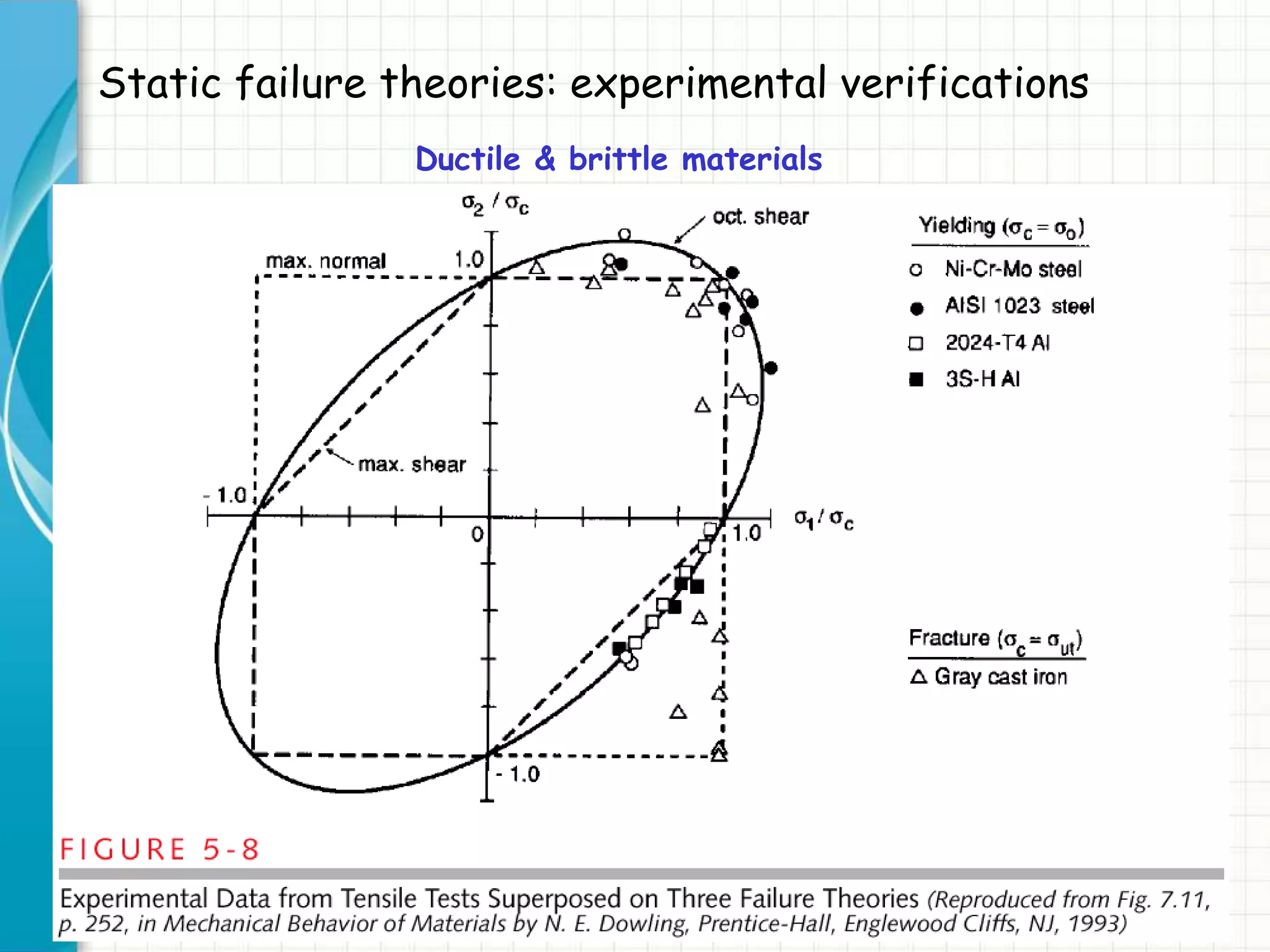
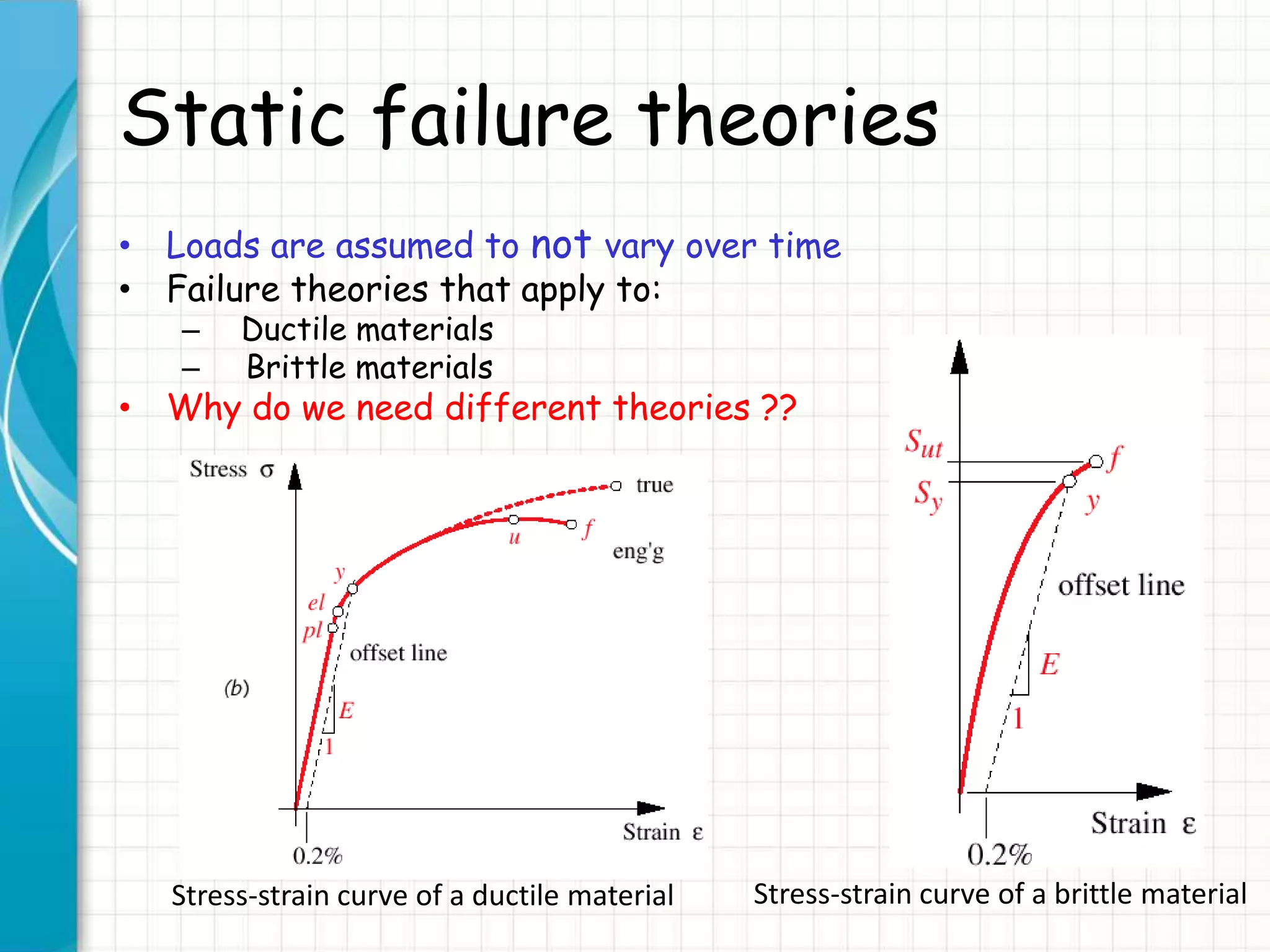
This document discusses static failure theories for analyzing machine components under loading. It begins by asking why parts fail and explaining that failure depends on the material properties and type of loading. It then covers different failure modes and the need for separate theories for ductile and brittle materials. The key static failure theories presented are maximum normal stress theory, maximum shear stress theory, distortion energy theory, and their applications to ductile and brittle materials. Examples are provided to illustrate Mohr's circle analysis and applying the theories.

1. MACHINE DESIGN: STATIC
FAILURE THEORIES
Dr. Himanshu Chaudhary
Associate Professor
Dept. of Mech. Eng.
MNIT Jaipur

2. Static failure theories
• Why do parts fail?
• You may say “Parts fail because their stresses exceed
their strength”
• Then what kind of stresses cause the failure: Tensile?
Compressive? Shear?
• Answer may be: It depends.
• It depends on the material and its relative strength in
compressive, tension, and shear.
• It also depends on the type loading (Static, Fatigue,
Impact) and
• presence of the cracks in the material

3. Static failure theories
• The failure may be elastic or fracture
• Elastic failure results in excessive
deformation, which makes the machine
component unfit to perform its function
satisfactorily
• Fracture results in breaking the component
into two parts

4. Static failure theories
• Question: How do one compare stresses
induced to the material properties?
– Generally machine parts are subjected to combined
loading and to find material properties under real
loading condition is practically not economical
– Thus, material properties are obtained from simple
tension/torsion test
– These data like Syt, Sut etc are available in form of
table (Design Data Book)

5. Static failure theories
• Theories of failure provide a relationship between the
strength of machine component subjected to complex
state of stress with the material properties obtained
from simple test (Tensile)
Strength of machine
component subjected
to complex state of
stress
Strength of
standard component
subjected to
uniaxial state of
stress

6. Static failure theories
• Loads are assumed to not vary over time
• Failure theories that apply to:
– Ductile materials
– Brittle materials
• Why do we need different theories ??
Stress-strain curve of a ductile material Stress-strain curve of a brittle material

7. Static failure theories: Tension test
Why nearly 0o ??
Failure along
principal shear stress
plane
Failure along
principal normal
stress plane
Cast iron has C
between 2.1% to 4%
and Si between 1%
and 3% C contents
less than 2.1% are
steels.

8. Static failure theories:
Compression test
Why doesn’t it fail ?? Why does it fail ??
Why nearly 45o ??
Does not
“fail”
Shear failure

9. Failure along principal shear stress plane Failure along principal normal stress plane

10. Static failure theories
• In general, ductile, isotropic materials are limited by
their shear strengths.
• Brittle materials are limited by their tensile strengths.
• If cracks are present in a ductile material, it can
suddenly fracture at nominal stress levels well below
its yield strength, even under static loads.
• Static loads are slowly applied and remain constant
with time.
• Dynamic loads are suddenly applied (impact), or
repeatedly varied with time (fatigue), or both.

11. Static failure theories
• In dynamic loading, the distinction between
failure mechanisms of ductile and brittle
materials blurs.
• Ductile materials often fail like brittle
materials in dynamic loading.

12. Static failure theories
• Total strain energy theory
• Distortion energy theory
• Pure shear-stress theory
• Maximum shear-stress theory
• Maximum normal stress theory (limited application)
Accepted failure theories that apply to ductile materials:
Accepted failure theories that apply to brittle materials:
• Maximum normal stress theory (even material)
• Maximum normal stress theory (uneven material)
• Coulomb-Mohr theory
• Modified Mohr theory

13. Maximum Normal Stress Theory
• Credited to the English scientist and educator
W. J. M. Rankine (1802–1872)

14. Maximum Normal Stress Theory
• This predicts that failure of machine component, subjected to complex loading,
occurs if the maximum normal principal stress tends to exceeds the uniaxial
tensile yield (ductile) or the ultimate tensile strength (brittle) of the material
• Providing a square failure boundary with Sy as the principal stress for ductile
materials
• Note: not a safe theory for ductile materials
Exercise: Draw
failure envelop
for two
dimension
case?

15. Maximum Normal Stress Theory
• Let 1, 2, 3 are the principal stresses at the
critical point in component due to applied
loading, and let 1> 2> 3
• Then failure occurs when
𝜎1 ≥ 𝑆 𝑦𝑡 𝑜𝑟 𝜎1 ≥ 𝑆 𝑢𝑡
If we want to include uncertainty of data available and loads
acting on the component, i.e., factor of safety, then to avoid
failure:
𝜎1 =
𝑆 𝑦𝑡
𝐹𝑆
𝑜𝑟 𝜎1 =
𝑆 𝑢𝑡
𝐹𝑆

16. Maximum Shear-Stress Theory
• The oldest failure theory, originally proposed
by the great French scientist C. A. Coulomb
(1736–1806)
• Tresca modified it in 1864, and J. J. Guest
• Validated by experiments around 1900
• For these reasons the maximum-shear-stress
theory is sometimes called the Tresca-Guest
theory

17. Maximum Shear-Stress Theory
This theory states that a material subjected to any combination of loads will fail (by
yielding or fracturing) whenever the maximum shear stress exceeds the shear strength
(yield or ultimate) of the material. The shear strength, in turn, is usually assumed to be
determined from the standard uniaxial tension test.
Exercise: Draw
hexagonal
failure envelop
for two
dimesion case?

18. Static failure theories
This theory states that failure occurs when:
Ductile materials: maximum shear-stress theory
𝑆 𝑦𝑠 = 0.5𝑆 𝑦
(Failure occurs when maximum
shear stress
exceeds the shear stress at
yield in pure tension)
Mohr’s circle:
pure tension
𝑆𝐹 =
𝑆 𝑦𝑠
𝜏 𝑚𝑎𝑥
𝜏 𝑚𝑎𝑥 ≤ 𝑆 𝑦𝑠

19. Static failure theories
Ductile materials: maximum shear-stress theory
Providing a hexagonal failure envelope that is more conservative than
the distortion energy theory

20. Maximum Shear Stress Theory

21. Maximum Shear Stress Theory

22. Static failure theories
Ductile materials
Total strain energy U:
Elastic range
assuming stress strain
curve is linear upto
yield point
𝑈 =
1
2
𝜎𝜀
𝑈 =
1
2
𝜎𝜀 =
1
2
(𝜎1 𝜀1 + 𝜎2 𝜀2 + 𝜎3 𝜀3)
Principal stresses and
strains
𝜀1 =
1
𝐸
(𝜎1 − 𝜐𝜎2 − 𝜐𝜎3
𝜀1 =
1
𝐸
(𝜎2 − 𝜐𝜎3 − 𝜐𝜎1
𝜀1 =
1
𝐸
(𝜎3 − 𝜐𝜎1 − 𝜐𝜎2
where

23. Static failure theories
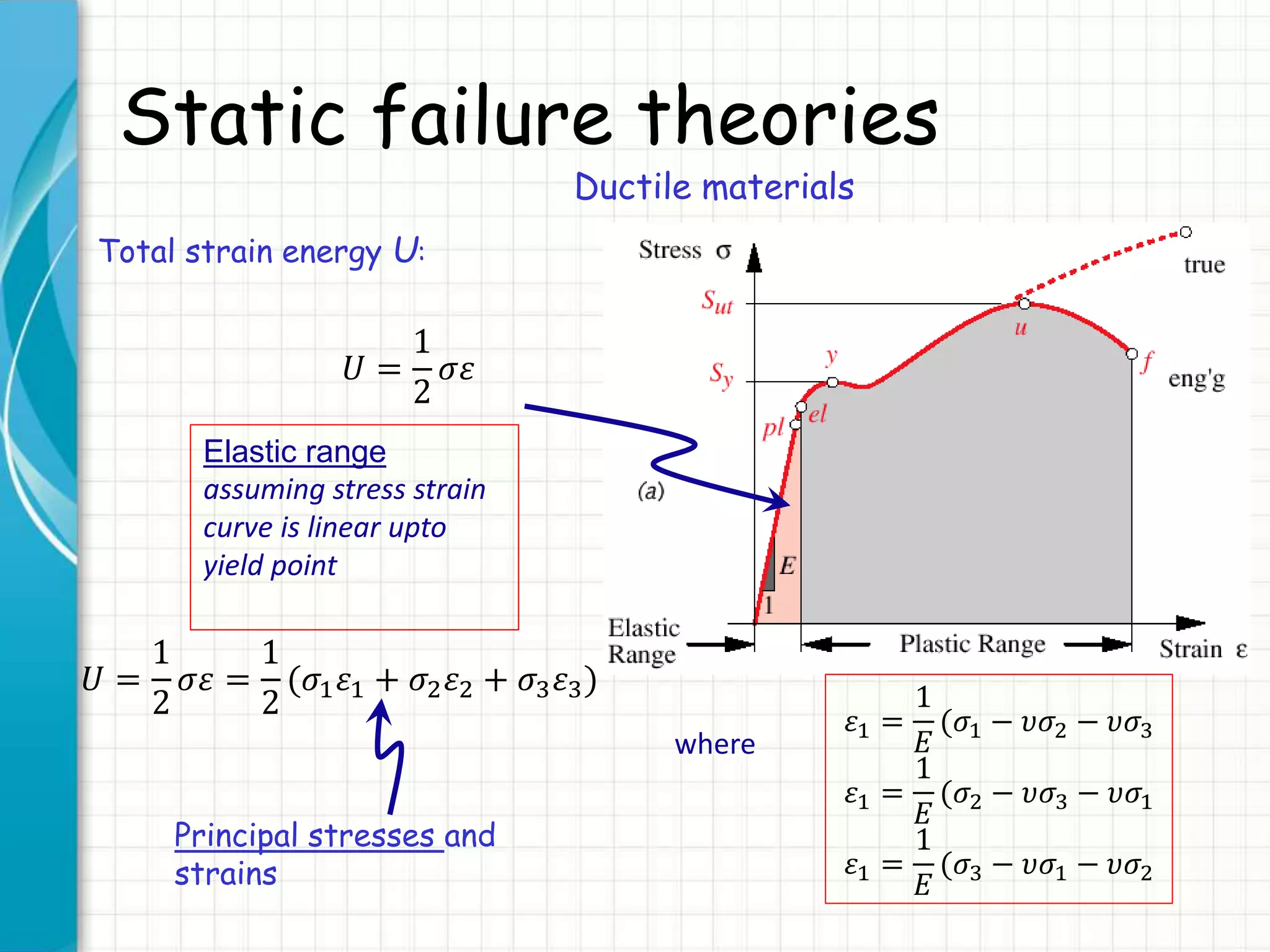
Ductile materials: total strain energy
Using previous expressions, total energy is:
𝑈 =
1
2
𝜎𝜀 =
1
2𝐸
[𝜎1
2
+ 𝜎2
2
+ 𝜎3
2
− 2𝜐(𝜎1 𝜎2 + 𝜎2 𝜎3 + 𝜎3 𝜎1)
which can be expressed as 𝑈 = 𝑈ℎ + 𝑈 𝑑
Hydrostatic energy Deformation energy
𝑈ℎ =
3
2
(1 − 2𝜐)
𝐸
𝜎ℎ
2
𝜎ℎ =
𝜎1 + 𝜎2 + 𝜎3
3
Obtained by setting:
𝑈ℎ = 𝑈(𝜎1 = 𝜎2 = 𝜎3 = 𝜎ℎ)
𝑈 𝑑 =
1 + 𝜐
3𝐸
[𝜎1
2 + 𝜎2
2 + 𝜎3
2
−(𝜎1 𝜎2 + 𝜎2 𝜎3 + 𝜎3 𝜎1)]
Obtained by setting:
𝑈 𝑑 = 𝑈 − 𝑈ℎ

24. Static failure theories
Ductile materials: distortion energy theory
𝑈 𝑑 =
1 + 𝜐
3𝐸
[𝜎1
2 + 𝜎2
2 + 𝜎3
2 − (𝜎1 𝜎2 + 𝜎2 𝜎3 + 𝜎3 𝜎1
If uniaxial yield stress state (failure state):
𝜎1 = 𝑆 𝑦
𝜎2 = 0
𝜎3 = 0
Therefore:
𝑈 𝑑 =
1 + 𝜐
3𝐸
𝑆 𝑦
2 Using uniaxial yield
stress state (failure
state)

25. Static failure theories
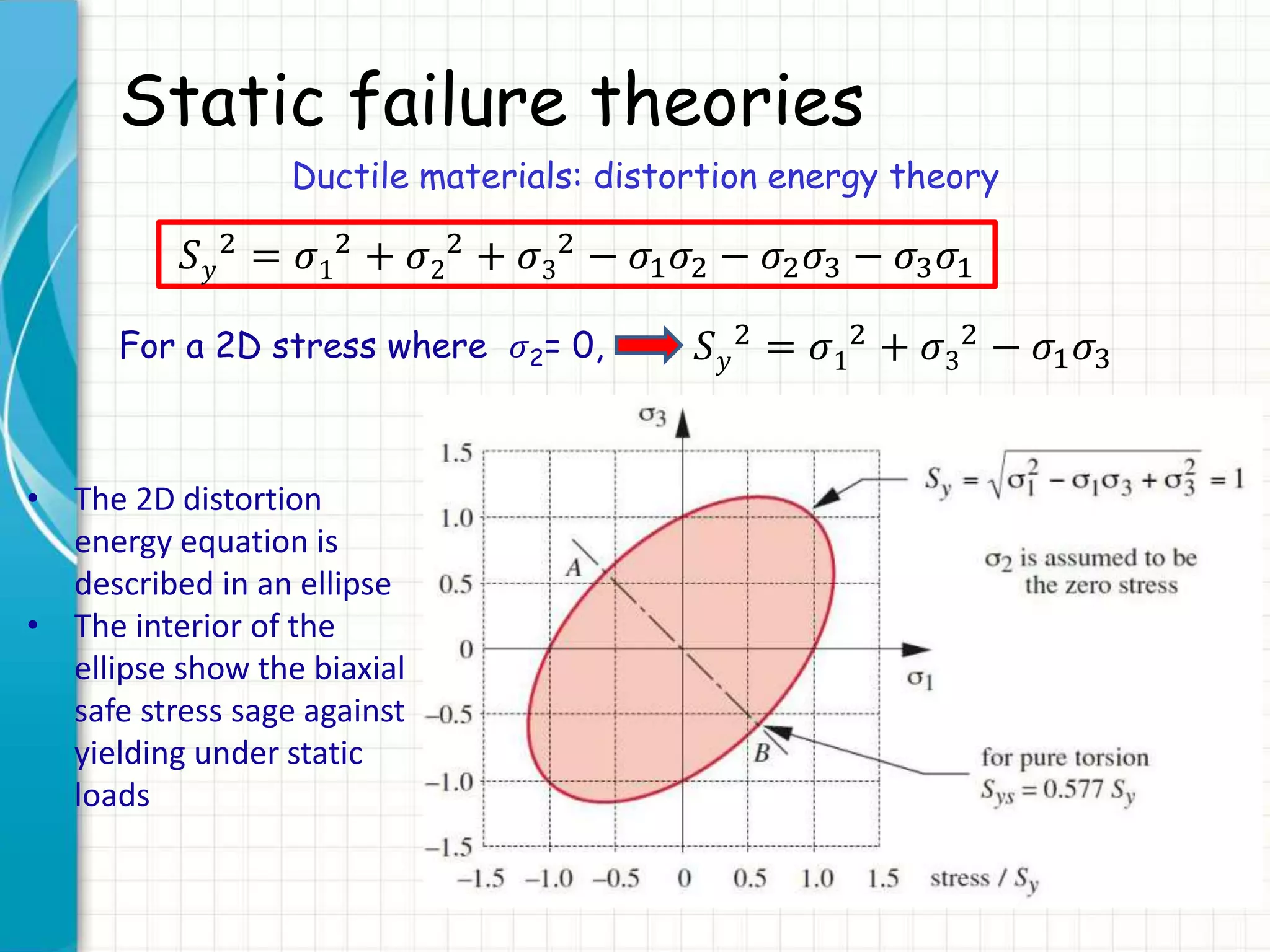
Ductile materials: distortion energy theory
𝑈 𝑑 =
1 + 𝜐
3𝐸
[𝜎1
2 + 𝜎2
2 + 𝜎3
2 − 𝜎1 𝜎2 + 𝜎2 𝜎3 + 𝜎3 𝜎1 ]
For any other state of stresses:
Failure criterion is obtained by setting:
1 + 𝜐
3𝐸
[𝜎1
2
+ 𝜎2
2
+ 𝜎3
2
− (𝜎1 𝜎2 + 𝜎2 𝜎3 + 𝜎3 𝜎1] ≤
1 + 𝜐
3𝐸
𝑆 𝑦
2
Distortion energy:
uniaxial stress at
yield
Distortion energy:
any other state of
stresses
𝜎1
2 + 𝜎2
2 + 𝜎3
2 − 𝜎1 𝜎2 − 𝜎2 𝜎3 − 𝜎3 𝜎1 ≤ 𝑆 𝑦
2

26. Static failure theories
Ductile materials: distortion energy theory
𝑆 𝑦
2 = 𝜎1
2 + 𝜎2
2 + 𝜎3
2 − 𝜎1 𝜎2 − 𝜎2 𝜎3 − 𝜎3 𝜎1
For a 2D stress where 𝜎2= 0, 𝑆 𝑦
2 = 𝜎1
2 + 𝜎3
2 − 𝜎1 𝜎3
• The 2D distortion
energy equation is
described in an ellipse
• The interior of the
ellipse show the biaxial
safe stress sage against
yielding under static
loads

27. Static failure theories
Ductile materials: distortion energy theory
𝑆 𝑦
2 = 𝜎1
2 + 𝜎2
2 + 𝜎3
2 − 𝜎1 𝜎2 − 𝜎2 𝜎3 − 𝜎3 𝜎1
•The 3D distortion
energy equation is
described in cylinder
inclined to principal
stress axes
•The interior of the
cylinder show the
region safe against
yielding for combined
stresses 1, 2, & 3
stress sage under
static loads

28. Static failure theories
Ductile materials: distortion energy theory
𝑆 𝑦
2 = 𝜎1
2 + 𝜎2
2 + 𝜎3
2 − 𝜎1 𝜎2 − 𝜎2 𝜎3 − 𝜎3 𝜎1
Intersection of
the cylinder
with each of
the principal
planes are
ellipses similar
to the 2D
stresses

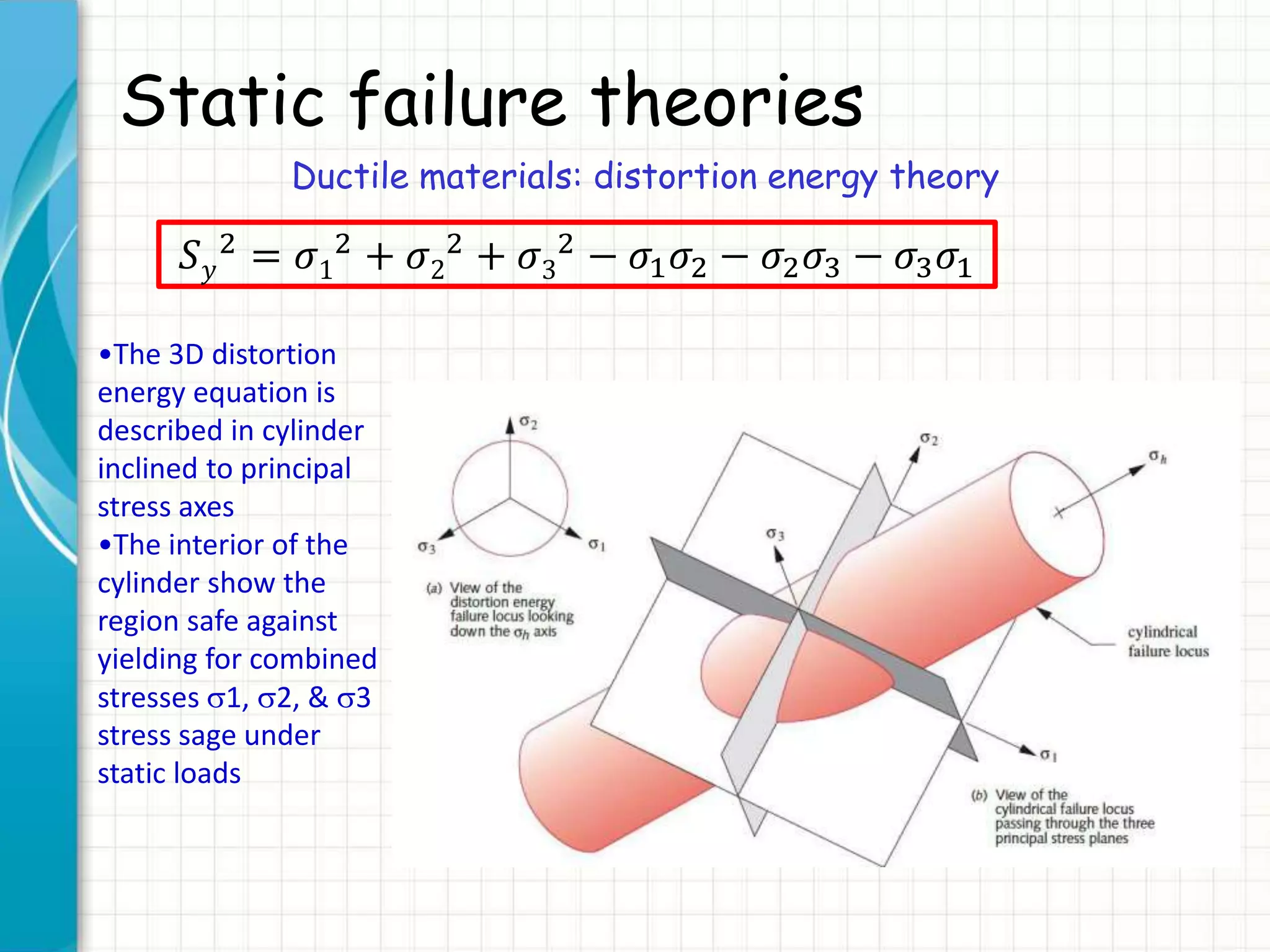
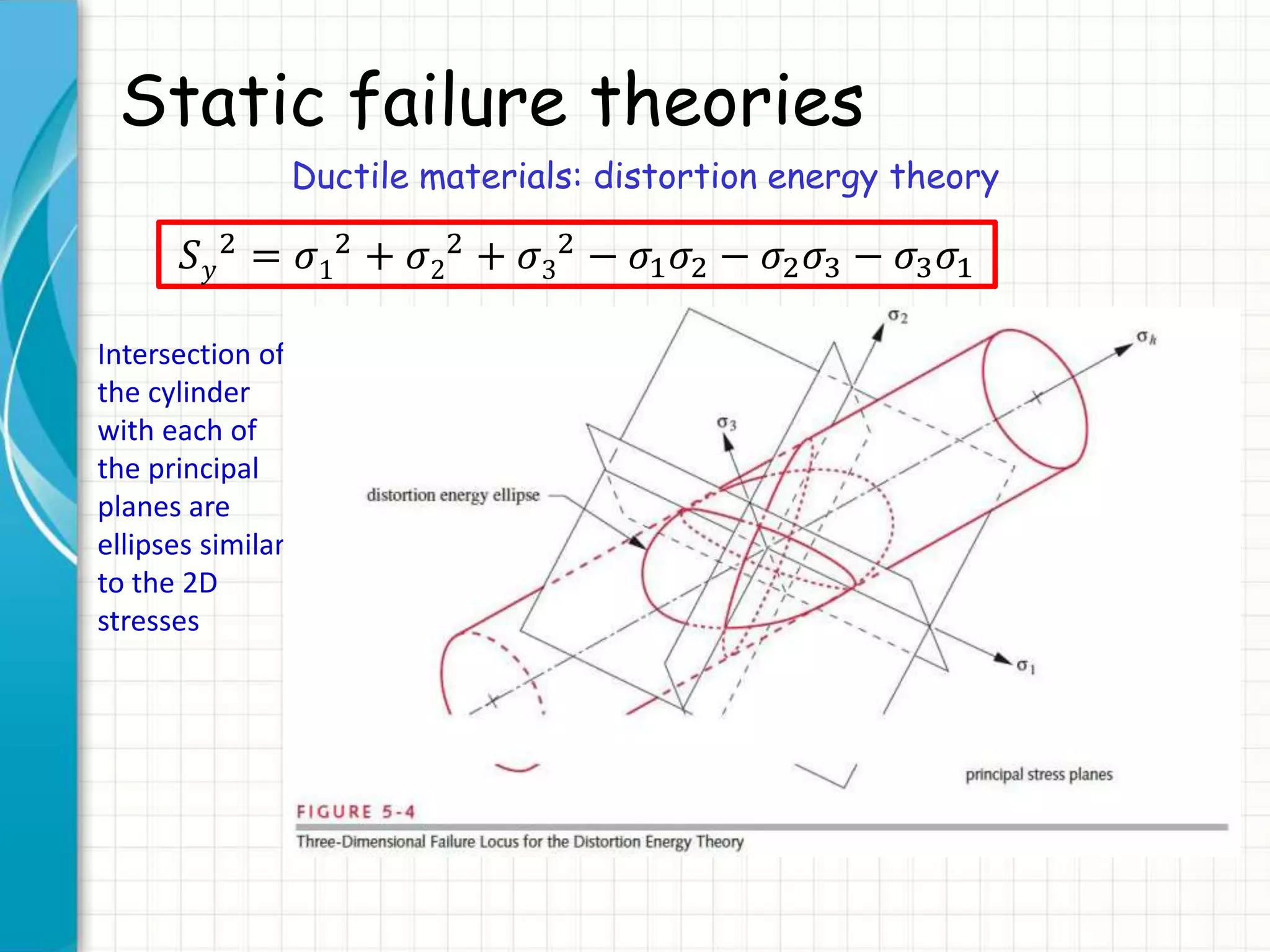
29. Static failure theories
Ductile materials: distortion energy theory
Von Mises effective stress
𝑆 𝑦
2 = [𝜎1
2 + 𝜎2
2 + 𝜎3
2 − 𝜎1 𝜎2 − 𝜎2 𝜎3 − 𝜎3 𝜎1] ≡ 𝜎′ 2
Definition:
𝜎′ = 𝜎1
2
+ 𝜎2
2
+ 𝜎3
2
− 𝜎1 𝜎2 − 𝜎2 𝜎3 − 𝜎3 𝜎1
(Yield surface)
von Mises effective stress
von Mises effective stress: uniaxial stress that would create the
same distortion energy as is created by actual combination of
applied stresses

30. Distortion Energy Theory (DET)
• The failure theory based on distortion
energy is also known as von Mises-Hencky
𝜎′
≤ 𝑆 𝑦
𝑆𝐹 =
𝑆 𝑦
𝜎′
Yield strength of
the material
von Mises
effective
stress

31. Static failure theories
Ductile materials: distortion energy theory
Example: pure shear load
as in case of torsional failure Mohr’s circle:
pure shear𝜎1= max : 𝜎3 =- max and 𝜎2 = 0
𝑆 𝑦
2
= 𝜎1
2
+ 𝜎2
2
+ 𝜎3
2
− 𝜎1 𝜎2
− 𝜎2 𝜎3 − 𝜎3 𝜎1
Using:
𝑆 𝑦
2 = 3𝜏2
𝑚𝑎𝑥
𝑆 𝑦𝑠 ≡ 𝜏 𝑚𝑎𝑥 =
1
3
𝑆 𝑦 = 0.577𝑆 𝑦
Maximum stress before failure, in this case, is: 𝑆 𝑦𝑠 =
1
3
𝑆 𝑦 = 0.577𝑆 𝑦

32. Static failure theories: experimental verifications
Ductile & brittle materials

33. Applicable examples
• A circular rod is subjected to combined
loading consisting of a tensile load P = 10
kN and a torque T = 5 kN-m. Rod is 50 mm
in diameter.
– 1) Draw stress element (cube) at the most highly
stressed location on the rod, and
– 2) draw corresponding Mohr’s circle(s).

35. Example: Failure of ductile material under
static loading
Problem: Determine the safety factors for the bracket rod based on
the both the distortion-energy theory and the maximum shear
theory and compare
Given: Yield strength Sy=324 MPa Rod length L=150 mm
Arm length a=200 mm Rod diameter d=38 mm
Load F=4450 N

36. • Limiting to bending of cantilever and in
torsion
• The shear and moment diagrams will be
similar to a cantilever beam loaded at its end