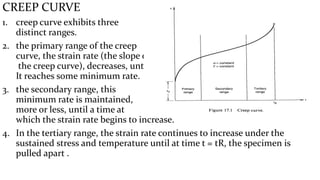
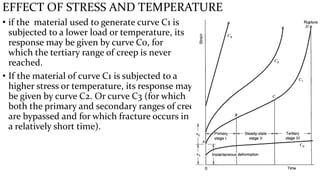
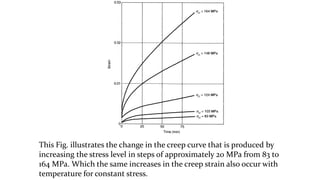
Creep is defined as time-dependent inelastic strain under sustained load and elevated temperature. Creep testing involves subjecting metal specimens to high stress and temperature to produce time-dependent inelastic strain. The creep curve exhibits three stages: primary, secondary, and tertiary. Creep is affected by stress, temperature, and time based on empirical formulas. Creep behavior is more complex for nonmetals like concrete and wood due to additional factors like aging, moisture content, and anisotropy. Creep testing and modeling helps understand material deformation over long periods under load.

1. CREEP
PREPARED BY
MOHAMMED AMER KAMIL

2. Introduction
• creep being defined as time-dependent inelastic strain under sustained
load and elevated temperature.
• the meaning of elevated temperature must be determined individually
for each material on the basis of its behavior, for example, at 205°C
(400°F) for aluminum alloys, 315°C (600°F) for titanium alloys, 370°C
(700°F) for low-alloy steels.
• for certain plastics, asphalt, concrete, lead, and lead alloys, elevated
temperatures for creep behavior may lie in the range of "ordinary
temperatures," say, from 0°C to 50°C (32°F to 122°F).

3. THE TENSION CREEP TEST FOR METALS
1. Various standards for creep testing specify
the geometric design of test specimens
(ASTM, 1983; BSI, 1987; ISO, 1987).
2. During the test, the tension specimen is
subjected to sufficiently high stress a and
temperature T to produce time-dependent
inelastic strain (creep).
3. the strain in the specimen varies with time.
For an appropriate constant stress and
elevated temperature.
4. a strain-time plot (creep curve)

4. CREEP CURVE
1. creep curve exhibits three
distinct ranges.
2. the primary range of the creep
curve, the strain rate (the slope of
the creep curve), decreases, until
It reaches some minimum rate.
3. the secondary range, this
minimum rate is maintained,
more or less, until a time at
which the strain rate begins to increase.
4. In the tertiary range, the strain rate continues to increase under the
sustained stress and temperature until at time t = tR, the specimen is
pulled apart .

5. EFFECT OF STRESS AND TEMPERATURE
• if the material used to generate curve C1 is
subjected to a lower load or temperature, its
response may be given by curve C0, for
which the tertiary range of creep is never
reached.
• If the material of curve C1 is subjected to a
higher stress or temperature, its response may
be given by curve C2. Or curve C3 (for which
both the primary and secondary ranges of creep
are bypassed and for which fracture occurs in
a relatively short time).

6. This Fig. illustrates the change in the creep curve that is produced by
increasing the stress level in steps of approximately 20 MPa from 83 to
164 MPa. Which the same increases in the creep strain also occur with
temperature for constant stress.

7. Creep formulas for metals
• A number of formulas that have been used to represent creep curves.
• the equations separated into time-, temperature-, and stress-dependent
parts.
• The time- dependence formulas are sometimes of the form
ϵ=ϵ0+ϵ 𝑐
where ϵ 𝑐= ϵ 𝑃𝐶 + ϵ 𝑆𝐶 + ϵ 𝑇𝐶, ϵ is the total strain, ϵ0 is the instantaneous strain,
ϵ 𝑐 is creep strain, and ϵ 𝑃𝐶, ϵ 𝑆𝐶, ϵ 𝑇𝐶denote primary, secondary, and tertiary
creep, respectively.

9. • The temperature dependency of creep is often related to thermodynamics and rate processes of solid-state
physics, the temperature dependency is often of exponential form.

10. ϵ denotes total strain, ϵ 𝑐 creep strain, σ stress, T temperature, t time, ln the natural logarithm, exp
the exponential e, and a, b, c,..., A, B, C,... parameters that may be functions of σ, t, T or they may be
constants. Time derivative is denoted by a dot over a symbol (e.g.,∈ 𝑜). The notation f(x) denotes a
function of x.

11. Creep of nonmetals
• the mechanical behavior of many nonmetallic materials during creep is
somewhat simpler than that of metals like glass, polymers, and cements .
• The creep behavior of other nonmetals, such as concrete, asphalt, and wood,
is very complex.
• Concrete is a material that undergoes an aging process, such that under
sustained load the modulus of elasticity changes with time.
• Aging is a phenomenon that alters creep of concrete. It is caused mainly by
cement hydration, a process that continues for a long time after the initial
hardening period. Aging changes the rate of creep and, hence, must be
accounted for. This fact increases the difficulty of predicting the creep
behavior of concrete.

12. The creep of asphalt
• that asphalt possesses elastic, viscous, and plastic properties dependent on
the temperature and duration of loads.
• At low temperatures and for short duration of load, asphalt behaves in an
almost linear elastic manner.
• At high temperatures and long duration of loads, asphalt responds in a
viscous manner.
• Asphalt responds plastically at high levels of loads or under localized high
stress .
• The relation of creep to the engineering properties of asphalt (e.g., rutting of
pavements, total deformation, strength, etc.)

13. Calculating the creep of asphalt
for conducting uniaxial static creep tests with asphalt test specimens and
recommends the logarithmic flow rule :
ϵ = A + В log t
where A and В are material constants determined by the tests. a relatively low
value of В indicates low viscous behavior; a high value of В suggests mainly
viscous behavior.

14. The creep of concrete
• The creep of concrete is affected by a large number of factors. For example,
water-reducing admixtures tend to increase creep rates.
• Many other experimental variables affect the creep of concrete, for example,
paste parameters (porosity, age, etc.), concrete parameters (aggregate
stiffness, aggregate/cement content, volume to surface ratio), and
environmental parameters (applied stress, duration of load, humidity, etc.).
• Usually, the creep of concrete is influenced more by paste properties, since
the aggregate tends to retard creep rate.

15. Calculating creep of concrete
the creep strain-stress relation in concrete is commonly taken to be
ϵ 𝑐= фσ
where ф is called the specific creep. The concept of specific creep is useful for
comparing the creep of different concrete specimens at different stress levels. A
typical value of ф is approximately 150 μ /MPa, μ = 10−6 .
Later the American Concrete Institute (ACI, 1991) has developed a simplified creep
equation of the form :
where t denotes time, В is a constant that depends on the age of the concrete
before loading (B is taken to be 10 when the concrete is more than 7 days old before
loading), and Cult is the ultimate creep coefficient. The value of Cult is difficult to
determine, as it may vary considerably (for 40% relative humidity Cult may range
between 1.30 and 4.5). ACI recommends a value of Cult = 2.35.

16. The creep of wood
• the magnitude of creep strain depends on a large number of factors. The
most critical conditions include the alignment of the orthotropic axes of
wood relative to the load, the magnitude and type of stress, the rate of load,
the duration of load, moisture content, and temperature.
• In spite of the complexity of wood, many of the same concepts employed in
the study of creep in metals are used, and the study of creep in wood rests
heavily on curve-fitting of experimental data to obtain approximate flow
rules.

17. Calculating creep of wood
In contrast to creep models of metals that are described in terms of three
stages of creep, the total creep deformation to consist of elastic and viscoelastic
parts.
For example, consider a tension specimen subjected to an instantaneously
applied load P at time t0 (Fig. shown next slide). The deformation at some
later time t1 is taken to be :
Where ẟe is the instantaneous elastic deformation due to the instantaneous
application of load, ẟde a delayed elastic deformation, and ẟv viscous
component.

19. • Bodig and Jayne 1982, derived creep formulas that are the synthesis of linear
viscoelastic models and experimental data, they derived the strain-time
relation :
Note that the first term is the instantaneous elastic strain, the second term is
the delayed elastic strain, and the third is the viscous strain .

20. Reference
• Arthur P. Boresi, Richard J. Schmidt, Omar M. Sidebottom-
Advanced mechanics of materials-Wiley (1993).

21. Thank you for listening