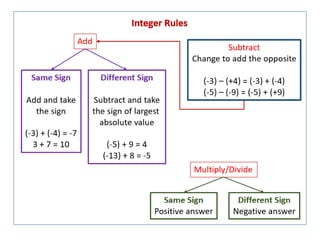
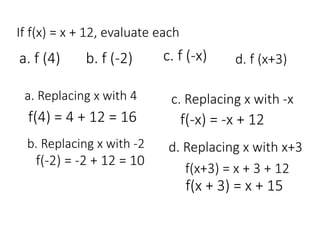This document discusses evaluating functions and operations on functions. It provides examples of evaluating functions at given points by substituting the point value for the variable in the function definition and simplifying. Some key points made include: - Function notation like f(x) identifies the function and indicates the variable it is in terms of - To evaluate a function at a point, substitute the point value for the variable and simplify - Functions can be evaluated using algebraic expressions by substituting the expression for the variable - Examples are provided of evaluating various functions at given points or expressions

1. Evaluating Functions and Operations
on Functions

4. Function Notation
y = x2 – 4 f(x) = x2 – 4
•Pronounced f of x
Identifies the equation as a
function Indicates which variable the
function is in terms of (the
variable used in the function)

7. Evaluating Function
Remember that:
f(x) = 3x +1:
1. f(x) means “the value of f at x”. It does not
mean “f times x.”
2.Letters other than f such as G and H or g
and h can also be used.
3. f is the name of the function and f(x) is the
value of the function at x.

9. 8+(8)= 16
49- (5) 2
49 – 25
24

10. Evaluating Functions Algebraically
•Solve for the value of a function at a
point.
•f(x) = 2x – 10; find f(6)
•f(6) = 2(6) – 10
f(6) = 12 – 10
f(6) = 2
The value of x is 6.
Replace x with 6 and
solve.

11. Function Notation
11
Given g(x) = x2 – 3, find g(-2) .
g(-2) = x2 – 3
g(-2) = (-2)2 – 3
g(-2) = 1

12. Function Notation
12
Given f(x) = , the following.
f(3) = 2x2 – 3x
f(3) = 2(3)2 – 3(3)
f(3) = 2(9) - 9
f(3) = 9
a. f(3) b. 3f(x) c. f(3x)
3f(x) = 3(2x2 – 3x)
3f(x) = 6x2 – 9x
f(3x) = 2x2 – 3x
f(3x) = 2(3x)2 – 3(3x)
f(3x) = 2(9x2) – 3(3x)
f(3x) = 18x2 – 9x
2
2 3
x x


13. If f(x) = x + 12, evaluate each
a. f (4) b. f (-2) c. f (-x) d. f (x+3)
a. Replacing x with 4
f(4) = 4 + 12 = 16
b. Replacing x with -2
f(-2) = -2 + 12 = 10
c. Replacing x with -x
f(-x) = -x + 12
d. Replacing x with x+3
f(x+3) = x + 3 + 12
f(x + 3) = x + 15

14. Evaluating Functions Algebraically,
cont.
•You can also evaluate functions with
an expression
•f(x) = 2x – 10; find f(x+1)
f(x+1) = 2(x+1) – 10
f(x+1) = 2x + 2 – 10
f(x+1) = 2x – 8

15. 6(-5) + 100
-30 + 100
70

16. h(4) = -3(4) -5
h(4) = -12 - 5
h(4) = -17
h(4) = -3x -5
h(-3) = -3(-3) -5
h(-3) = 9- 5
h(-3) = 4
h(-3) = -3x -5

17. f(-1) = (-1)2 +3(-1) -4
f(-1) = 1 – 3 - 4
f(-1) = -6
f(-1) = x2 +3x-4
h(4) = (4)2 +3(4) -4
h(4) = 16 + 12 - 4
h(4) = 24
h(4) = x2 +3x-4

18. EXPONENTS
f(6) = (-12 +6 )2
f(6) = (-12 ) 2 + (6 )2
f(6) = 144 + 36
f(6) = (-12 +x)2
f(6) = 180

19. ACTIVITY TIME

21. INTEGERS
g(-4) = -3 + (-4)
g(-4) = -3 - 4
g(-4) = -7
g(-4) = -3 + x

22. f(-10) = 4 +(-10)
f(-10) = -6

23. f(4) = (−4) + (−2) − 1
f(4) = -6 - 1
f(4) = -7
f(4) = (−4) + (−2) − 4 ÷ 4

24. f(3) = 9 ÷ (3)2 + 2 − 2 (3)
f(3) = 9 ÷ 9+ 2 − 6
f(3) = 1 + 2 - 6
f(3) = 9 ÷ 𝑥2 + 2 − 2 𝑥
f(3) = -3