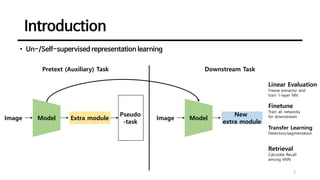
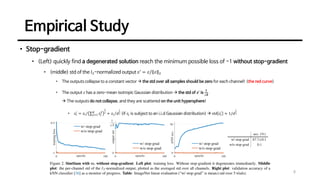
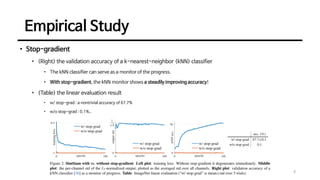
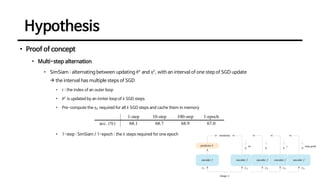
This document discusses an unsupervised representation learning method called SimSiam. It proposes that SimSiam can be interpreted as an expectation-maximization algorithm that alternates between updating the encoder parameters and assigning representations to images. Key aspects discussed include how the stop-gradient operation prevents collapsed representations, the role of the predictor network, effects of batch size and batch normalization, and alternatives to the cosine similarity measure. Empirical results show that SimSiam learns meaningful representations without collapsing, and the various design choices affect performance but not the ability to prevent collapsed representations.

1. Sungchul Kim

2. Contents
1. Introduction
2. Method
3. Empirical Study
4. Comparisons
5. (Hypothesis)
2

3. Introduction
3
• Un-/Self-supervised representation learning
Pretext (Auxiliary) Task
Image Model Extra module
Pseudo
-task
Downstream Task
Image Model
New
extra module
Linear Evaluation
Freeze extractor and
train 1-layer NN
Finetune
Train all networks
for downstream
Transfer Learning
Detection/segmentation
Retrieval
Calculate Recall
among kNN

4. Introduction
4
• Siamese networks
• An undesired trivial solution : all outputs “collapsing” to a constant
• Constrastive Learning
• Attract the positive sample pairs and repulse the negative sample pairs
• SimCLR, MoCo, …
• Clustering
• Alternate between clustering the representations and learning to predict the cluster assignment
• SwAV
• BYOL
• A Siamese network in which one branch is a momentum encoder

5. Introduction
5
• SimSiam
• Without the momentum encoder, negative pairs, and online clustering
• Does not cause collapsing and can perform competitively
• Siamese networks : inductive biases for modeling invariance
• Invariance : two observations of the same concept should produce the same outputs.
• The weight-sharing Siamese networks can model invariance w.r.t. more complicated transformations
(augmentations).

6. Method
6
• SimSiam
• Two randomly augmented views 𝑥1 and 𝑥2 from an image 𝑥
• An encoder network 𝑓 consisting of a backbone and a projection MLP head
• Two output vectors 𝑝1 ≜ ℎ 𝑓 𝑥1 and 𝑧2 ≜ 𝑓 𝑥2
𝒟 𝑝1, 𝑧2 = −
𝑝1
𝑝1 2
⋅
𝑧2
𝑧2 2
• A symmetrized loss
ℒ =
1
2
𝒟 𝑝1, 𝑧2 +
1
2
𝒟 𝑝2, 𝑧1
• Stop-gradient operation
ℒ =
1
2
𝒟 𝑝1, stopgrad 𝑧2 +
1
2
𝒟 𝑝2, stopgrad 𝑧1

7. Method
7
• SimSiam
• Baseline Settings
• Optimizer
• SGD with 0.9 momentum and weight decay 0.0001
• Learning rate : 𝑙𝑟 × BatchSize/256 with a base 𝑙𝑟 = 0.05
• Batch size : 512 / Batch normalization synchronized across devices
• Projection MLP
• (FC (2048) + BN + ReLU) x 2 + FC (𝑑=2048) + BN (𝑧)
• Prediction MLP
• FC (512)+ BN + ReLU + FC (𝑑=2048) (𝑝)
• Experimental setup
• Pre-training : 1000-class ImageNet training set
• Linear evaluation : training a supervised linear classifier on frozen representations

8. Empirical Study
8
• Stop-gradient
• (Left) quickly find a degenerated solution reach the minimum possible loss of -1 without stop-gradient
• (middle) std of the 𝑙2-normalized output z′
= 𝑧/ 𝑧 2
• The outputs collapse to a constant vector → the std over all samples should be zero for each channel! (the red curve)
• The output 𝑧 has a zero-mean isotropic Gaussian distribution → the std of 𝒛′ is
𝟏
𝒅
→ The outputs do not collapse, and they are scattered on the unit hypersphere!
• 𝑧𝑖
′
= Τ
𝑧𝑖 σ𝑗=1
𝑑
𝑧𝑗
2
1
2
≈ Τ
𝑧𝑖 𝑑
1
2 (if 𝑧𝑗 is subject to an i.i.d Gaussian distribution) → std 𝑧𝑖
′
≈ 1/𝑑
1
2

9. Empirical Study
9
• Stop-gradient
• (Right) the validation accuracy of a k-nearest-neighbor (kNN) classifier
• The kNN classifier can serve as a monitor of the progress.
• With stop-gradient, the kNN monitor shows a steadily improving accuracy!
• (Table) the linear evaluation result
• w/ stop-grad : a nontrivial accuracy of 67.7%
• w/o stop-grad : 0.1%..

10. Empirical Study
10
• Stop-gradient
• Discussion
• There exist collapsing solutions.
• The minimum possible loss and the constant outputs (Of course, it is not sufficient to indicate collapsing!)
• It is insufficient for our method to prevent collapsing solely by the architecture designs (e.g., predictor, BN, 𝑙2-norm).

11. Empirical Study
11
• Predictor
• (Table 1) the predictor MLP (ℎ)’s effect
• (a) removing ℎ (=ℎ is the identity mapping) → the model does not work!
• ℒ(a) =
1
2
𝒟 𝑧1, stopgrad 𝑧2 +
1
2
𝒟 𝑧2, stopgrad 𝑧1
• Same direction as the gradient of 𝒟 𝑧1, 𝑧2 with the magnitude scaled by 1/2 → collapsing!
• The asymmetric variant 𝒟 𝑝1, stopgrad 𝑧2 also fails if removing ℎ, while it can work if ℎ is kept.

12. Empirical Study
12
• Predictor
• (Table 1) the predictor MLP (ℎ)’s effect
• (b) ℎ is fixed as random initialization → the model does not work!
• This failure is not about collapsing. The training does not converge, and the loss remains high.
• (c) ℎ with a constant 𝑙𝑟 (without decay) → works well!
• It is not necessary to force it converge (by reducing 𝑙𝑟) before the representations are sufficiently trained.

13. Empirical Study
13
• Batch Size
• (Table 2) the results with a batch size from 64 to 4096
• Linear scaling rule (𝑙𝑟 × BatchSize/256) with base 𝑙𝑟 = 0.5
• 10 epochs of warm-up for batch sizes ≥ 1024
• SGD optimizer, not LARS
• 64, 128 : a drop of 0.8% or 2.0% in accuracy
• 256 to 2048 : similarly good
→ SimSiam, SimCLR, SwAV : Siamese network with direct weight-sharing
→ SimCLR and SwAV both require a large batch (e.g., 4096) to work well.
→ The standard SGD optimizer does not work well when the batch is too large.
→ A specialized optimizer is not necessary for preventing collapsing.

14. Empirical Study
14
• Batch Normalization
• (Table 3) the configurations of BN on the MLP heads
• (a) remove all BN layers in the MLP heads
• This variant does not cause collapse, although the acc is low (34.6%).
• (b) adding BN to the hidden layers
• It increases accuracy to 67.4%.
• (c) adding BN to the output of the projection MLP (default)
• It boosts accuracy to 68.1%.
• Disabling learnable affine transformation (scale and offset) in 𝑓’s output BN : 68.2%
• (d) adding BN to the output of the prediction MLP ℎ → does not work well!
• Not about collapsing, the training is unstable and the loss oscillates.
→ BN is helpful for optimization when used appropriately.
→ No evidence that BN helps to prevent collapsing.

15. Empirical Study
15
• Similarity Function
• Modify 𝒟 as: 𝒟 𝑝1, 𝑧2 = −softmax 𝑧2 ⋅ log softmax 𝑝1
• The output of softmax can be thought of as the probabilities of belonging to each of 𝑑 pseudo-categories.
• Simply replace the cosine similarity with the cross-entropy similarity, and symmetrize it.
• The cross-entropy variant can converge to a reasonable result without collapsing.
→ The collapsing prevention behavior is not just about the cosine similarity.

16. Empirical Study
16
• Symmetrization
• Observe that SimSiam’s behavior of preventing collapsing does not depend on symmetrization.
• Compare with the asymmetric variant (𝒟 𝑝1, stopgrad 𝑧2 ).
• The asymmetric variant achieves reasonable results.
→ Symmetrization is helpful for boosting accuracy, but it is not related to collapse prevention.
• Sampling two pairs for each image in the asymmetric version (“2x”)
→ It makes the gap smaller.

17. Empirical Study
17
• Summary
• SimSiam can produce meaningful results without collapsing.
• The optimizer (batch size), batch normalization, similarity function, and symmetrization
→ affect accuracy, but we have seen no evidence about collapsing prevention
→ the stop-gradient operation may play an essential role!

18. Hypothesis
18
• What is implicitly optimized by SimSiam?
• Formulation
• SimSiam is an implementation of an Expectation-Maximization (EM) like algorithm.
ℒ 𝜃, 𝜂 = 𝔼𝑥,𝒯 ℱ𝜃 𝒯 𝑥 − 𝜂𝑥 2
2
• ℱ : a network parameterized by 𝜃
• 𝒯 : the augmentation / 𝑥 : an image
• 𝜂 : another set of variables (proportional to the number of images)
• 𝜂𝑥 : the representation of the image 𝑥 / the subscript 𝑥 : using the image index to access a sub-vector of 𝜂
• The expectation 𝔼 ⋅ is over the distribution of images and augmentations.
• The mean squared error ⋅ 2
2
: equivalent to the cosine similarity if the vectors are 𝑙2-normalized

19. Hypothesis
19
• Formulation
• Solve min
𝜃,𝜂
ℒ 𝜃, 𝜂
• This formulation is analogous to k-means clustering.
• The variable 𝜃 is analogous to the clustering centers (the learnable parameters of an encoder)
• The variable 𝜂𝑥 is analogous to the assignment vector of the sample 𝑥 (a one-hot vector, the representation of 𝑥)
• An alternating algorithm
• Solving for 𝜽 (𝜃𝑡
← argmin𝜃ℒ 𝜃, 𝜂𝑡−1
)
• The stop-gradient operation is a natural consequence
: the gradient does not back-propagate to 𝜂𝑡−1
which is a constant.
• Solving for 𝜼 (𝜂𝑡
← argmin𝜂ℒ 𝜃𝑡
, 𝜂 )
• Minimize 𝔼𝒯 ℱ𝜃𝑡 𝒯 𝑥 − 𝜂𝑥 2
2
for each image 𝑥 : 𝜂𝑥
𝑡
← 𝔼𝒯 ℱ𝜃𝑡 𝒯 𝑥 (due to the mean squared error)
• 𝜂𝑥 is assigned with the average representation of 𝑥 over the distribution of augmentation.

20. Hypothesis
20
• Formulation
• One-step alternation
• Approximate 𝜂𝑥
𝑡
← 𝔼𝒯 ℱ𝜃𝑡 𝒯 𝑥 by sampling the augmentation only once (𝒯′) and ignoring 𝔼𝒯 ⋅
𝜂𝑥
𝑡
← ℱ𝜃𝑡 𝒯′
𝑥
• Then,
𝜃𝑡+1
← argmin𝜃𝔼𝑥,𝒯 ℱ𝜃 𝒯 𝑥 − ℱ𝜃𝑡 𝒯′
𝑥 2
2
• 𝜃𝑡
: a constant in this sub-problem
• 𝒯′ : another view due to its random nature
→ The SimSiam algorithm: a Siamese network naturally with stop-gradient applied.

21. Hypothesis
21
• Formulation
• Predictor
• Assume : ℎ is helpful in our method because of the approximation ~.
• Minimize 𝔼𝑧 ℎ 𝑧1 − 𝑧2 2
2
→ the optimal solution : ℎ 𝑧1 = 𝔼𝑧 𝑧2 = 𝔼𝒯 𝑓 𝒯 𝑥 for any image 𝑥
• In practice, it would be unrealistic to actually compute the expectation 𝔼𝒯
• But it may be possible for a neural network (e.g., the predictor ℎ) to learn to predict the expectation,
while the sampling of 𝒯 is implicitly distributed across multiple epochs.
• Symmetrization
• Symmetrization is like denser sampling 𝒯.
• 𝔼𝑥,𝒯 ⋅ by sampling a batch of images and one pair of augmentation 𝒯
1, 𝒯
2
• Symmetrization supplies an extra pair 𝒯
2, 𝒯
1
• Not necessary, yet improving accuracy

22. Hypothesis
22
• Proof of concept
• Multi-step alternation
• SimSiam : alternating between updating 𝜃𝑡
and 𝜂𝑡
, with an interval of one step of SGD update
→ the interval has multiple steps of SGD
• 𝑡 : the index of an outer loop
• 𝜃𝑡
is updated by an innter loop of 𝑘 SGD steps
• Pre-compute the 𝜂𝑥 required for all 𝑘 SGD steps and cache them in memory
• 1-step : SimSiam / 1-epoch : the 𝑘 steps required for one epoch

23. Hypothesis
23
• Proof of concept
• Expectation over augmentations
• Do not update 𝜂𝑥 directly, maintain a moving-average
𝜂𝑥
𝑡
← 𝑚 ∗ 𝜂𝑥
𝑡−1
+ 1 − 𝑚 ∗ ℱ𝜃𝑡 𝒯′
𝑥 𝑚 = 0.8
• This moving-average provides an approximated expectation of multiple views.
• 55.0% accuracy without the predictor ℎ
• Fails completely if removing ℎ but do not maintain the moving average. (Table 1a)
→ The usage of predictor ℎ is related to approximating 𝔼𝒯 ⋅
• Discussion
• It does not explain why collapsing is prevented.

24. Comparisons
24
• Result Comparisons
• ImageNet
• SimSiam achieves competitive results with its simplicity.
• The highest accuracy among all methods under 100-epoch pre-training
• Better results than SimCLR in all cases

25. Comparisons
25
• Result Comparisons
• Transfer Learning
• VOC (object detection) and COCO (object detection and instance segmentation)
• SimSiam, base : the baseline pre-training recipe
• SimSiam, optimal : optimal recipe (𝑙𝑟=0.5 and 𝑤𝑑=1e-5)
• Siamese structure is a core factor for their general success.

26. Comparisons
26
• Methodology Comparisons
• Relation to SimCLR
• SimSiam is SimCLR without negatives.
• Negative samples (“dissimilarity”) to prevent collapsing
• Append the prediction MLP ℎ and stop-gradient to SimCLR
• Neither the stop-gradient nor the extra predictor is necessary or helpful.
• a consequence of another underlying optimization problem.
• It is different from the contrastive learning problem!
• Relation to BYOL
• SimSiam is BYOL without the momentum encoder.
• The momentum encoder may be beneficial for accuracy, but it is not necessary for preventing collapsing.

27. 감 사 합 니 다
27