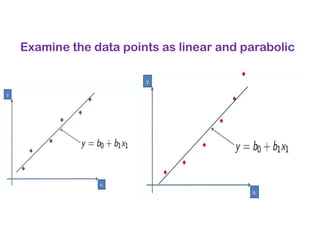
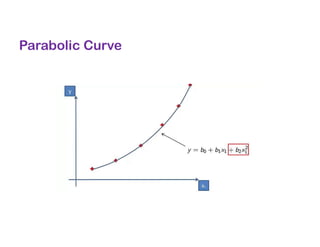
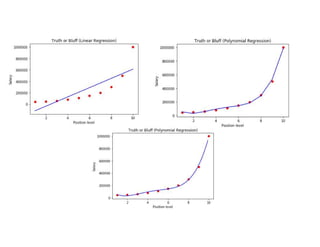
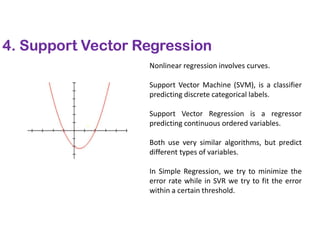
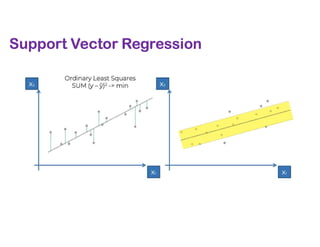
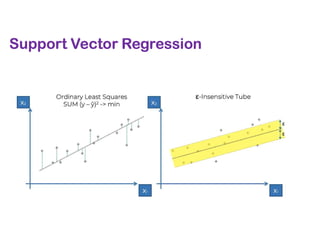
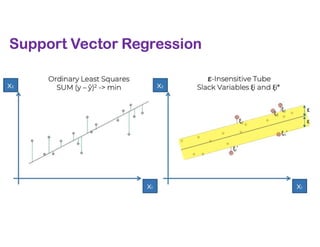
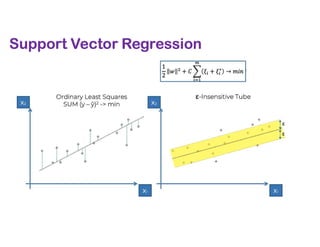
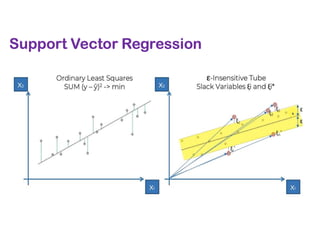
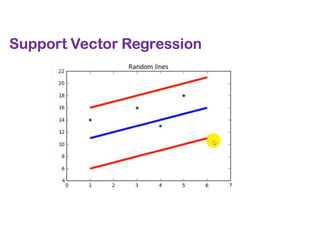
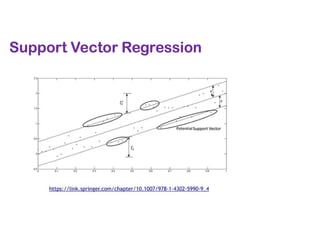
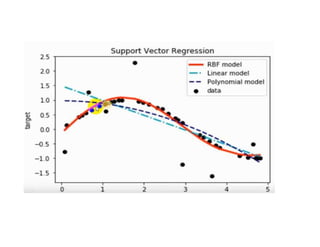
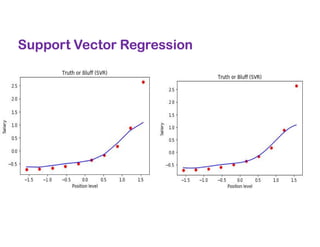
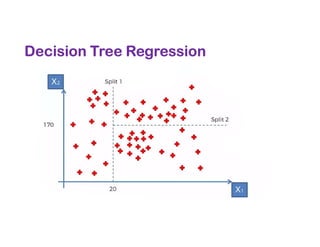
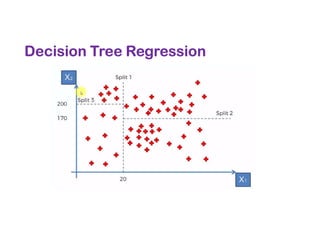
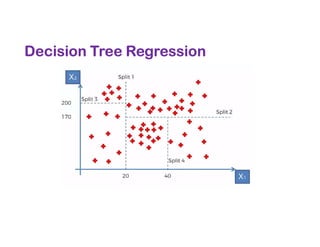
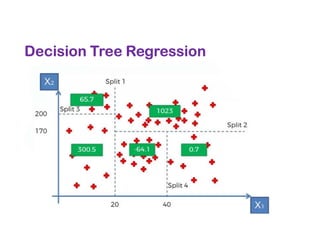
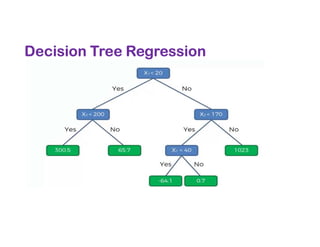
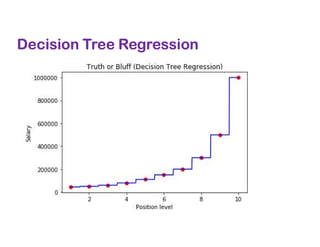
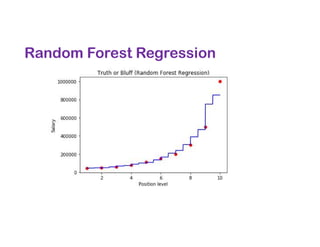
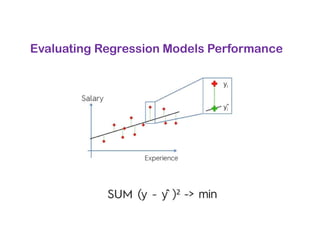
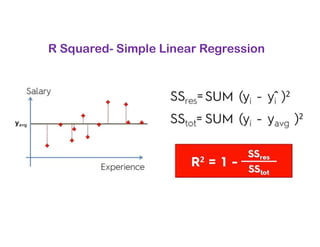
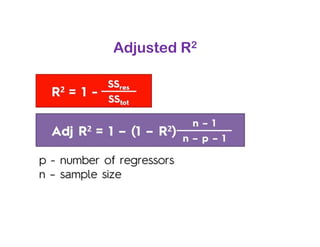
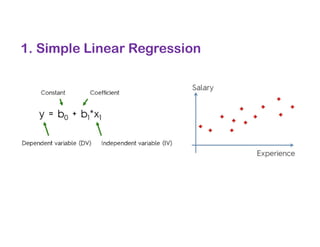
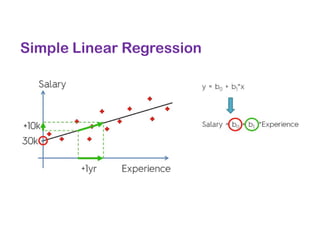
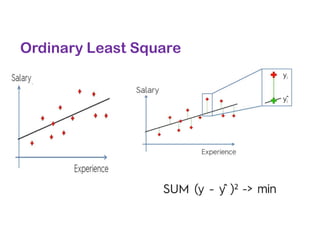
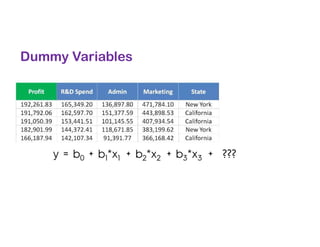
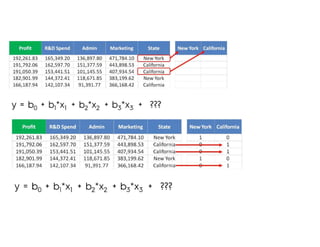
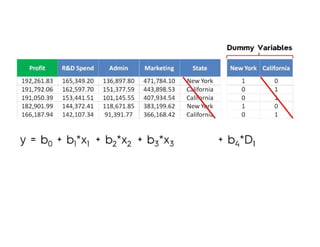
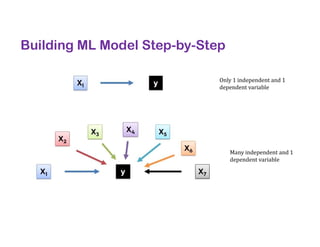
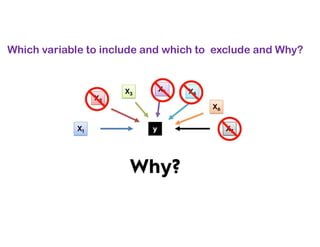
The document covers various regression techniques including simple linear regression, multiple linear regression, polynomial regression, support vector regression, decision tree regression, and random forest regression. It elaborates on the building of machine learning models, variable selection methods, and provides sample Python code for implementing multiple linear regression. Additionally, it includes details on evaluating regression models and interpreting coefficients.

1. Regression

2. Linear Regression
• Simple Linear Regression
• Multiple Linear Regression
• Polynomial Regression
Non-Linear Regression
• Support Vector Regression (SVR)
• Decision Tree Regression
• Random Forest Regression

3. 1. Simple Linear Regression

4. Simple Linear Regression

5. Ordinary Least Square

6. 2. Multiple Linear Regression

7. A Caveat

8. Dummy Variables

11. Dummy Variable Trap

12. Statistical Significance

13. Tossing a coin
H0: Fair Coin
H1: Unfair Coin
0.5
0.25
0.12
0.06
0.03
0.01
P-Value
α = 0.05

14. P-Value (Probability Value)

15. Building ML Model Step-by-Step
Only 1 independent and 1
dependent variable
Many independent and 1
dependent variable

16. Which variable to include and which to exclude and Why?

17. Selecting the Right Variable

18. 5 Methods of Building Models
1.All-in
2.Backward Elimination
3.Forward Selection
4.Bidirectional Elimination
Stepwise
Regression

19. All-in Model
Include all the variables in the model when:
• You have prior knowledge because of domain knowledge or such similar model has
been done previously.
• You have to because of some existing framework in the organization etc.

20. Backward Elimination

21. Backward Elimination

22. Forward Elimination

23. Bidirectional Elimination

24. All Possible Models

25. Multiple Regression- Python Code
# Importing the libraries
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
# Importing the dataset
dataset = pd.read_csv('50_Startups.csv')
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].values
# Encoding categorical data
from sklearn.preprocessing import LabelEncoder, OneHotEncoder
labelencoder = LabelEncoder()
X[:, 3] = labelencoder.fit_transform(X[:, 3])
onehotencoder = OneHotEncoder(categorical_features = [3])
X = onehotencoder.fit_transform(X).toarray()

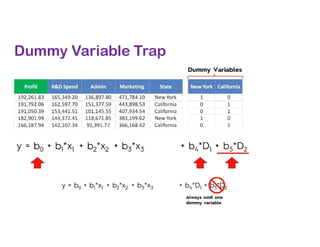
26. # Avoiding the Dummy Variable Trap
X = X[:, 1:]
# Splitting the dataset into the Training set and Test set
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2,
random_state = 0)
# Fitting Multiple Linear Regression to the Training set
from sklearn.linear_model import LinearRegression
regressor = LinearRegression()
regressor.fit(X_train, y_train)
# Predicting the Test set results
y_pred = regressor.predict(X_test)

27. Backward Elimination
# Building an optimal model using Backward Elimination
import statsmodels.regression.linear_model as sm
X = np.append(arr = np.ones((50,1)).astype(int),values = X, axis = 1)
X_opt = X[:,[0,1,2,3,4,5]]
regressor_OLS = sm.OLS(endog = y, exog = X_opt).fit()
regressor_OLS.summary()
X_opt = X[:,[0,3,4,5]]
regressor_OLS = sm.OLS(endog = y, exog = X_opt).fit()
regressor_OLS.summary()

28. 3. Polynomial Linear Regression

29. Examine the data points as linear and parabolic

30. Parabolic Curve

32. 4. Support Vector Regression
Nonlinear regression involves curves.
Support Vector Machine (SVM), is a classifier
predicting discrete categorical labels.
Support Vector Regression is a regressor
predicting continuous ordered variables.
Both use very similar algorithms, but predict
different types of variables.
In Simple Regression, we try to minimize the
error rate while in SVR we try to fit the error
within a certain threshold.

33. Support Vector Regression

34. Support Vector Regression

35. Support Vector Regression

36. Support Vector Regression

37. Support Vector Regression

38. Support Vector Regression
• Kernel : The function used to map a lower dimensional data into a higher
dimensional data.
• Hyper Plane: In SVM this is basically the separation line between the data
classes. Although in SVR we are going to define it as the line that will help
us predict the continuous value or target value.
• Boundary Line: In SVM, there are two lines other than Hyper Plane which
creates a margin. The support vectors can be on the Boundary lines or
outside it. This boundary line separates the two classes. In SVR the concept
is same.
• Support Vectors: This are the data points which are closest to the
boundary. The distance of the points is minimum or least.

39. Support Vector Regression

40. Support Vector Regression

41. Support Vector Regression

43. Support Vector Regression

44. Support Vector Regression

45. Support Vector Regression

46. Support Vector Regression

47. Support Vector Regression

48. 5. Decision Tree Regression

49. Decision Tree Regression

50. Decision Tree Regression

51. Decision Tree Regression

52. Decision Tree Regression

53. Decision Tree Regression

54. Decision Tree Regression

55. Decision Tree Regression

56. Decision Tree Regression

57. 6. Random Forest Regression

58. Random Forest Regression

59. Random Forest Regression

60. Evaluating Regression Models Performance

61. R Squared- Simple Linear Regression

62. Adjusted R2

63. Adjusted R2

64. Interpreting Linear Regression Coefficients

65. Interpreting Linear Regression Coefficients

66. Regression Model Pros and Cons