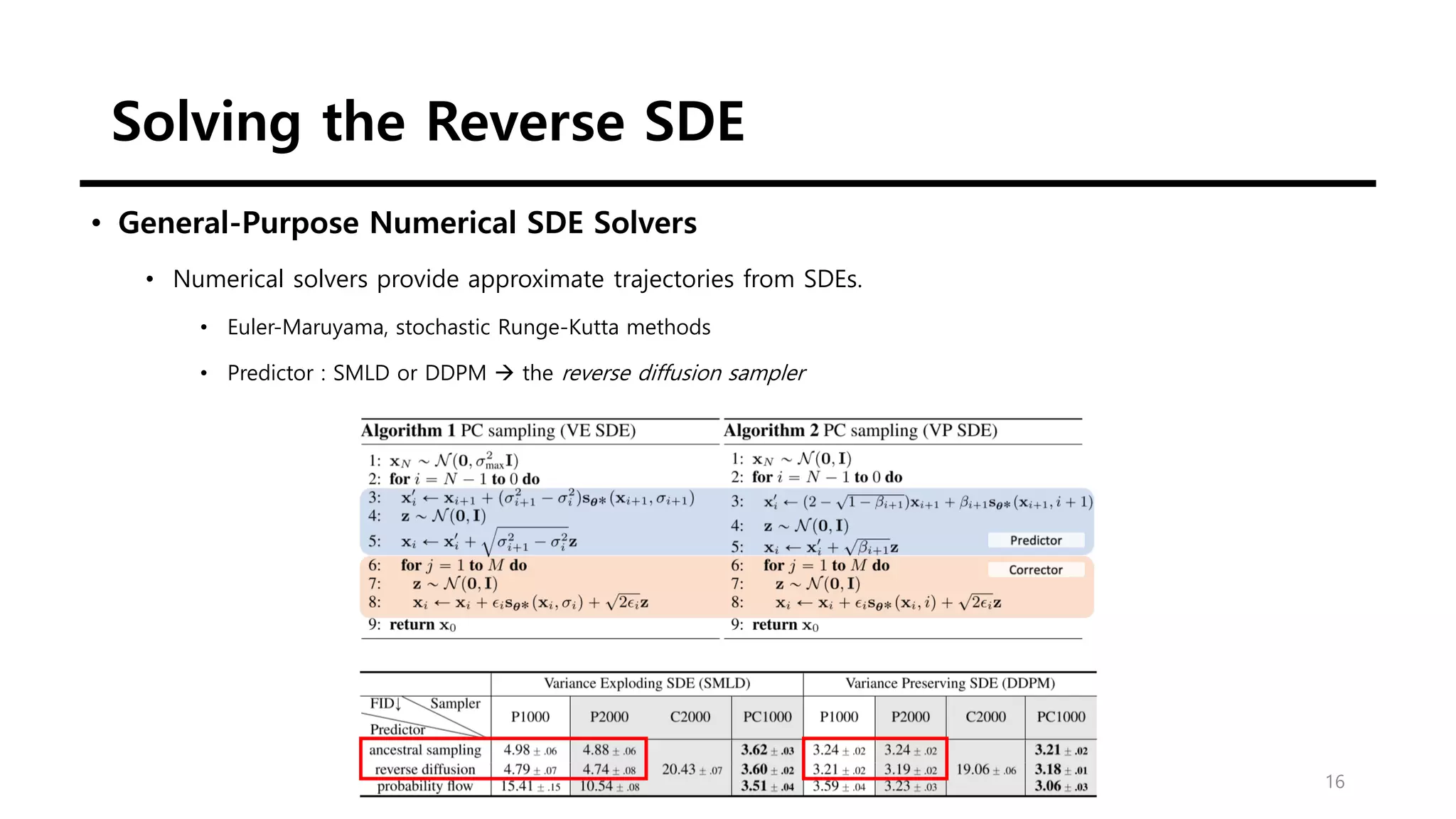
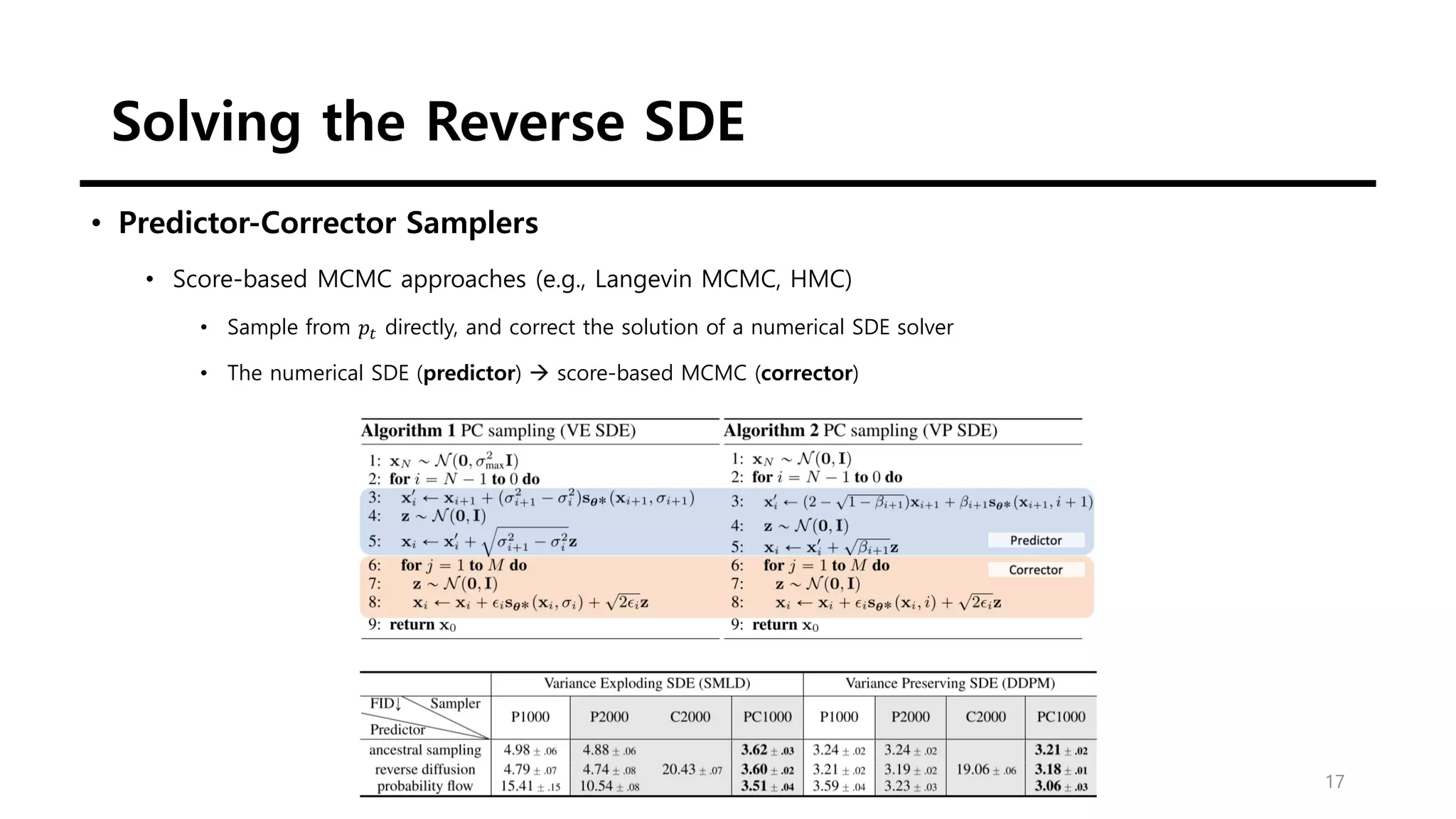
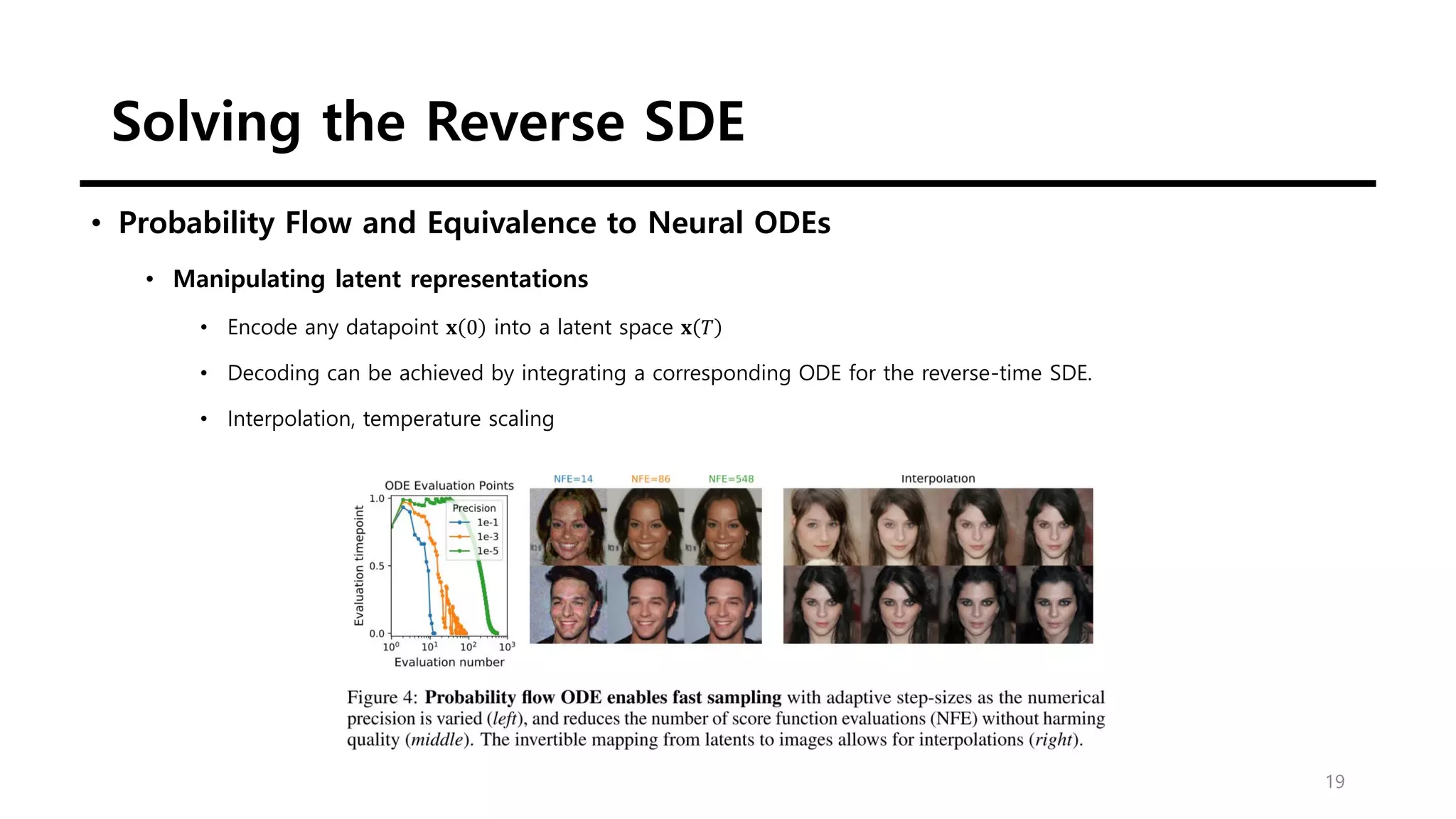
This document discusses score-based generative modeling using stochastic differential equations (SDEs). It introduces modeling data diffusion as an SDE from the data distribution to a simple prior and generating samples by reversing this diffusion process. It also describes estimating the score (gradient of the log probability density) needed for the reverse process using score matching. Finally, it notes that noise perturbation models like NCSN and DDPM can be viewed as discretizations of specific SDEs called variance exploding and variance preserving SDEs.

1. Sungchul Kim

2. Contents
1. Introduction
2. Background
3. Score-based generative modeling with SDEs
4. Solving the Reverse SDE
5. Controllable Generation
6. Discussion
2

3. Introduction
3
• Probabilistic generative models
• Slowly increasing noise / removing noise
• Score matching with Langevin dynamics (SMLD)
• 각 noise scale에서 score (i.e., the gradient of the log probability density, ∇𝐱log 𝑝𝑡 𝐱 ) 계산
• Noise scale 감소에 따른 샘플에 Langevin dynamics 적용
• Denoising diffusion probabilistic modeling (DDPM)
• Noise corruption을 거꾸로 하면서 학습
• 추적가능한 reverse distribution 사용
→ score-based generative models
• The practical performance of these two model classes is often quite different for reasons
that are not fully understood.

4. Introduction
4
• Stochastic Differential Equations (SDEs)
• 유한한 noise distribution으로 perturbing하는 대신,
diffusion하는 방식으로 시간이 지남에 따라 변화하는 a continuum of distributions 고려
• Data → random noise로 diffusion : SDE로 표현
• Random noise → data로 sample generation : a reverse-time SDE

5. Introduction
5
• Contributions
• Flexible sampling
• Reverse-time SDE를 위한 general-purpose SDE
• Predictor-Corrector (PC) : score-based MCMC로 numerical SDE solvers를 결합
• Deterministic samplers : the probability flow ordinary differential equations (ODE)
• Controllable generation
• 학습 이후 조건을 걸어서 생성과정에 변화
• Conditional reverse-time SDE는 unconditional score로부터 효율적으로 계산됨
• Class-conditional generation, image inpainting, colorization
• Unified picture
• SMLD와 DDPM은 다른 SDE의 discretization으로 통합 가능
• SDE 자체로 이익이지만, 다른 디자인과 결합할 수 있음

6. Background
6
• Denoising Score Matching with Langevin Dynamics (SMLD)
• Notation
• 𝑝𝜎 ෤
𝐱 𝐱 ≜ 𝒩 ෤
𝐱; 𝐱, 𝜎2
I : a perturbation kernel
• 𝑝𝜎 ෤
𝐱 ≜ ∫ 𝑝data 𝐱 𝑝𝜎 ෤
𝐱 𝐱 d𝐱 (𝑝data : the data distribution)
• 𝜎min = 𝜎1 < 𝜎2 < ⋯ < 𝜎𝑁 = 𝜎max : a sequence of positive noise scales
• 𝑝𝜎min
𝐱 ≈ 𝑝data 𝐱 / 𝑝𝜎m𝑎𝑥
𝐱 ≈ 𝒩 x; 𝟎, 𝜎max
2
𝐈
• Noise Conditional Score Network (NCSN) : 𝒔𝜃 𝐱, 𝜎
• A weighted sum of denoising score matching
𝜃∗
= argmin𝜃 ෍
𝑖=1
𝑁
𝜎𝑖
2
𝔼𝑝data 𝐱 𝔼𝑝𝜎𝑖
෤
𝐱 𝐱 𝐬𝜃 ෤
𝐱, 𝜎𝑖 − ∇෤
𝐱 log𝑝𝜎𝑖
෤
𝐱 𝐱
2
2
• 충분한 데이터와 모델 용량이 주어지면 optimal score-based model 𝐬𝜃∗ 𝐱, 𝜎 은 𝜎 ∈ 𝜎𝑖 𝑖=1
𝑁
에서 ∇𝐱 log𝑝𝜎 𝐱 와 같아짐

7. Background
7
• Denoising Score Matching with Langevin Dynamics (SMLD)
• Noise Conditional Score Network (NCSN) : 𝒔𝜃 𝐱, 𝜎
• A weighted sum of denoising score matching
𝜃∗
= argmin𝜃 ෍
𝑖=1
𝑁
𝜎𝑖
2
𝔼𝑝data 𝐱 𝔼𝑝𝜎𝑖
෤
𝐱 𝐱 𝐬𝜃 ෤
𝐱, 𝜎𝑖 − ∇෤
x log 𝑝𝜎𝑖
෤
𝐱 𝐱
2
2
• 충분한 데이터와 모델 용량이 주어지면 optimal score-based model 𝐬𝜃∗ 𝐱, 𝜎 은 𝜎 ∈ 𝜎𝑖 𝑖=1
𝑁
에서 ∇𝐱 log𝑝𝜎 𝐱 와 같아짐
• 각 𝑝𝜎𝑖
x 에서 샘플을 얻기 위해 Langevin MCMC를 𝑀 step 수행
𝐱𝑖
𝑚
= 𝐱𝑖
𝑚−1
+ 𝜖𝑖𝐬𝜃∗ 𝐱𝑖
𝑚−1
, 𝜎𝑖 + 2𝜖𝑖𝐳𝑖
𝑚
• 𝜖𝑖 > 0 : the step size / 𝐳𝑖
𝑚
: standard normal
• 𝑖 = 𝑁, 𝑁 − 1, … , 1을 반복 (𝐱𝑁
0
≈ 𝒩 𝐱 𝟎, 𝜎max
2
𝐈 , 𝐱𝑖
0
= 𝐱𝑖+1
𝑀
when 𝑖 < 𝑁)
• 𝑀 → ∞ and 𝜖𝑖 → 0 for all 𝑖, 𝐱1
𝑁
은 𝑝𝜎min
𝐱 ≈ 𝑝data 𝐱 의 샘플

8. Background
8
• Denoising Diffusion Probabilistic Models (DDPM)
• A sequence of positive noise scales 0 < 𝛽1, 𝛽2, … , 𝛽𝑁 < 1
• A discrete Markov chain 𝐱0, 𝐱1, … , 𝐱𝑁
• 𝑝 𝐱𝑖 𝐱𝑖−1 = 𝒩 𝐱𝑖; 1 − 𝛽𝑖𝐱𝑖−1, 𝛽𝑖𝐈 → 𝑝𝛼𝑖
𝐱𝑖 𝐱0 = 𝒩 𝐱𝑖; 𝛼𝑖𝐱0, 1 − 𝛼𝑖 𝐈 (𝛼𝑖 ≜ Π𝑗=1
𝑖
1 − 𝛽𝑗 )
• The perturbed data distribution : 𝑝𝛼𝑖
෤
x ≜ ∫ 𝑝data 𝐱 𝑝𝛼𝑖
෤
𝐱 𝐱 dx
• A variational Markov chain in the reverse direction : 𝑝𝜃 𝐱𝑖−1 𝐱 = 𝒩 𝐱𝑖−1;
1
1−𝛽𝑖
𝐱𝑖 + 𝛽𝑖𝐬𝜃 𝐱𝑖, 𝑖 , 𝛽𝑖𝐈
• A re-weighted variant of the evidence lower bound (ELBO)
𝜃∗
= argmin𝜃 ෍
𝑖=1
𝑁
1 − 𝛼𝑖 𝔼𝑝data 𝐱 𝔼𝑝𝛼𝑖
෤
𝐱 𝐱 𝐬𝜃 ෤
𝐱, 𝑖 − ∇෤
𝐱 log 𝑝𝛼𝑖
෤
𝐱 𝐱
2
2

9. Background
9
• Denoising Diffusion Probabilistic Models (DDPM)
• The estimated reverse Markov chain (ancestral sampling)
𝐱𝑖−1 =
1
1 − 𝛽𝑖
𝐱𝑖 + 𝛽𝑖𝑠𝜃∗ 𝐱𝑖, 𝑖 + 𝛽𝑖𝐳𝑖, 𝑖 = 𝑁, 𝑁 − 1, … , 1
• 𝜎𝑖
2
∝ 1/𝔼 ∇𝐱 log 𝑝𝜎𝑖
෤
𝐱 𝐱
2
2
• 1 − 𝛼𝑖 ∝ 1/𝔼 ∇𝐱 log𝑝𝜎𝑖
෤
𝐱 𝐱
2
2

10. Score-based Generative Modeling with SDEs
10
• Contribution
→ generalize these ideas further to an infinite number of noise scales

11. Score-based Generative Modeling with SDEs
11
• Perturbing Data with SDEs
• 목표 : a diffusion process 𝐱 𝑡 𝑡=0
𝑇
indexed by a continuous time variable 𝑡 ∈ 0, 𝑇
• x 0 ∼ 𝑝0 for which we have a dataset of i.i.d. samples (𝑝0 : the data distribution)
• x 𝑇 ∼ 𝑝𝑇 for which we have a tractable form to generate samples efficiently (𝑝𝑇 : the prior distribution)
d𝐱 = 𝐟 𝐱, 𝑡 d𝑡 + 𝑔 𝑡 d𝐰
• 𝐱 0 ∼ 𝑝0 : the data distribution / 𝐱 𝑇 ∼ 𝑝𝑇 : the prior distribution
• 𝐰 : the standard Wiener process (a.k.a., Brownian motion)
• 𝐟 ⋅, 𝑡 ∶ ℝ𝑑
→ ℝ𝑑
: a vector-valued function called the drift coefficient of 𝐱 𝑡
• 𝑔 ⋅ ∶ ℝ → ℝ : a scalar function known as the diffusion coefficient of 𝐱 𝑡
• 쉬운 계산을 위해 scalar로 가정 (𝑑 × 𝑑 matrix)
• State와 time이 전체적으로 Lipschitz일 때, SDE는 unique strong solution을 가짐
• 𝑝𝑡 𝐱 : the probability density of 𝐱 𝑡
• 𝑝𝑠𝑡 𝐱 𝑡 𝐱 𝑠 : the transition kernel from 𝐱 𝑠 to 𝐱 𝑡 (where 0 ≤ 𝑠 < 𝑡 ≤ 𝑇)

12. Score-based Generative Modeling with SDEs
12
• Generating Samples by Reversing the SDE
• 𝐱 𝑇 ∼ 𝑝𝑇의 샘플을 시작으로 reverse → 𝐱 0 ∼ 𝑝0 생성
d𝐱 = 𝐟 𝐱, 𝑡 − 𝑔 𝑡 2
∇𝐱log 𝑝𝑡 𝐱 d𝑡 + 𝑔 𝑡 d ഥ
𝐰
• ഥ
𝐰 : a standard Wiener process when time flows backwards from 𝑇 from 0
• d𝑡 : an infinitesimal negative timestep
• 모든 𝑡에 대해 marginal distribution ∇𝐱 log 𝑝𝑡 𝐱 가 주어지면
→ reverse diffusion process

13. Score-based Generative Modeling with SDEs
13
• Estimating Scores for the SDE
• The score of a distribution can be estimated by training a score-based model on samples with score
matching.
• Train a time-dependent score-based model 𝐬𝜽 𝐱, 𝑡 via a continuous generalization
𝜽∗
= argmin𝜃𝔼𝑡 𝜆 𝑡 𝔼𝐱 0 𝔼𝐱 𝑡 𝐬𝜽 𝐱 𝑡 , 𝑡 − ∇𝐱 𝑡 log𝑝0𝑡 𝐱 𝑡 𝐱 0 2
2
• 𝜆 ∶ 0, 𝑇 → ℝ+
: a positive weighting function
• With sufficient data and model capacity, 𝐬𝜽∗ 𝐱, 𝑡 = ∇𝐱 log 𝑝𝑡 𝐱 for almost all 𝐱 and 𝑡
• 𝜆 ∝ 1/𝔼 ∇𝐱 𝑡 log 𝑝0𝑡 𝐱 𝑡 𝐱 0 2
2

14. Score-based Generative Modeling with SDEs
14
• Special Cases: VE and VP SDEs
• The noise perturbations used in SMLD and DDPM can be regarded as discretizations of two different SDEs
• Variance Exploding (VE) and Variance Preserving (VP) SDEs
• Each perturbation kernel 𝑝𝜎𝑖
𝐱 𝐱0 of SMLD
𝐱𝑖 = 𝐱𝑖−1 + 𝜎𝑖
2
− 𝜎𝑖−1
2
𝐳𝑖−1, 𝑖 = 1, … , 𝑁
• 𝐳𝑖−1 ∼ 𝒩 𝟎, 𝐈 , 𝜎0 = 0
• 𝑁 → ∞, 𝜎𝑖 𝑖=1
𝑁
= 𝜎 𝑡 , 𝐳𝑖 = 𝐳 𝑡
• The Markov chain 𝐱𝑖 𝑖=1
𝑁
becomes a continuous stochastic process 𝐱 𝑡 𝑡=0
1
with a continuous time variable 𝑡 ∈ 0,1
• The process 𝐱 𝑡 𝑡=0
1
is given by the following SDE
d𝐱 =
d 𝜎2 𝑡
d𝑡
d𝐰

15. Score-based Generative Modeling with SDEs
15
• Special Cases: VE and VP SDEs
• The noise perturbations used in SMLD and DDPM can be regarded as discretizations of two different SDEs
• Variance Exploding (VE) and Variance Preserving (VP) SDEs
• For the perturbation kernels 𝑝𝛼𝑖
𝐱 𝐱0 𝑖=1
𝑁
of DDPM, the discrete Markov chain is
𝐱𝑖 = 1 − 𝛽𝑖𝐱𝑖−1 + 𝛽𝑖𝐳𝑖−1, 𝑖 = 1, ⋯ , 𝑁.
• As 𝑁 → ∞,
d𝐱 = −
1
2
𝛽 𝑡 𝐱d𝑡 + 𝛽 𝑡 d𝐰
• SDE of SMLD : a process with exploding variance when 𝑡 → ∞ : Variance Exploding (VE) SDE
• SDE of DDPM : a process with bounded variance : Variance Preserving (VP) SDE
→ VE and VP SDEs have affine drift coefficients : perturbation kernels 𝑝0𝑡 𝐱 𝑡 𝐱 0 are Gaussian & in closed-form

16. Solving the Reverse SDE
16
• General-Purpose Numerical SDE Solvers
• Numerical solvers provide approximate trajectories from SDEs.
• Euler-Maruyama, stochastic Runge-Kutta methods
• Predictor : SMLD or DDPM → the reverse diffusion sampler

17. Solving the Reverse SDE
17
• Predictor-Corrector Samplers
• Score-based MCMC approaches (e.g., Langevin MCMC, HMC)
• Sample from 𝑝𝑡 directly, and correct the solution of a numerical SDE solver
• The numerical SDE (predictor) → score-based MCMC (corrector)

18. Solving the Reverse SDE
18
• Probability Flow and Equivalence to Neural ODEs
• A corresponding deterministic process
• Trajectories share the same marginal probability densities 𝑝𝑡 𝐱 𝑡=0
𝑇
d𝐱 = 𝐟 𝐱, 𝑡 −
1
2
𝑔 𝑡 2
∇𝐱 log 𝑝𝑡 𝐱 d𝑡
• The probability flow ODE
• Efficient sampling
• Sample 𝐱 0 ∼ 𝑝0 from different final conditions 𝐱 𝑇 ∼ 𝑝𝑇
• Generate competitive samples with a fixed discretization strategy
• The number of function evaluations can be reduced by over 90%
without affecting the visual quality of samples with a large error tolerance.

19. Solving the Reverse SDE
19
• Probability Flow and Equivalence to Neural ODEs
• Manipulating latent representations
• Encode any datapoint 𝐱 0 into a latent space 𝐱 𝑇
• Decoding can be achieved by integrating a corresponding ODE for the reverse-time SDE.
• Interpolation, temperature scaling

20. Controllable Generation
20
• The continuous structure
• Produce data samples from 𝑝0 & 𝑝0 𝐱 𝑡 𝐲 (if 𝑝𝑡 𝐲 𝐱 𝑡 is known)
• Sample from 𝑝𝑡 𝐱 𝑡 𝐲 by starting from 𝑝𝑇 𝐱 𝑇 𝐲 and solving a conditional reverse-time SDE
d𝐱 = 𝐟 𝐱 𝑡 − 𝑔 𝑡 2
∇𝐱 log 𝑝𝑡 𝐱 + ∇𝐱 log 𝑝𝑡 𝐲 𝐱 d𝑡 + 𝑔 𝑡 d ഥ
𝐰
• 𝐲 : class labels → train a time-dependent classifier 𝑝𝑡 𝐲 𝐱 𝑡 for class-conditional sampling

21. Discussion
21
• A framework for score-based generative modeling based on SDEs
• A better understanding of
• Existing approaches
• New sampling algorithms
• Exact likelihood computation
• Uniquely identifiable encoding
• Latent code manipulation
• Conditional generation
• Slower at sampling than GANs on the same datasets
• Combining the stable learning of score-based generative models with the fast sampling of implicit models like GANs
• A number of hyper-parameters
• Automatically select and tune these hyper-parameters

22. 감 사 합 니 다
22