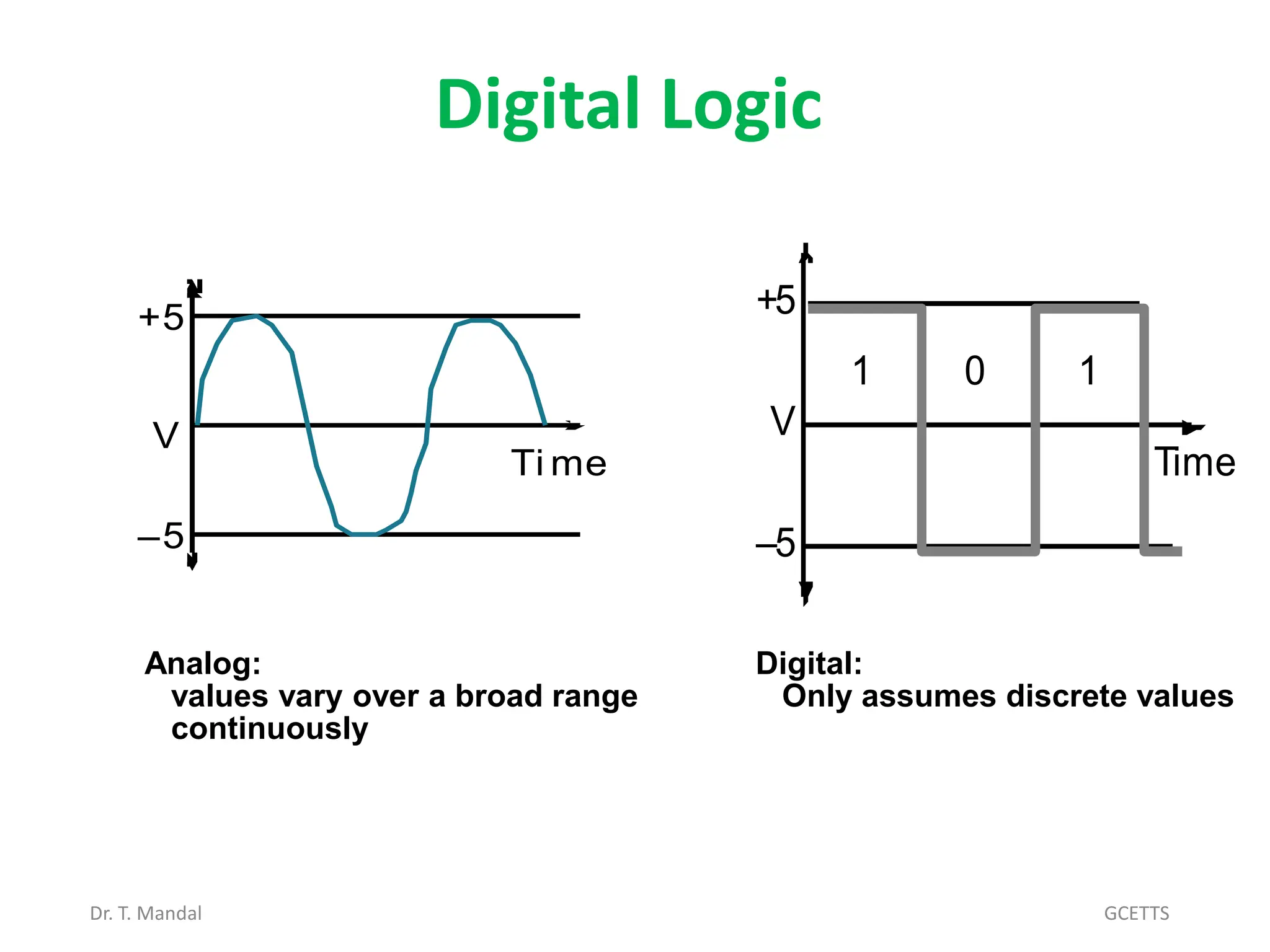
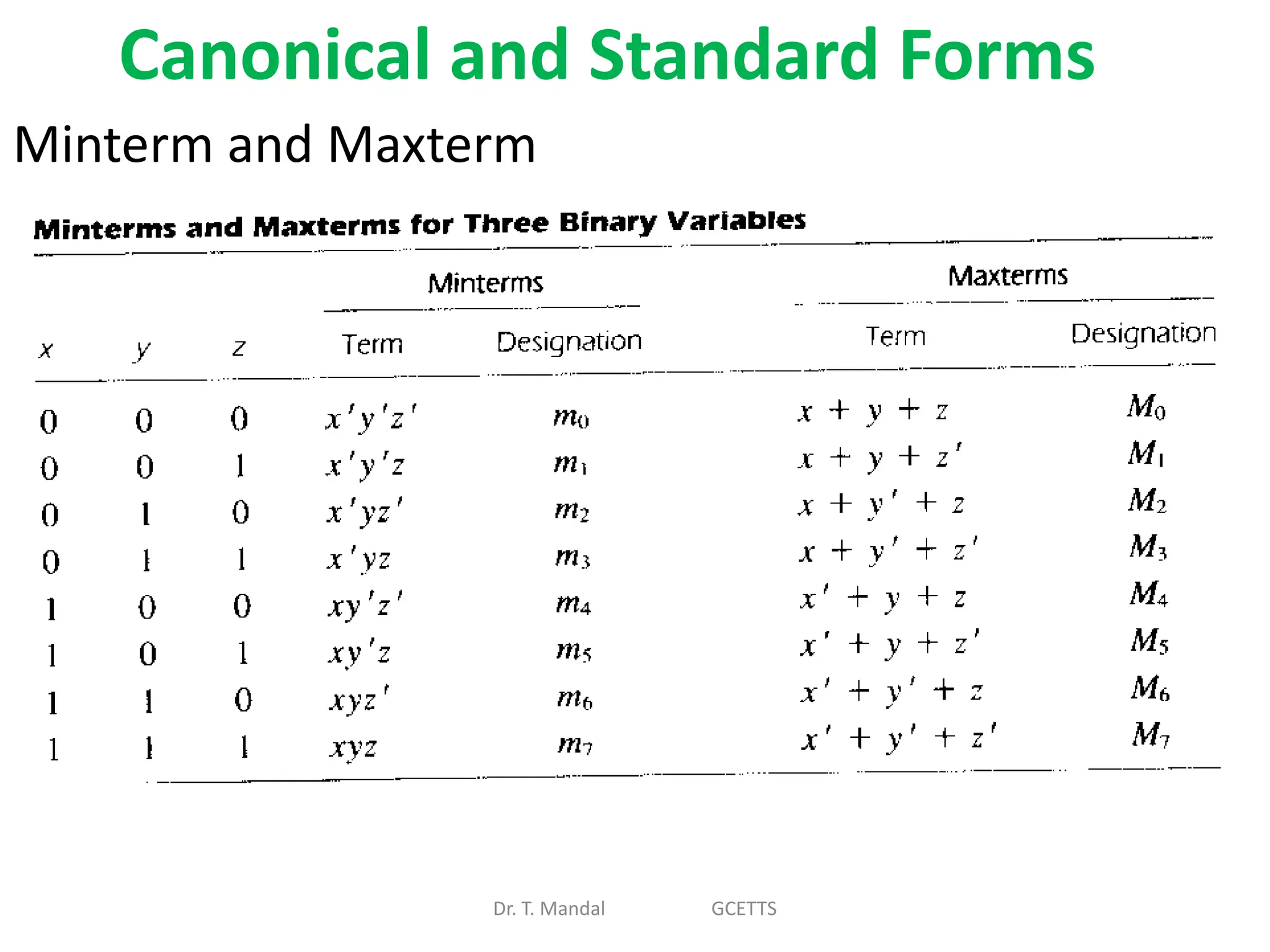
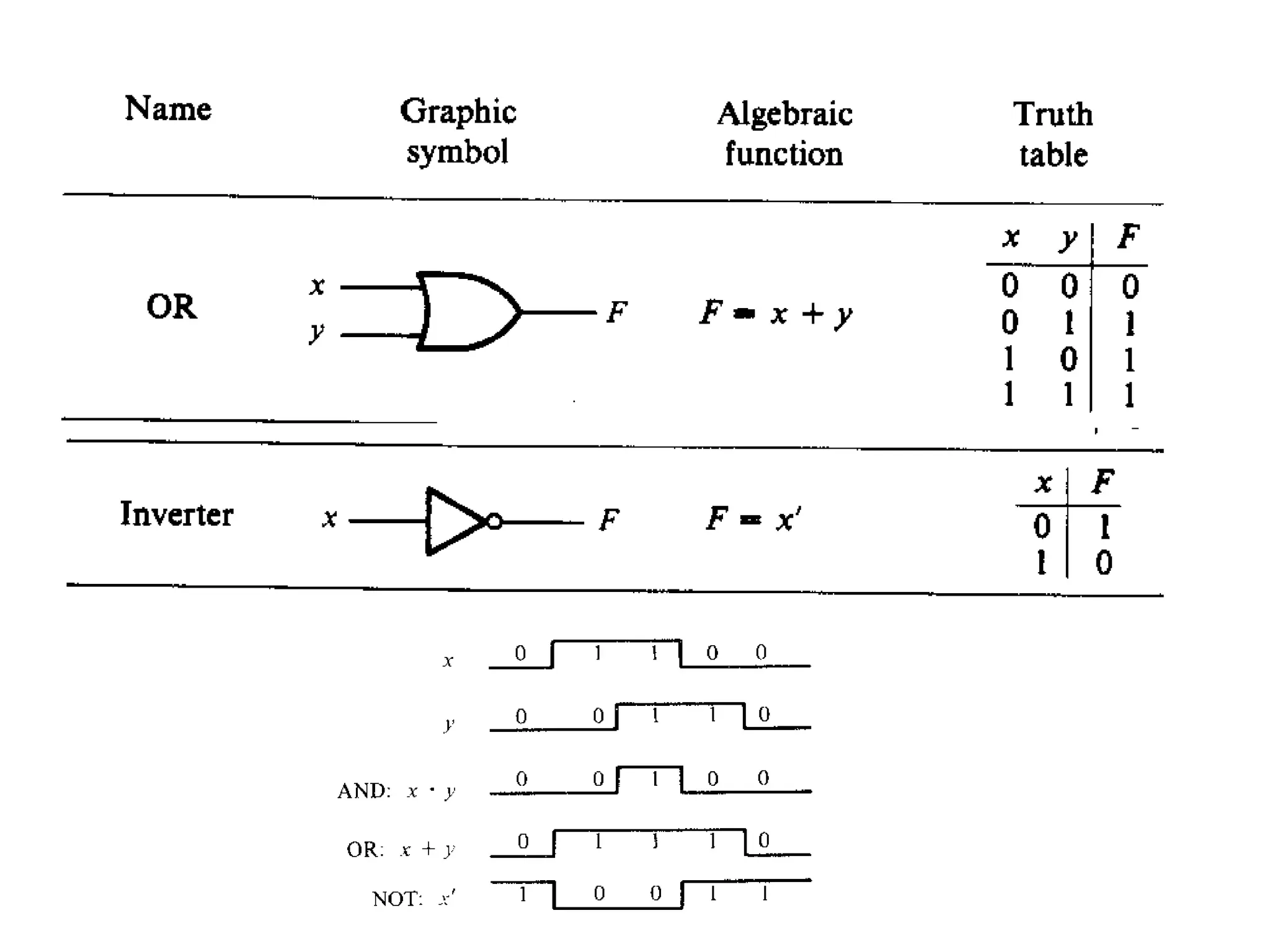
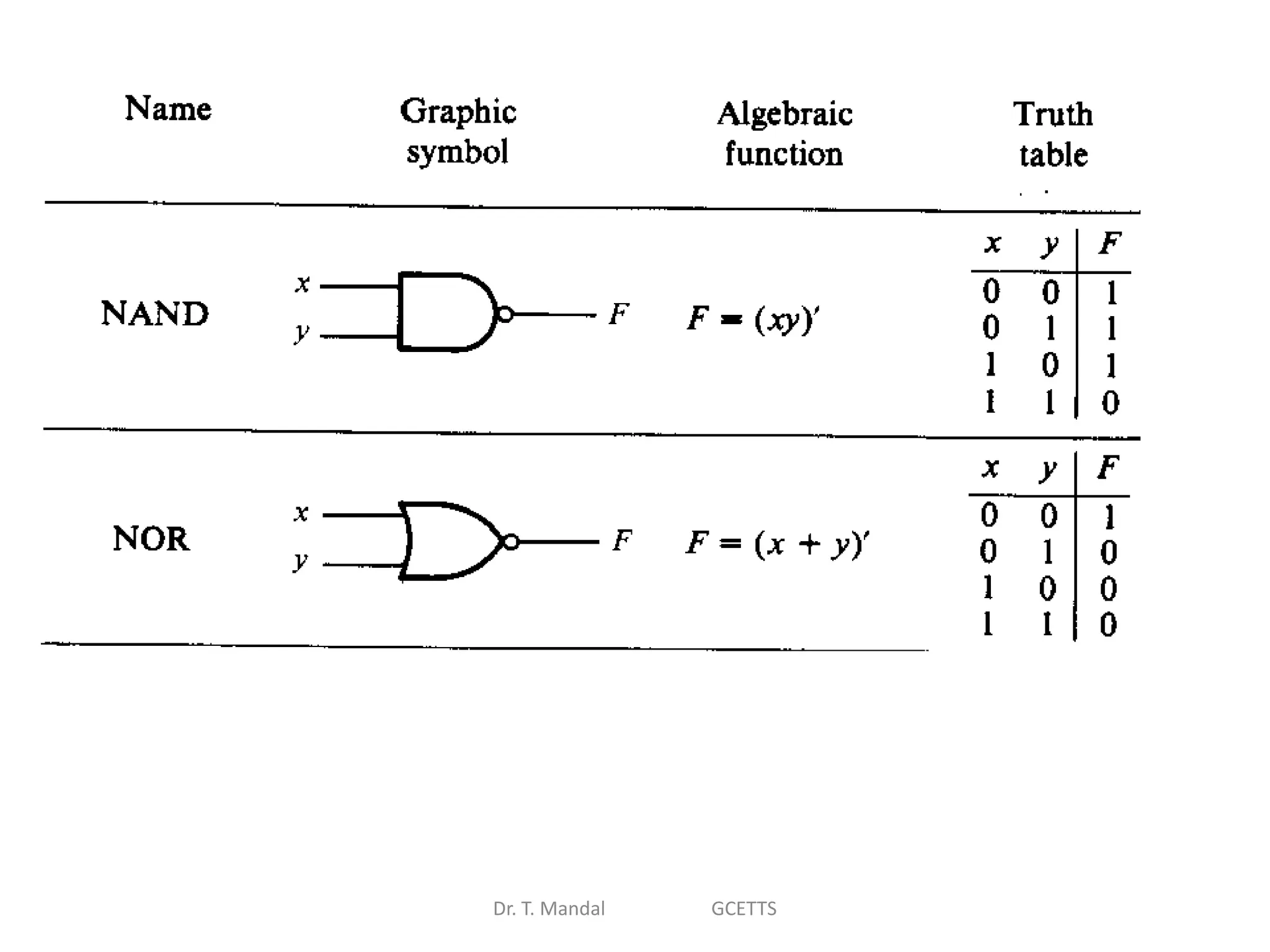
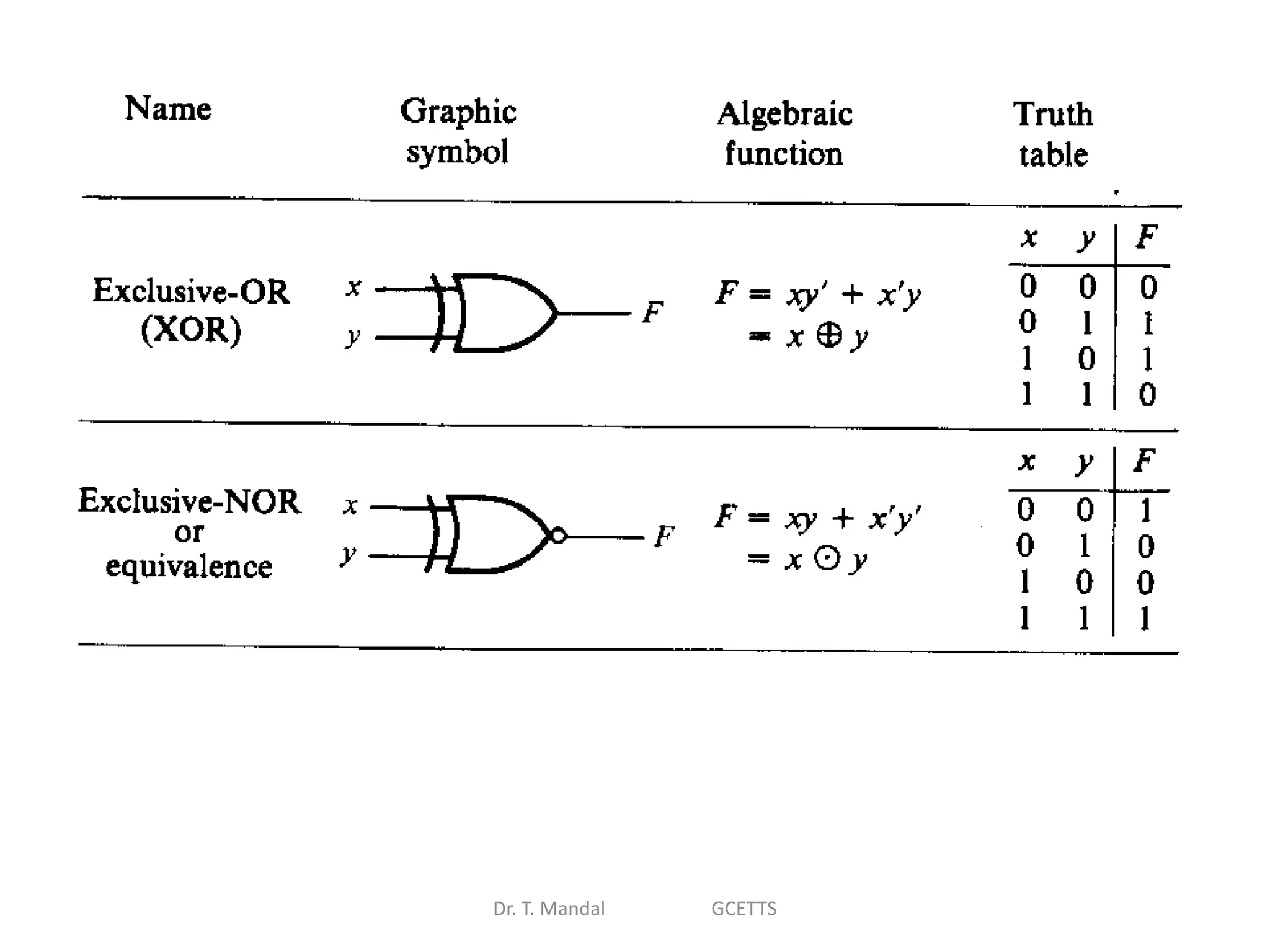
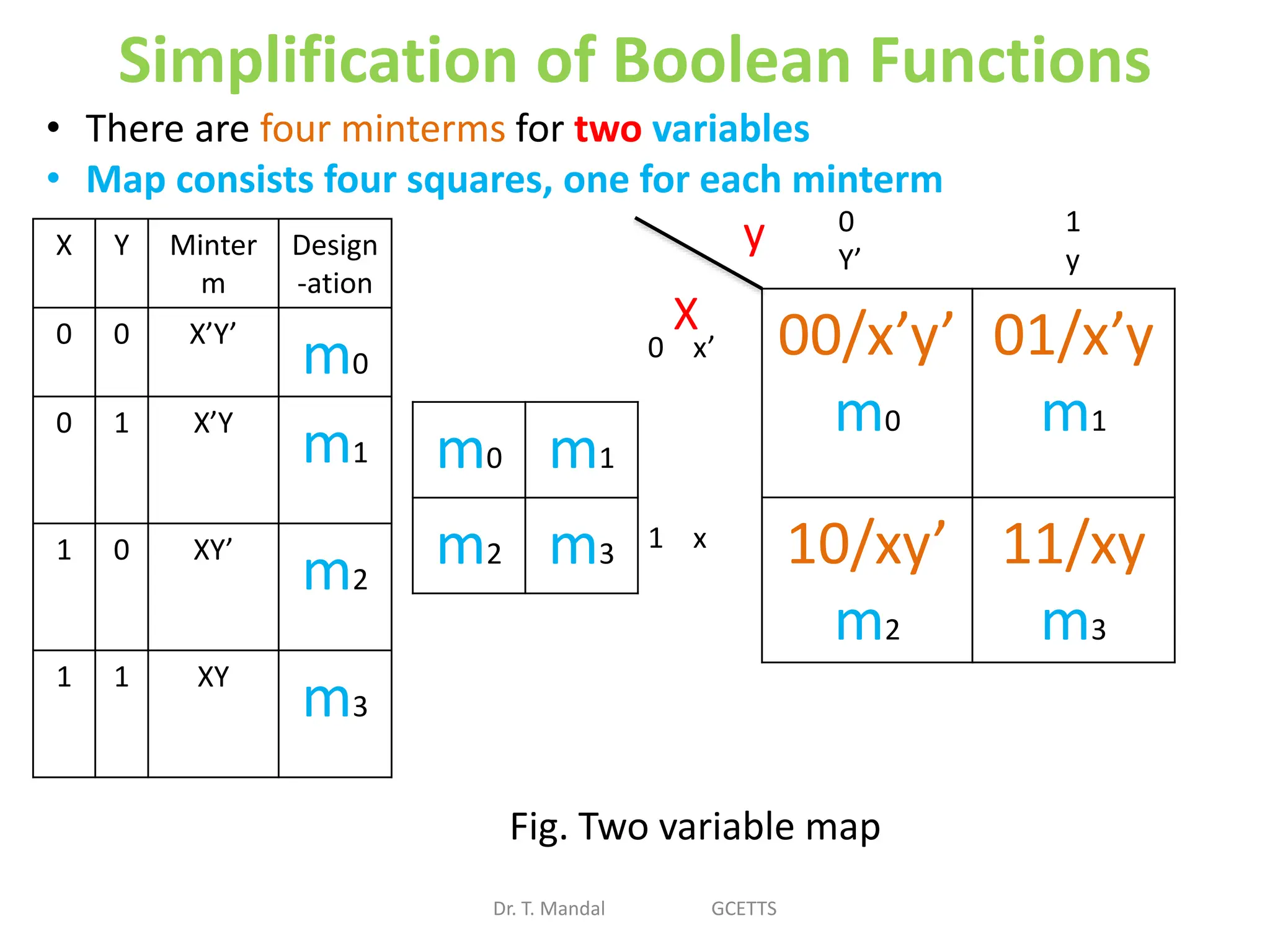
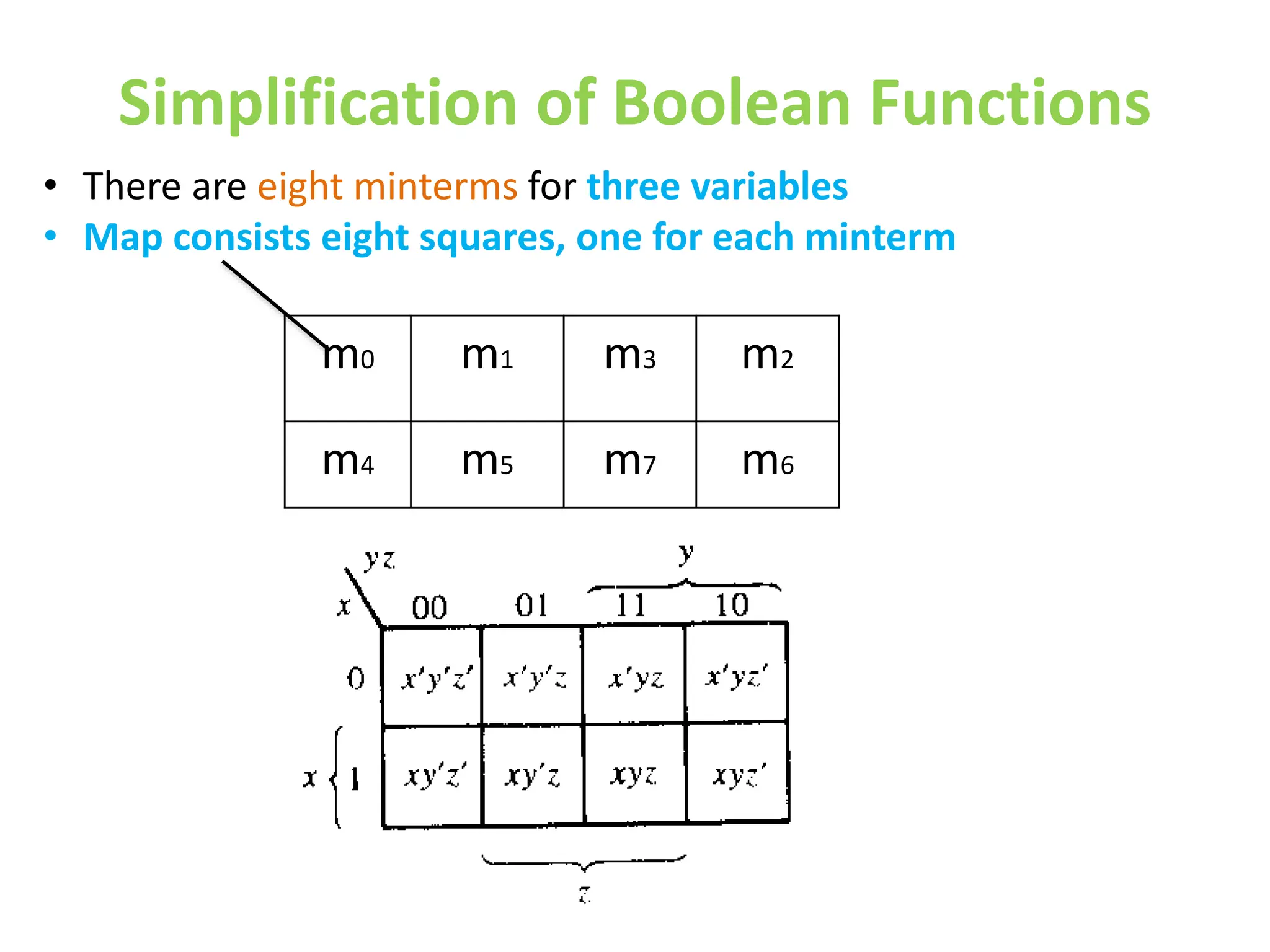
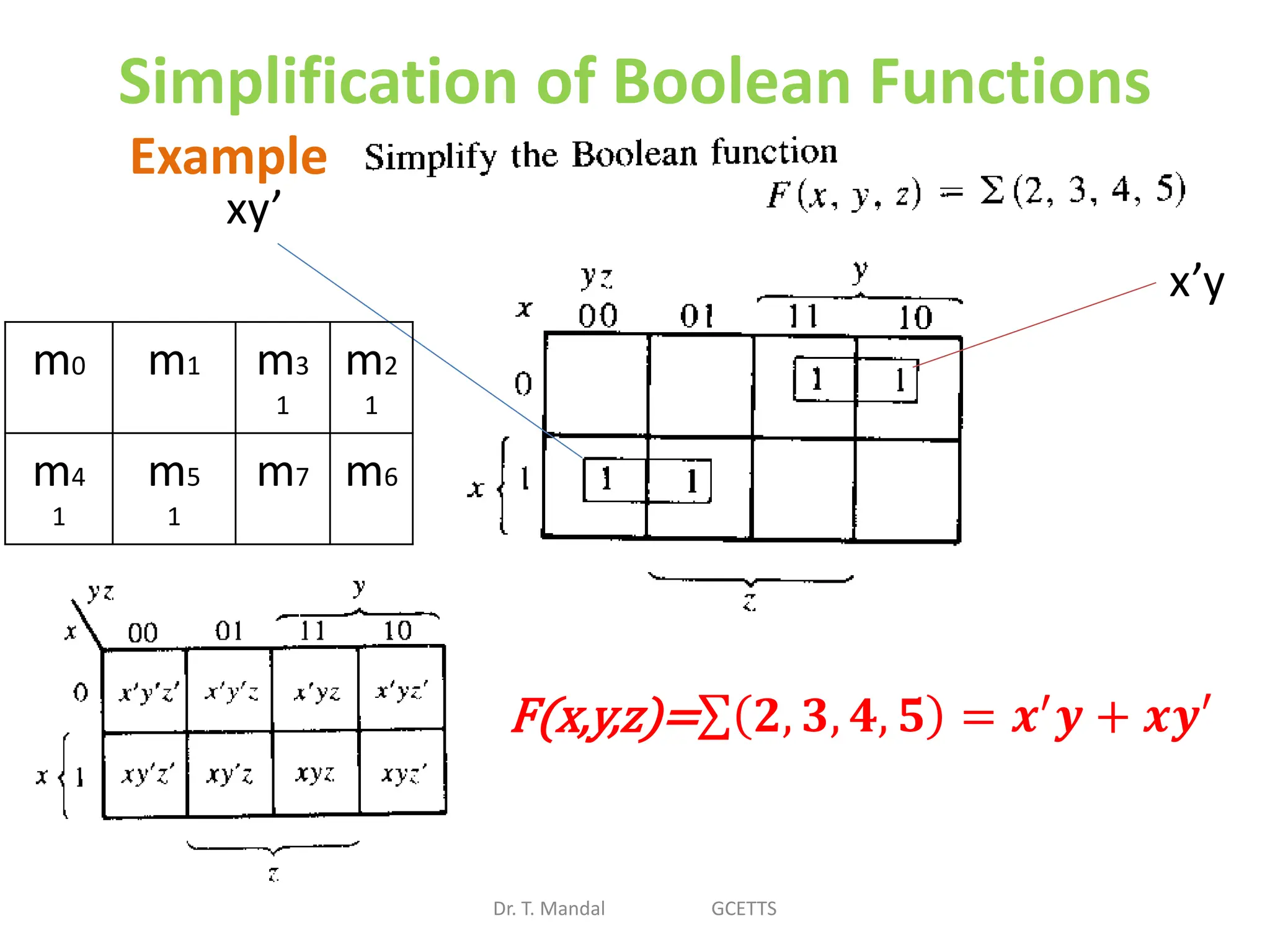
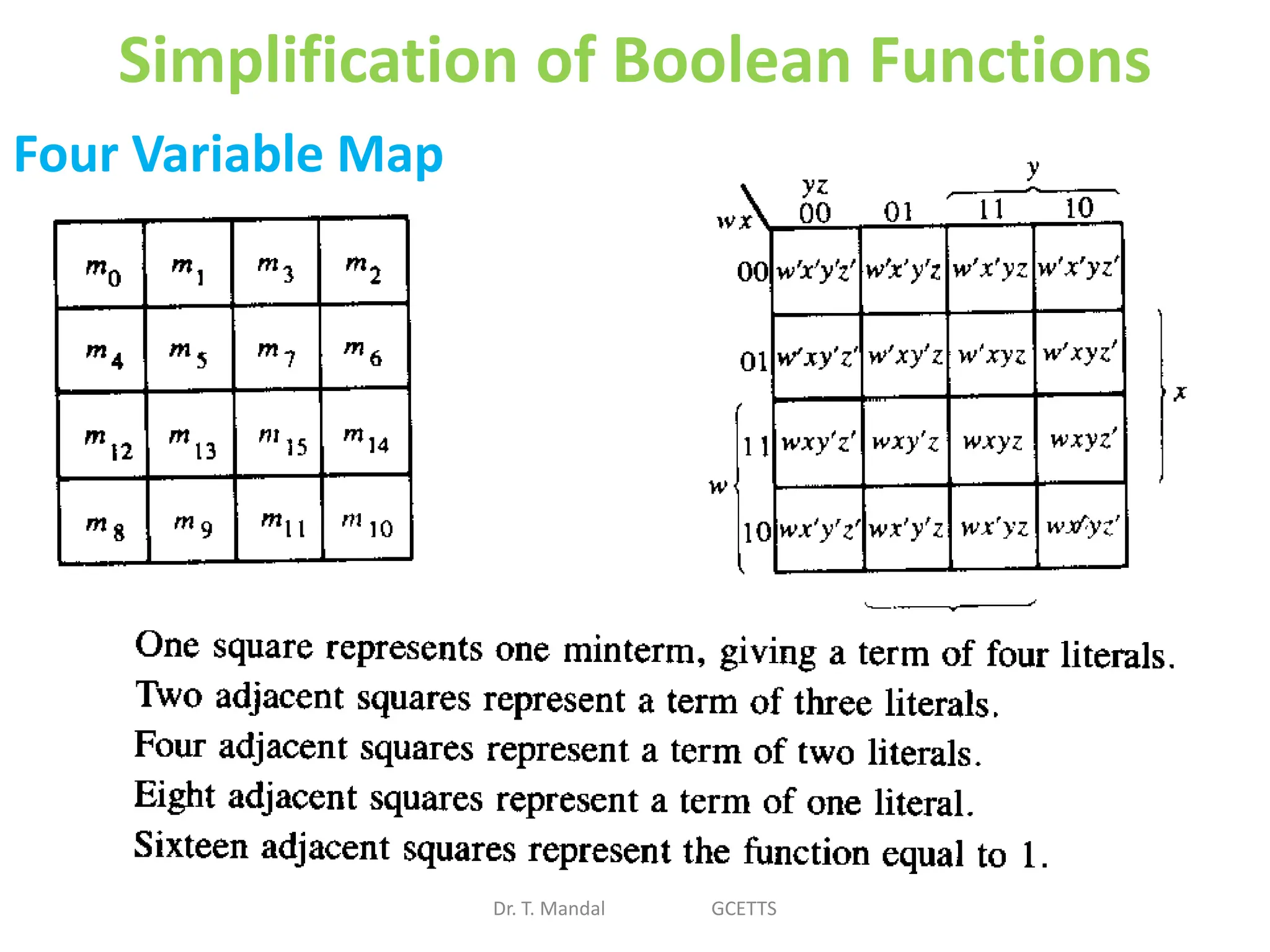
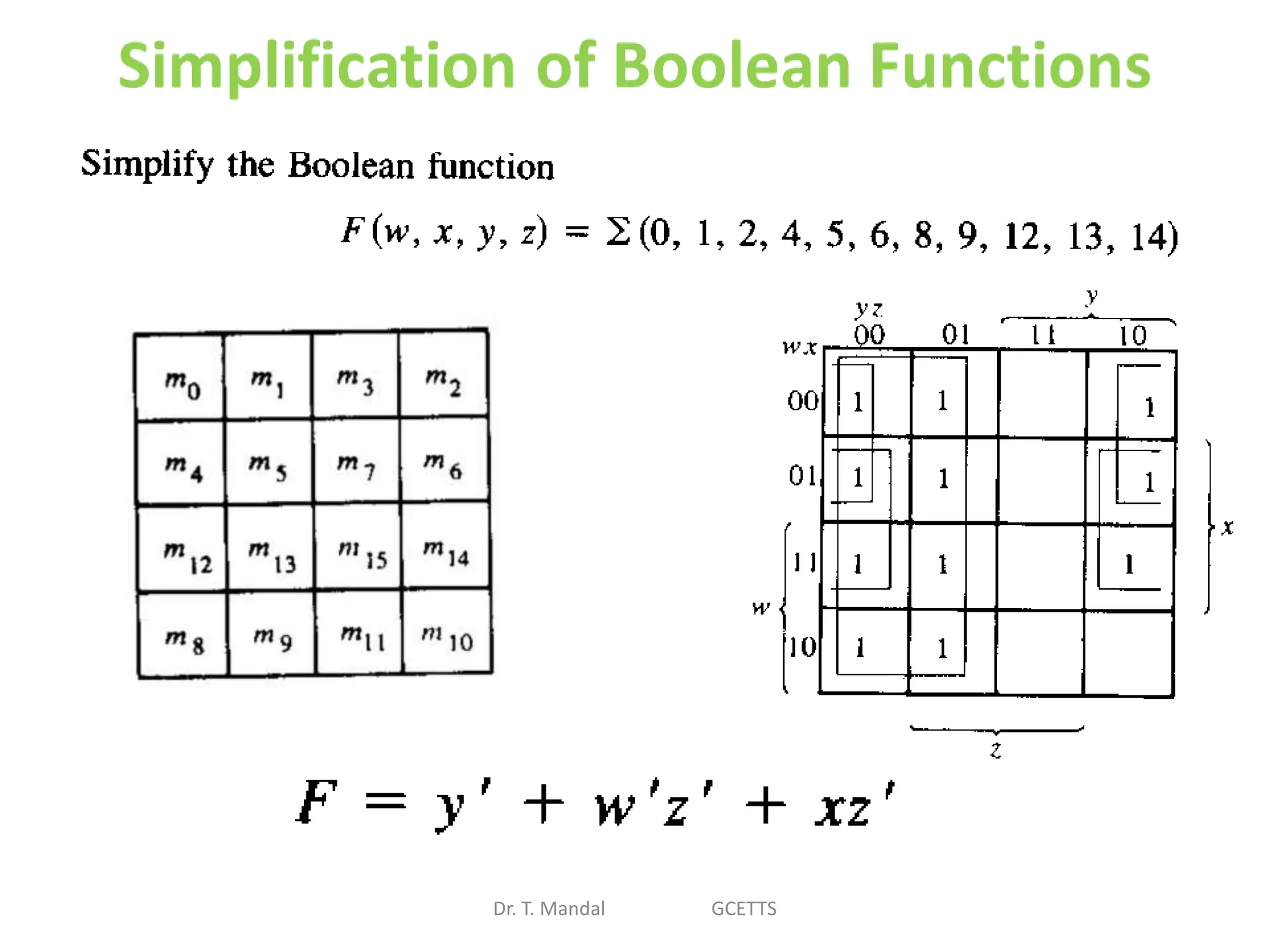
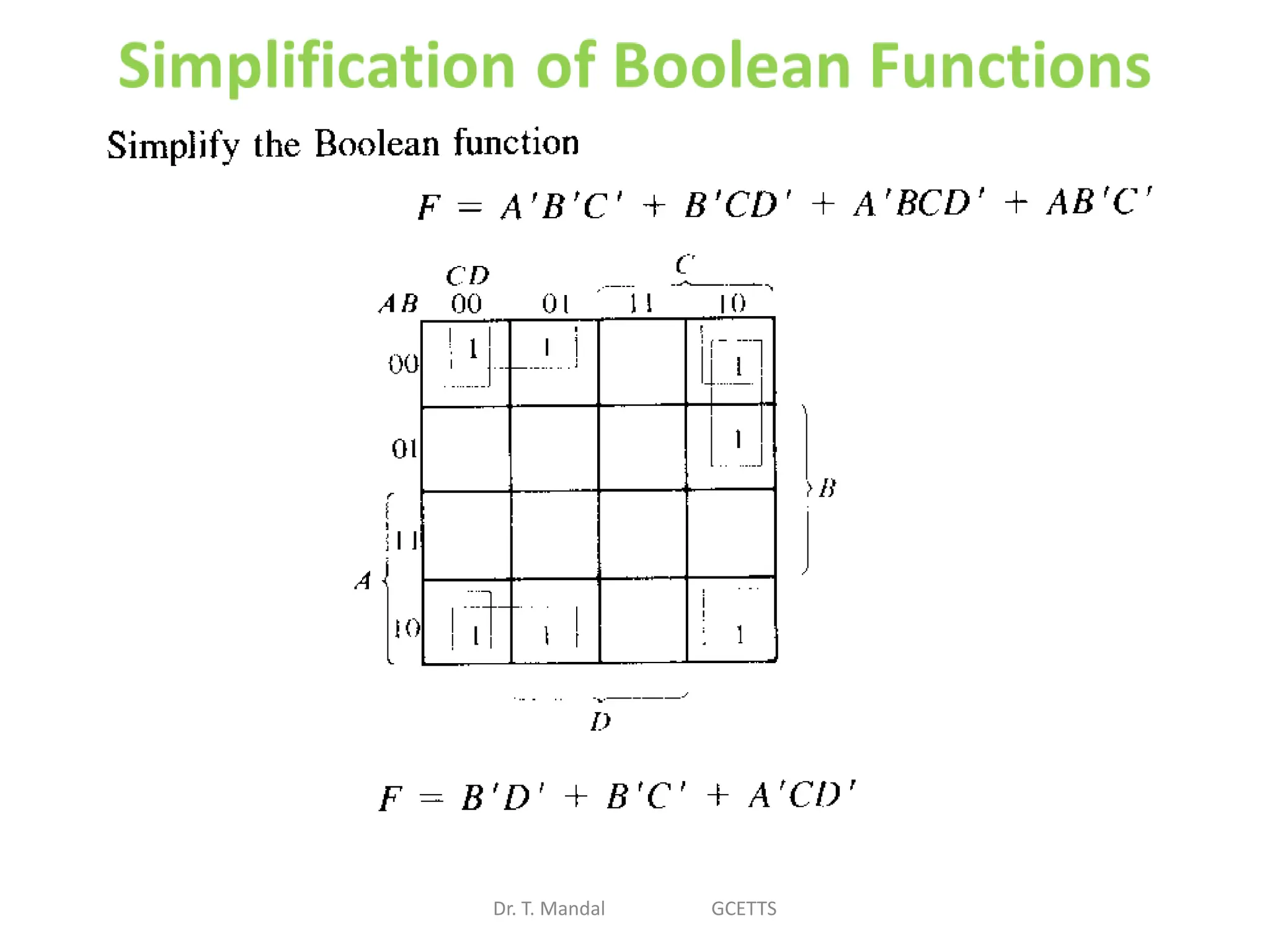
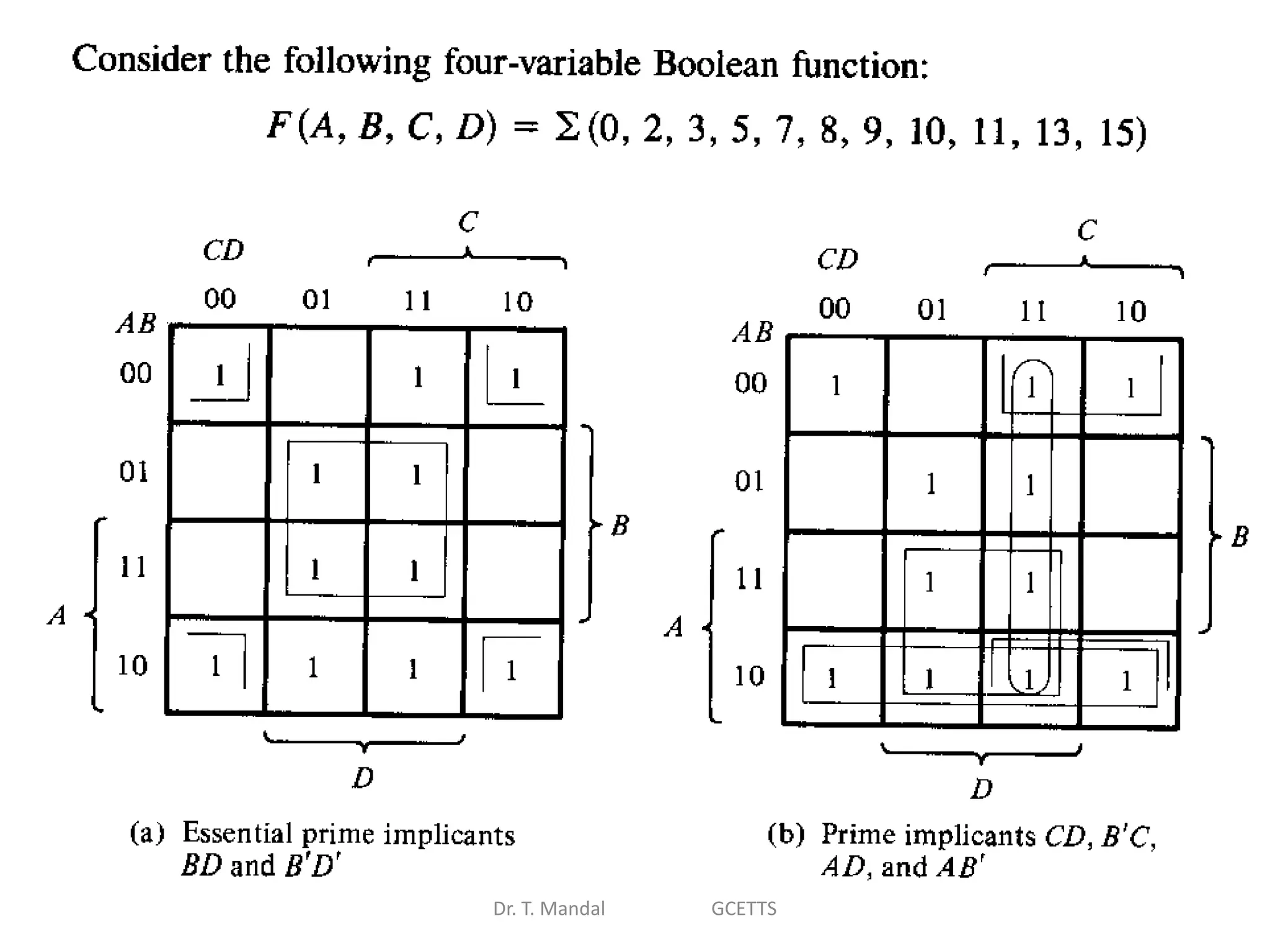
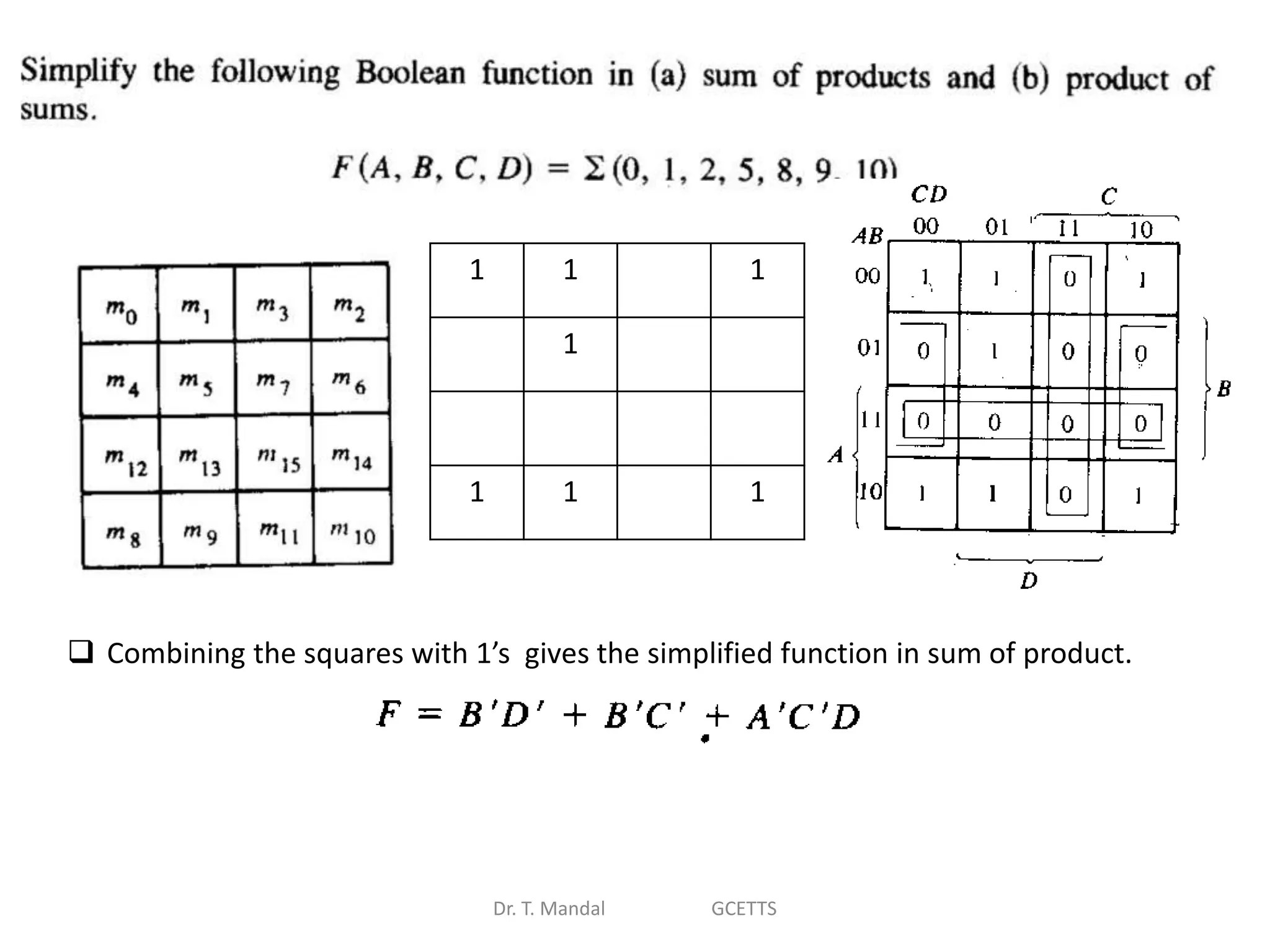
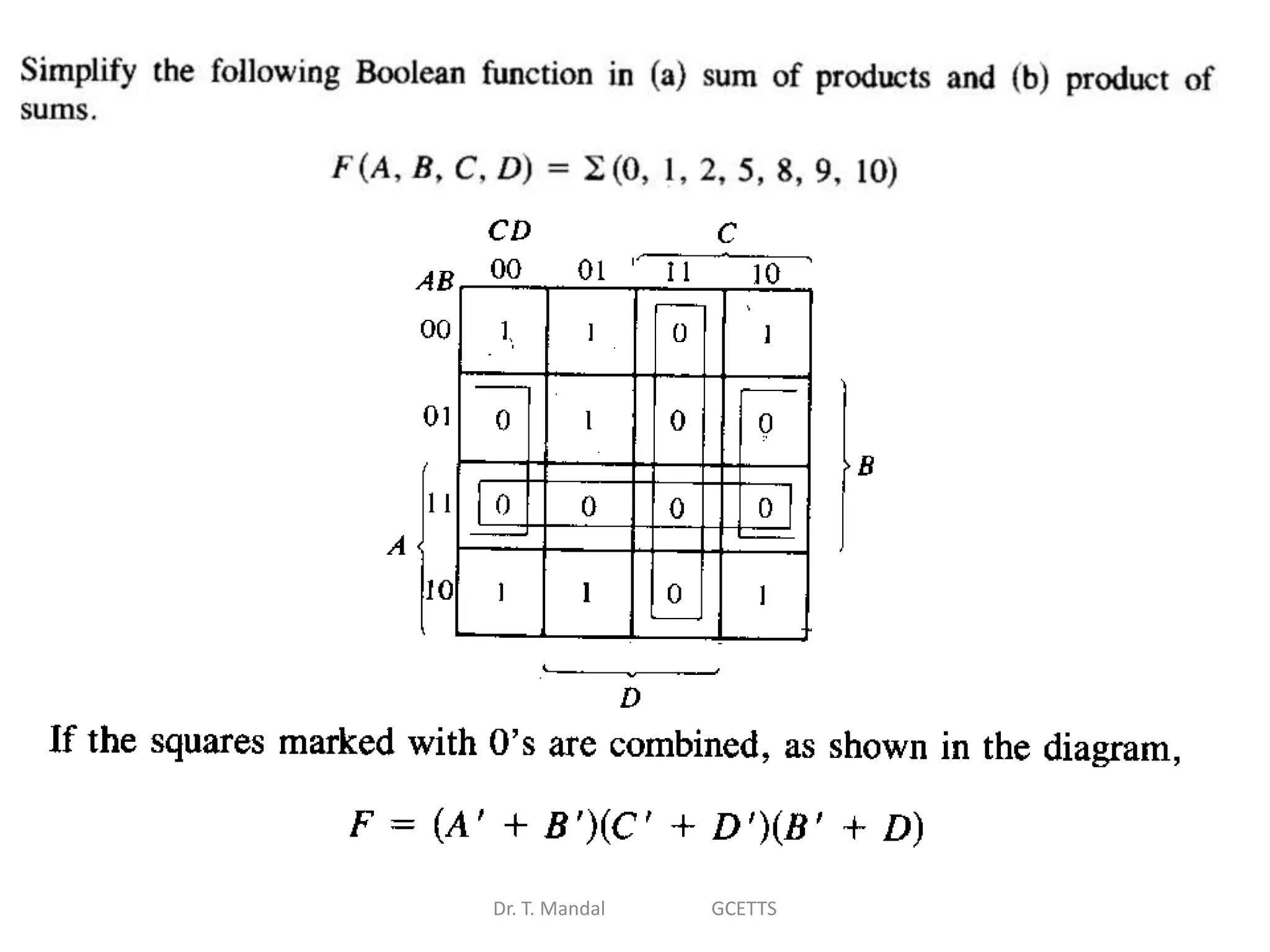
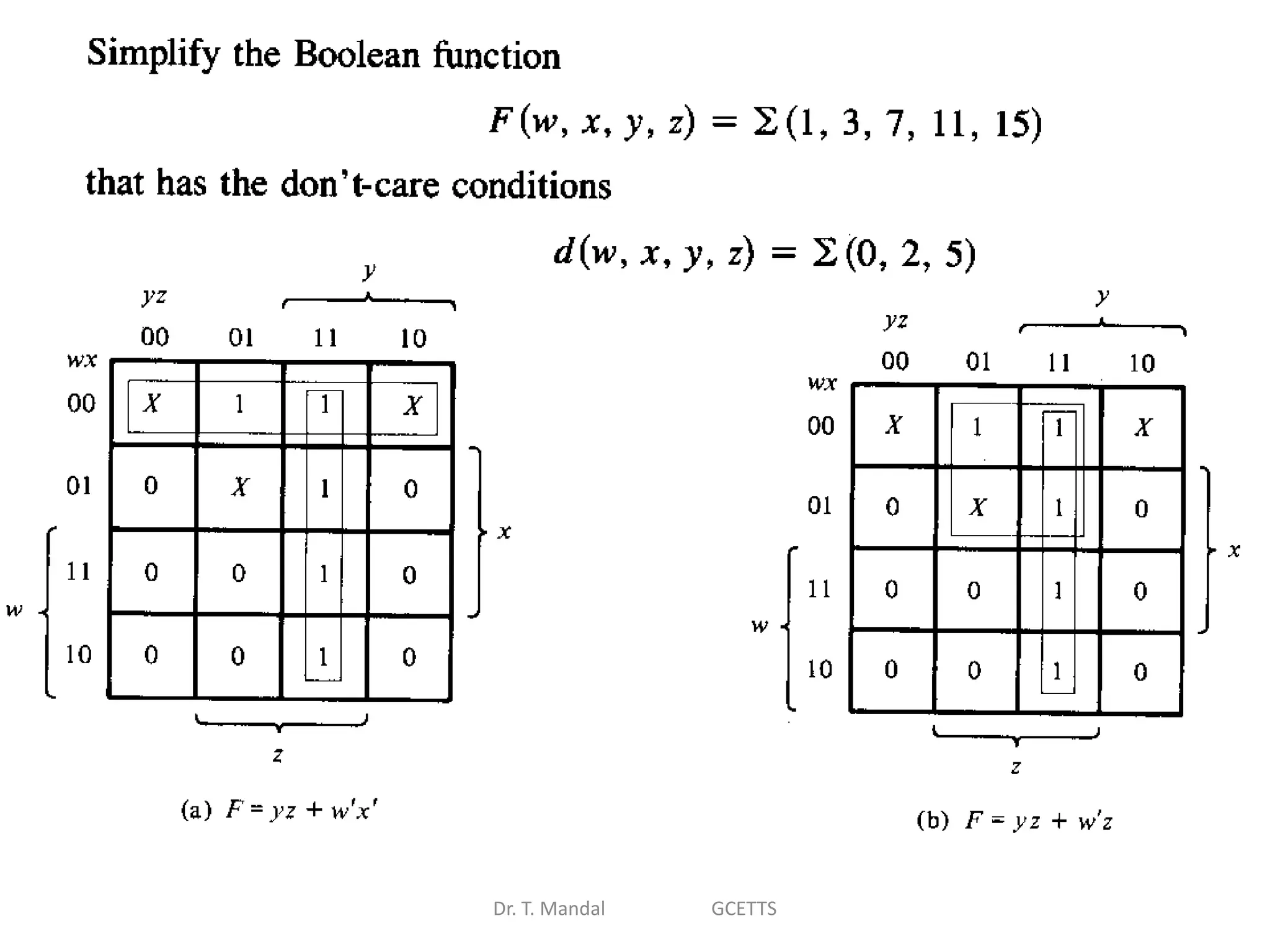
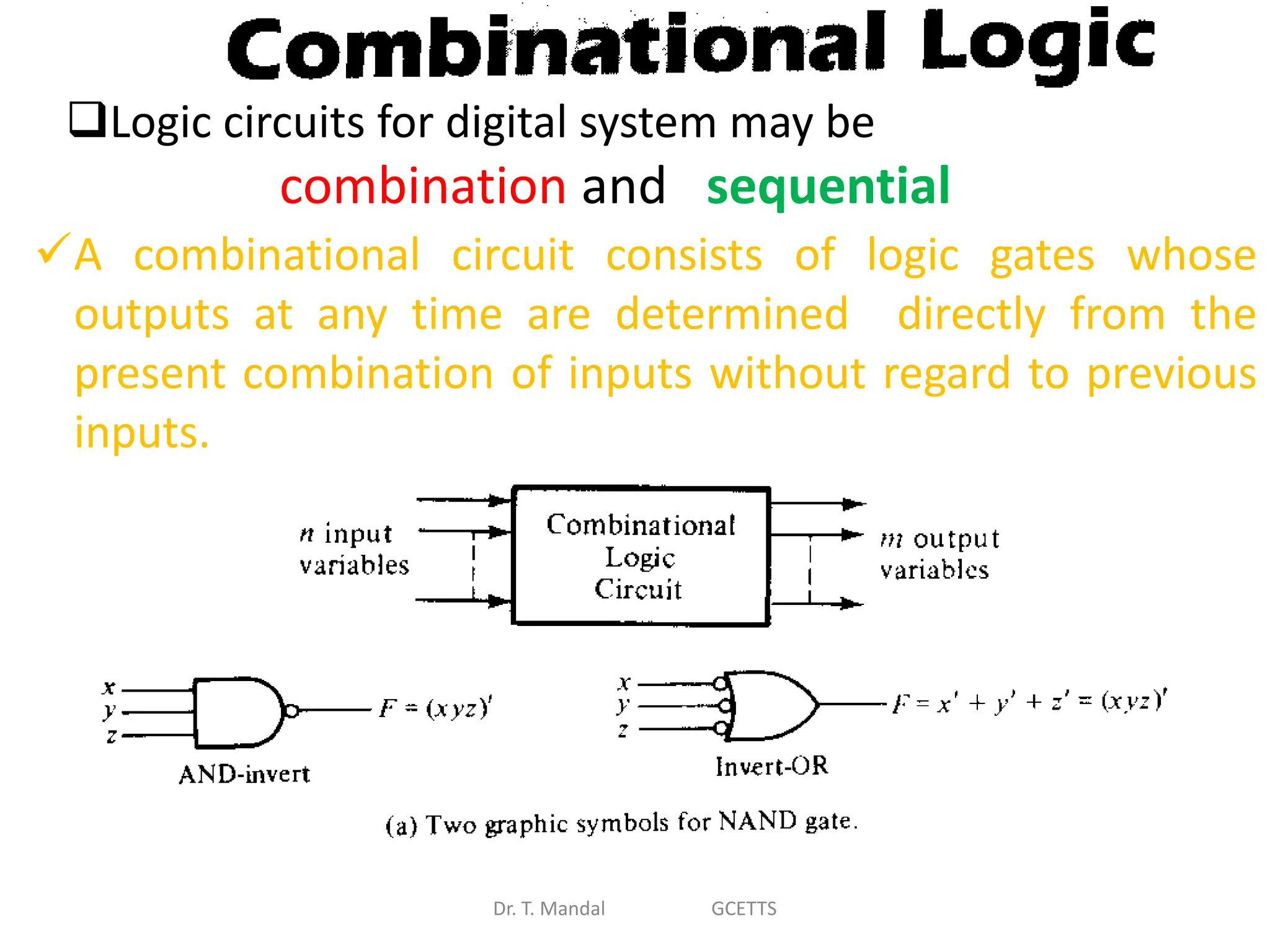
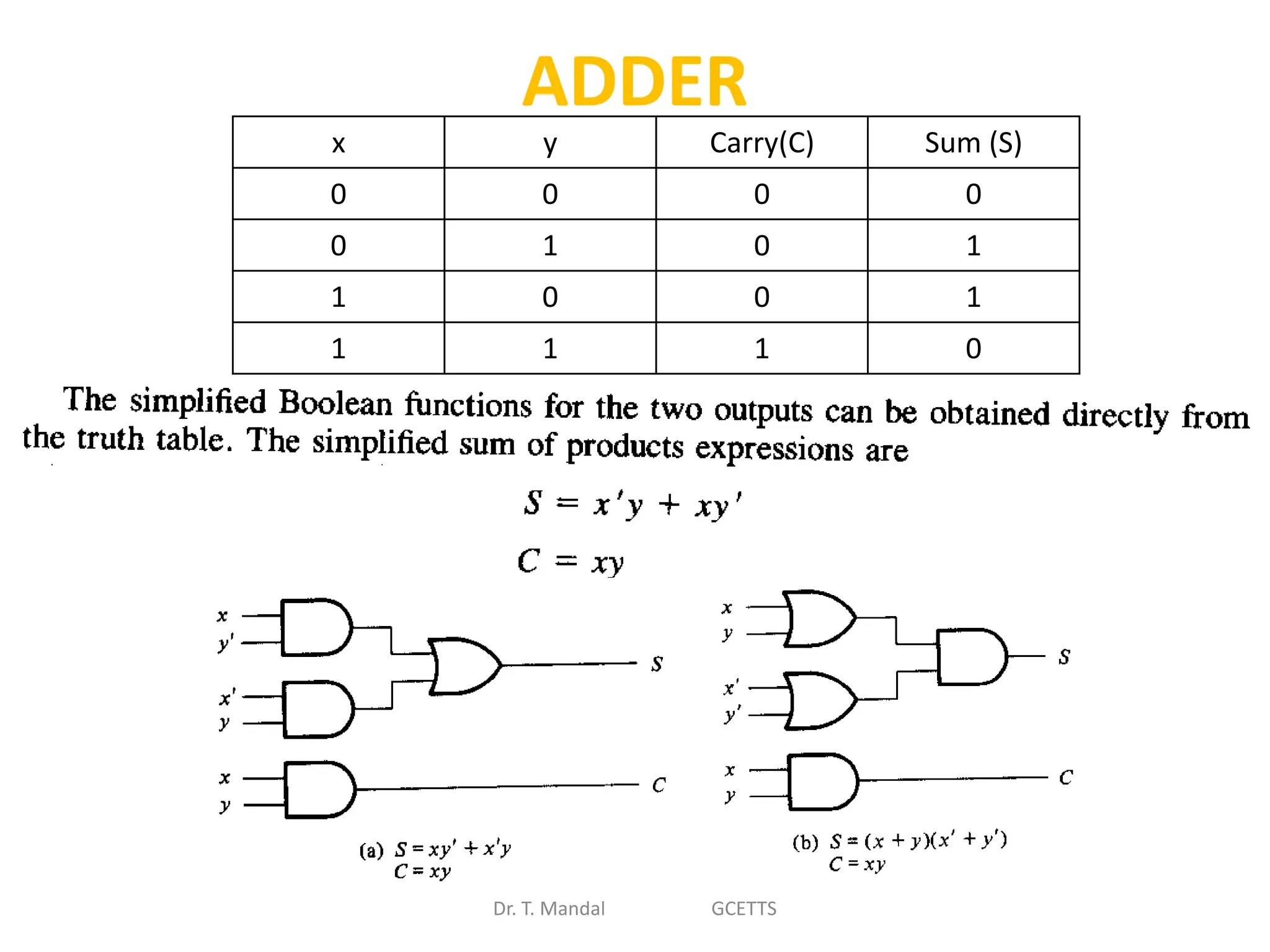
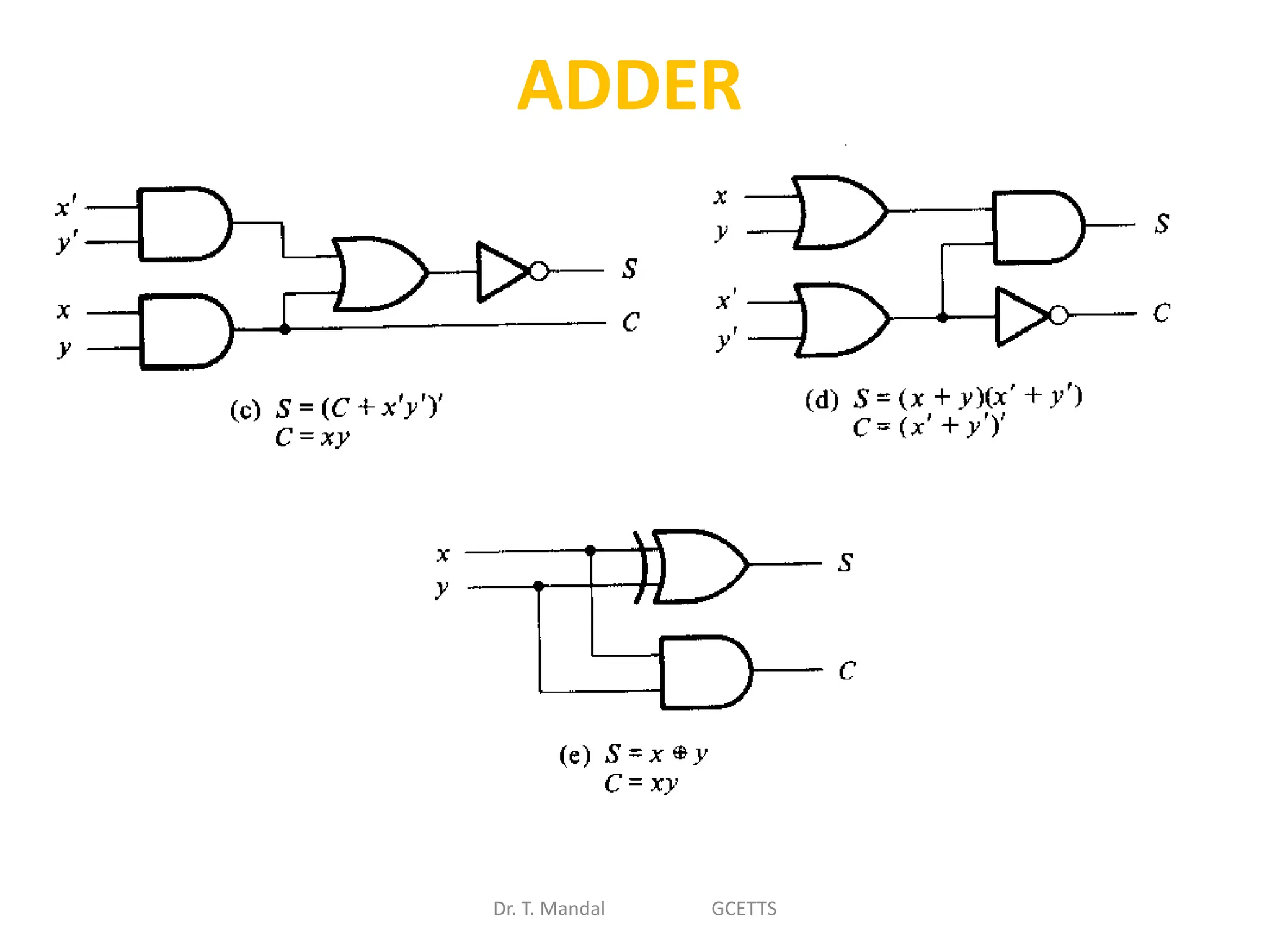
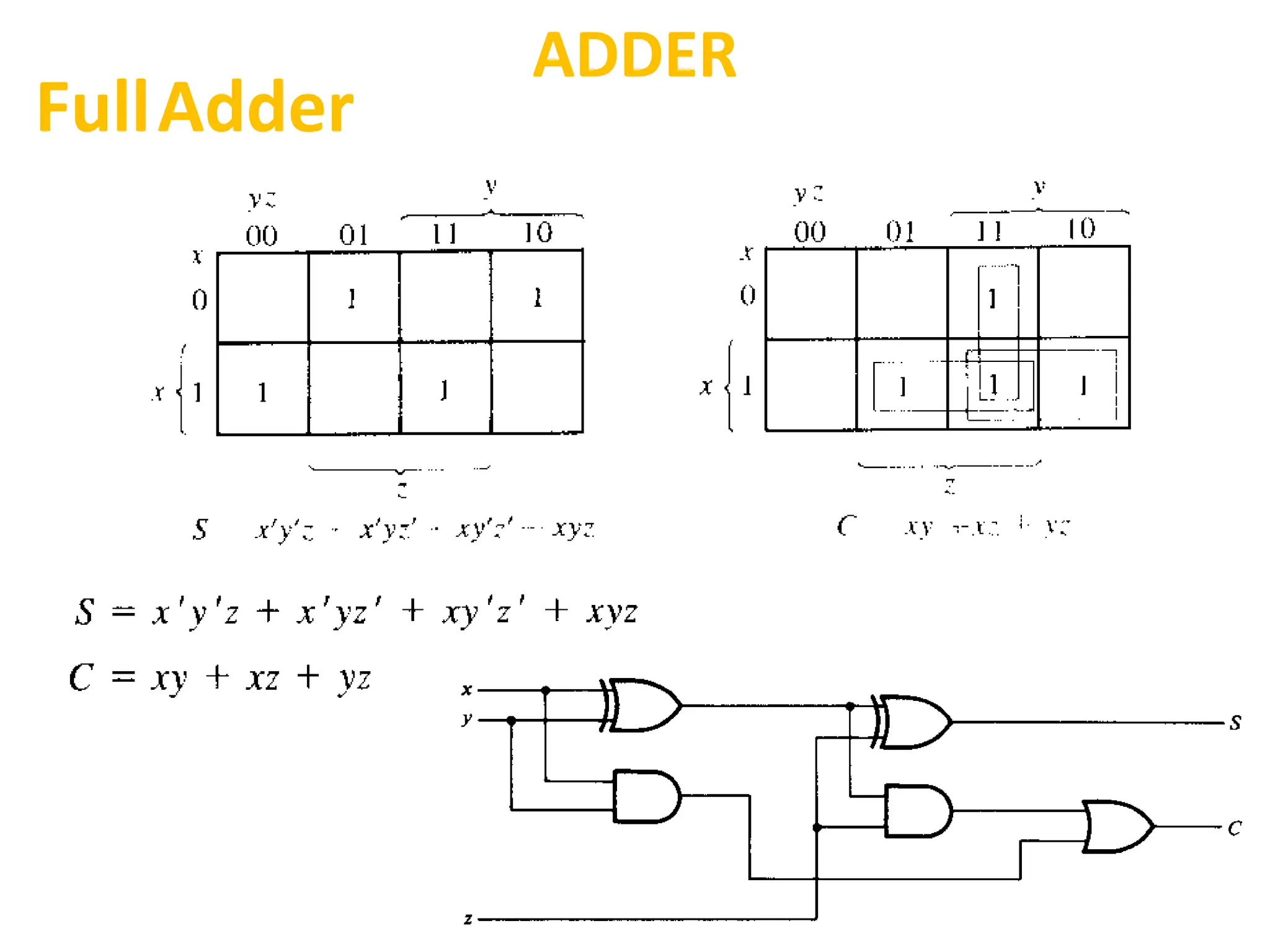
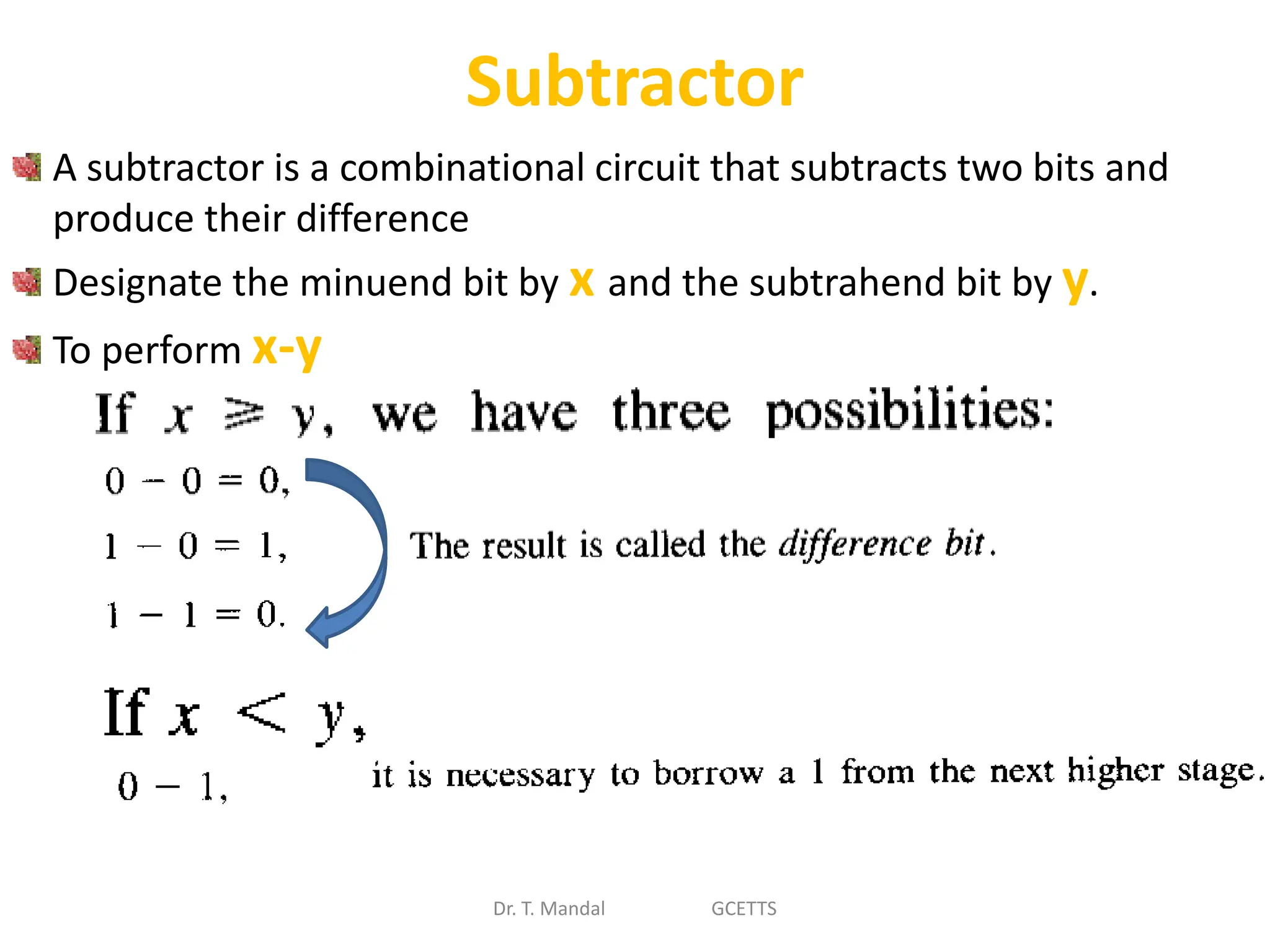
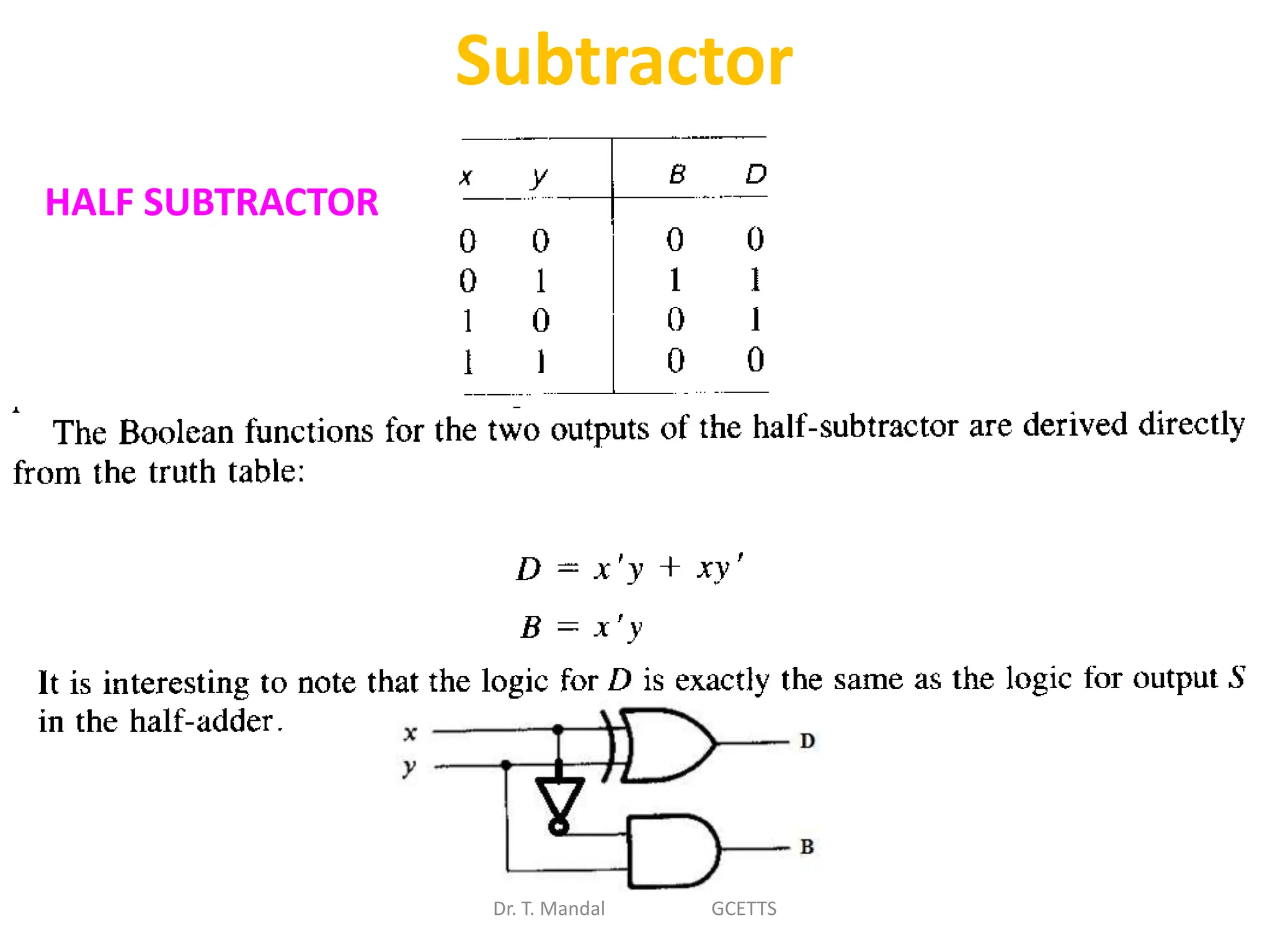
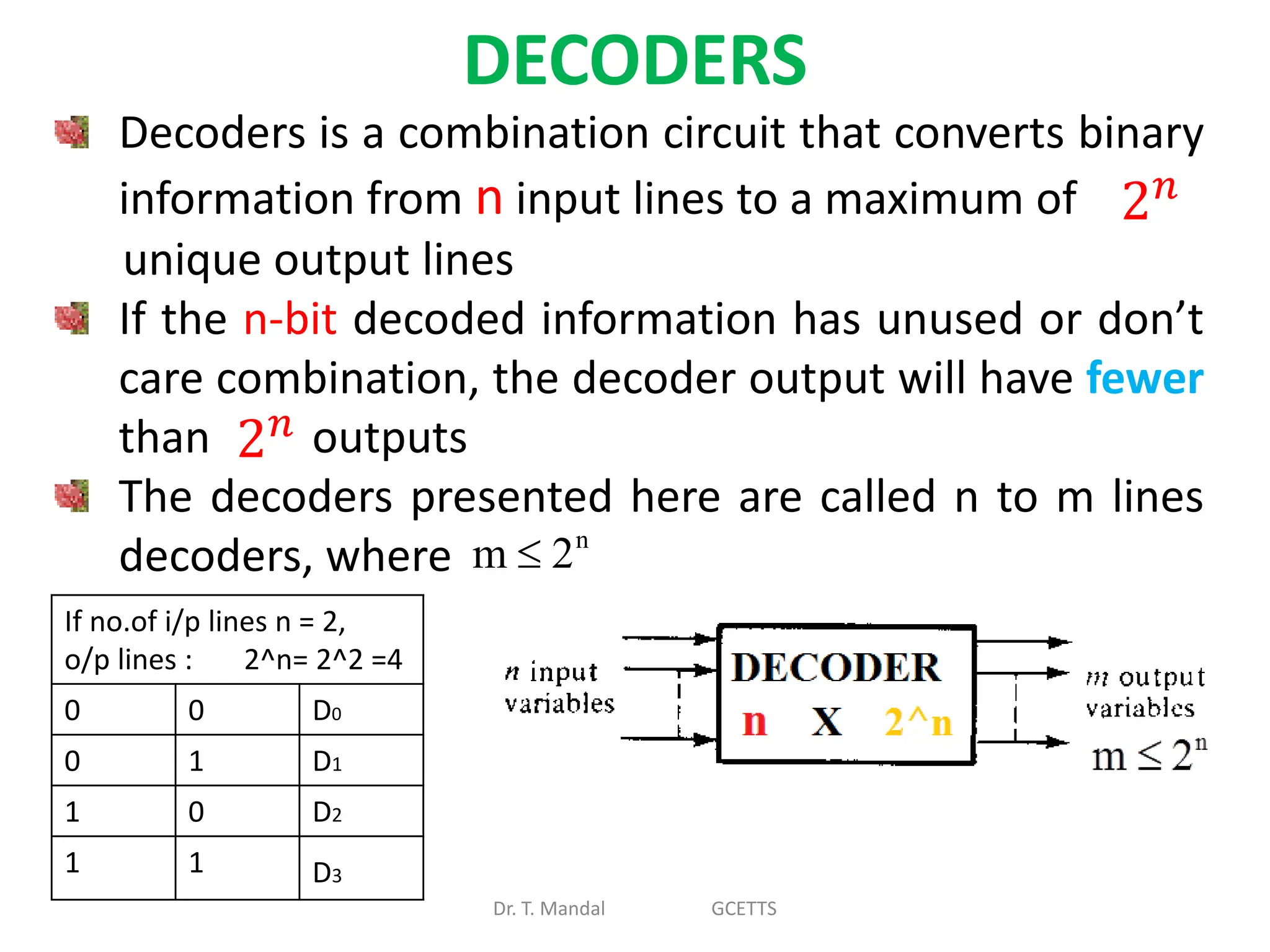
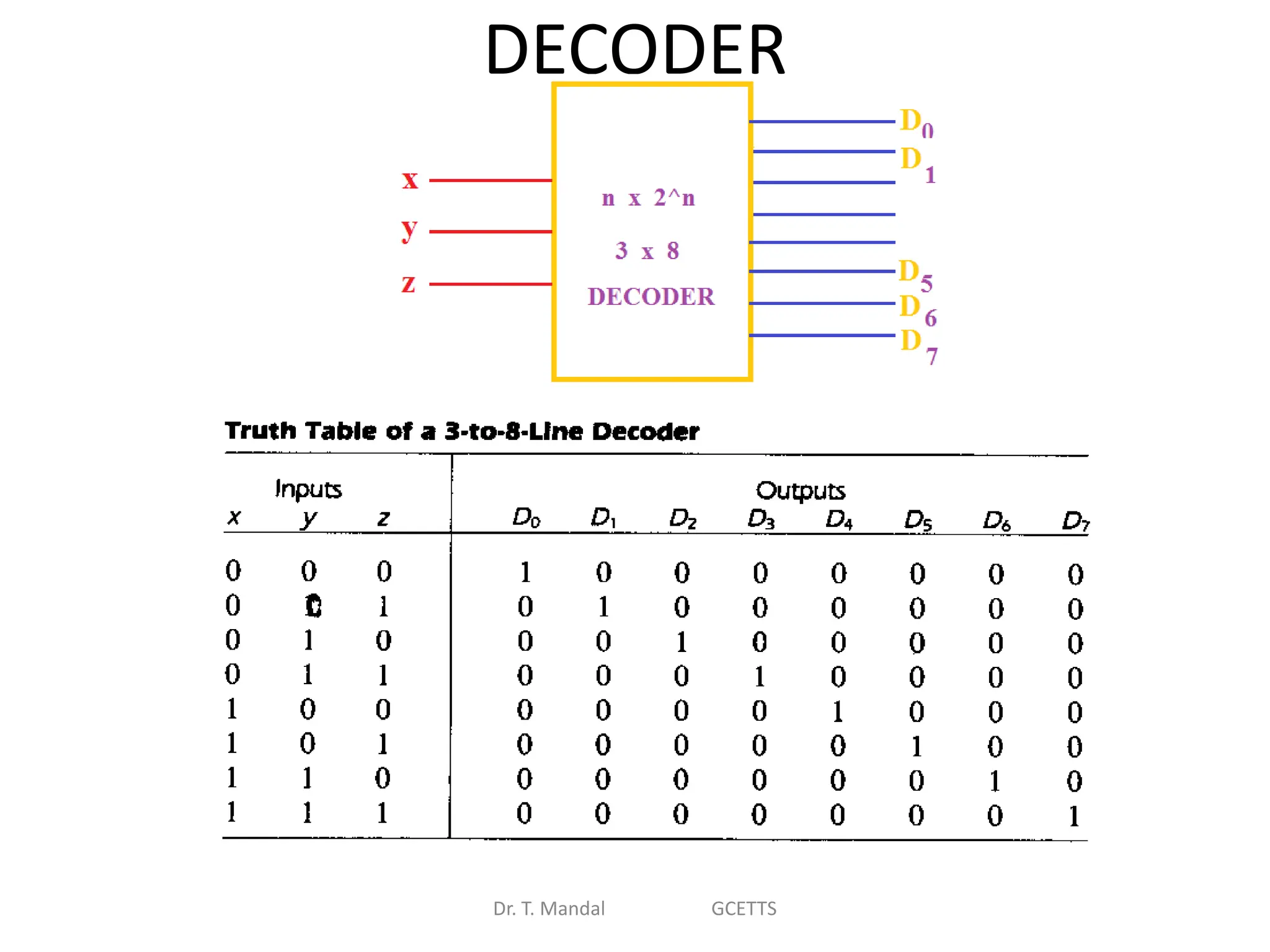
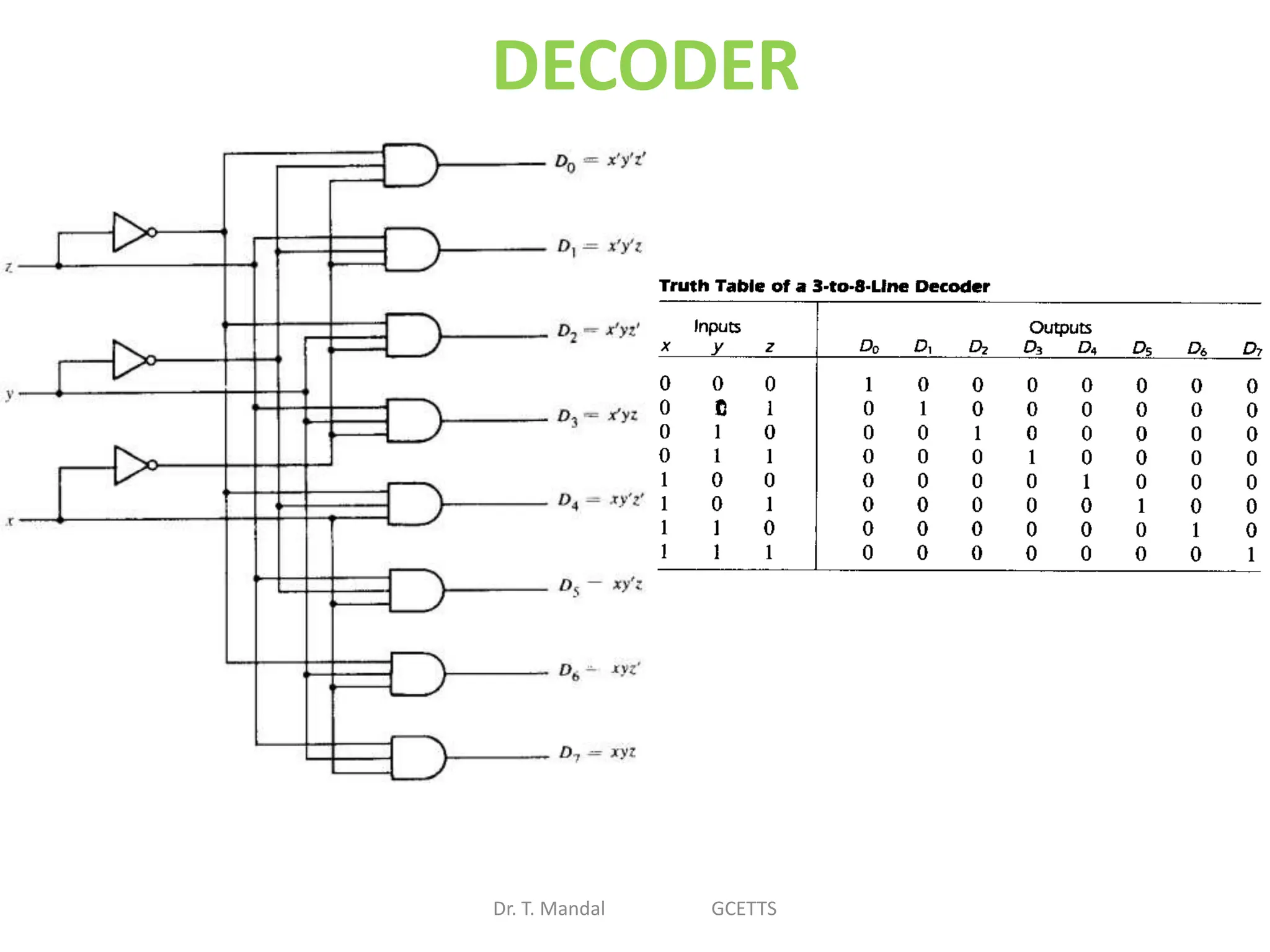
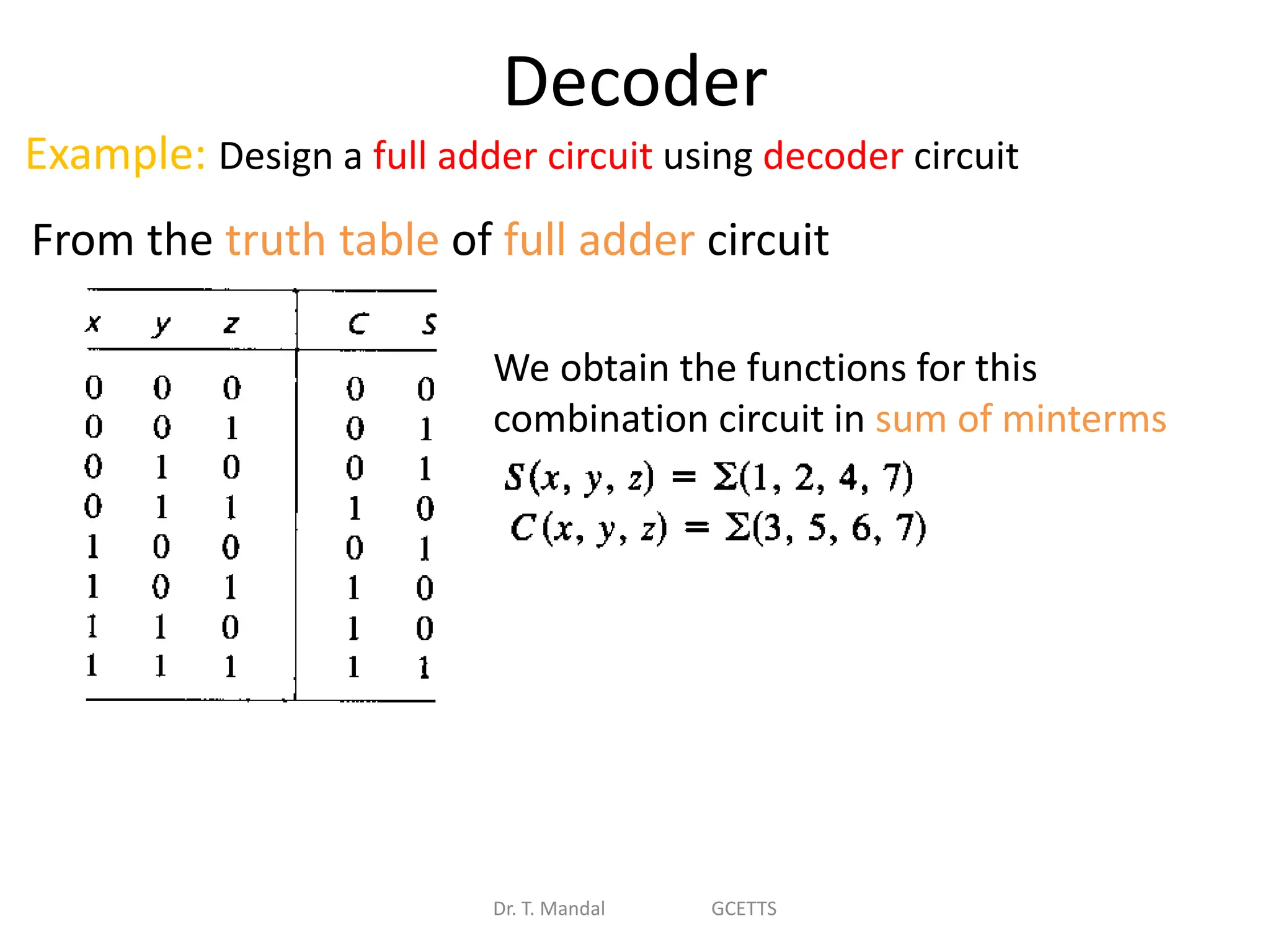
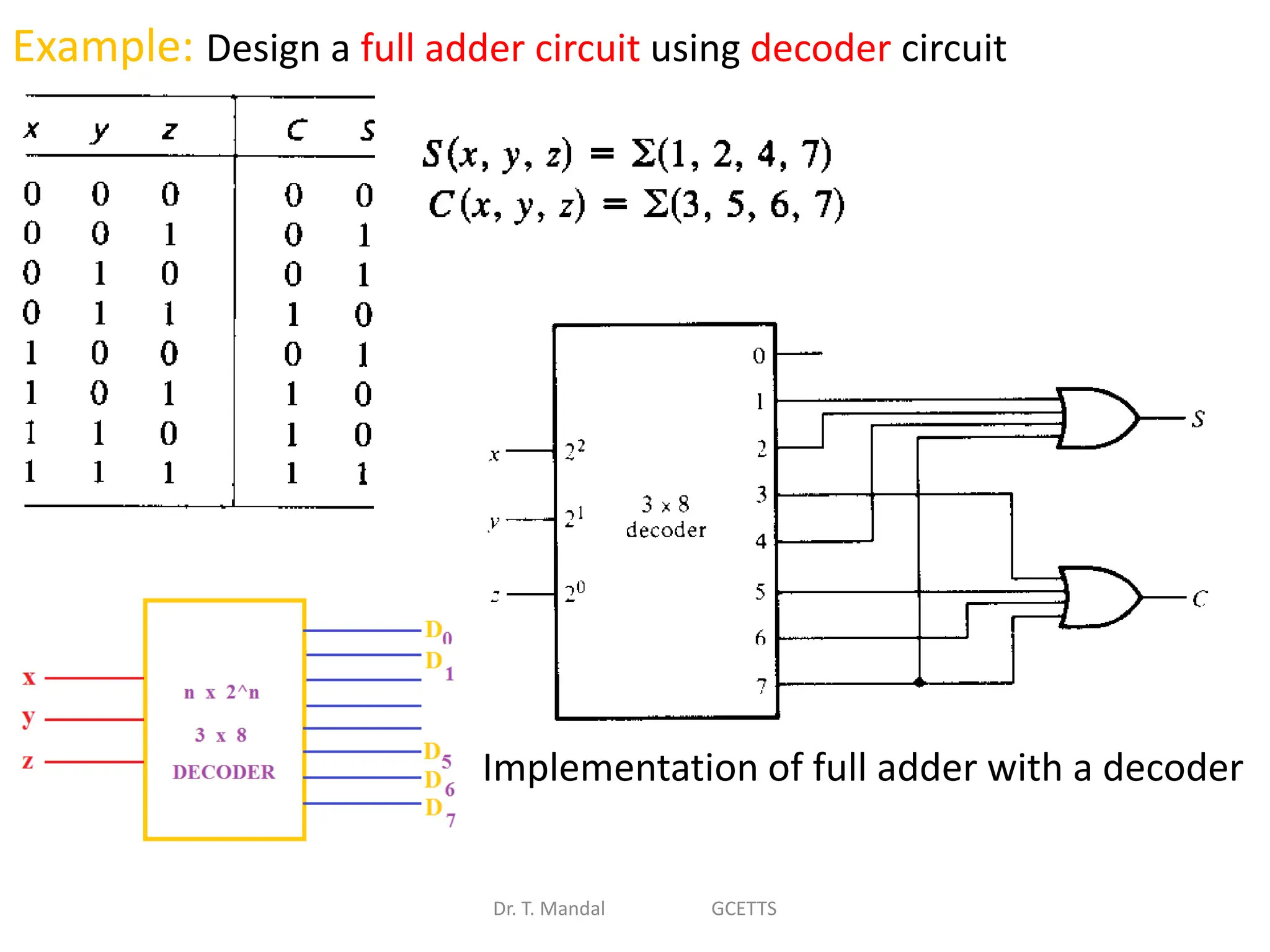
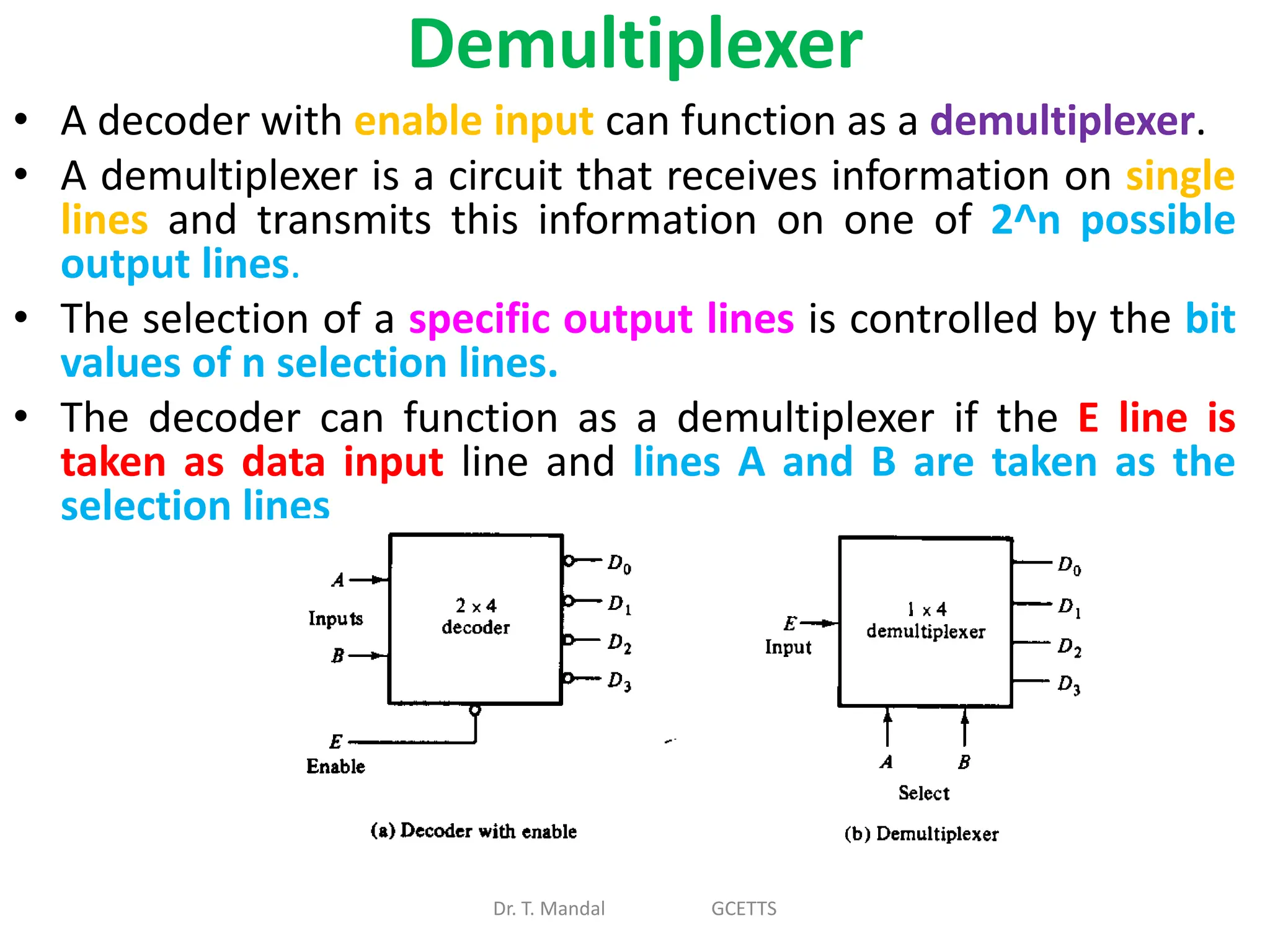
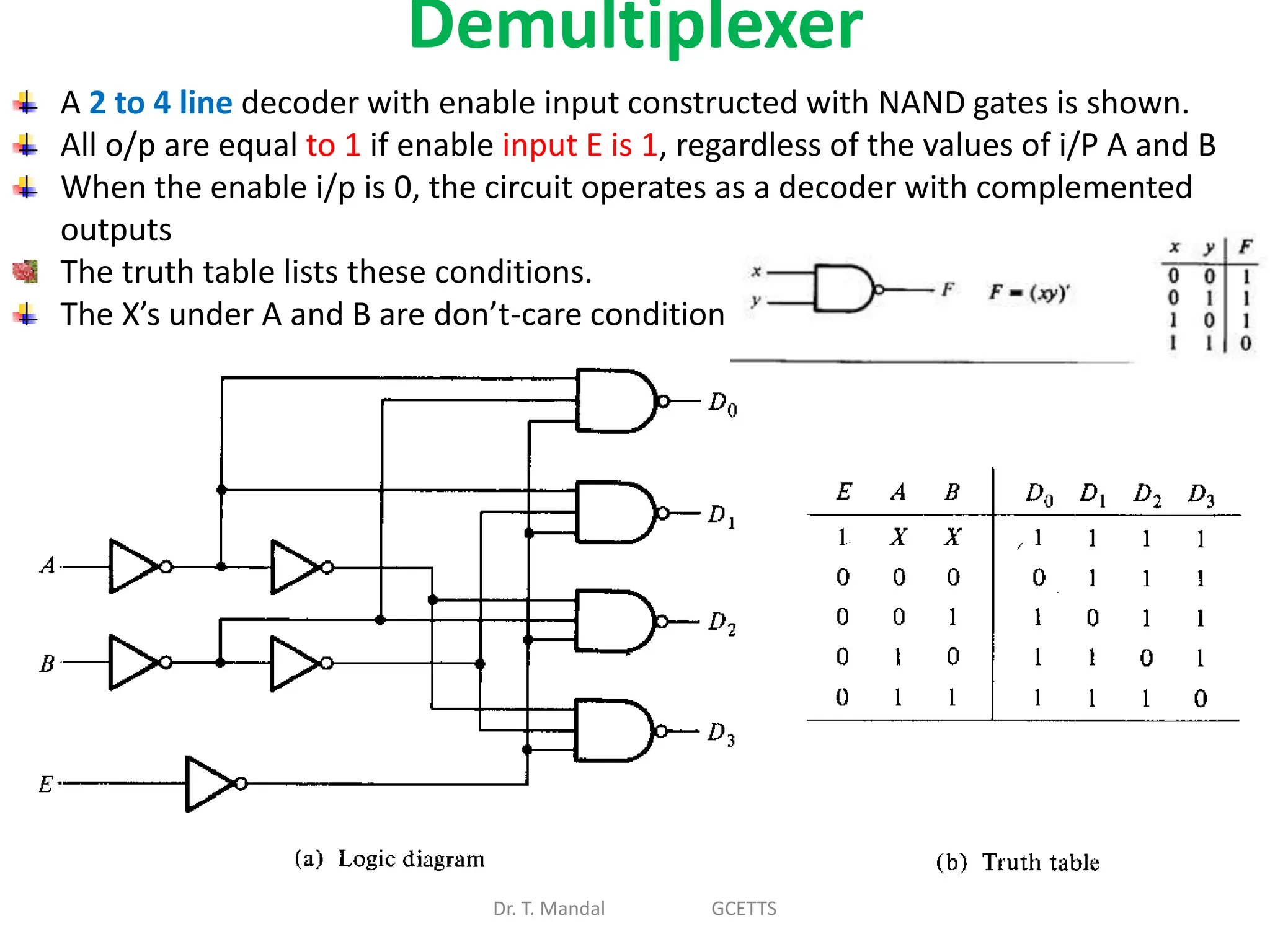
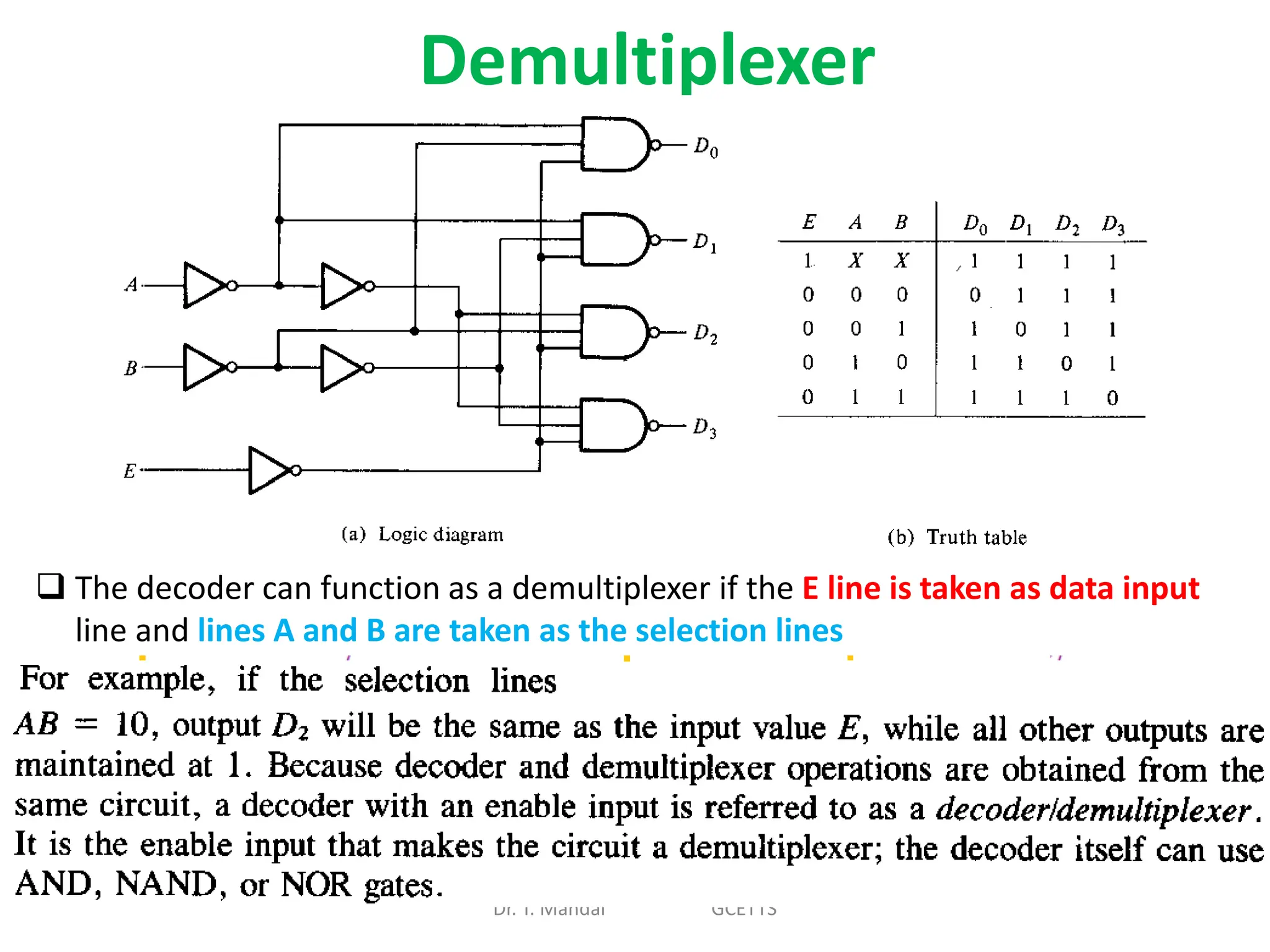
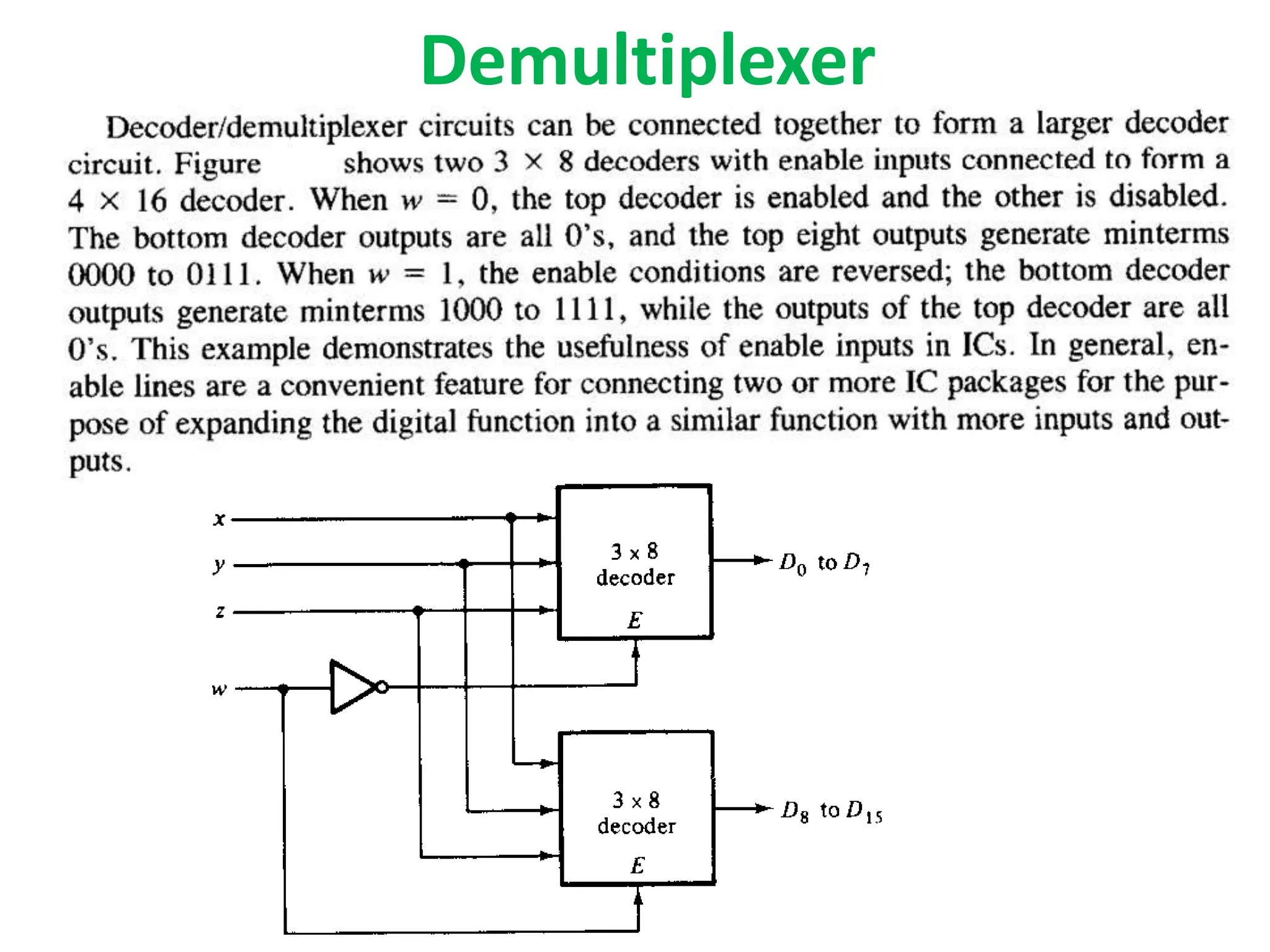
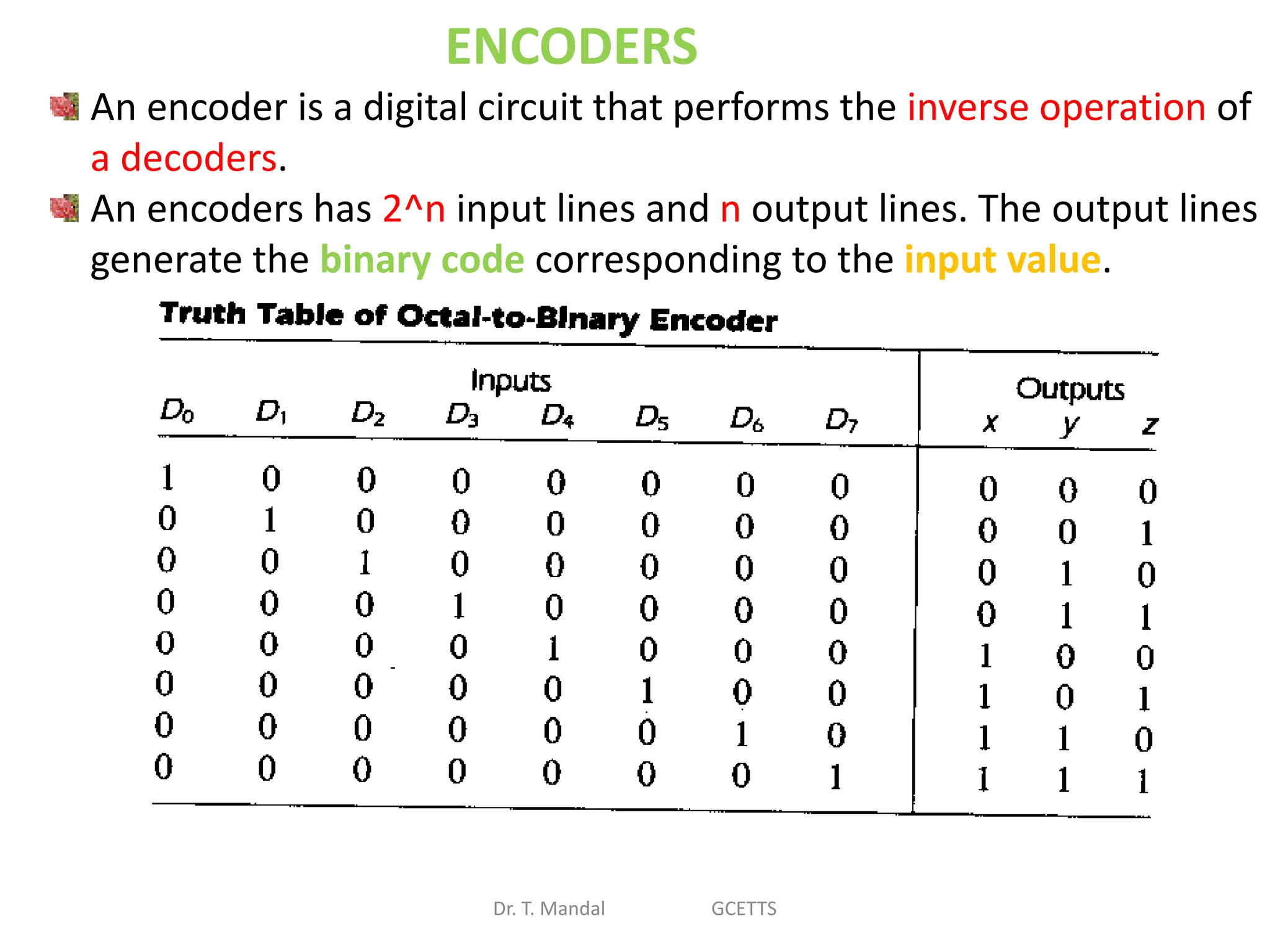
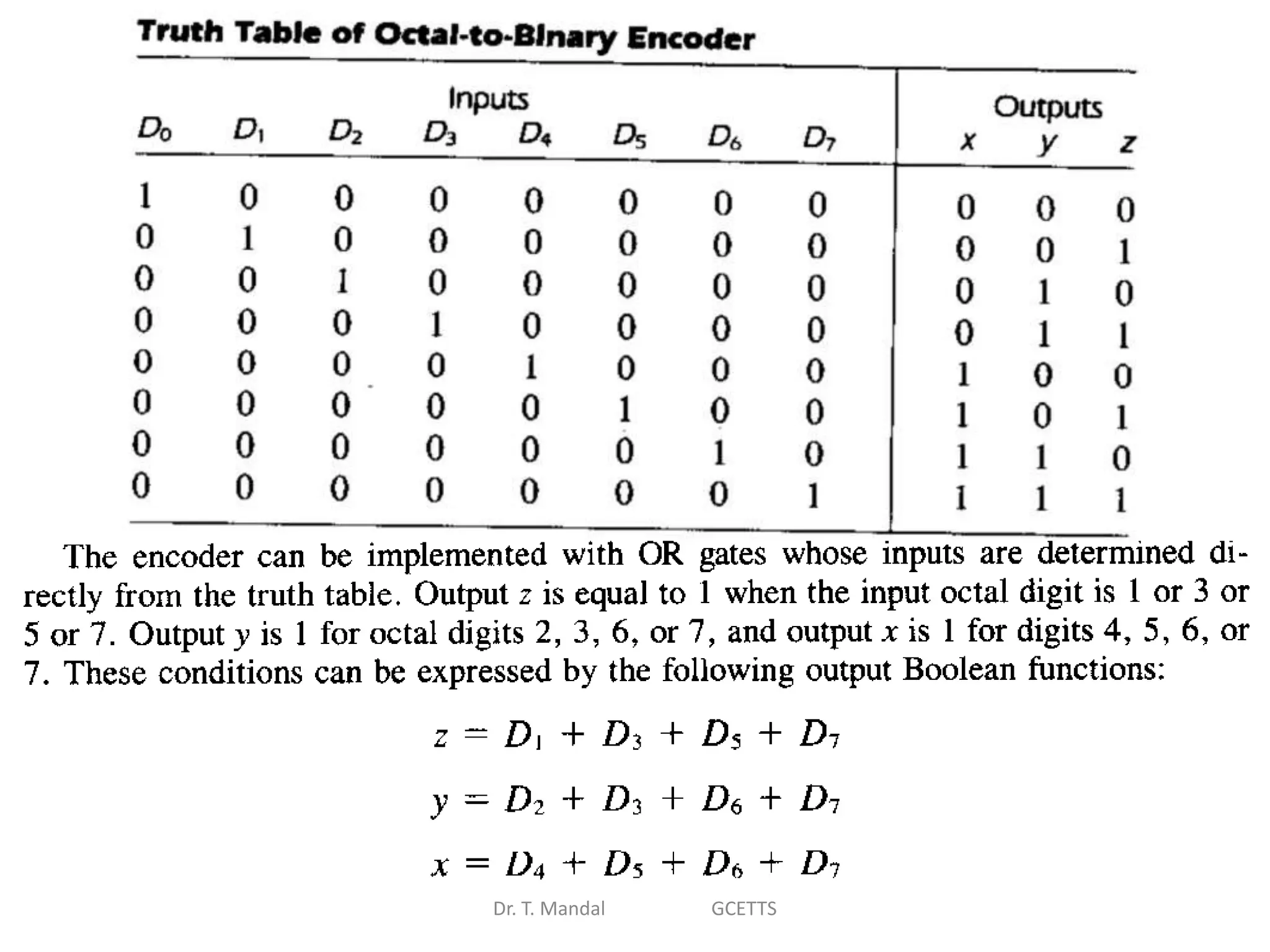
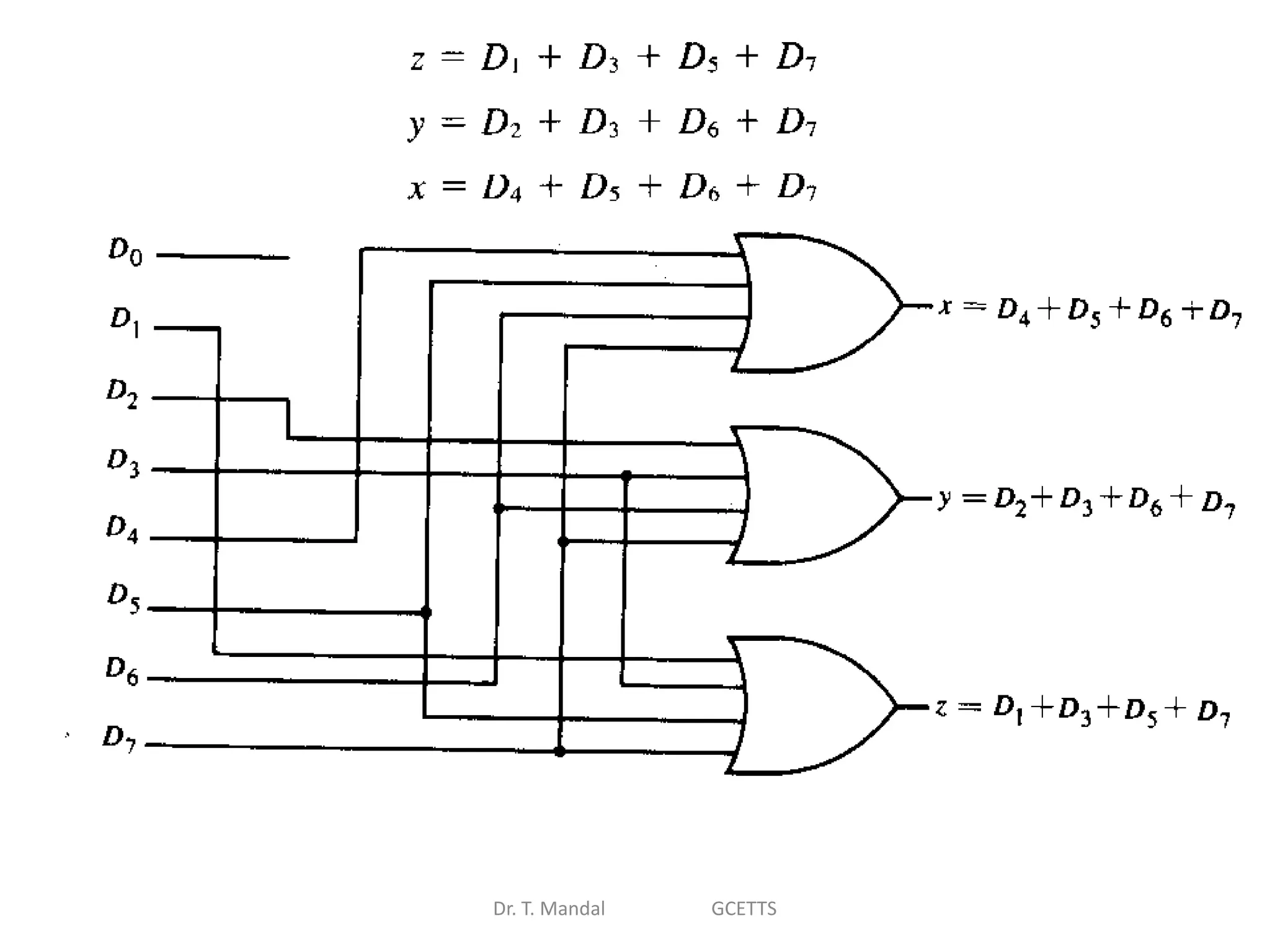
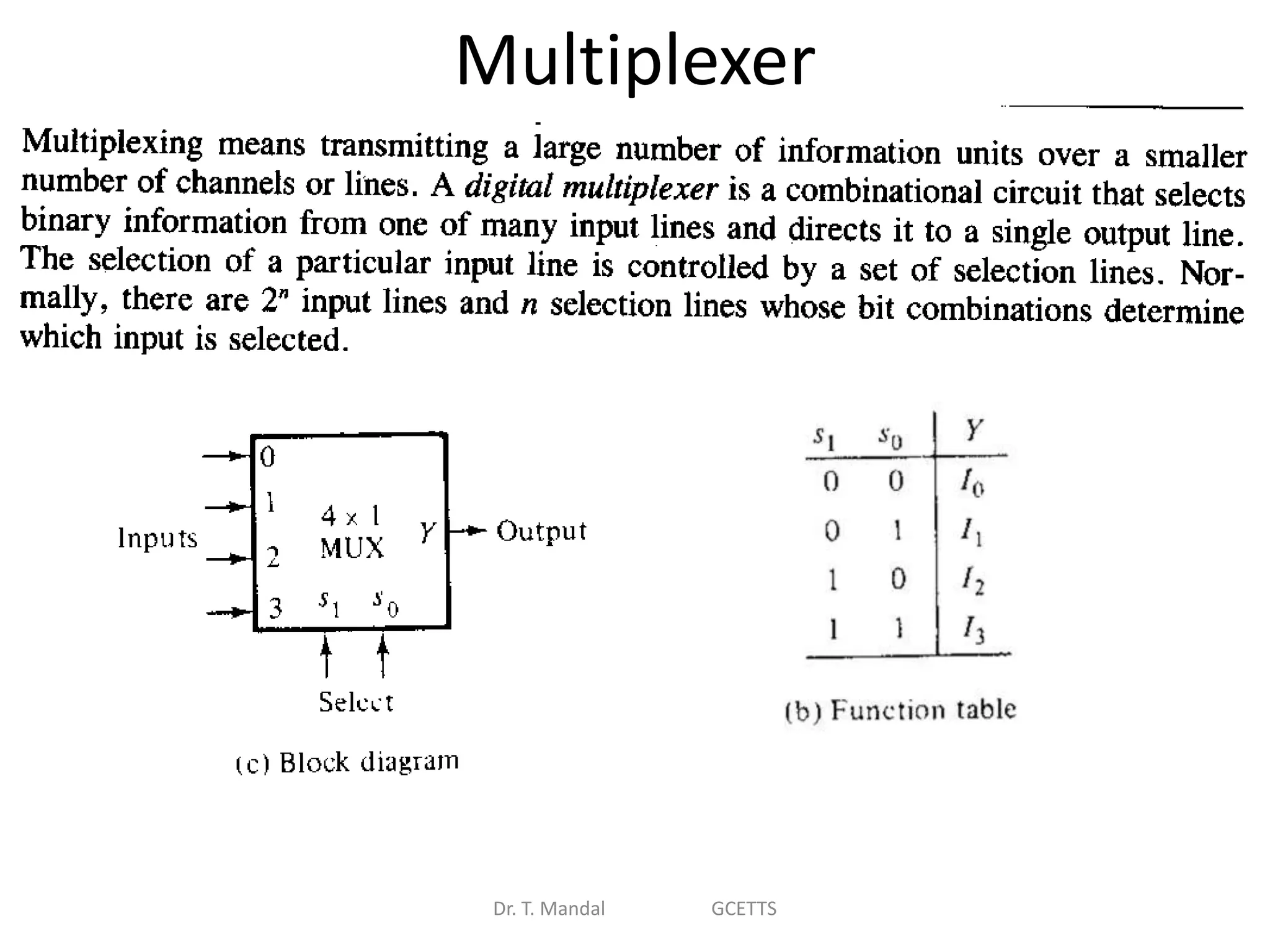
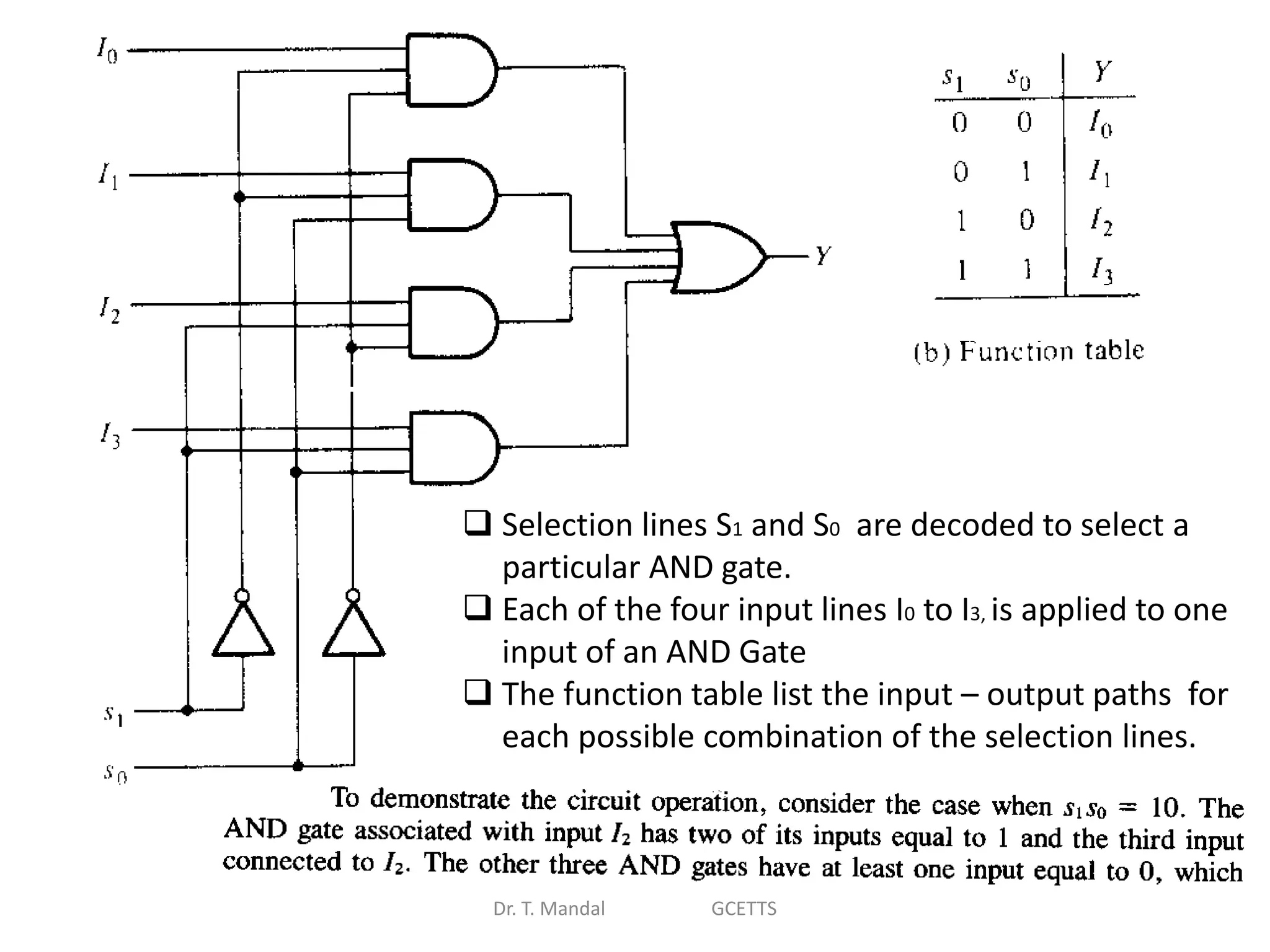
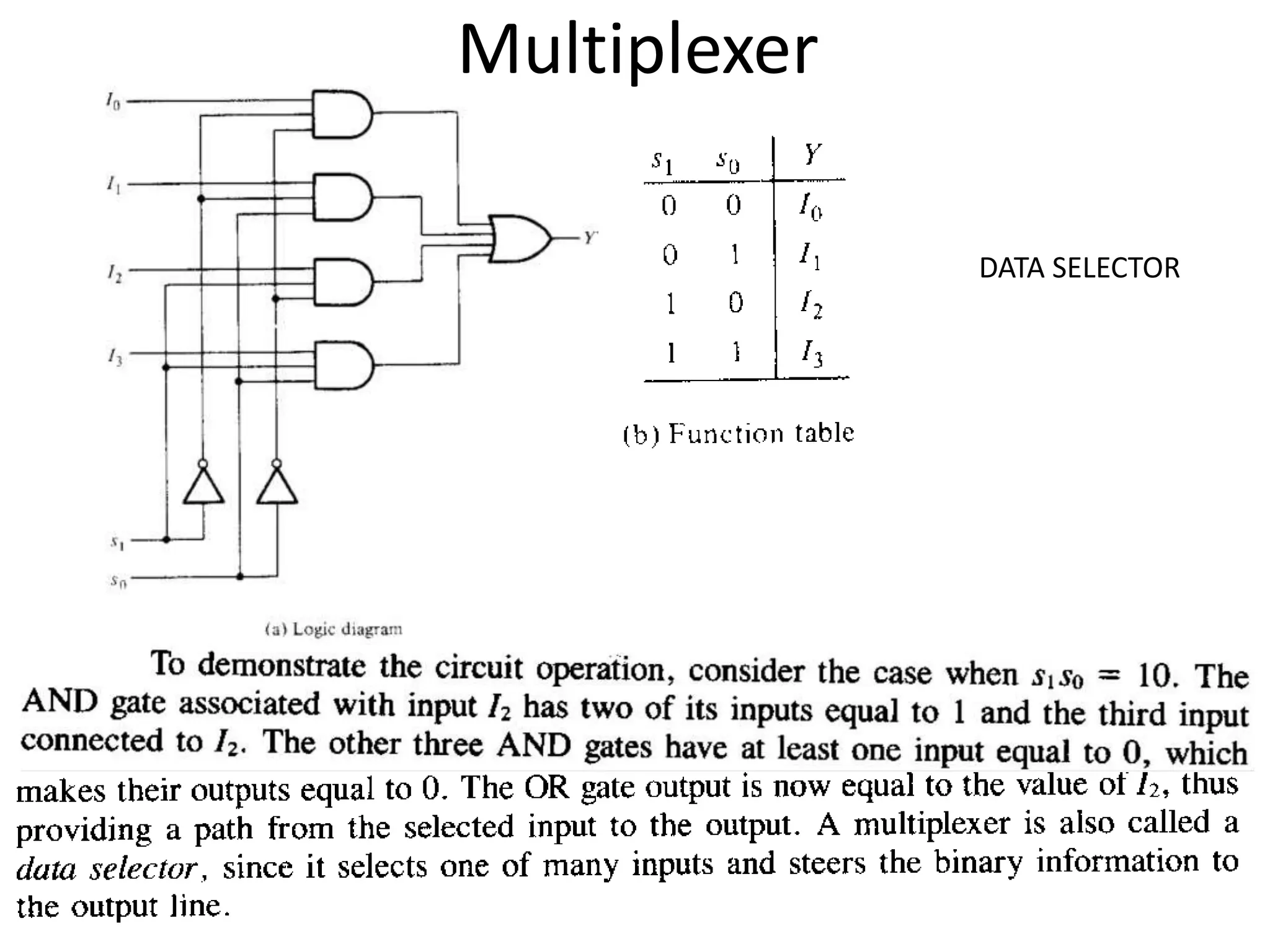
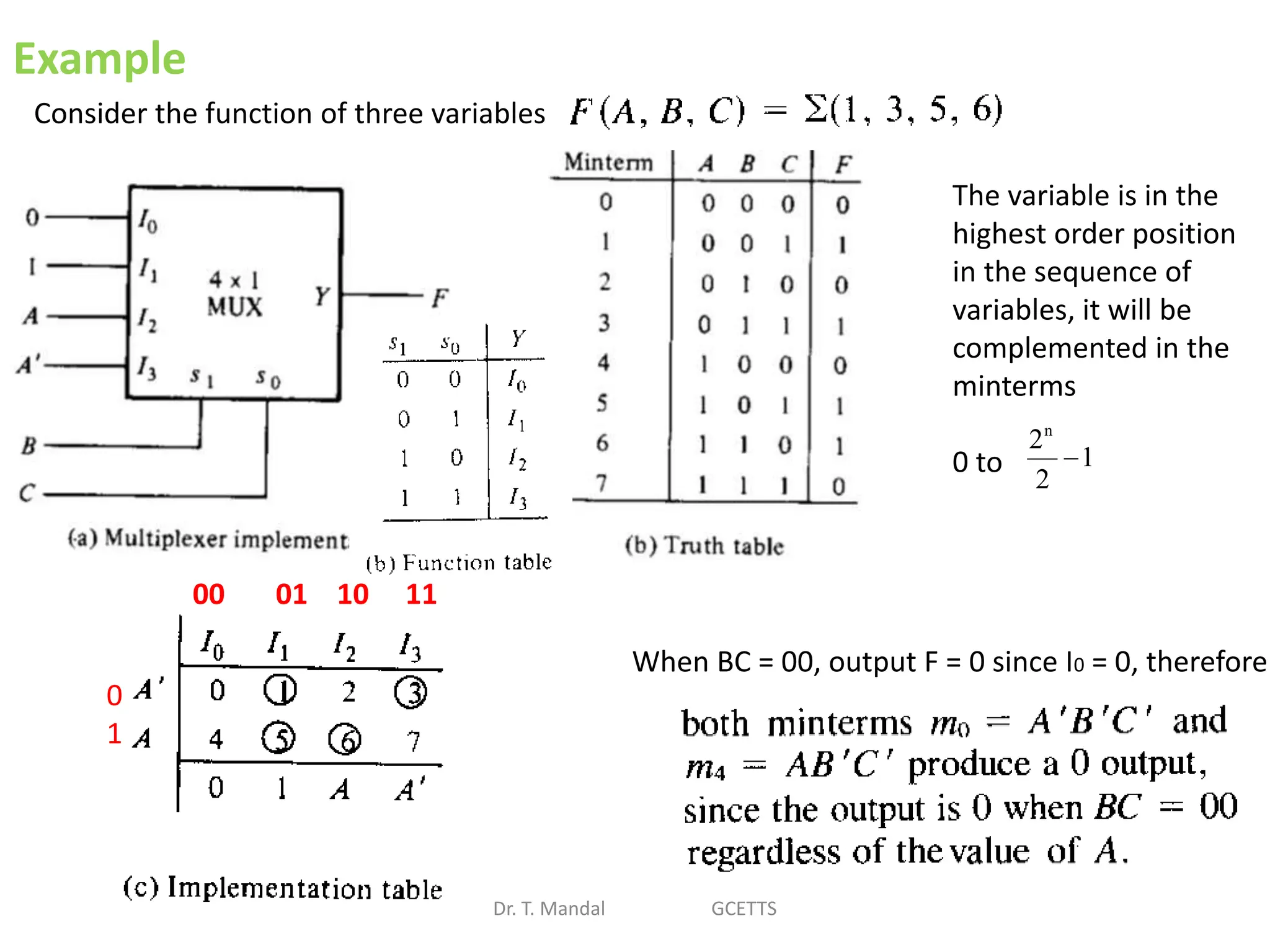
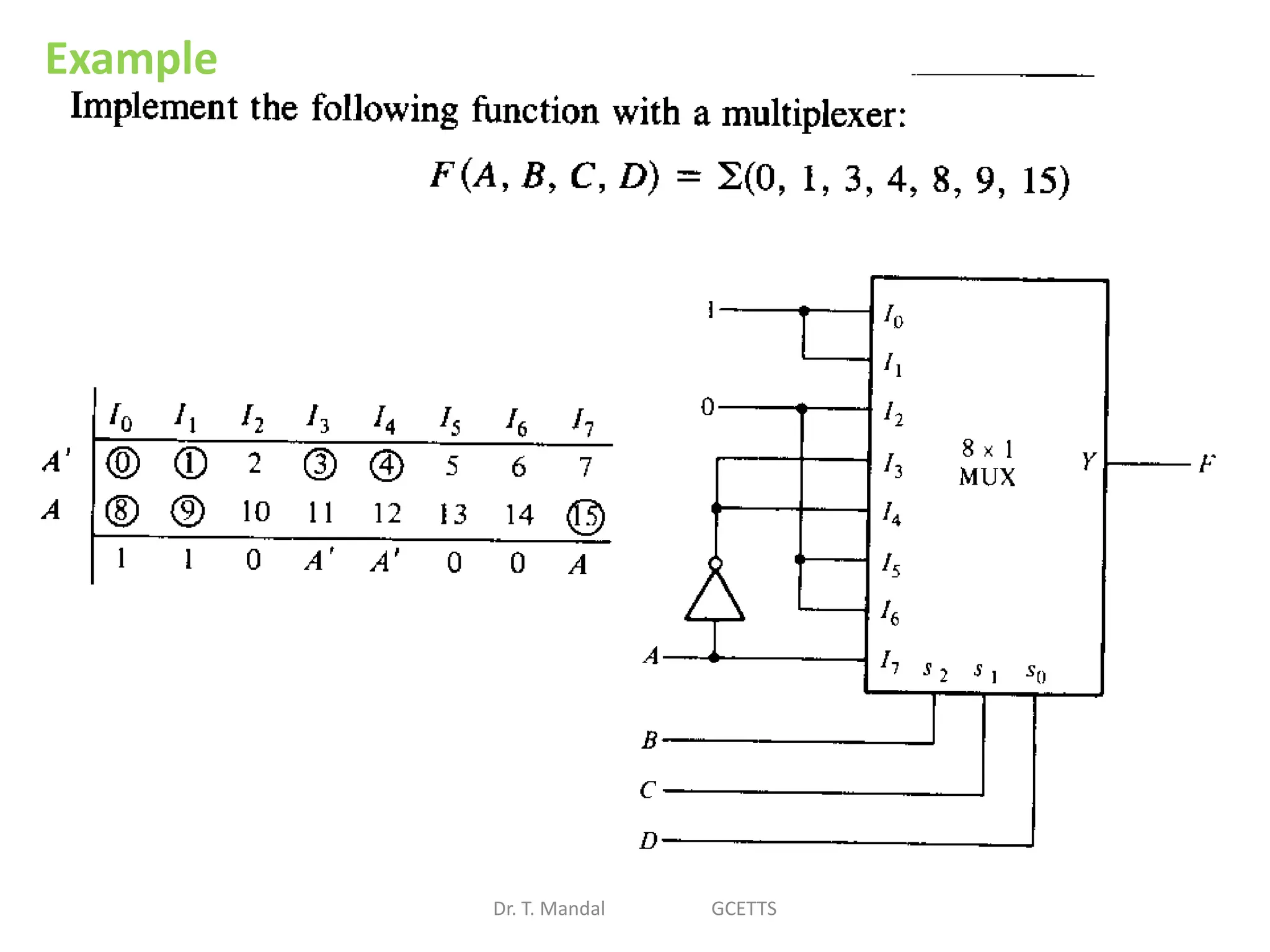
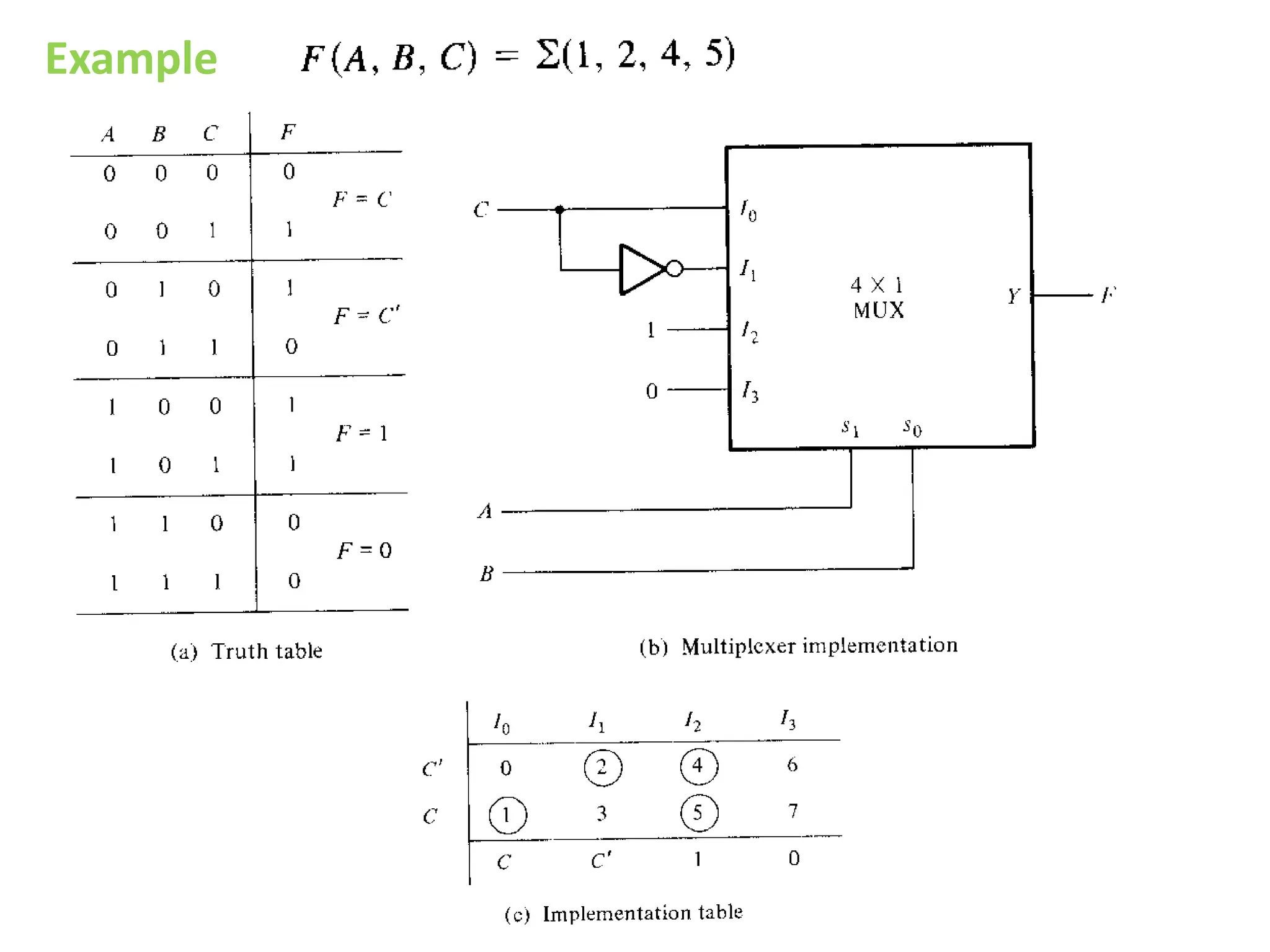
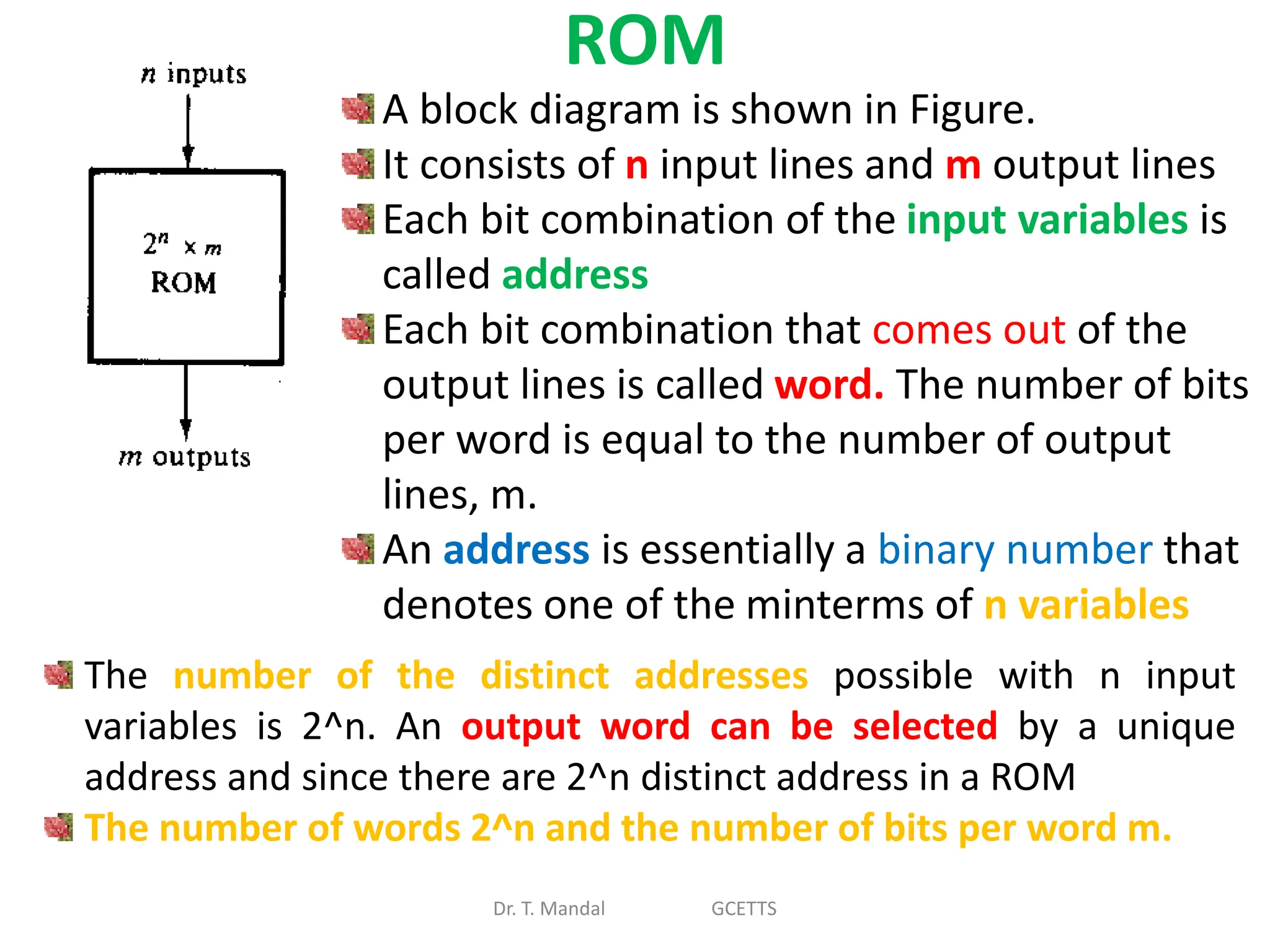
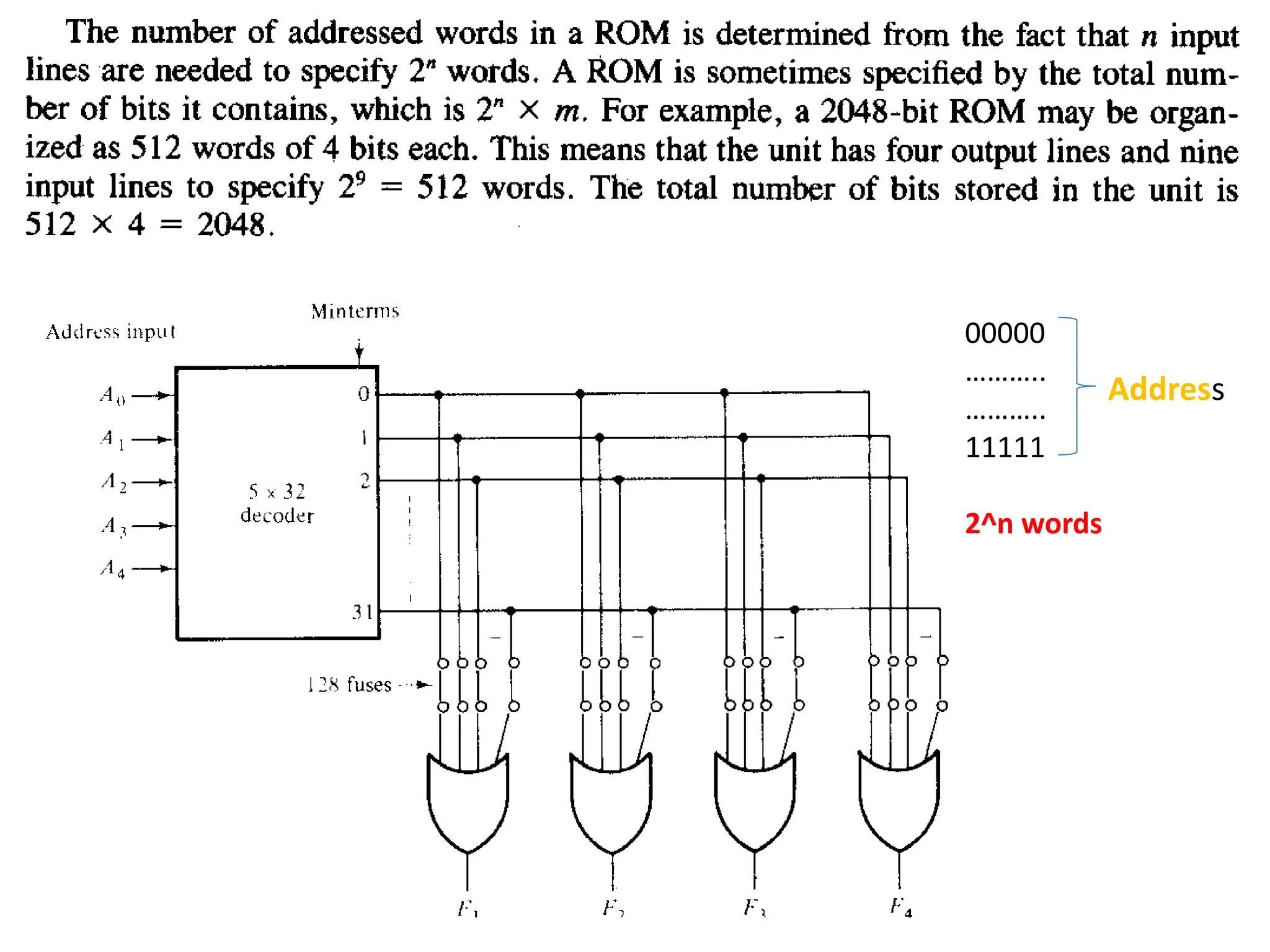
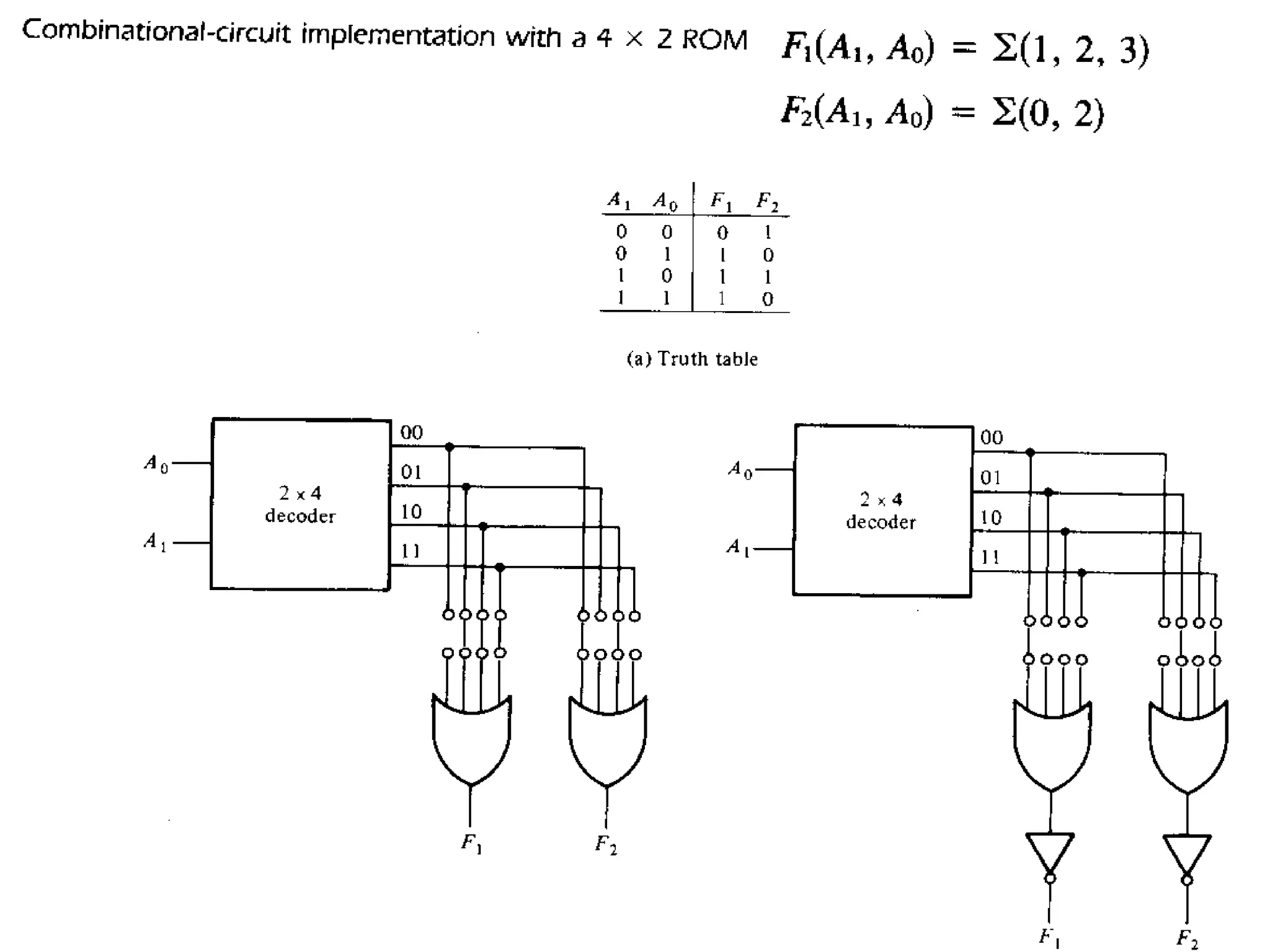
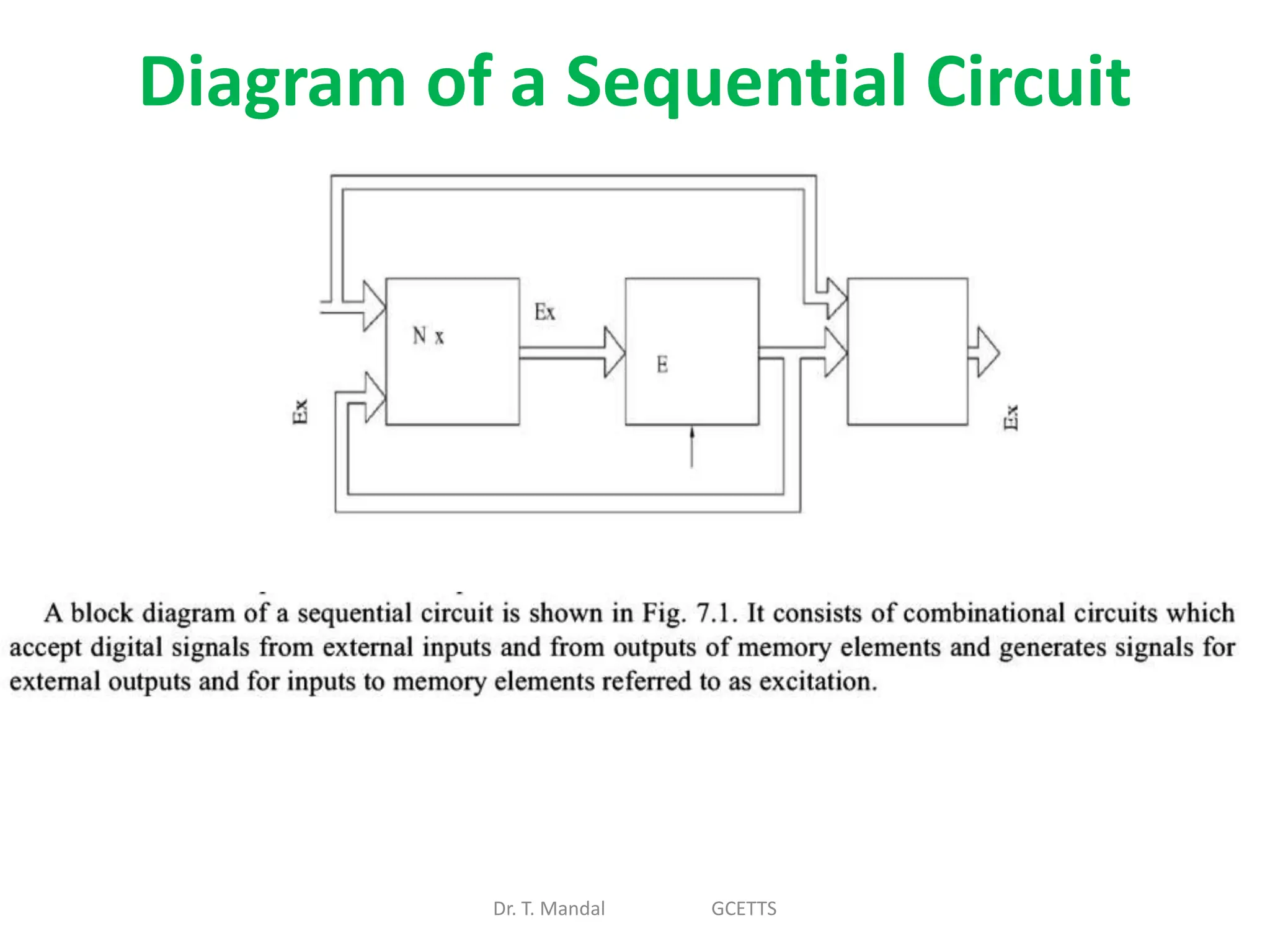
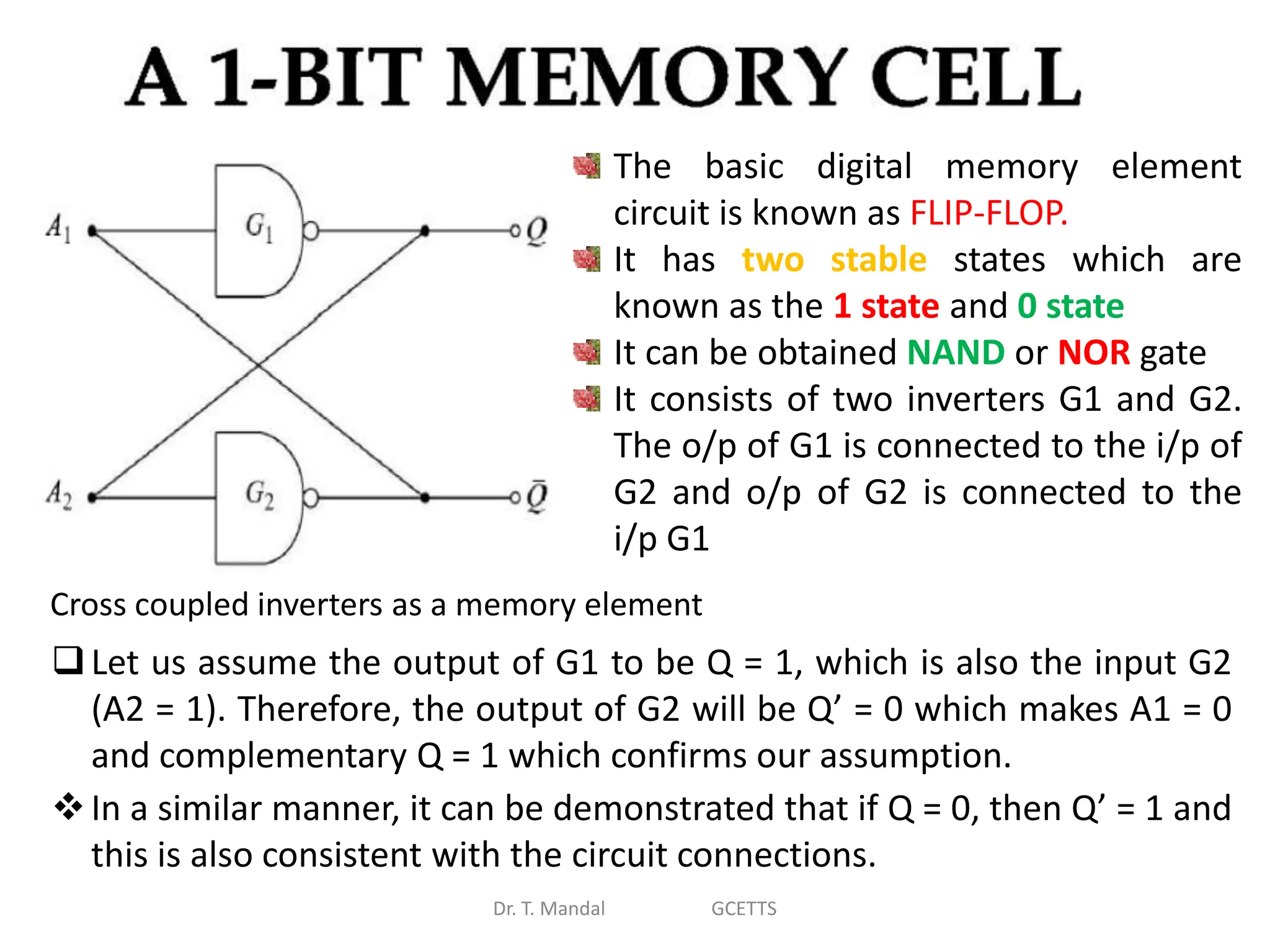
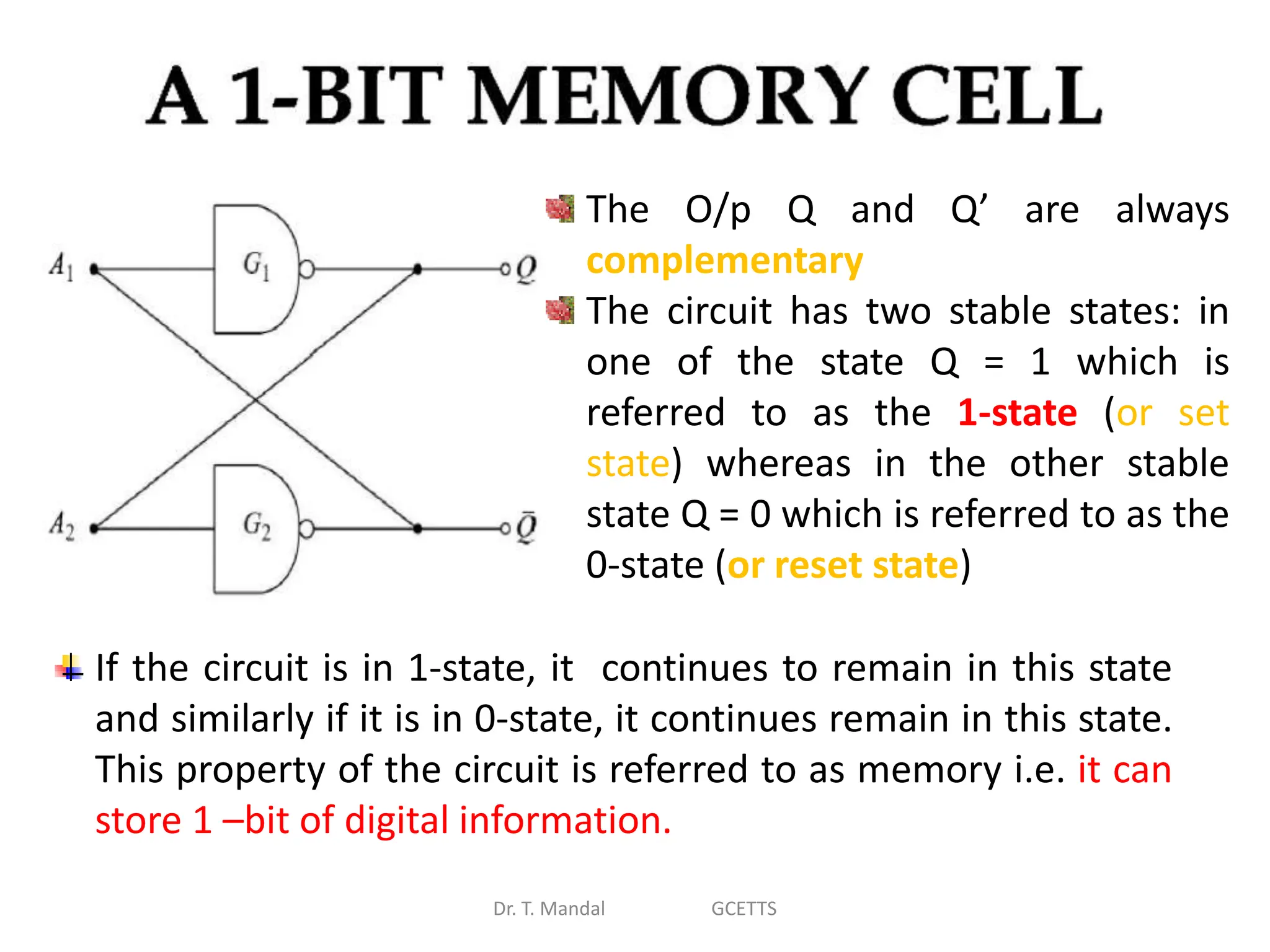
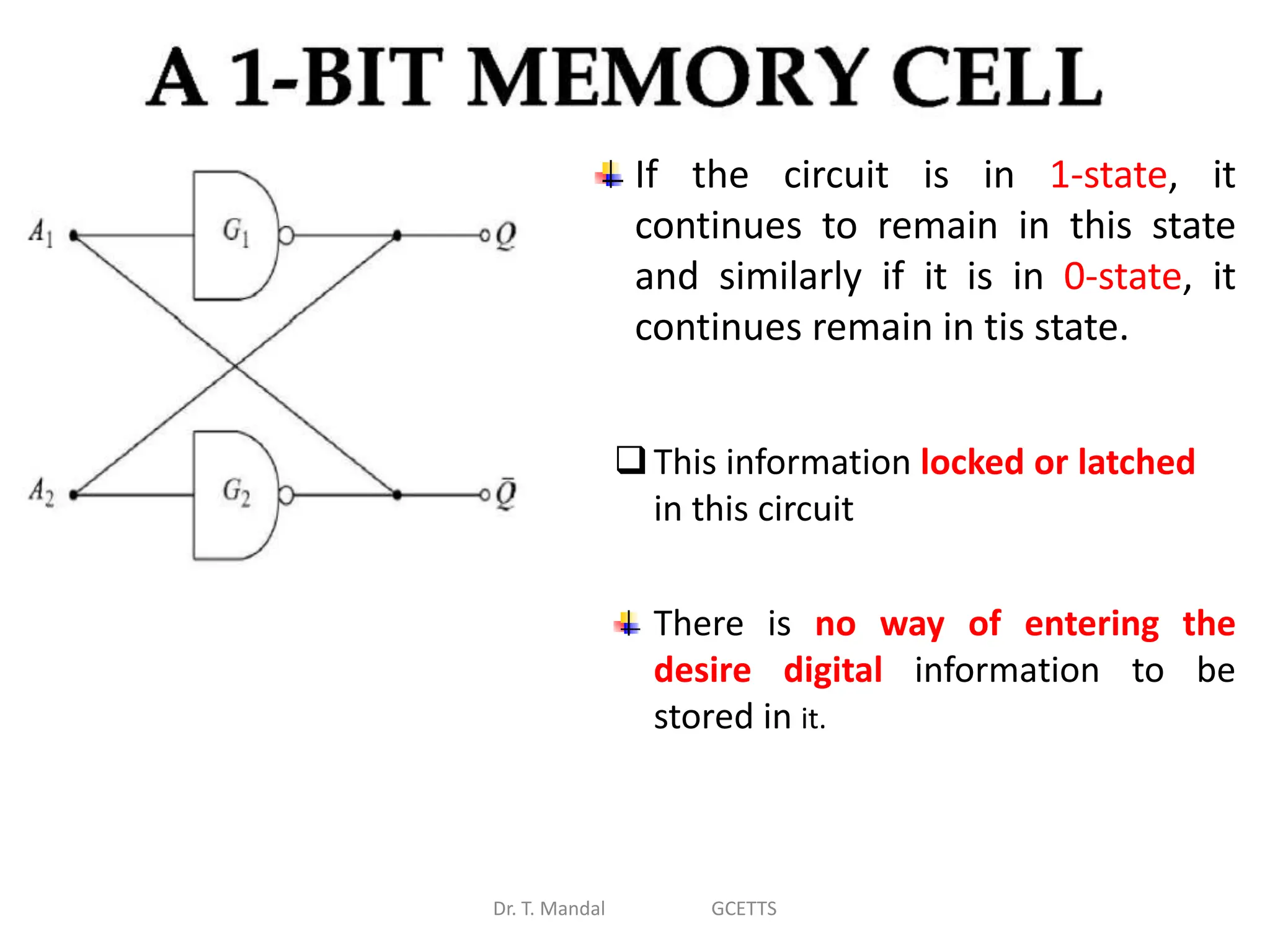
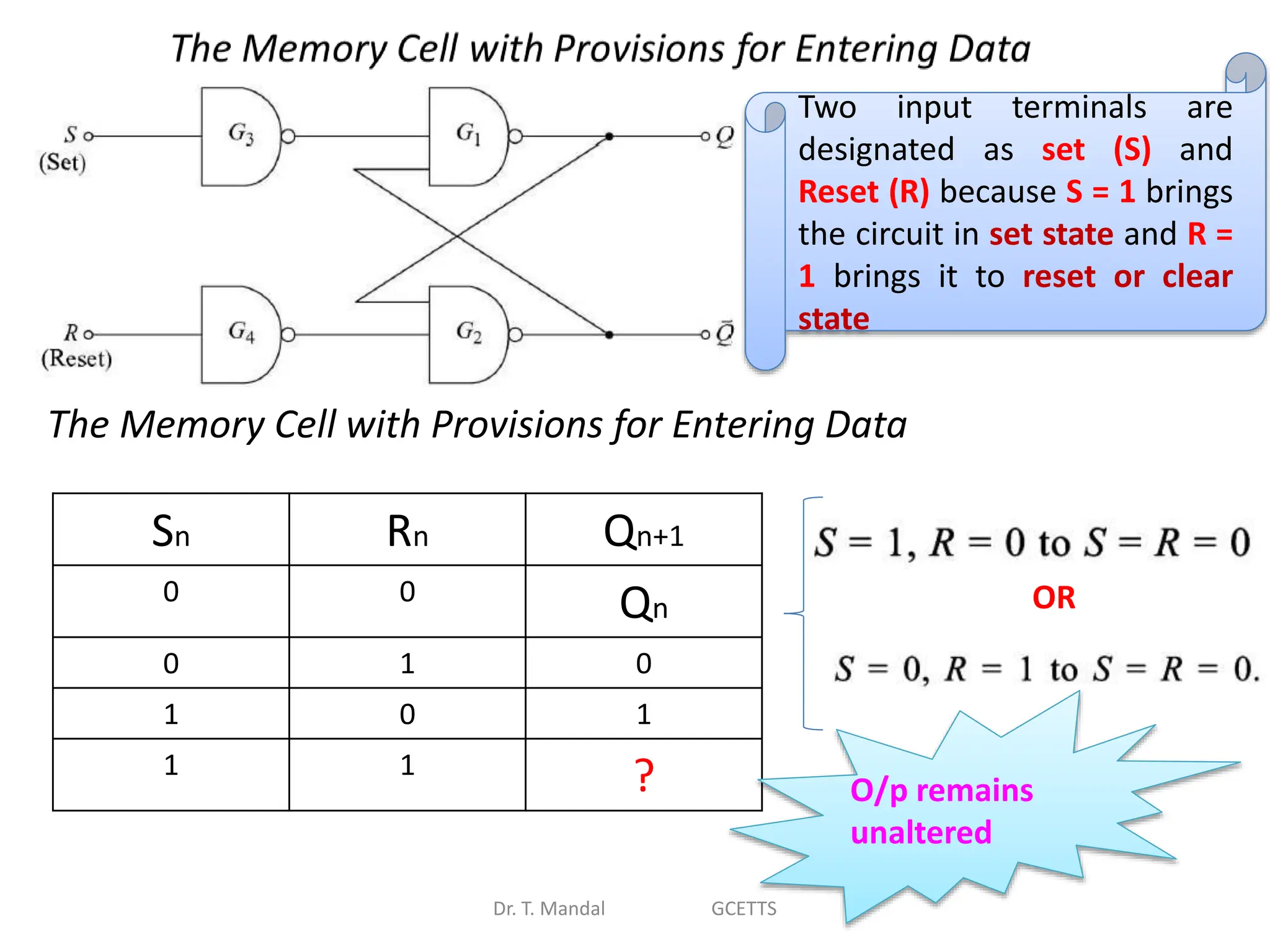
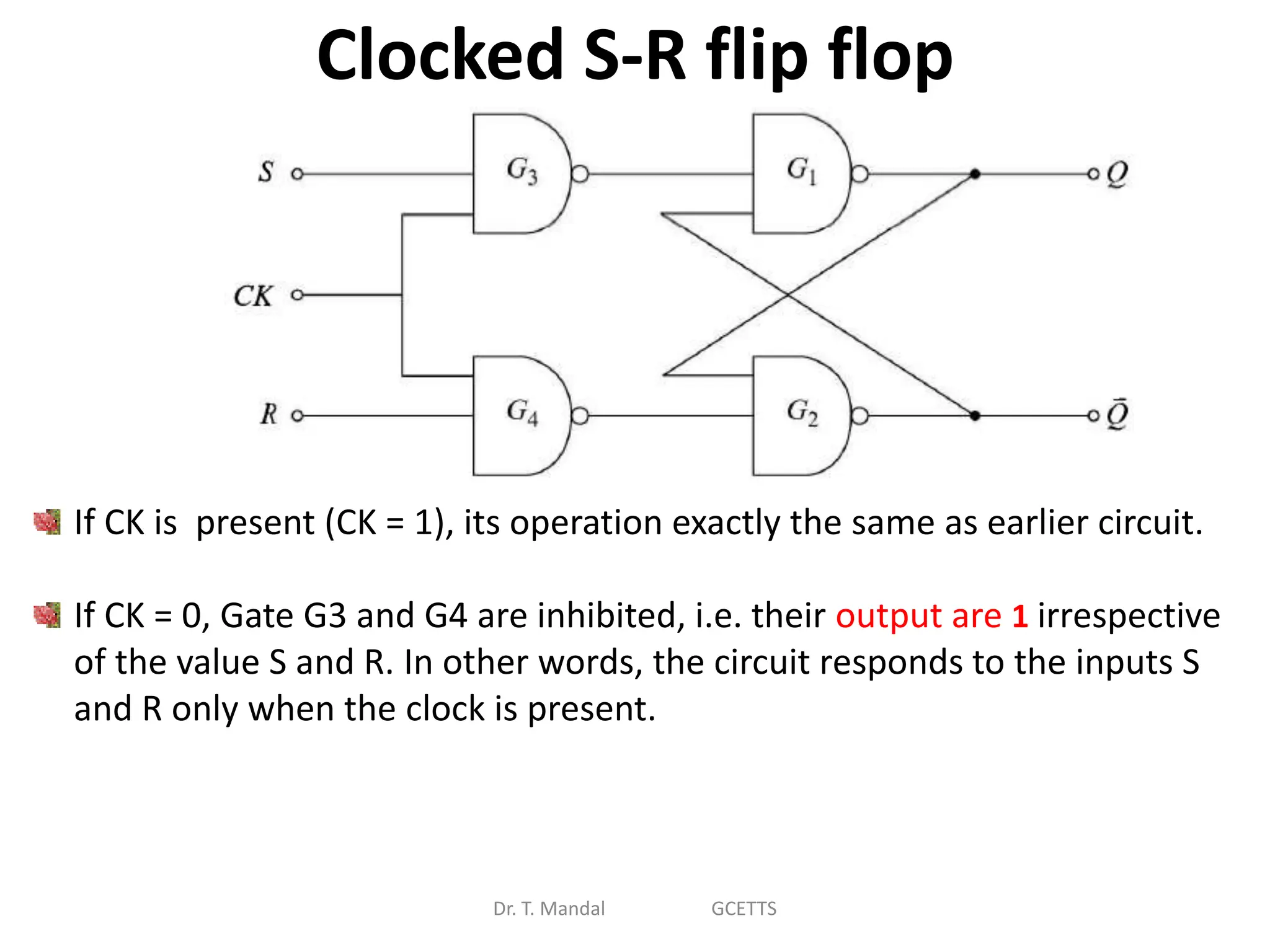
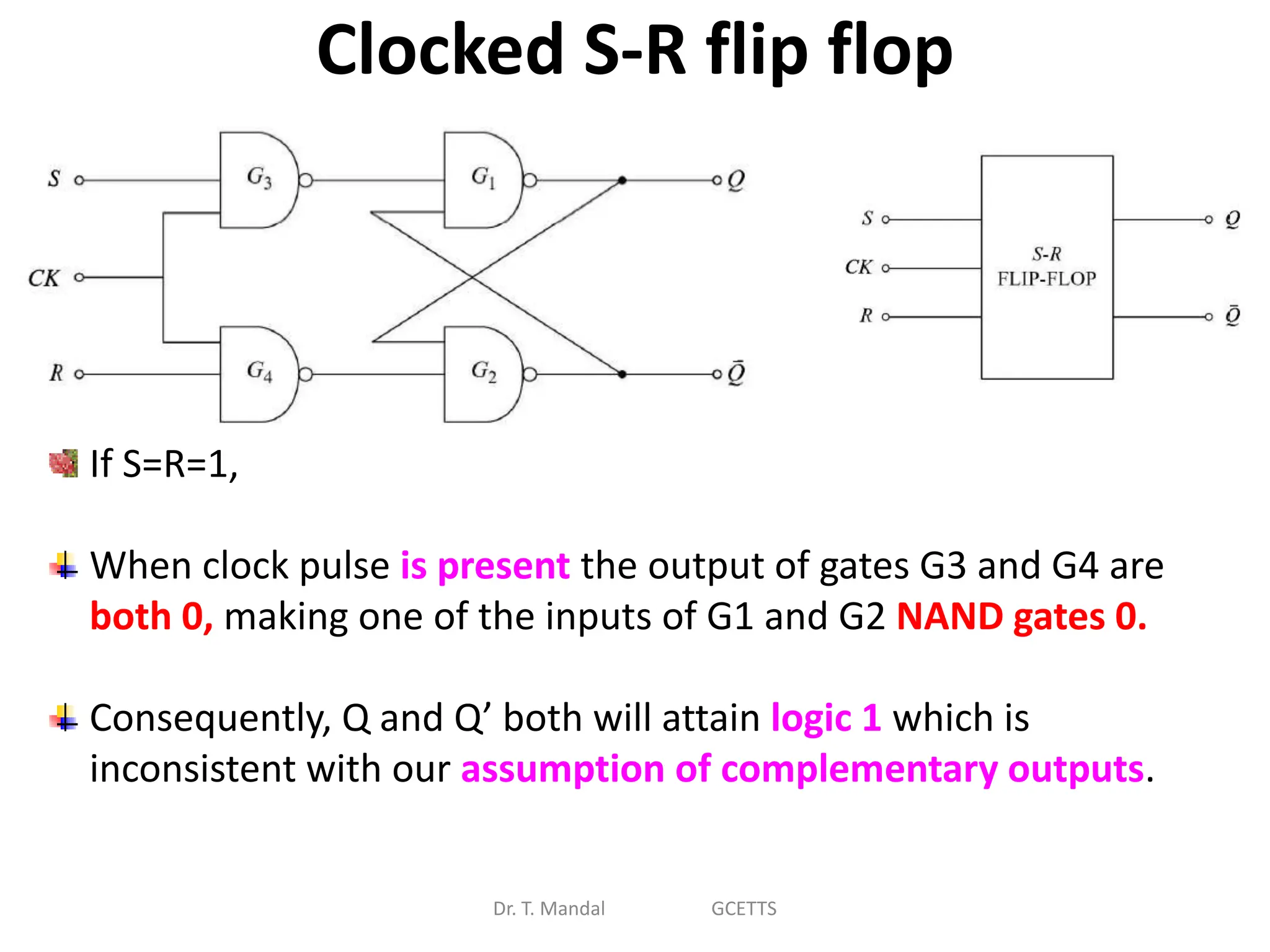
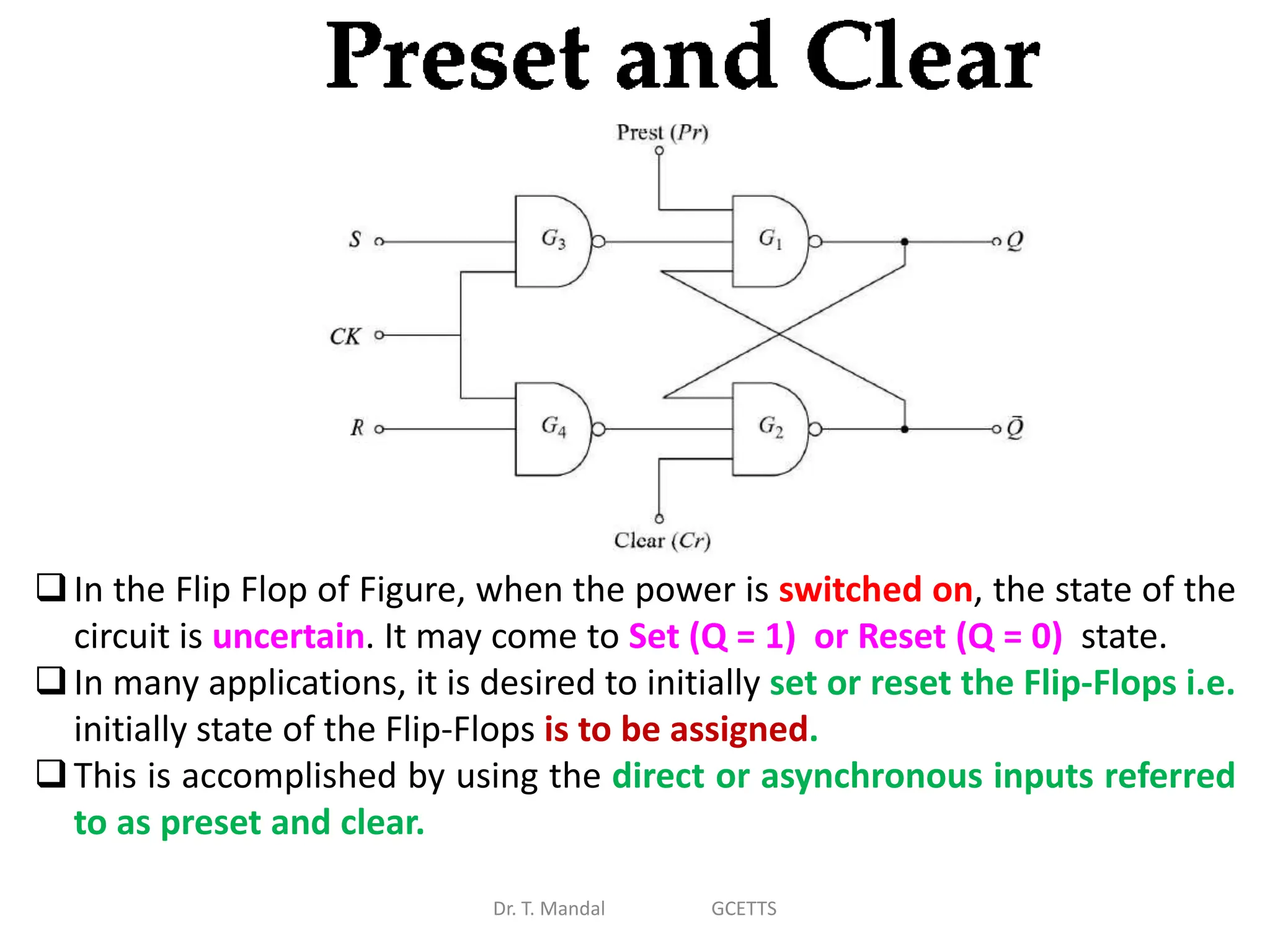
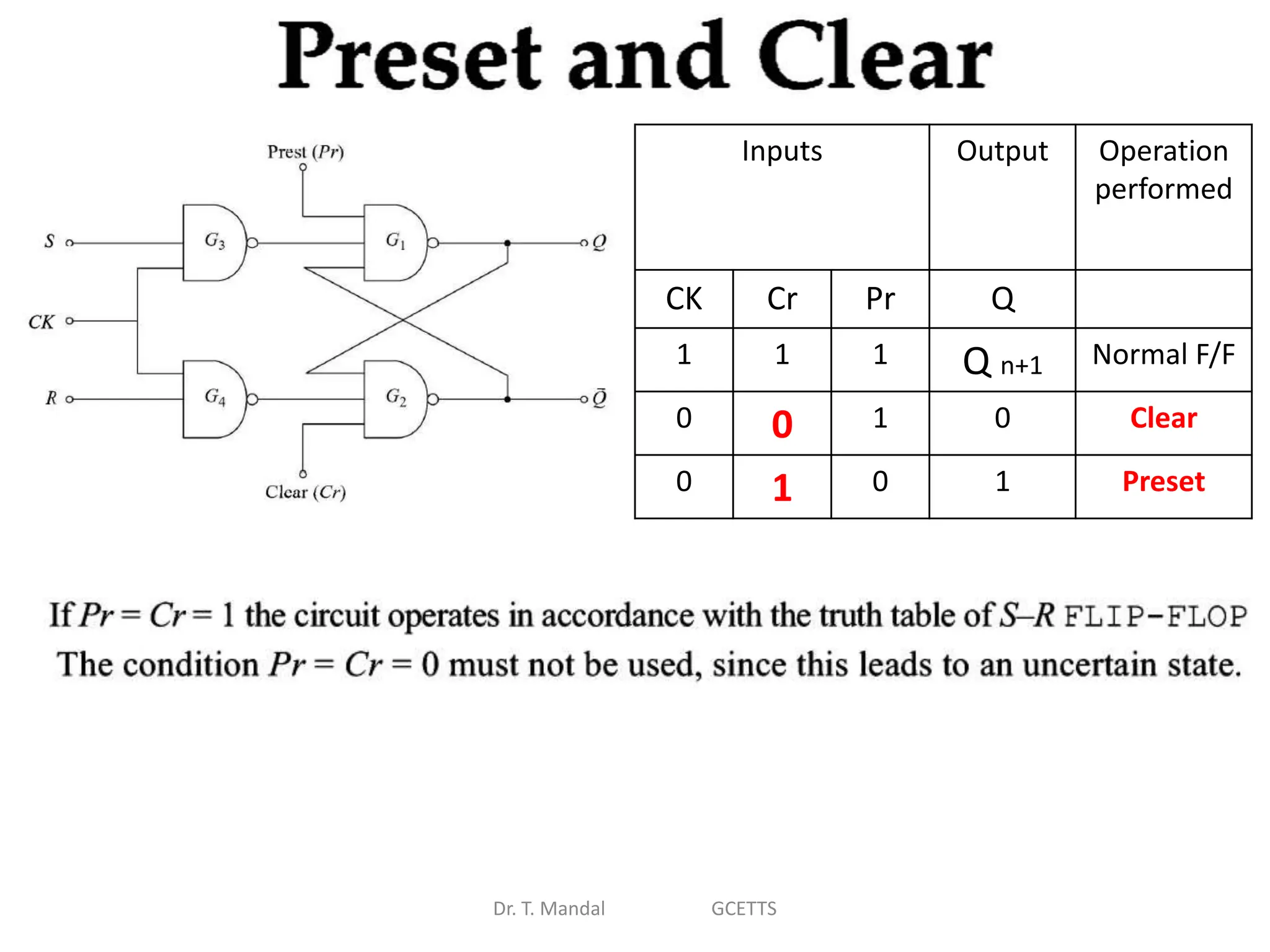
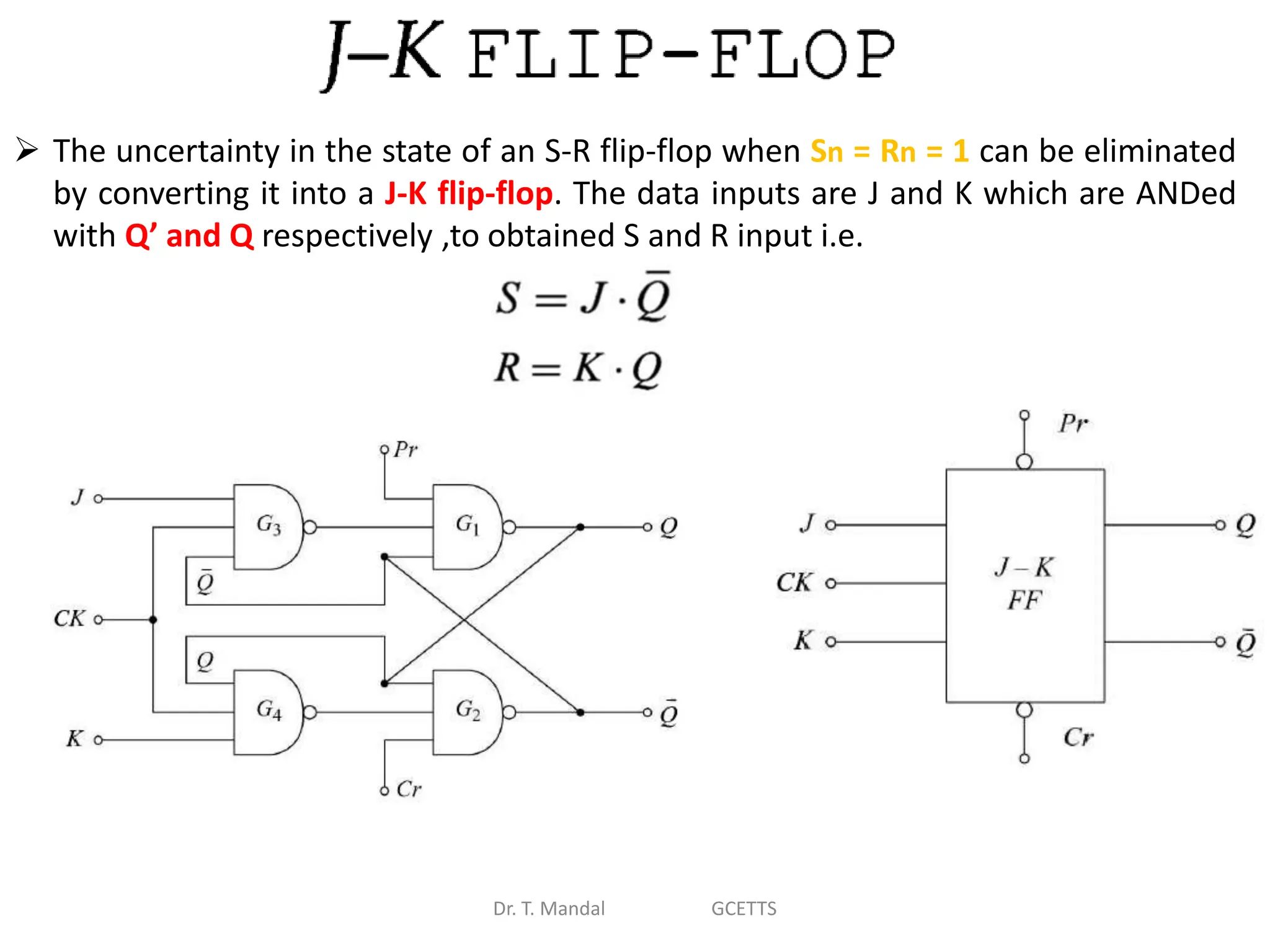
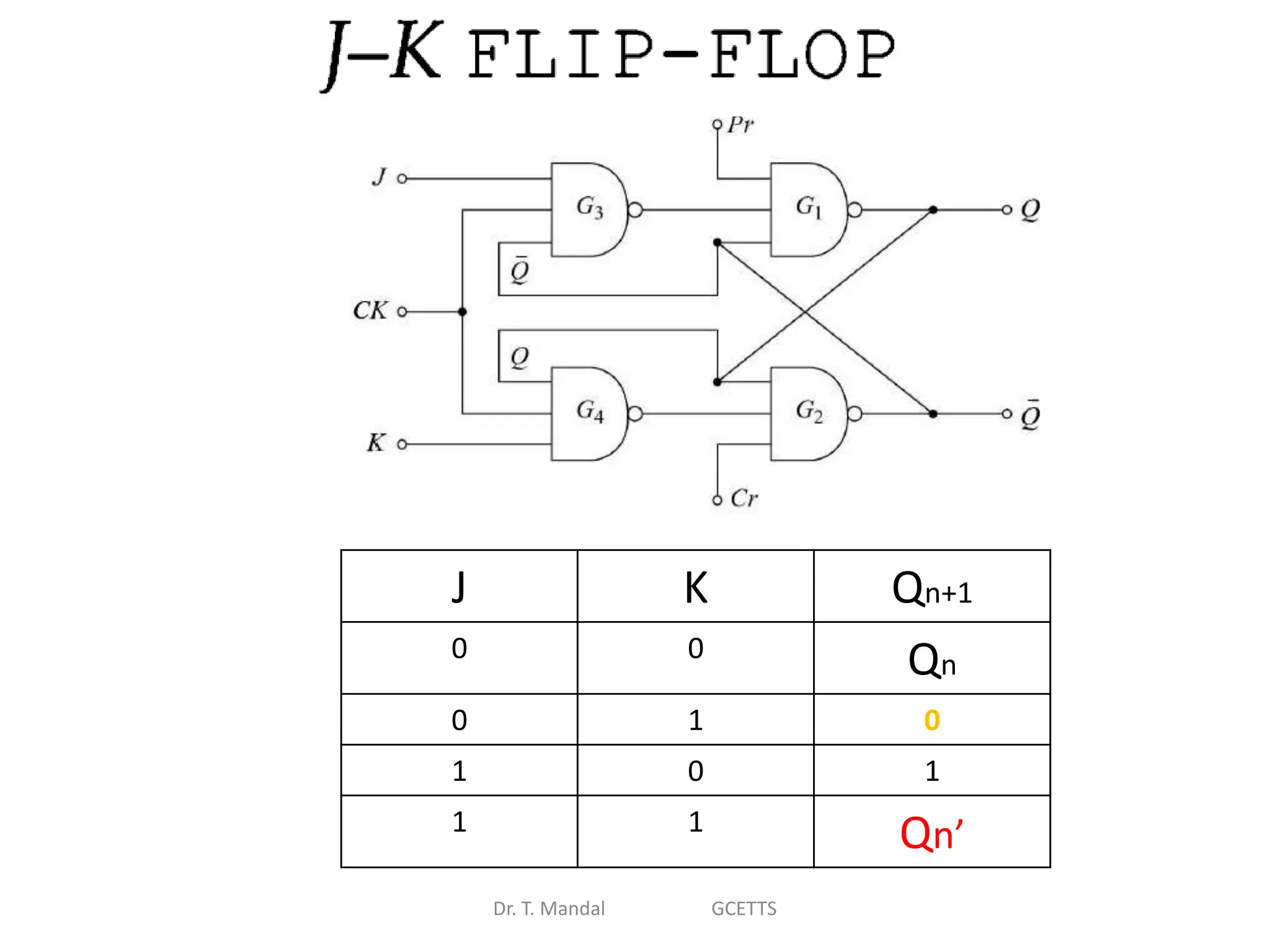
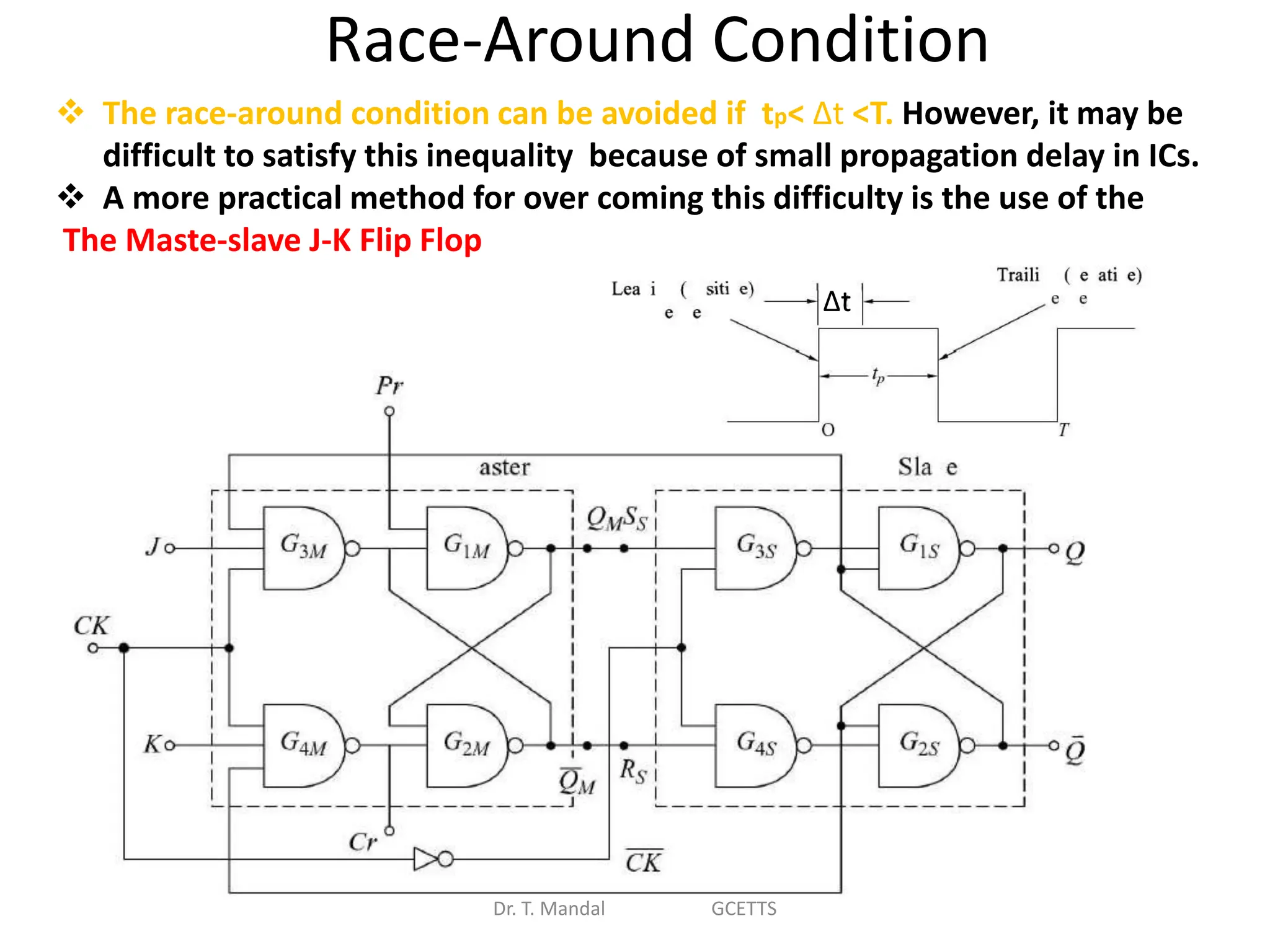
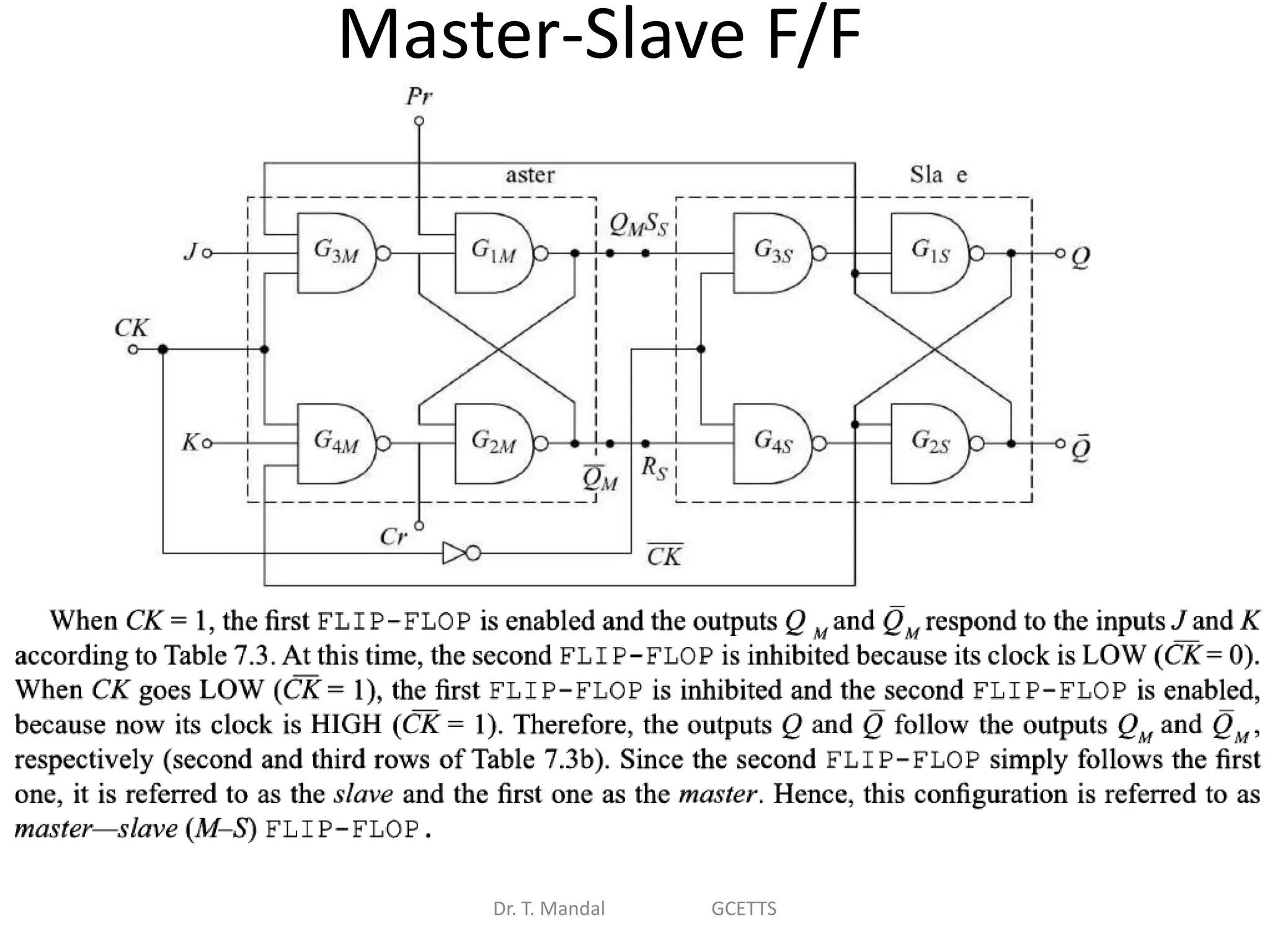
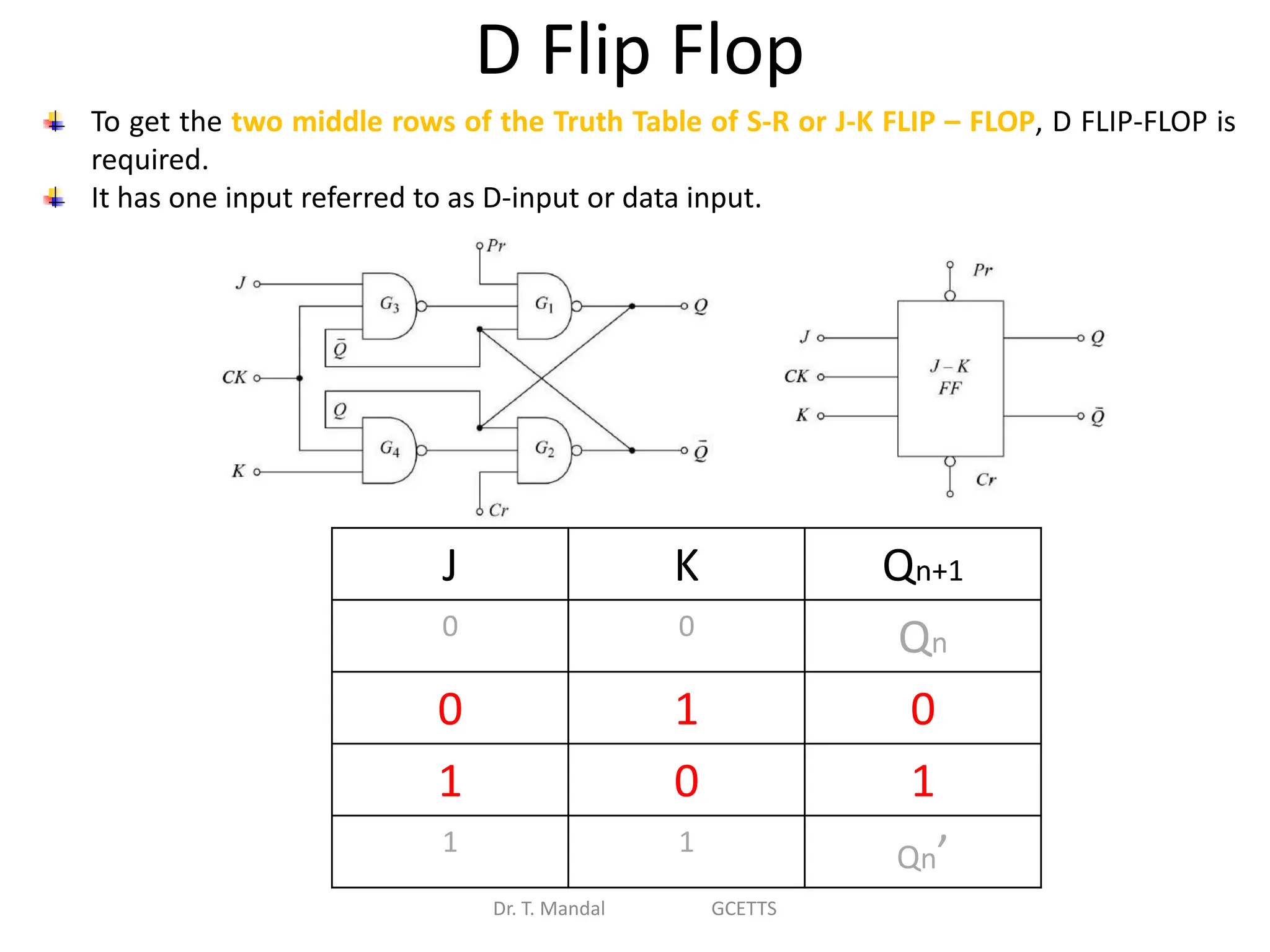
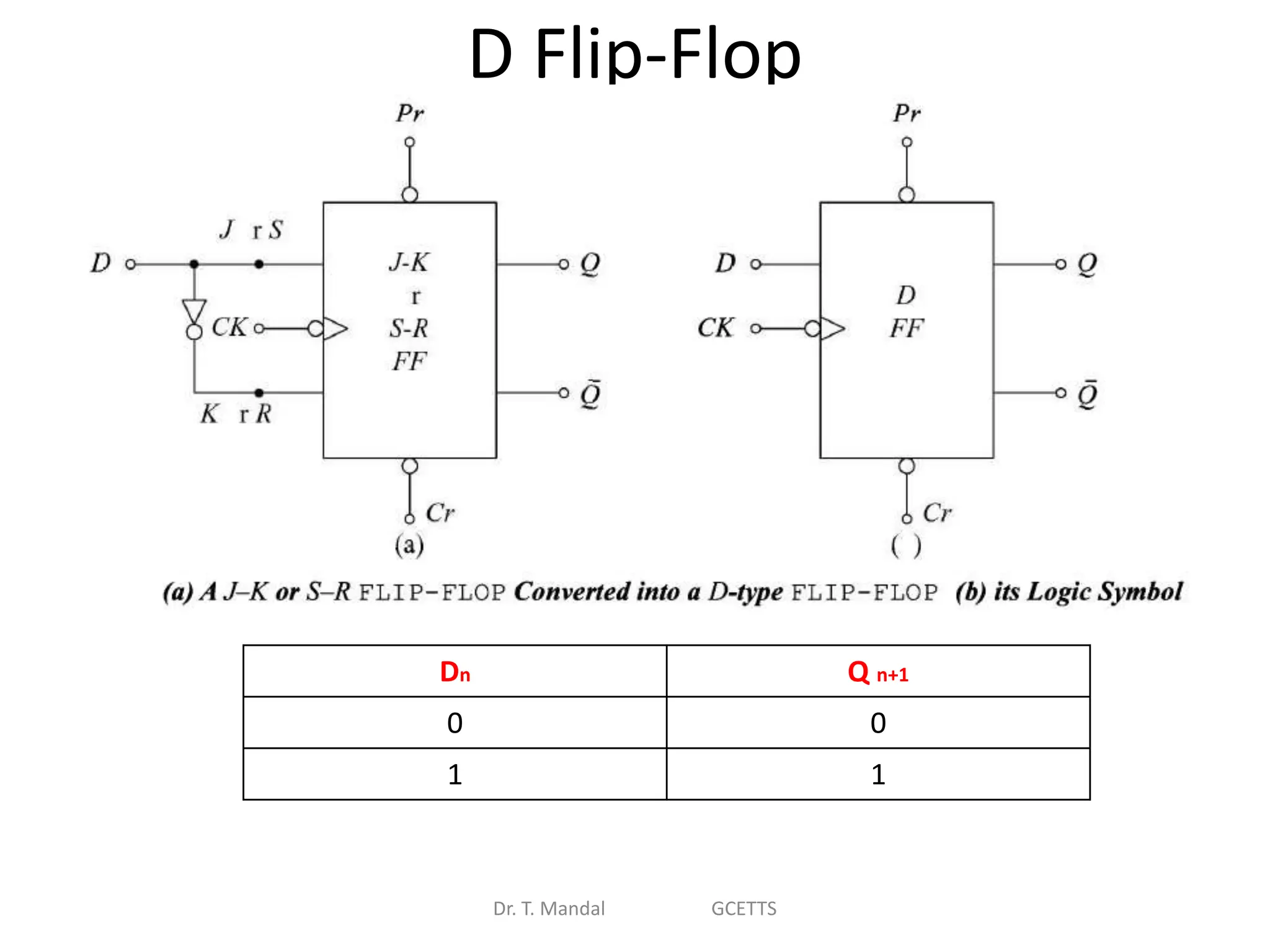
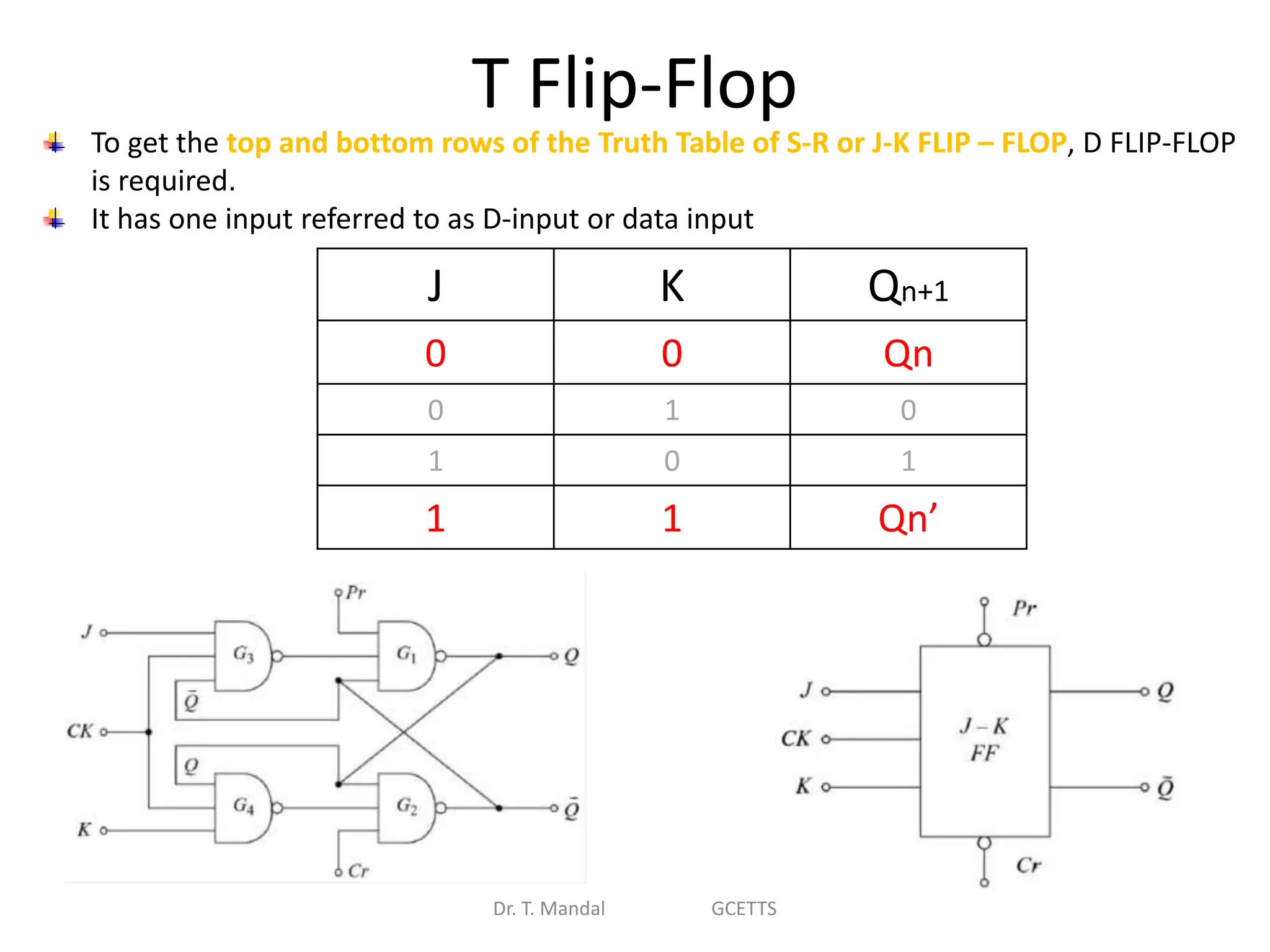
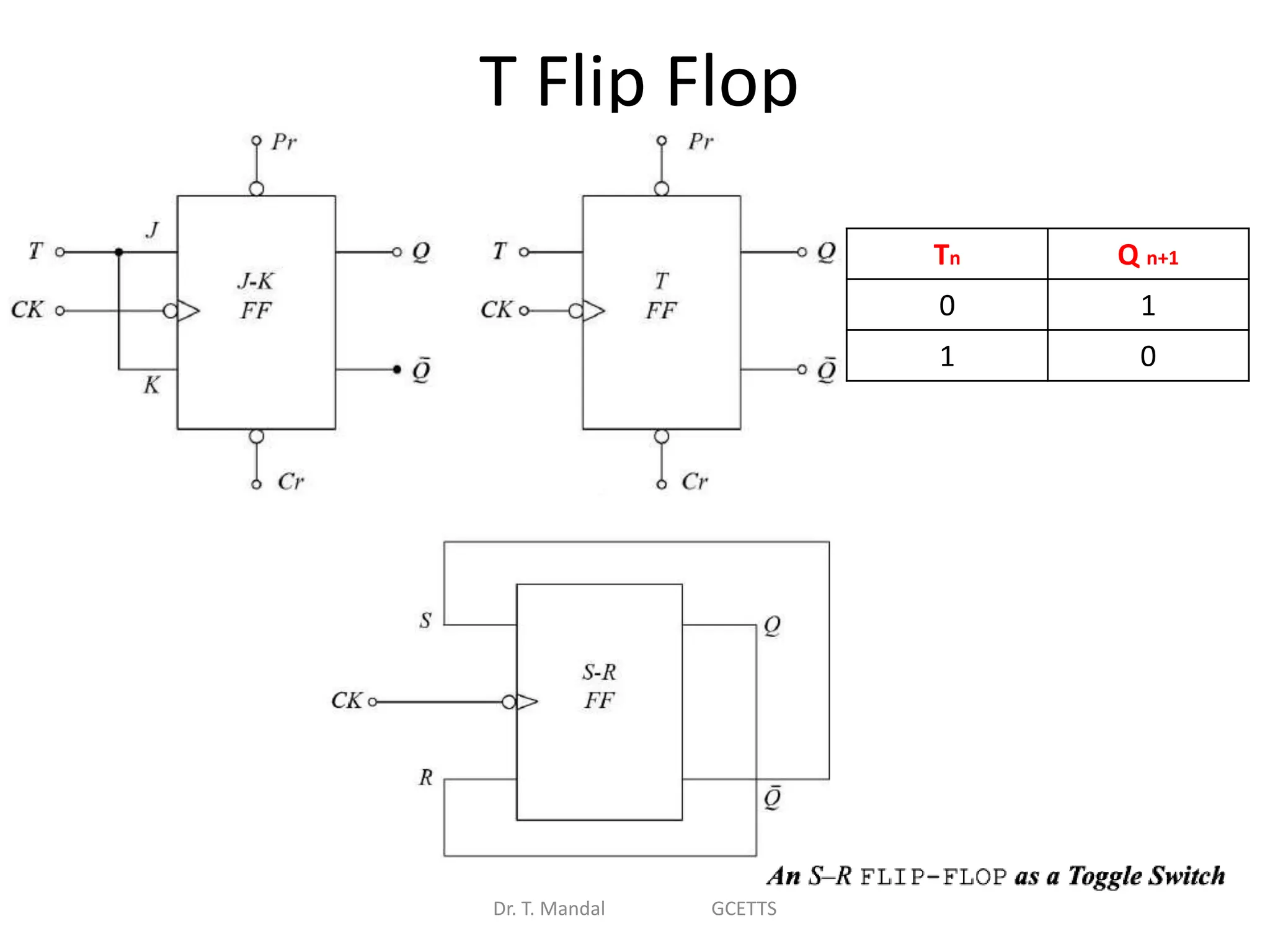
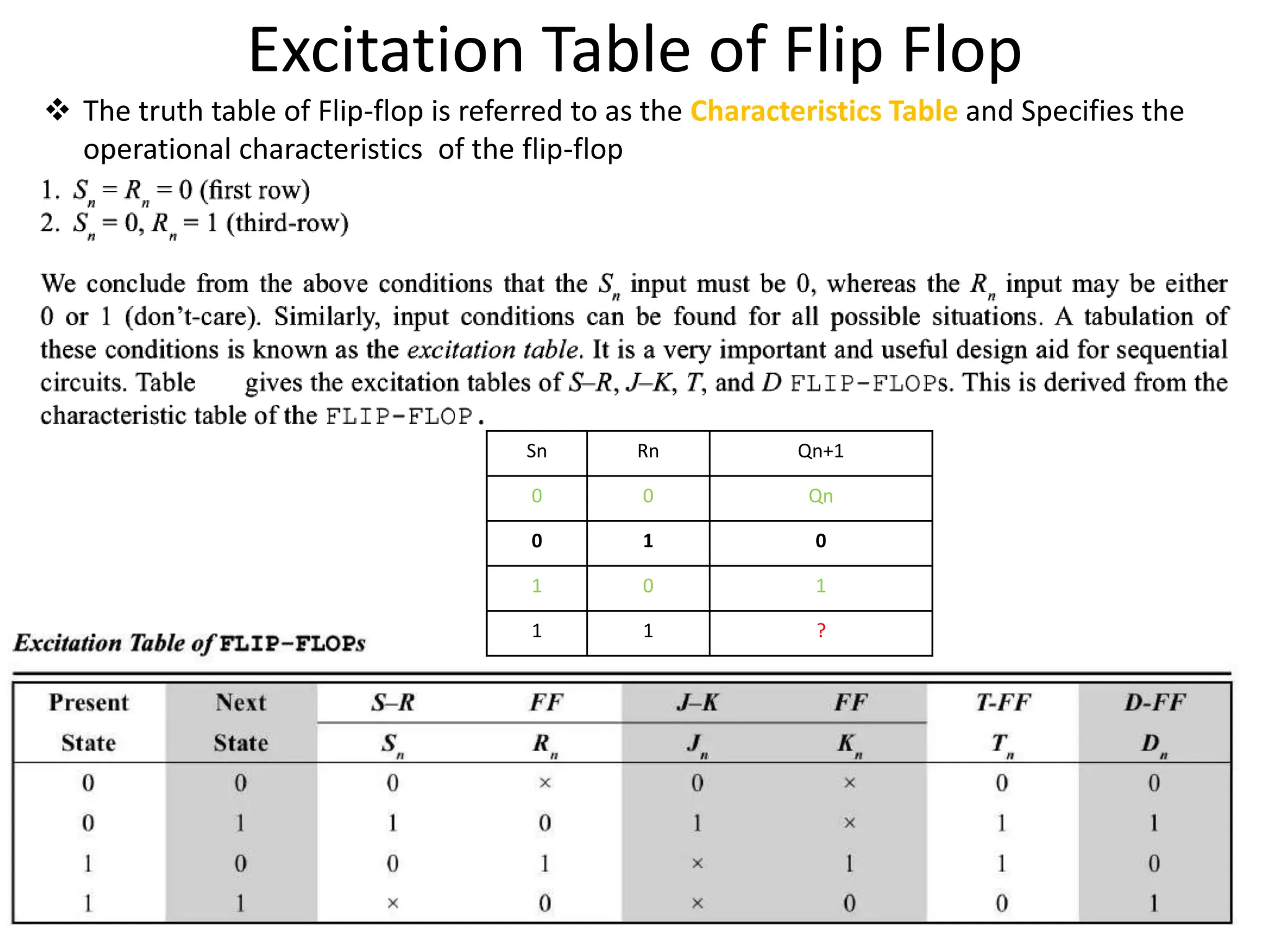
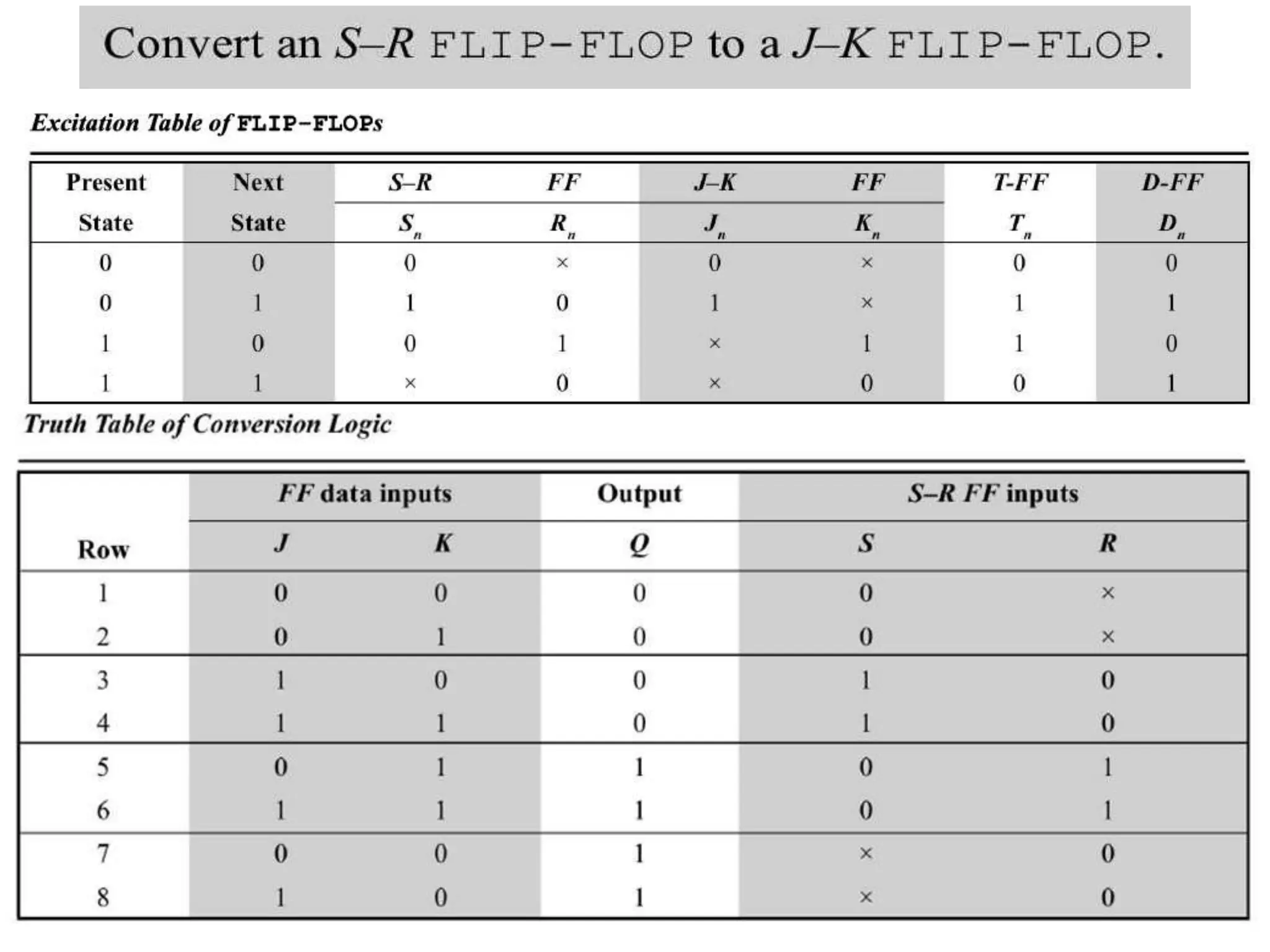
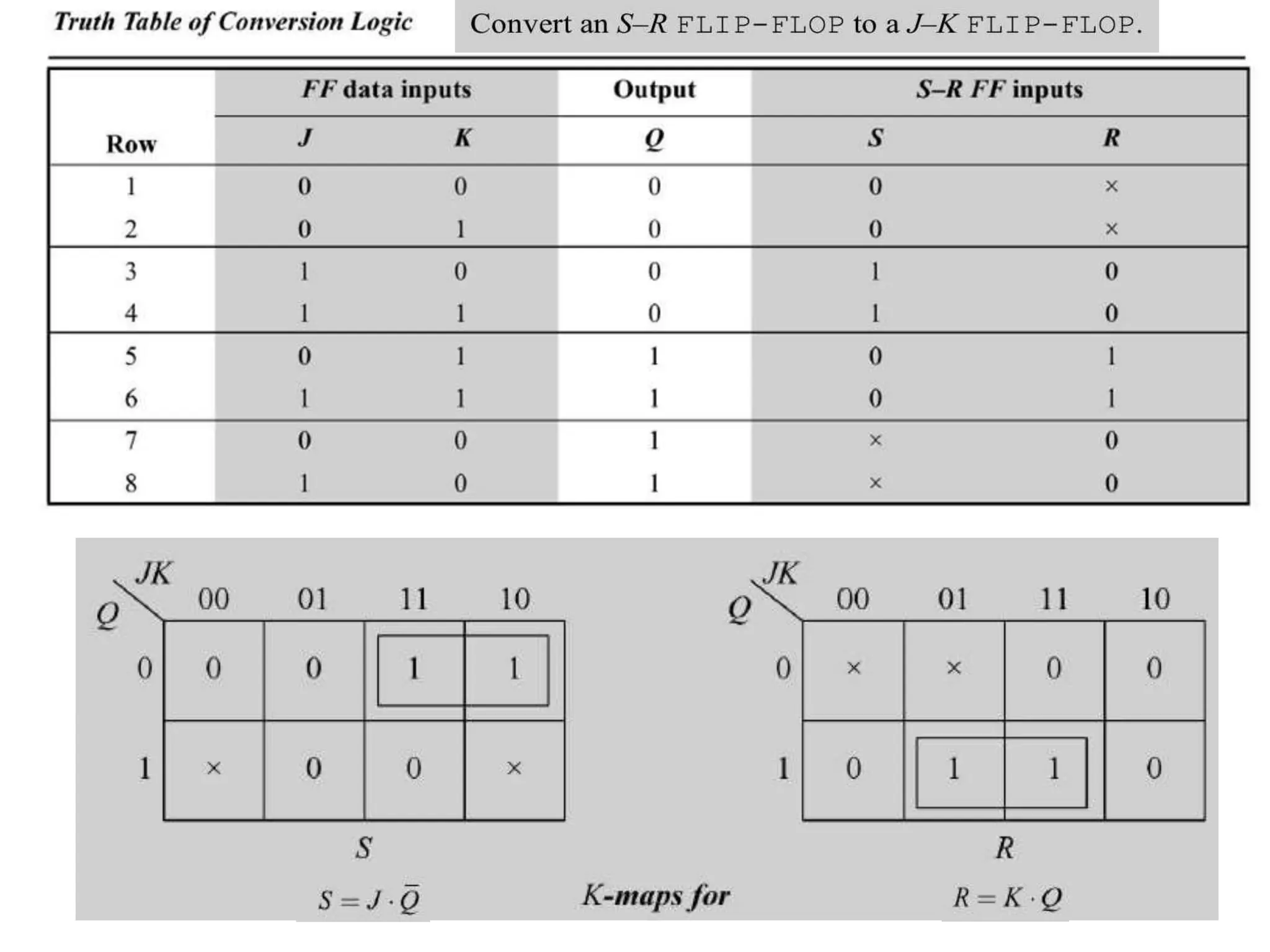
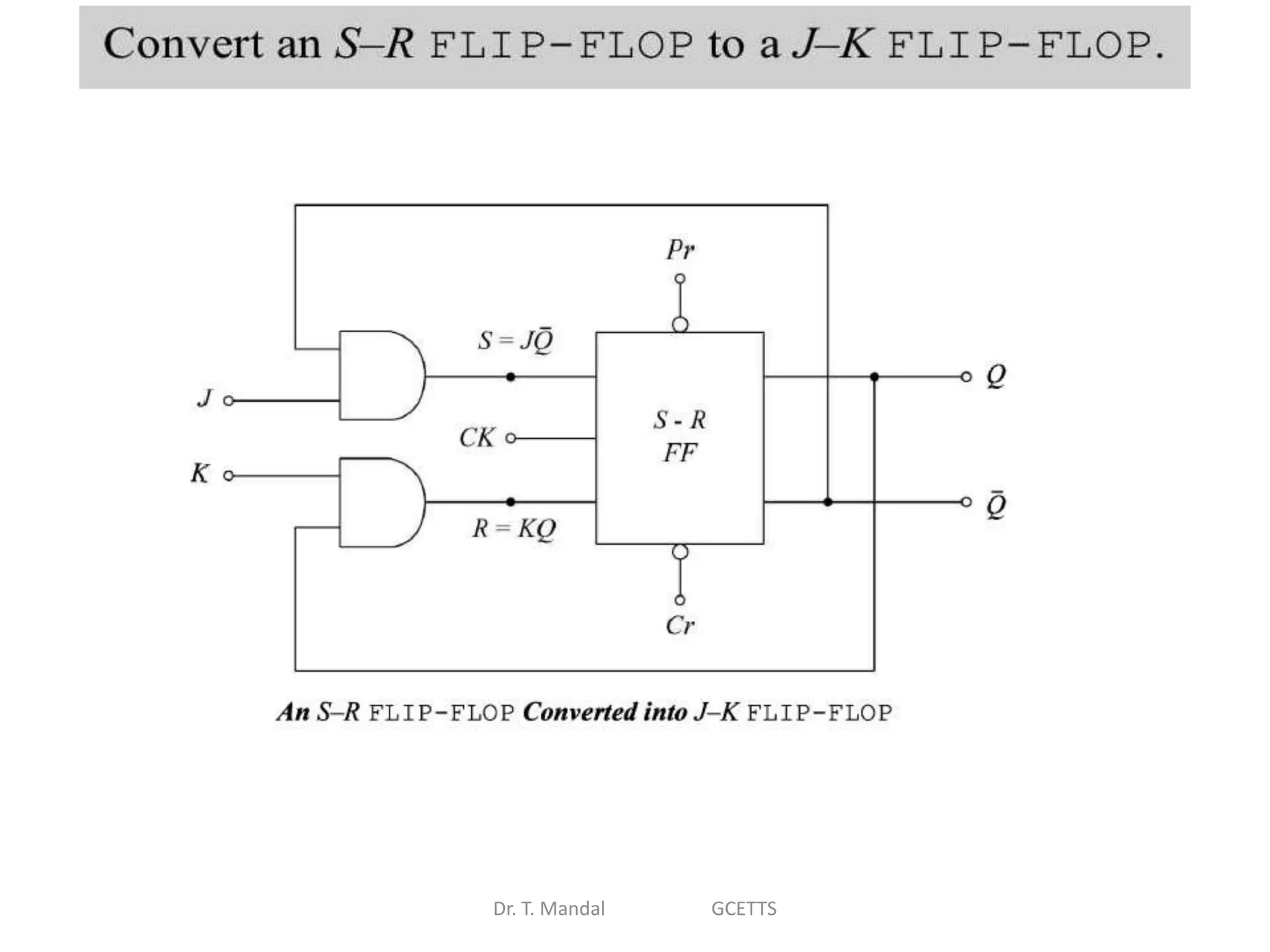
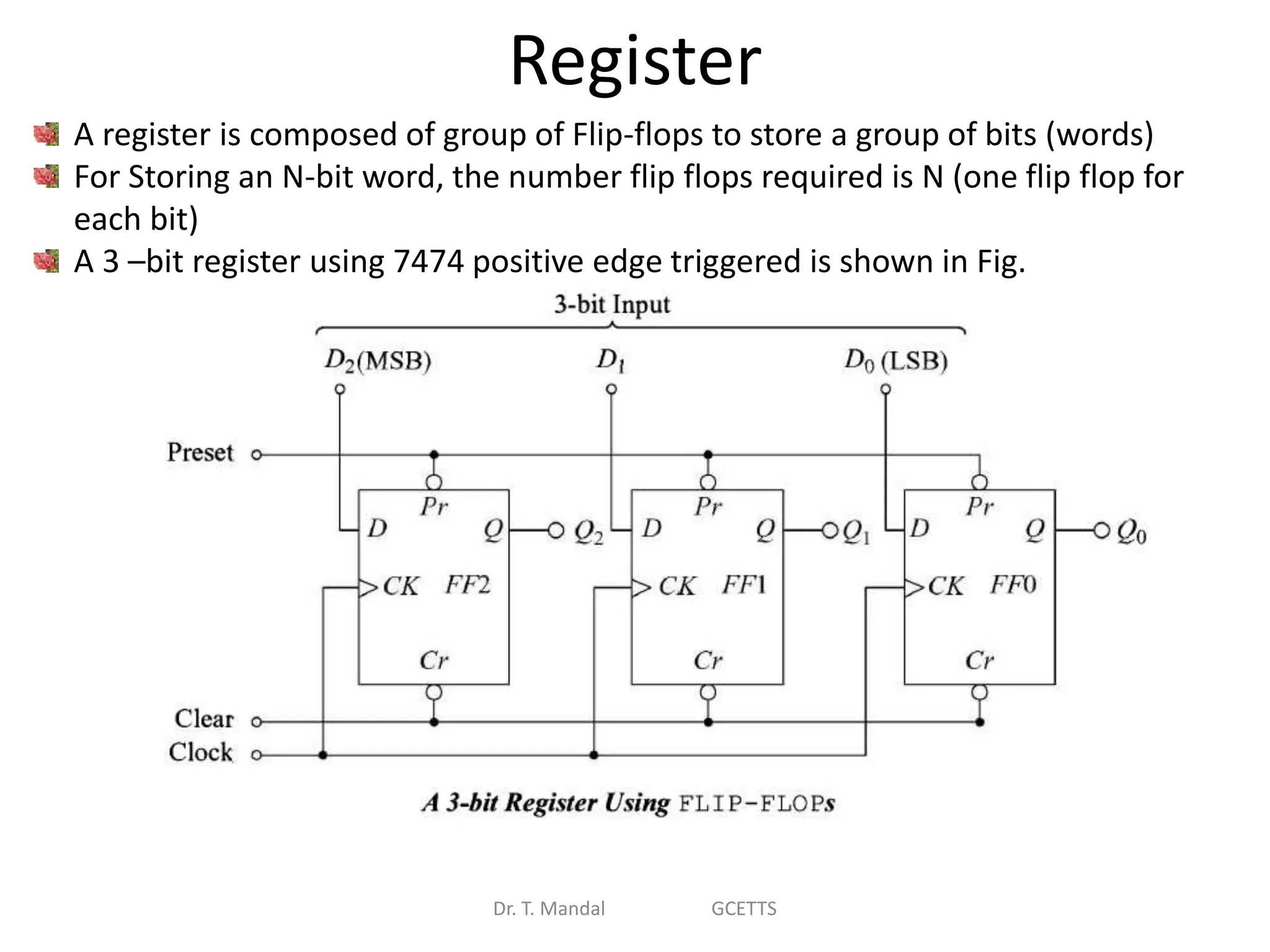
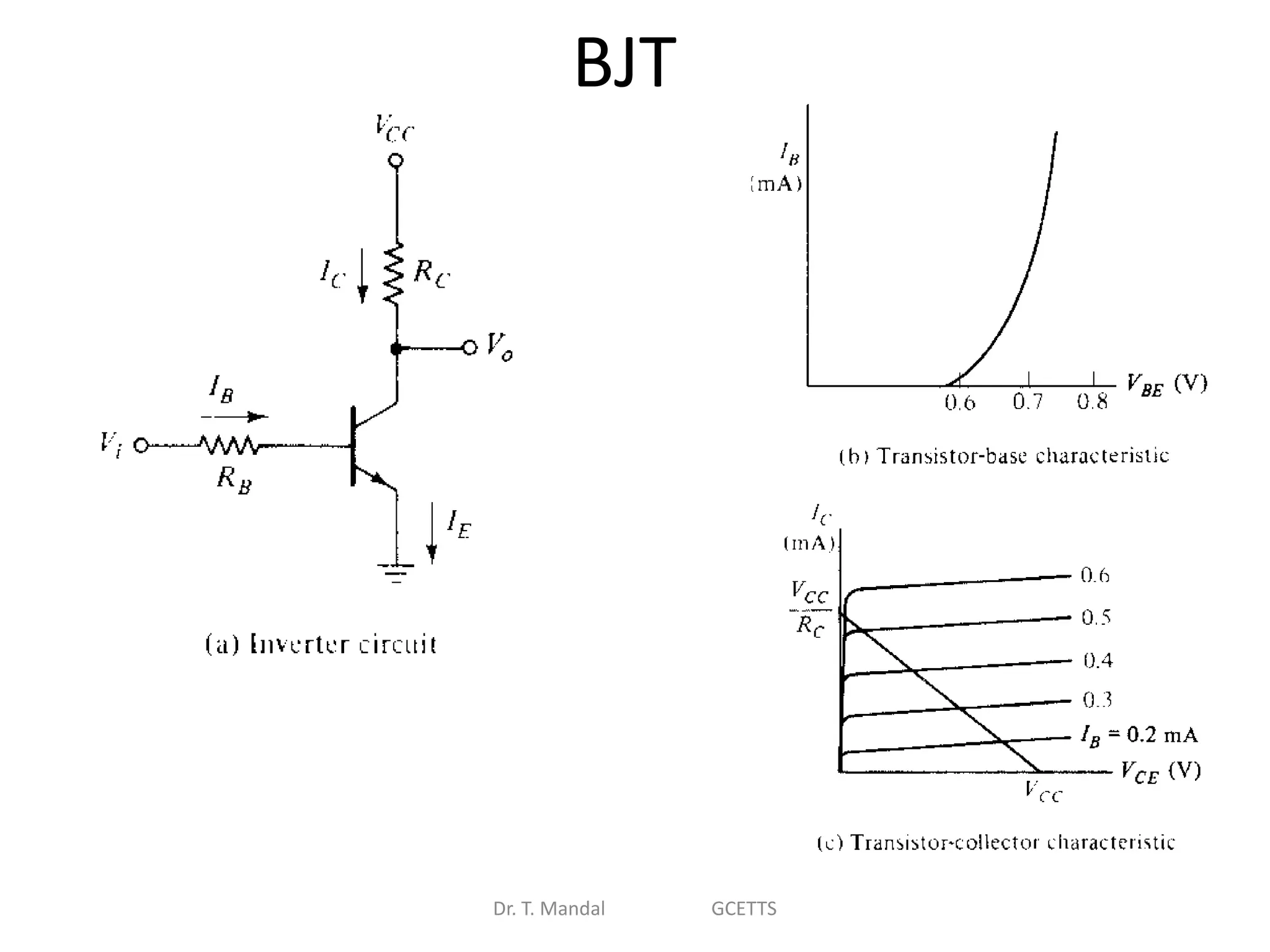
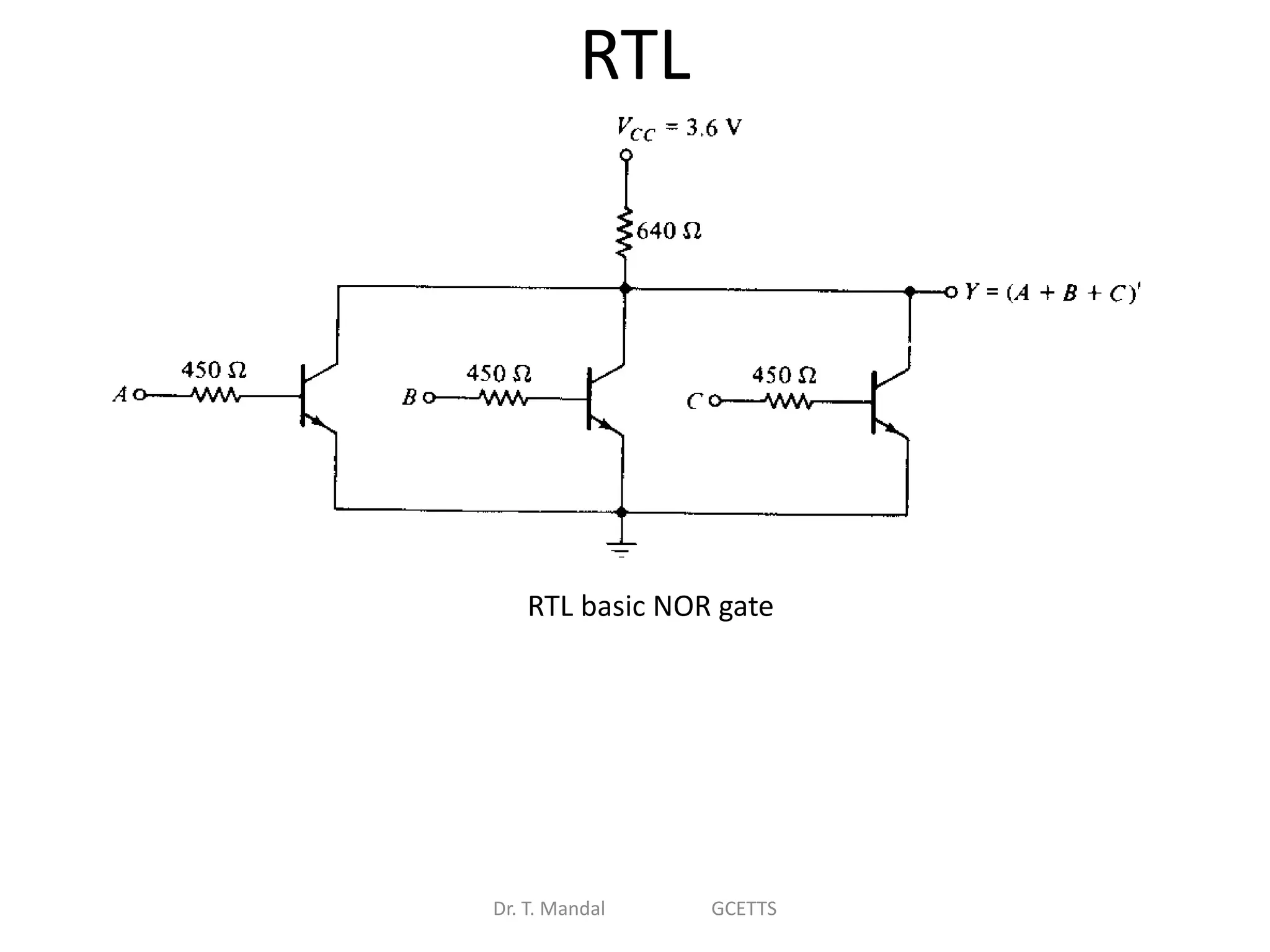
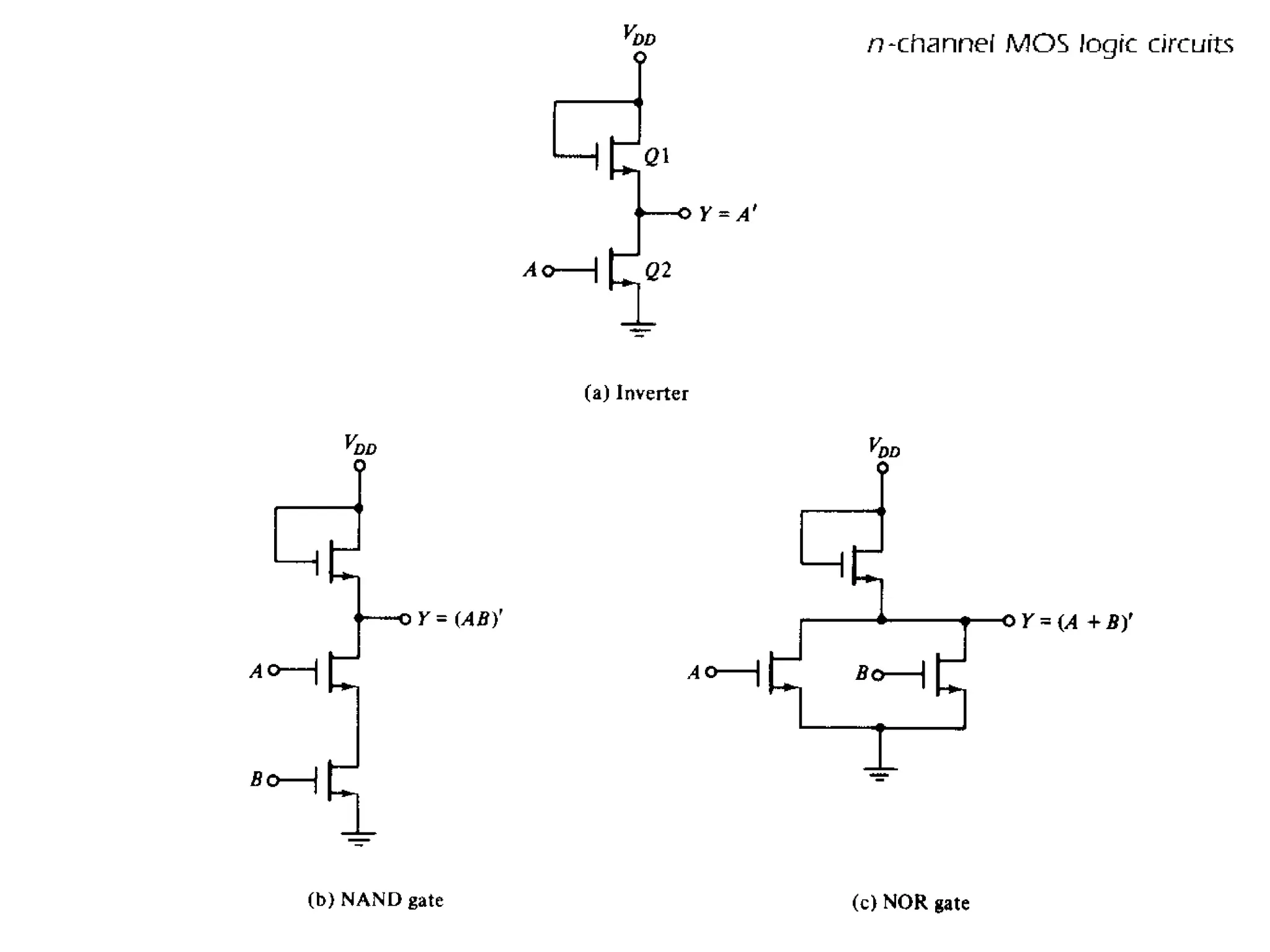
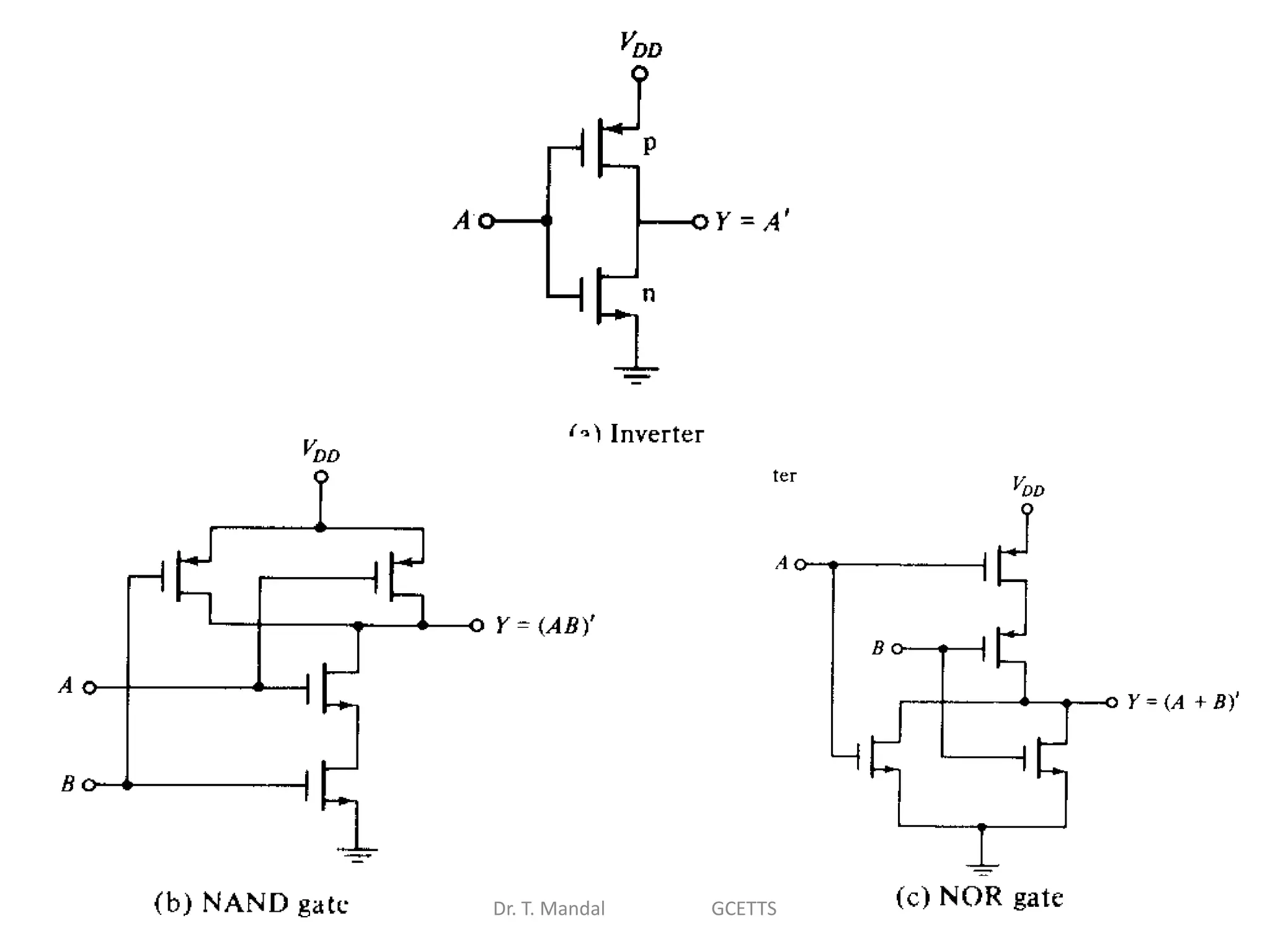
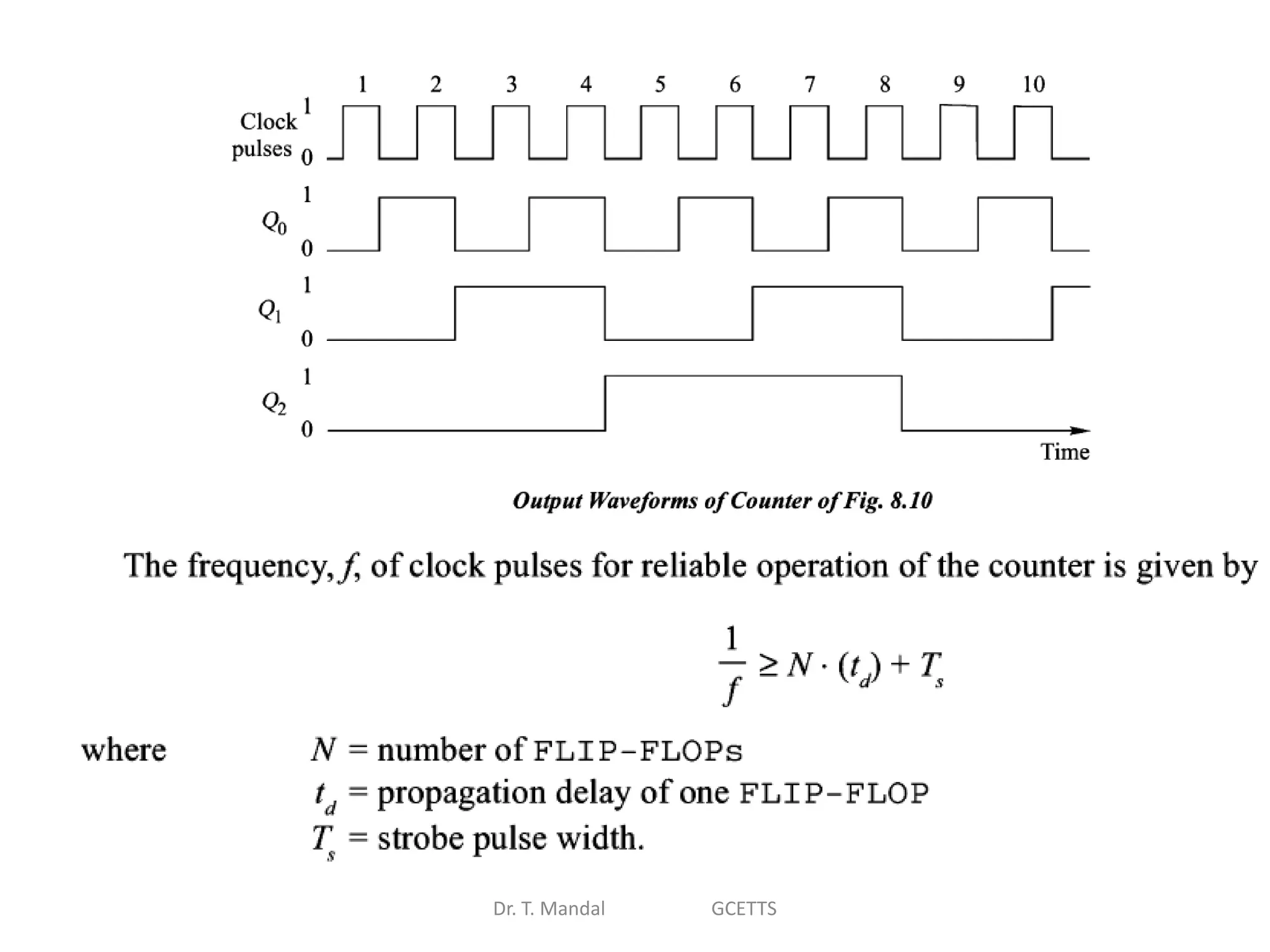
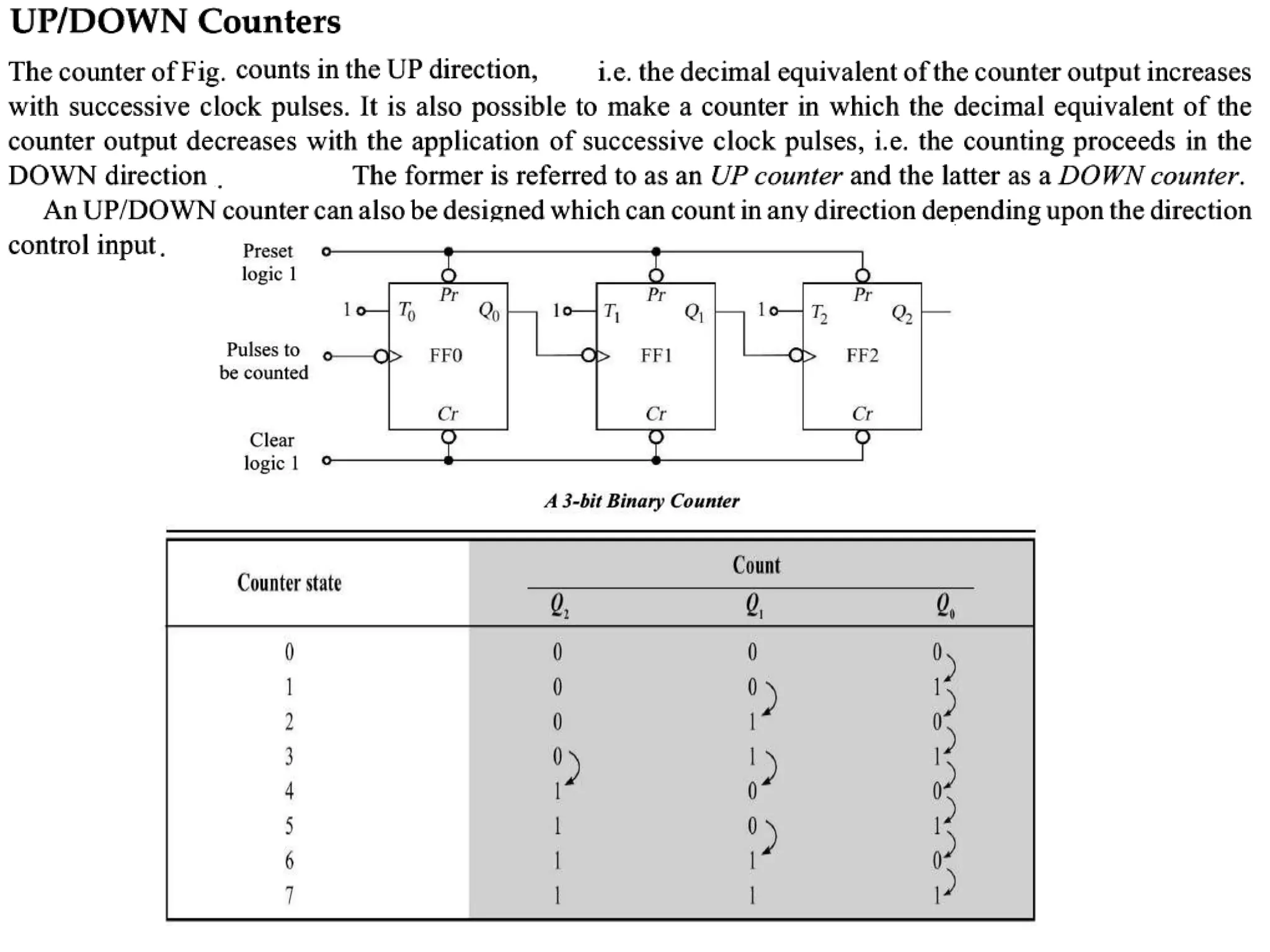
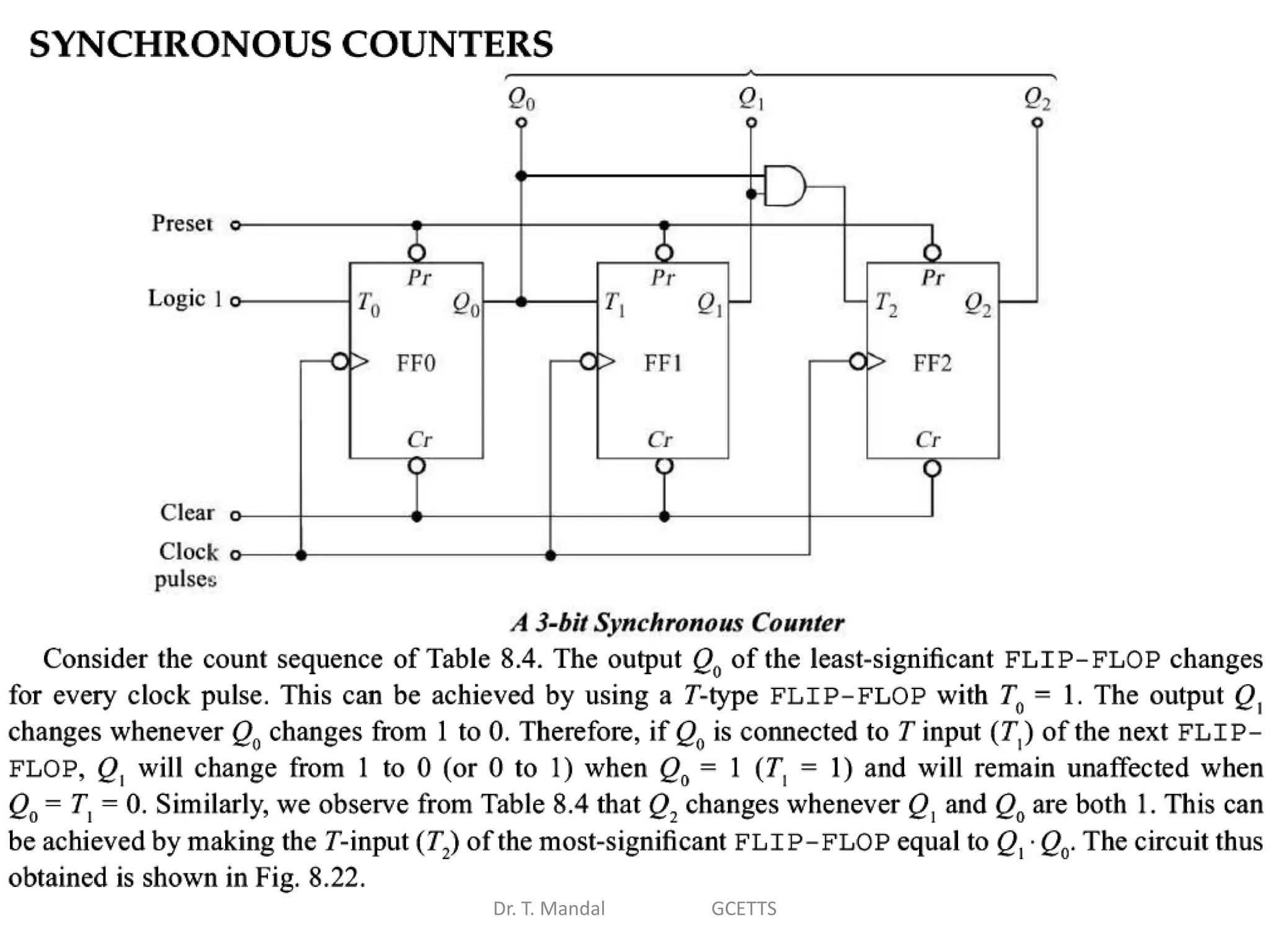
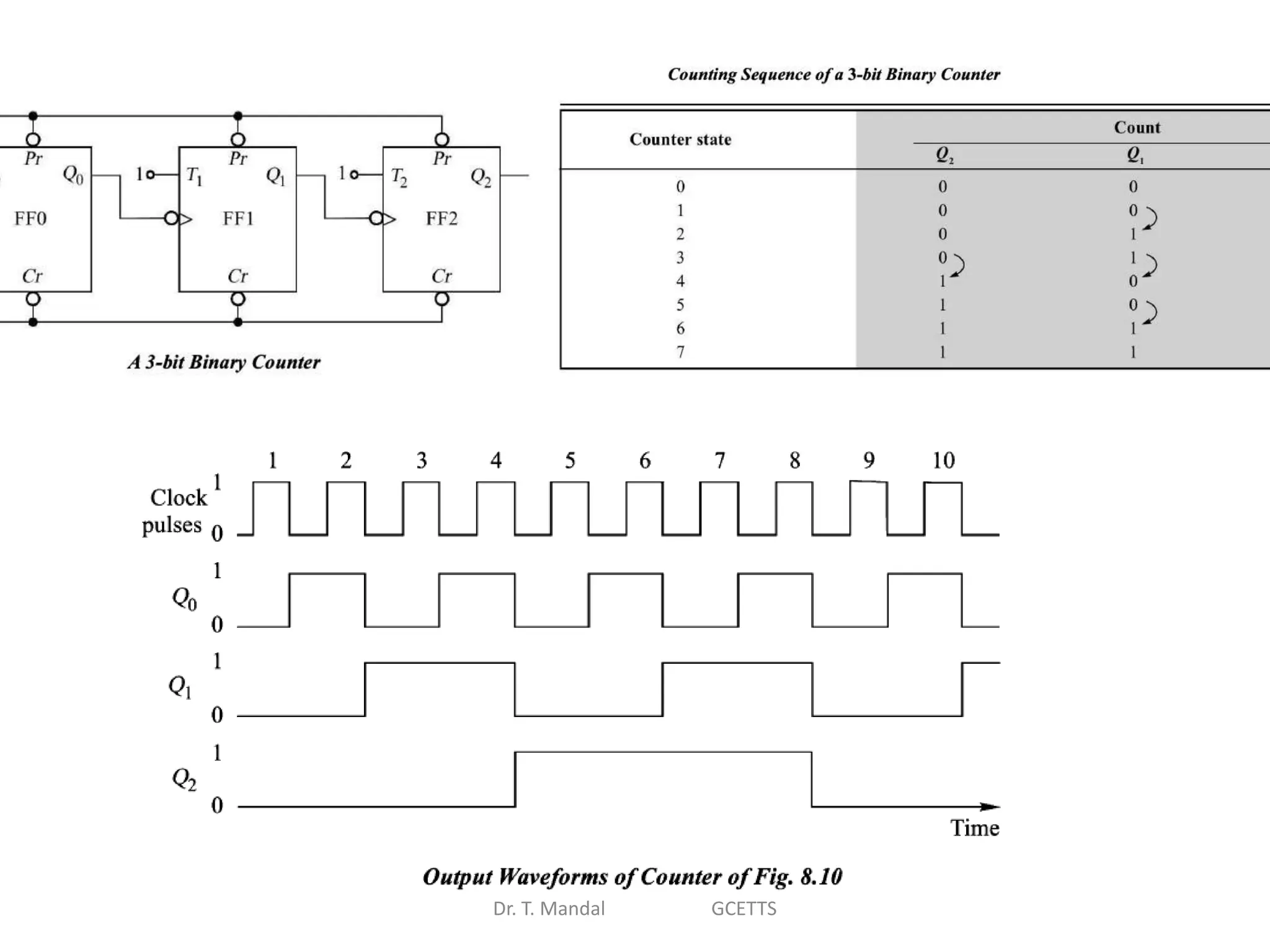
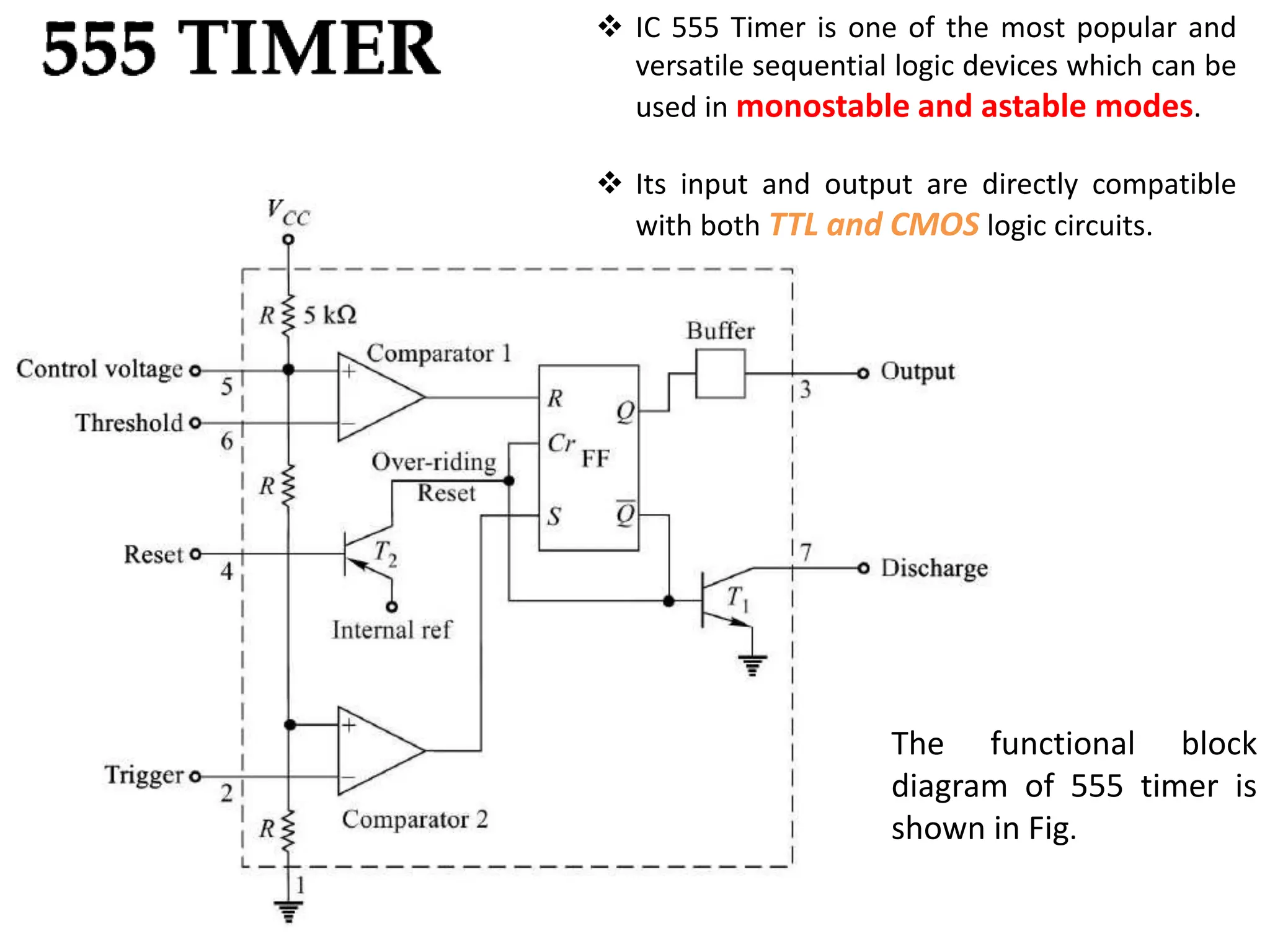
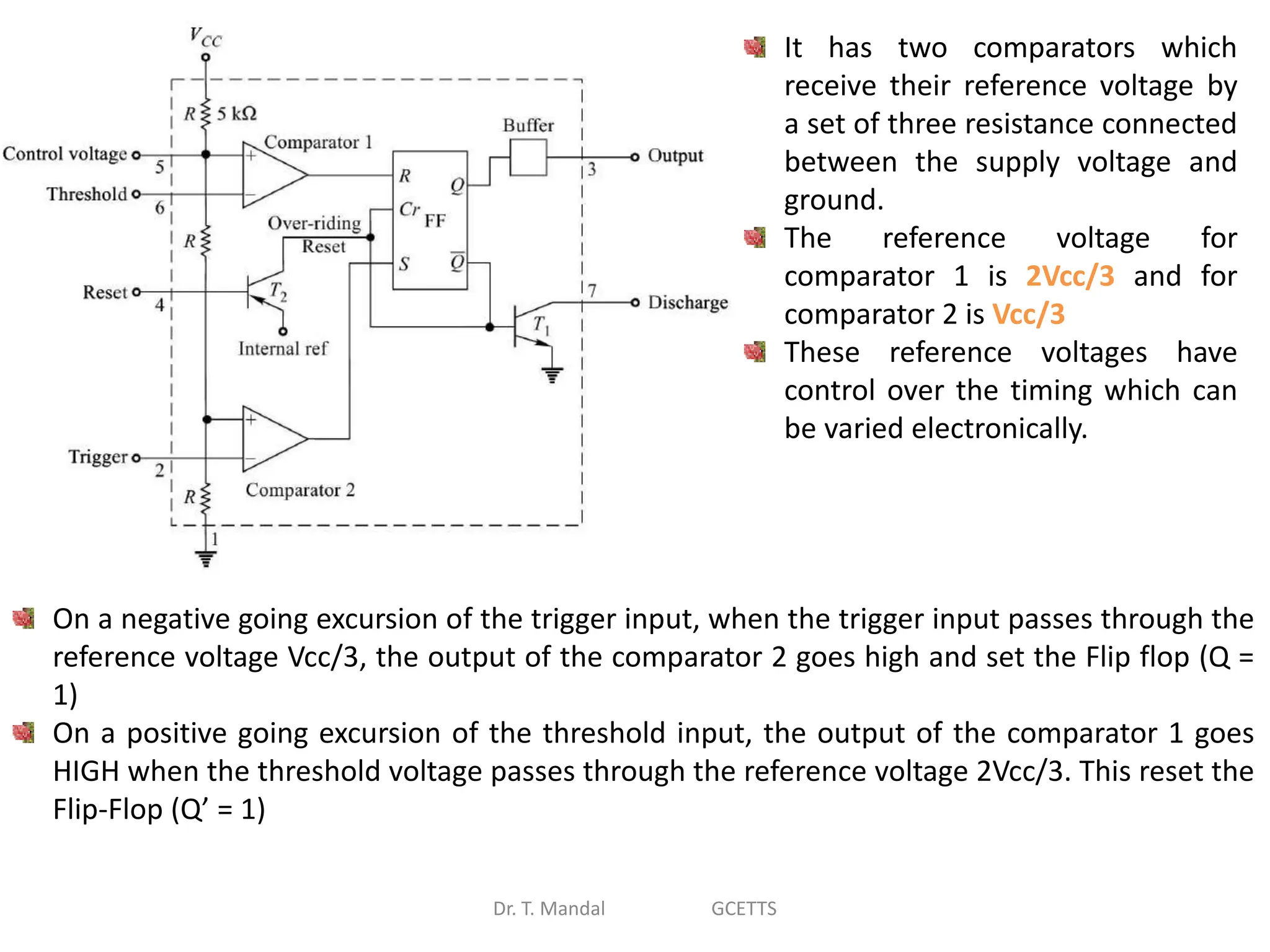
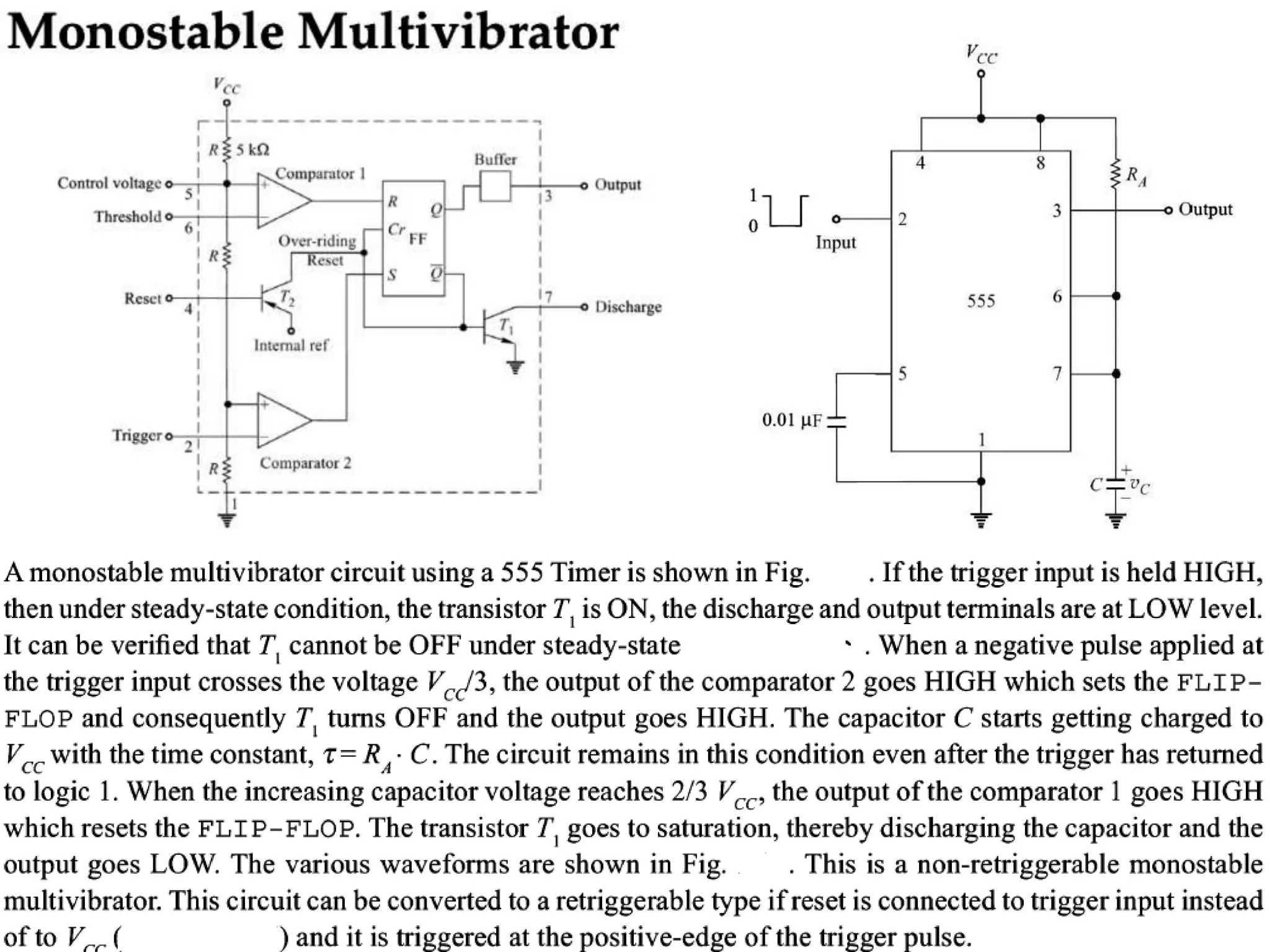
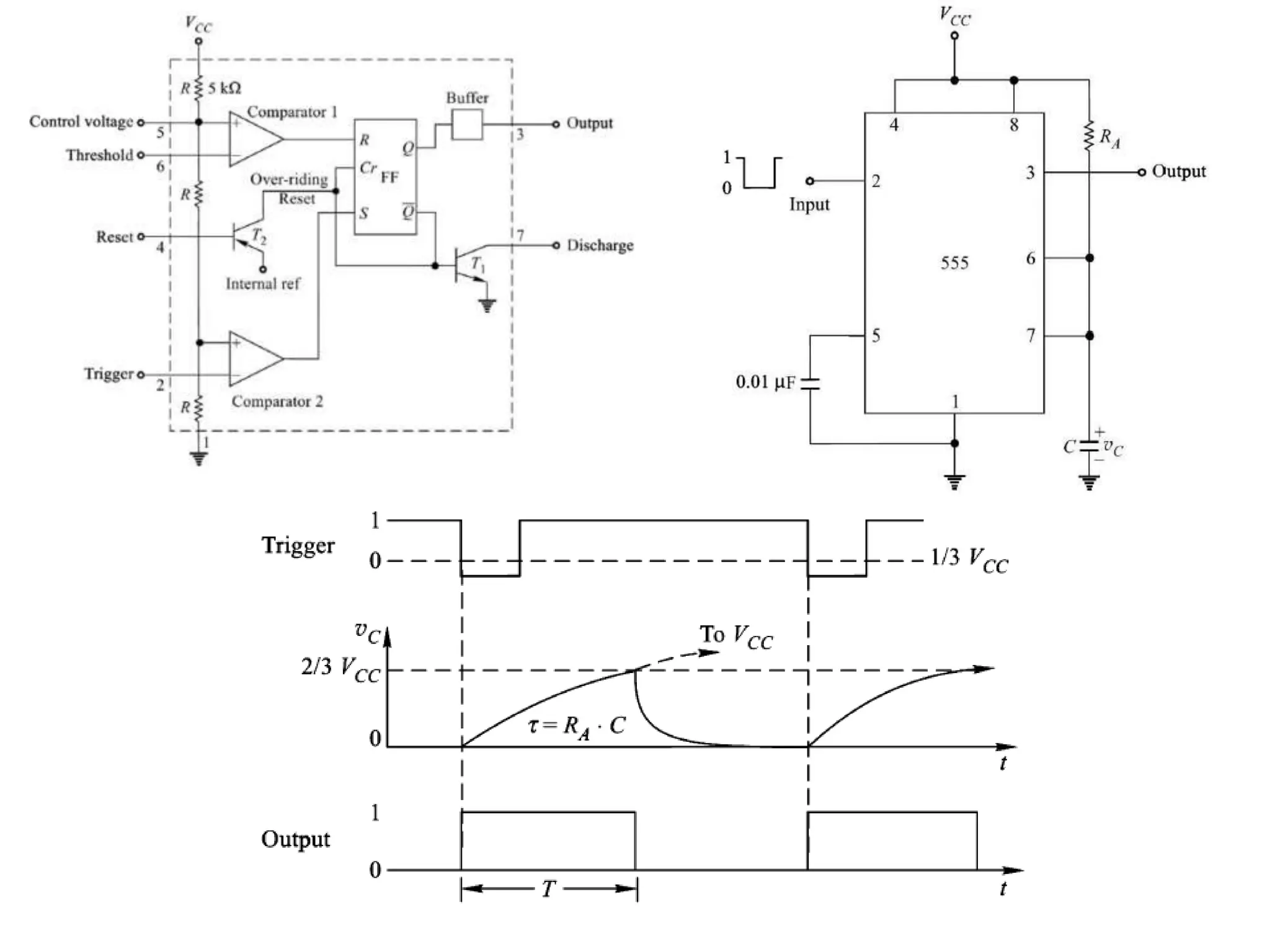
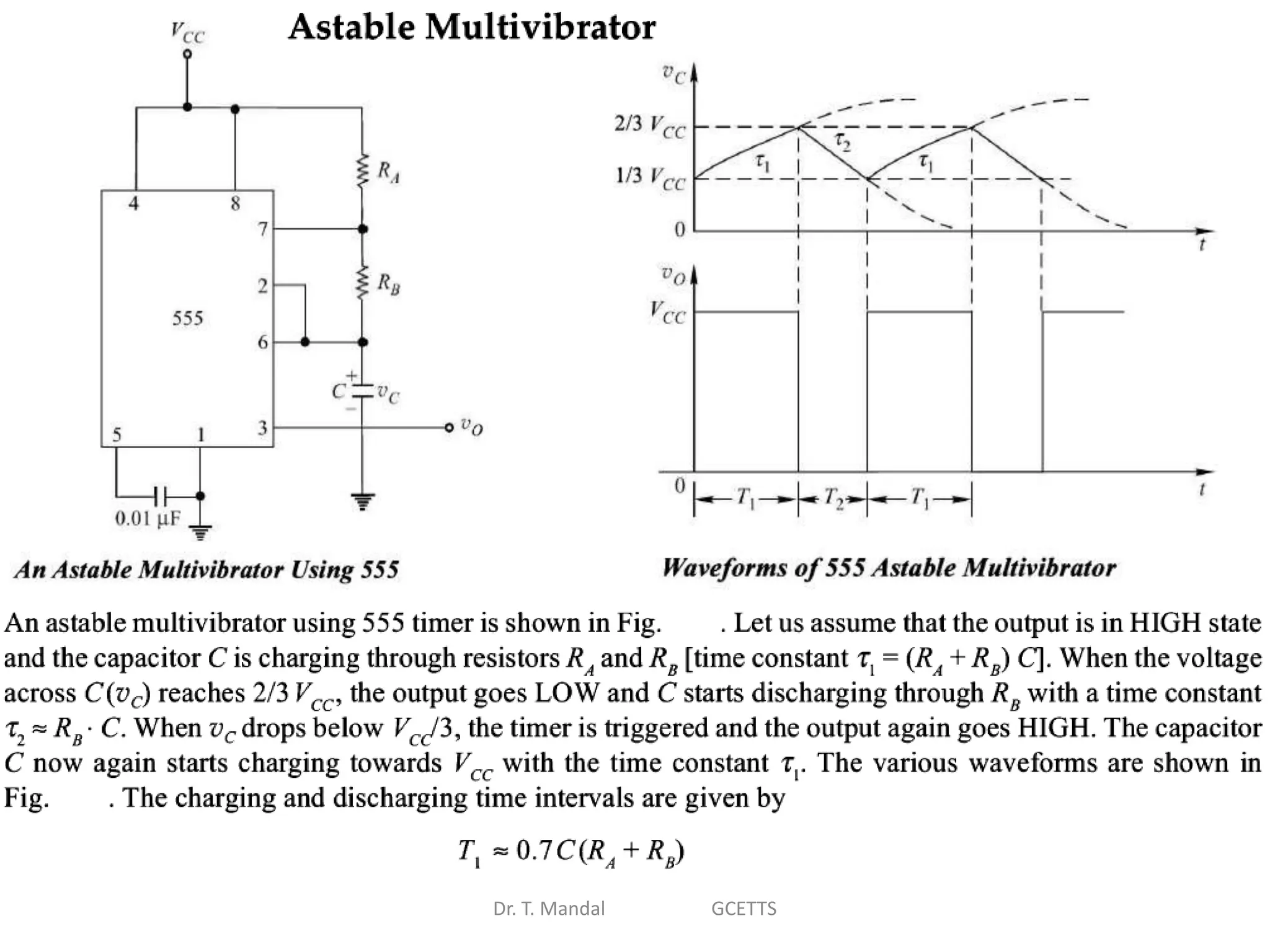
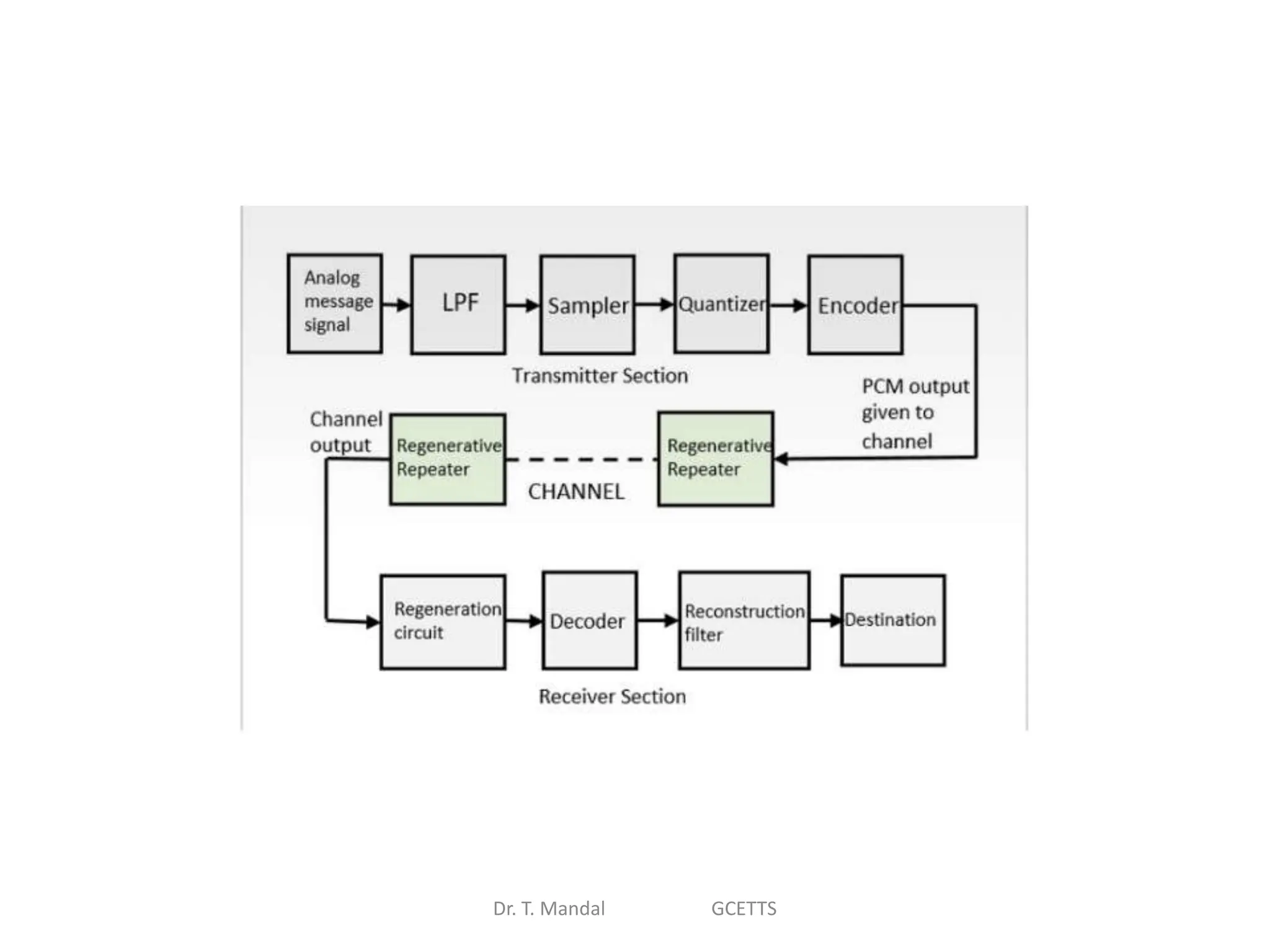
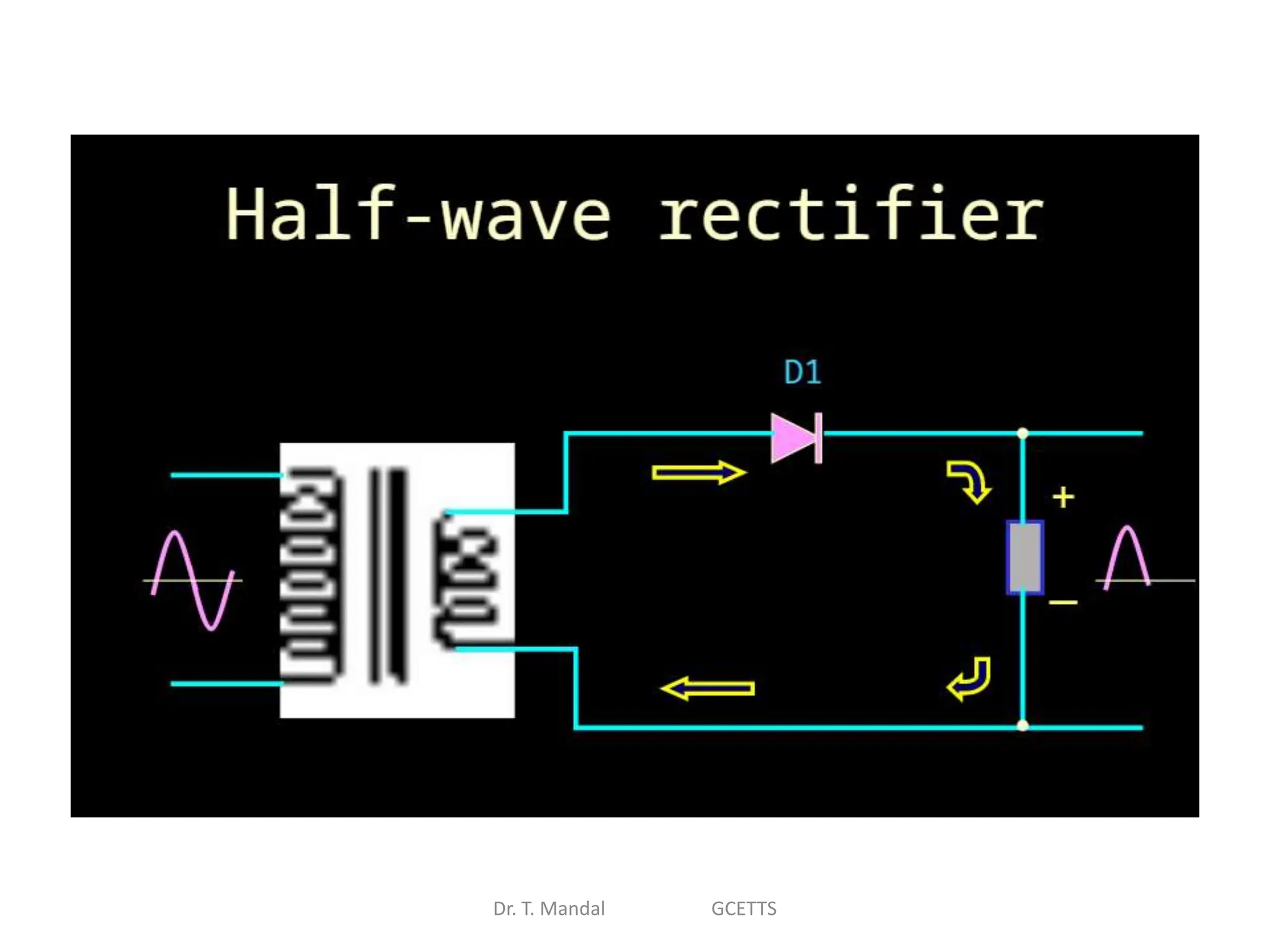
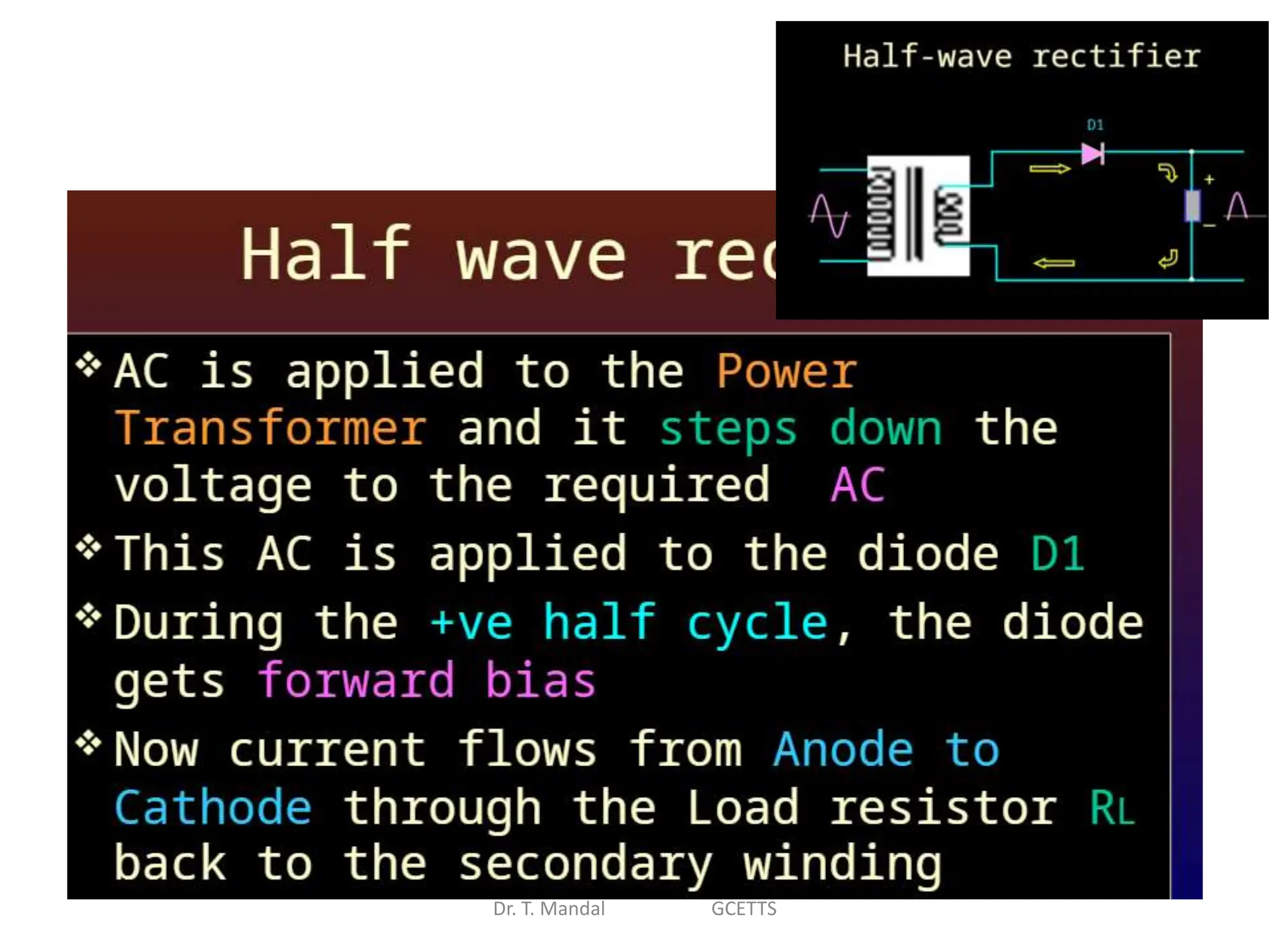
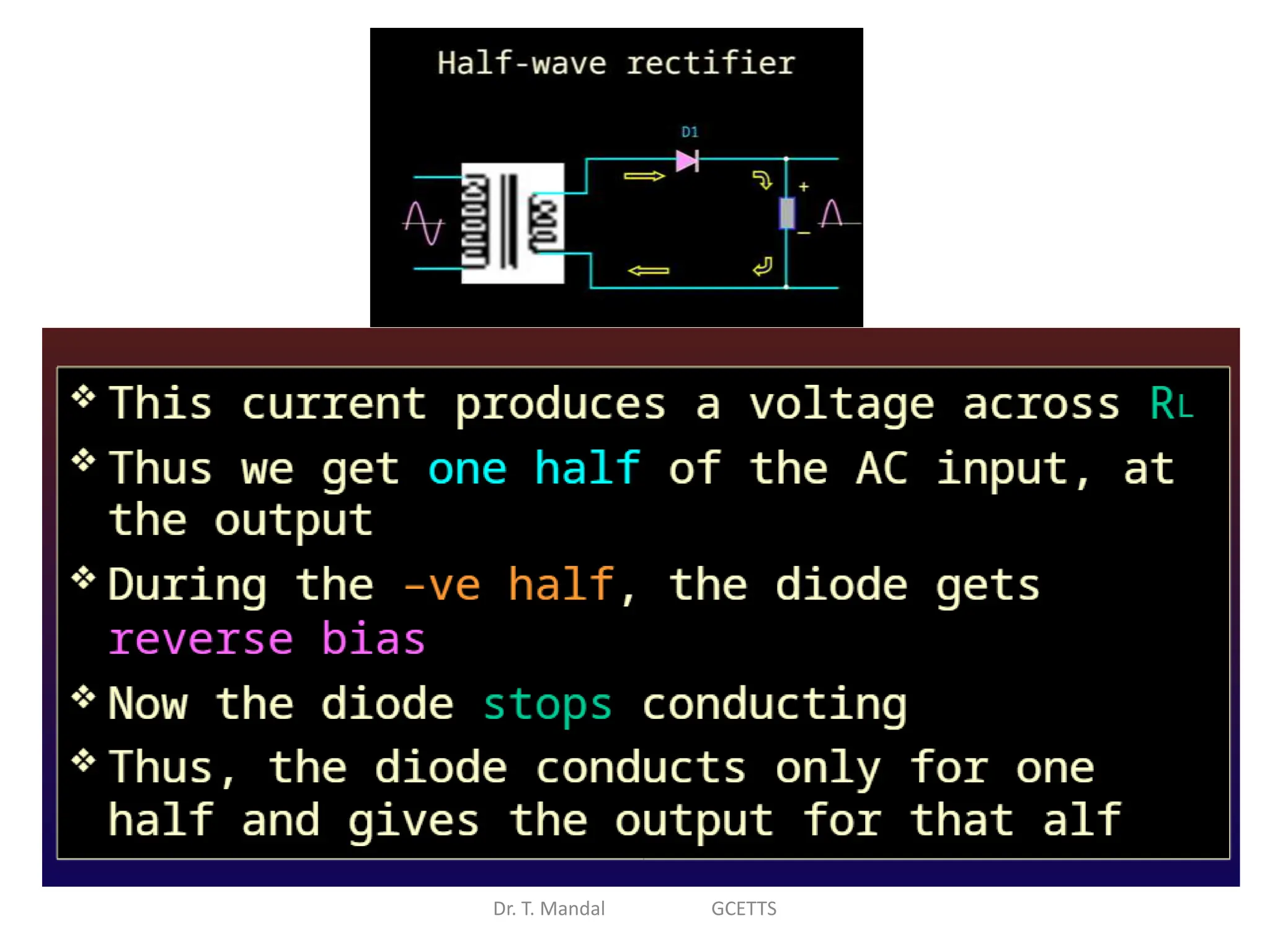
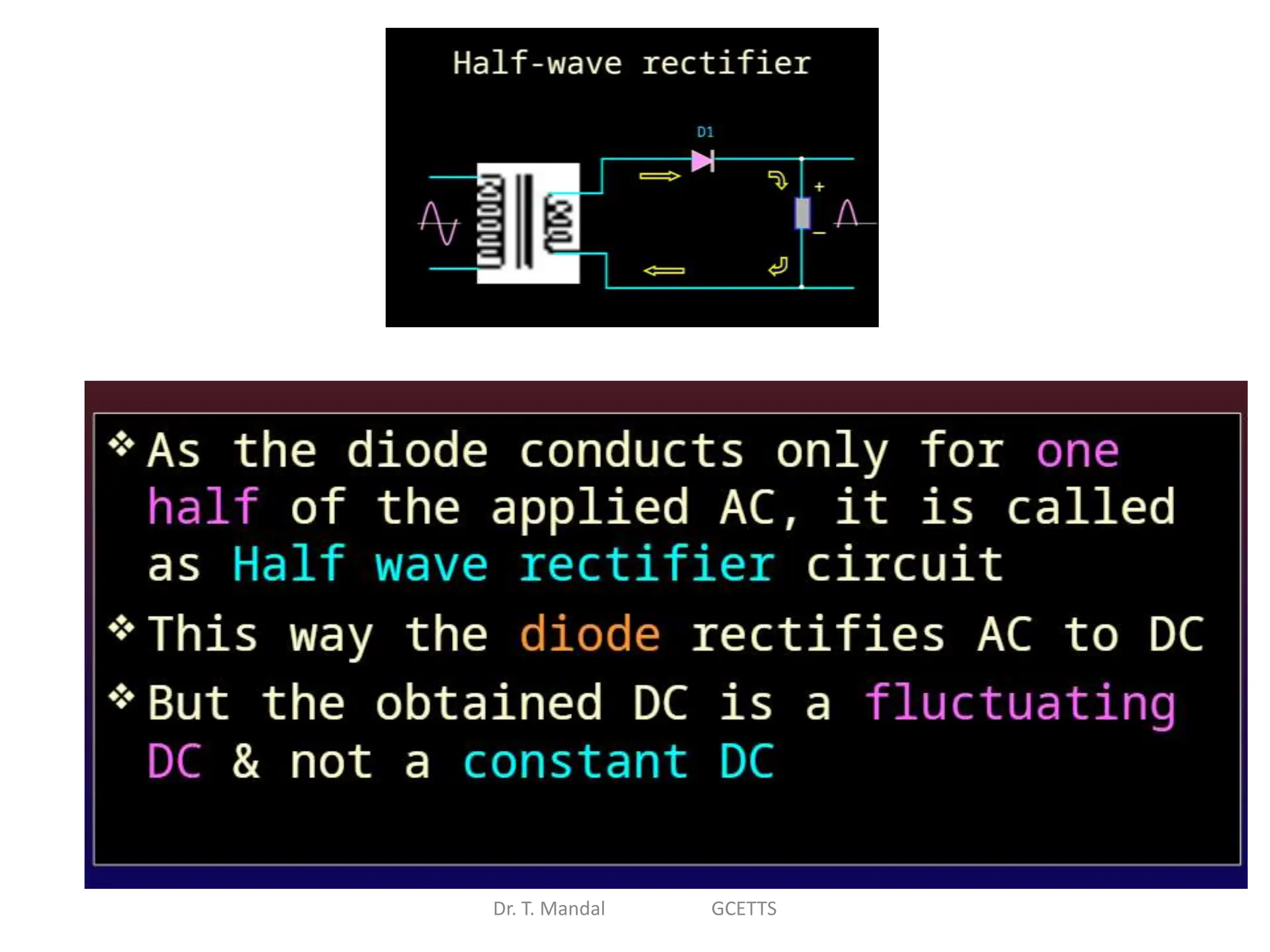
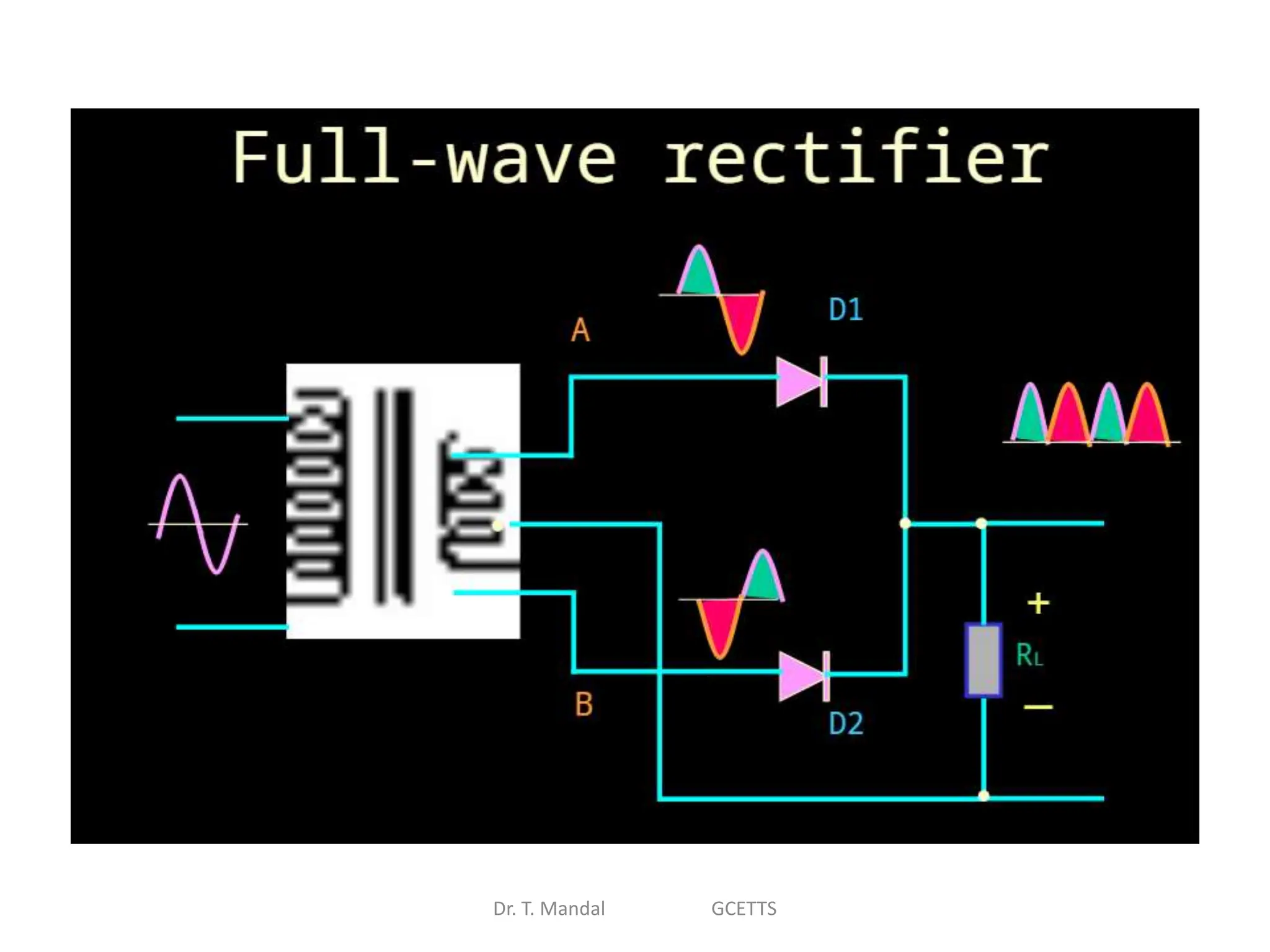
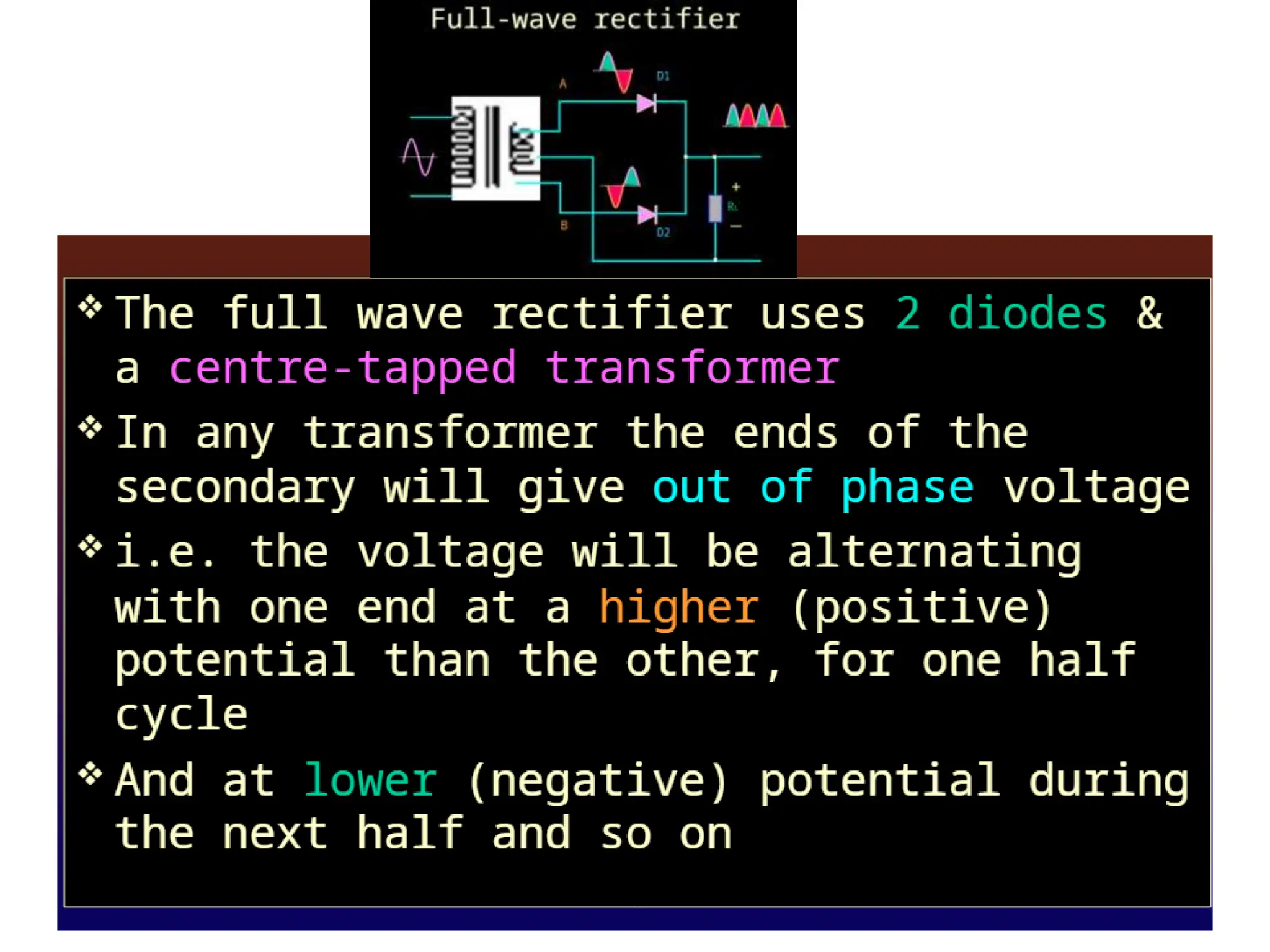
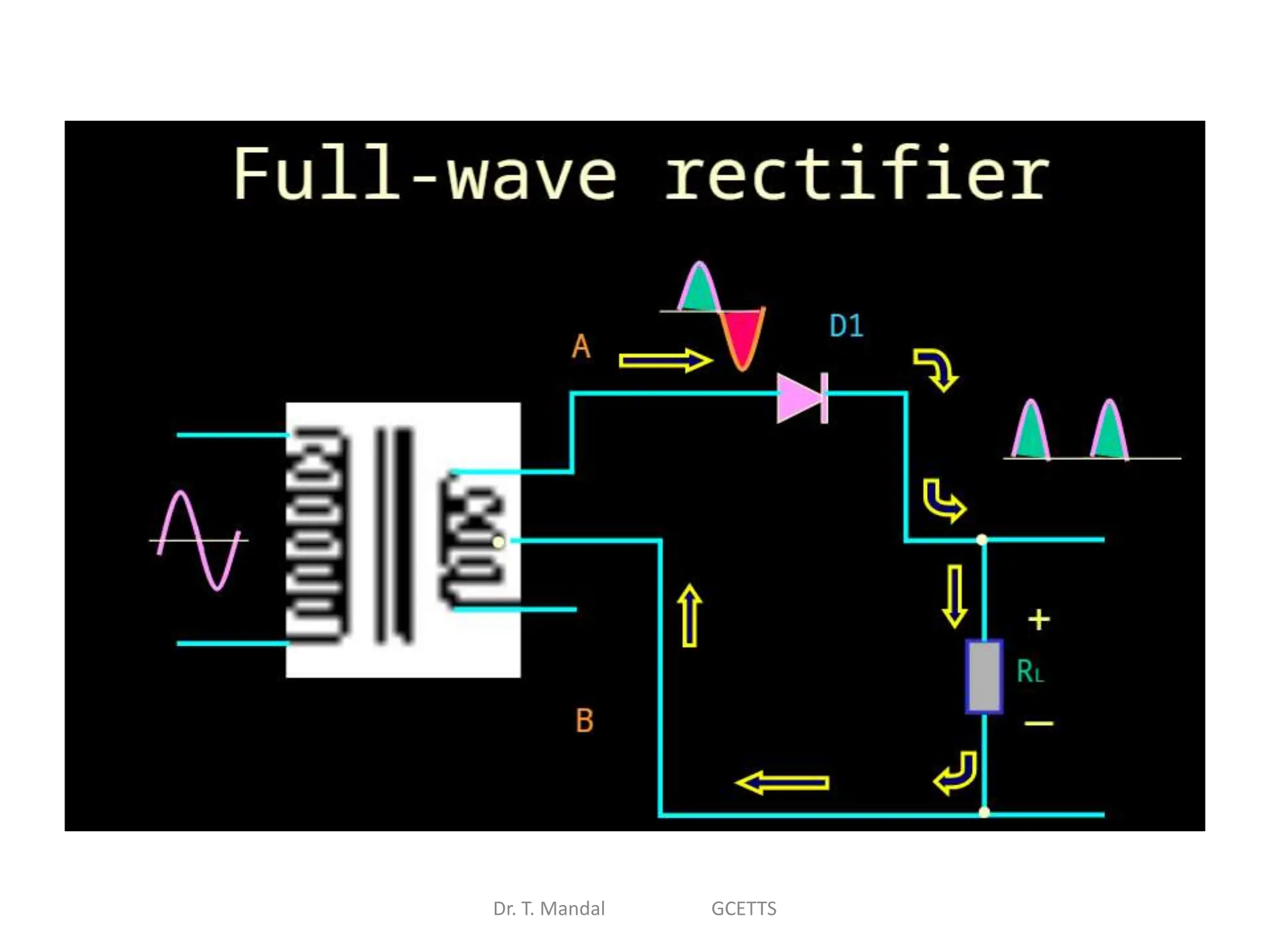
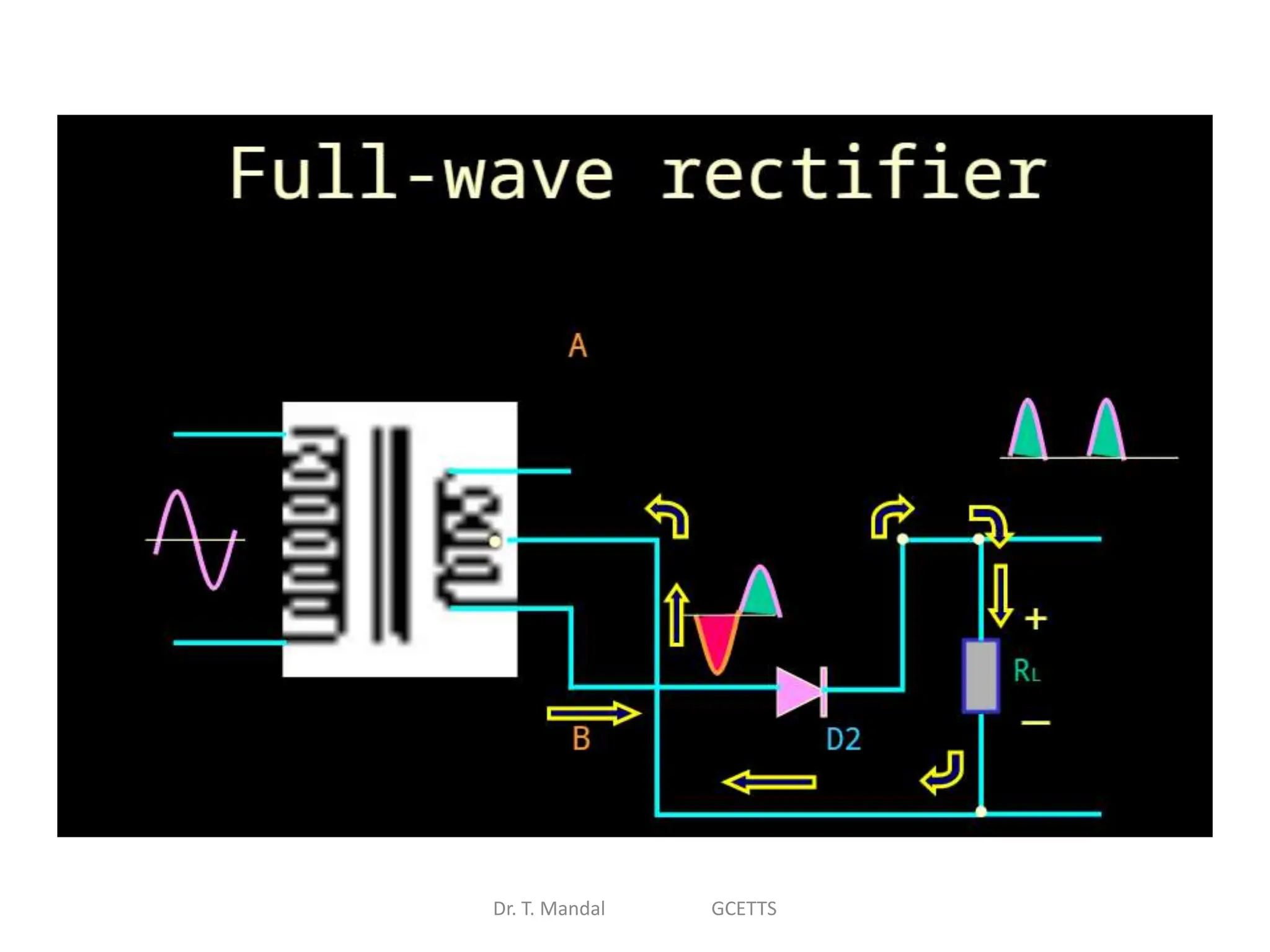
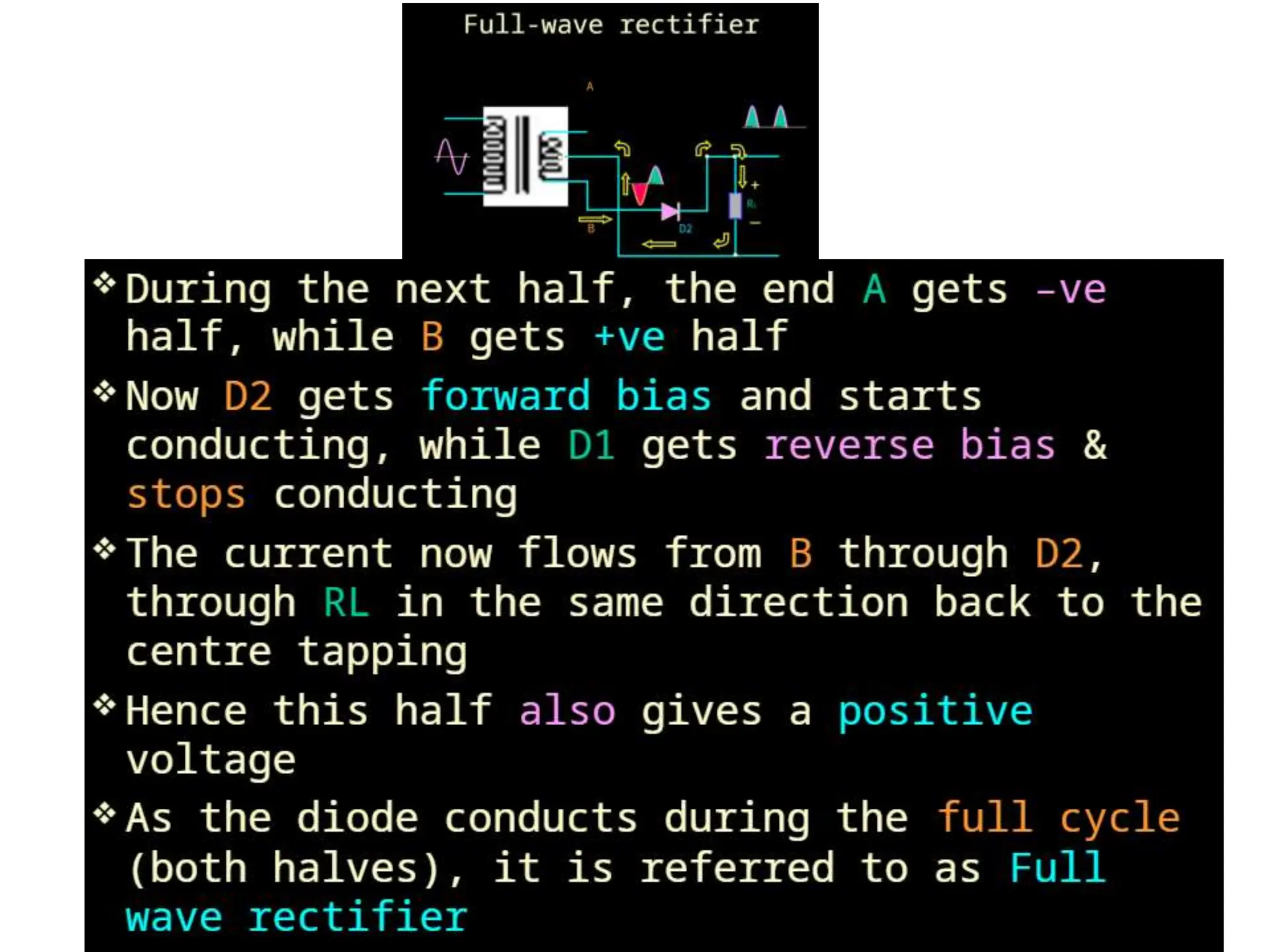
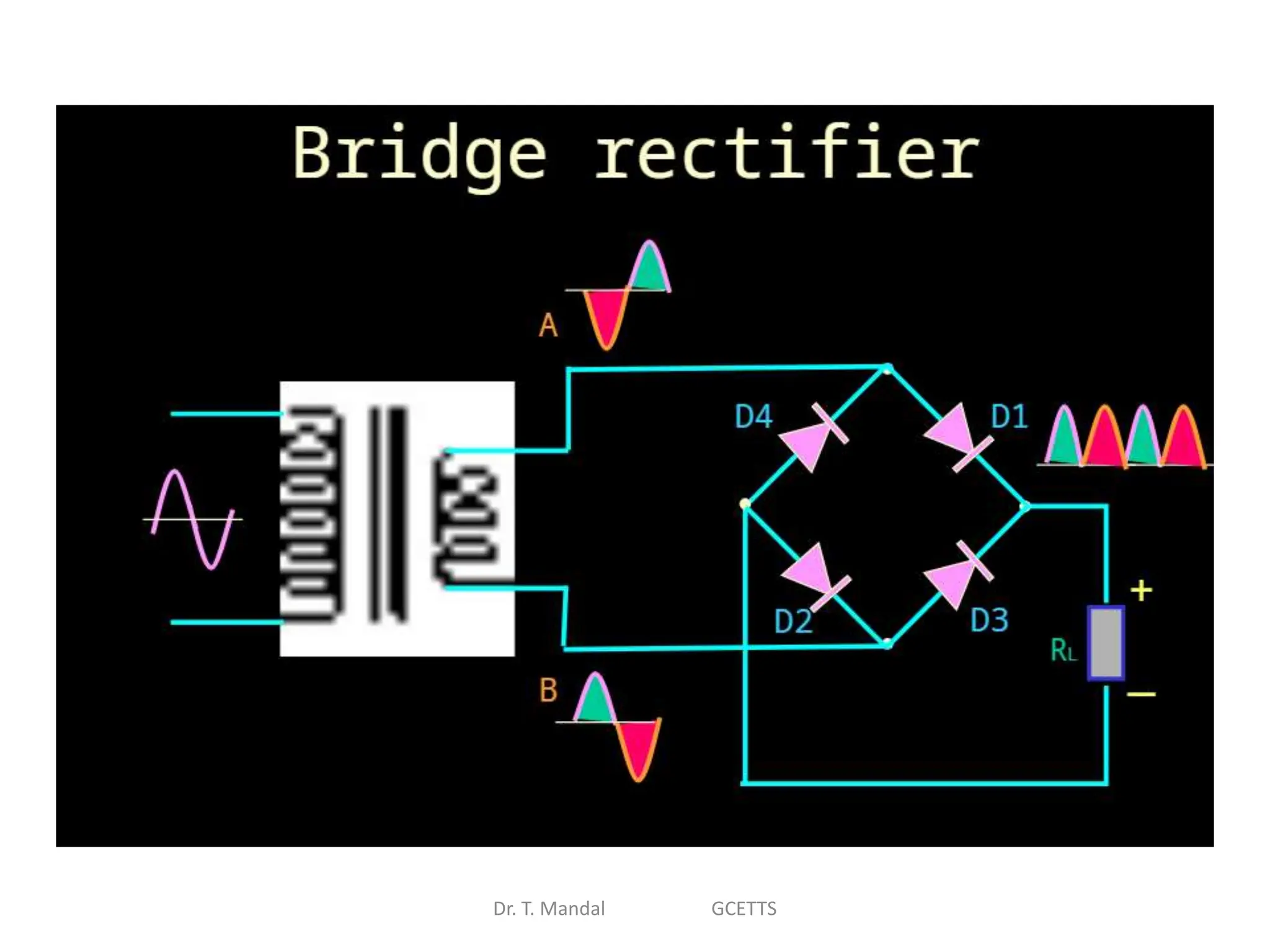
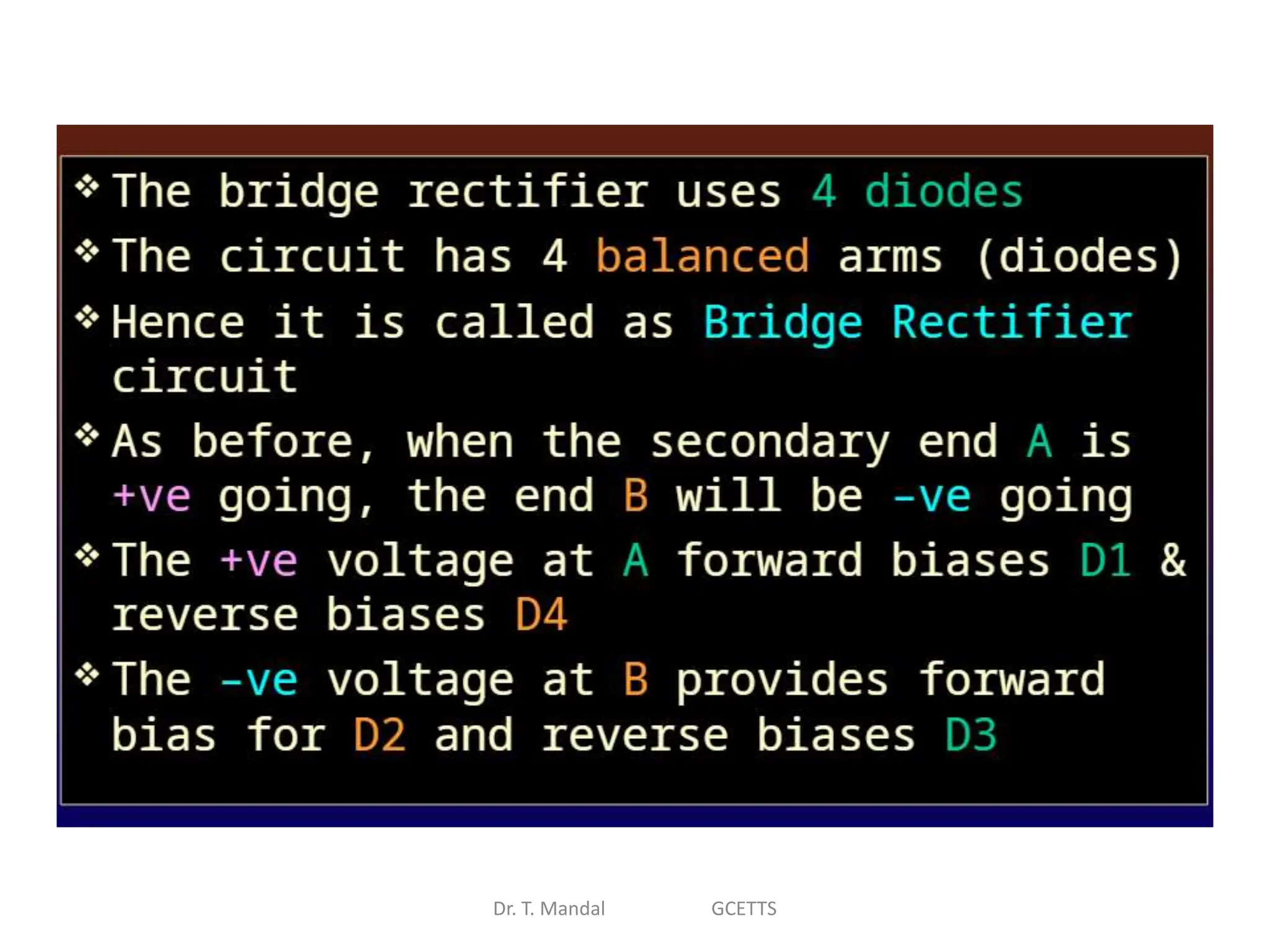
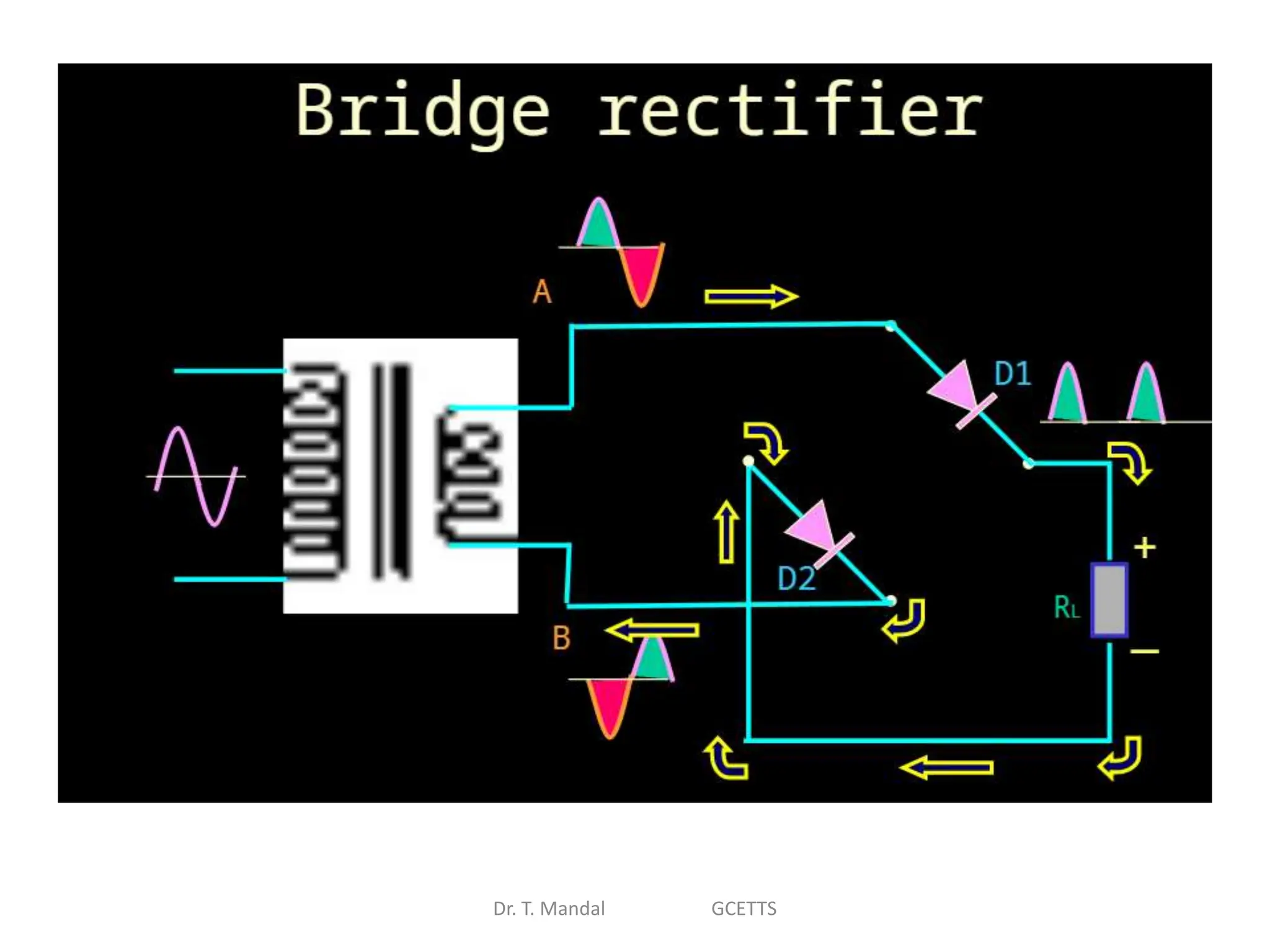
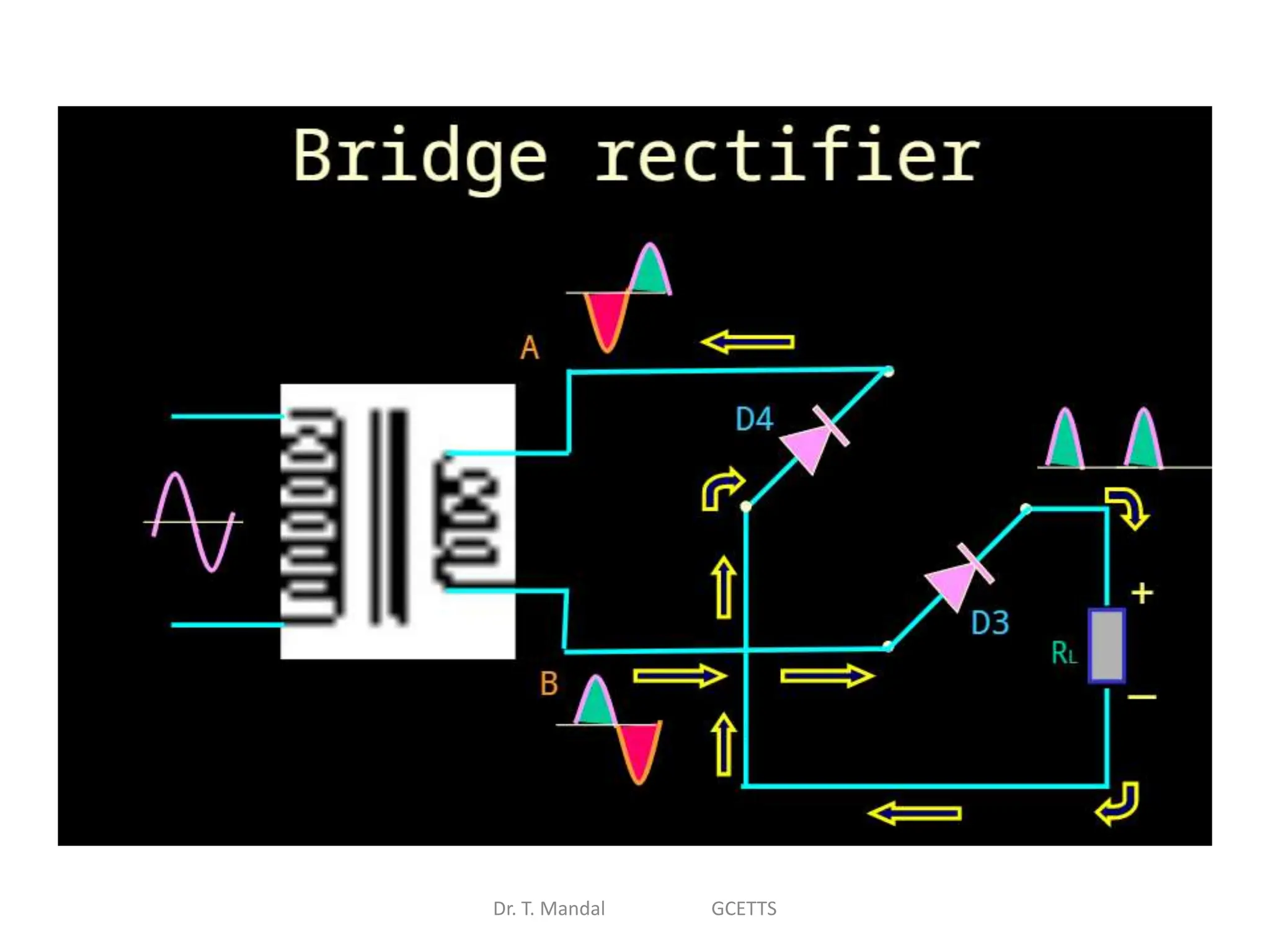
The document discusses fundamental concepts of digital logic, covering binary operators, closure properties, and Boolean algebra. It includes postulates, theorems, and methods for simplifying Boolean functions, as well as the roles of canonical and standard forms in expressing Boolean functions. Additionally, it describes combinational circuits, specifically adders and subtractors, and their truth tables.