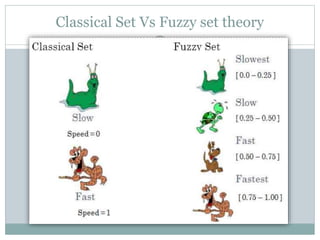
The document discusses fuzzy sets and fuzzy logic. It defines fuzzy as meaning not clear or precise, with blurred outlines. Fuzzy sets allow partial membership in a set, whereas classical sets have binary membership. Fuzzy sets are represented by membership functions that can take on values between 0 and 1. Common fuzzy set operations like union, intersection, and complement are defined. Fuzzy logic is then introduced as a way to represent imprecise concepts and approximate reasoning, extending conventional binary logic to allow intermediate truth values.

2. What is Fuzzy?
 Fuzzy means
 not clear, distinct or precise;
 not crisp (well defined);
 blurred (with unclear outline).

3. Sets Theory
 Classical Set: An element either belongs
or does not belong to a sets that have
been defined.
 Fuzzy Set: An element belongs partially
or gradually to the sets that have been
defined.

4. Classical Set Vs Fuzzy set theory

5. Classical Set theory
 Classical set theory represents all items elements,
A={ a1,a2,a3,…..an}
if elements ai (i=1,2,3,…n) of a set A are subset of
universal set X, then set A can be represent for all elements
x Є X by its characteristics function,
1
μA(x) =
{0
if x Є X
otherwise
thus in classical set theory μA(x) has only values 0
(false) and 1( true). Such set are called crisp sets

6. Fuzzy Set Theory
 Fuzzy set theory is an extension of classical set
theory where element have varying degrees of
membership. A logic based on the two truth values,
True and false, is sometimes inadequate when
describing human reasoning. Fuzzy logic uses the
whole interval between 0 and 1 to describe human
reasoning.
 A fuzzy set is any set that allows its members to have
different degree of membership, called membership
function, in the interval [0,1].

7. Definition
 A fuzzy set A, defines in the universal space X, is a function
defined in X which assumes values in range [0,1].
 A fuzzy set A is written as s set of pairs { x, A(x)} as
A= {{x, A(x)}}, x in the set X.
where x is element of universal space or set X and
A(x) is the value of function A for this element.
 Example: Set SMALL in set X consisting natural numbers
<= 5.
 Assume: SMALL(1)=1, SMALL(2)=1, SMALL(3)=0.9,
SMALL(4)=0.6, SMALL(5)=0.4
 Then set SMALL={ {1,1,},{2, 1},{3,0. 9},{4,0.6}, {5,0.4}}

8. Fuzzy V/s Crisp set
Yes

Is water colourless?
Crisp
No
Extremely
honest(1)
Very
honest(0.85)
Is Ram honest?
Fuzzy
Honest at
time (0.4)
Extremely
dishonest(0)

9. Fuzzy operations

10. Union
 The union of two fuzzy sets A and B is a new fuzzy set A U B
also on X with membership function defined as
μ A U B (x)= max (μ A (x) ,μ B (x))
 Example:
Let A be the fuzzy set of young people and B be the fuzzy set of
middle-aged people. In discrete form,
A=P(x1,0.5), (x2,0.7), (x3,0)} and B={(x1,0.8),( x2,0.2),( x3,1)}
So find out A U B .

11. Use formula
μ A U B (x1)= max (μ A (x1) ,μ B (x1))
= max(0.5,0.8)
=0.8
μ A U B (x2)= max (μ A (x2) ,μ B (x2))
= max(0.7,0.2)
=0.7
μ A U B (x3)= max (μ A (x3) ,μ B (x3))
= max(0,1)
=1
So,
A U B= {(x1,0.8, x2,0.7, x3,1)}

12. Intersection
U
 The union of two fuzzy sets A and B is a new fuzzy set A
B
also on X with membership function defined as
μ A B (x)= min (μ A (x) ,μ B (x))
 Example:
Let A be the fuzzy set of young people and B be the fuzzy set of
middle-aged people. In discrete form,
A=P(x1,0.5), (x2,0.7), (x3,0)} and B={(x1,0.8),( x2,0.2),( x3,1)}
So find out A B .
U
U

13. Use formula
μ A B (x1)= min (μ A (x1) ,μ B (x1))
= max(0.5,0.8)
=0.5
U
B (x2)=
U
μA
U
μA
min (μ A (x2) ,μ B (x2))
= max(0.7,0.2)
=0.2
B (x3)=
min (μ A (x3) ,μ B (x3))
= max(0,1)
=0
So,
A B= {(x1,0.5, x2,0.2, x3,0)}
U

14. Complement
 The complement of a fuzzy set A with membership function
defined as
μ A (x)= 1-μ A (x)
 Example:
Let A be the fuzzy set of young people complement “not
young” is defined as Ac. In discrete form, for x1, x2, x3
A=P(x1,0.5), (x2,0.7), (x3,0)}
So find out Ac.

15. Use formula
μ A (x1)= 1- μ A (x1 )
= 1-0.5
=0.5
μ A (x1)= 1- μ A (x1 )
= 1-0.7
=0.3
μ A (x1)= 1- μ A (x1 )
= 1-0
=1
So,
Ac= {(x1,0.5, x2,0.3, x3,1)}

16. Product of two fuzzy set
 The product of two fuzzy sets A and B is a new fuzzy set A .B
also on X with membership function defined as
μ A.B (x)= μ A (x) μ B (x)
 Example:
Let A be the fuzzy set of young people and B be the fuzzy set of
middle-aged people. In discrete form,
A=P(x1,0.5), (x2,0.7), (x3,0)} and B={(x1,0.8),( x2,0.2),( x3,1)}
So find out A.B

17. Use formula
μ A .B (x1)= μ A (x1).μ B (x1)
= 0.5 . 0.8
=0.040
μ A .B (x2)= μ A (x2).μ B (x2)
= 0.7 . 0.2
=0.014
μ A .B (x3)= μ A (x3).μ B (x3)
=0 . 1
=0
So,
A .B= {(x1,0.040, x2,0.014, x3,0)}

18. Equality
 The two fuzzy sets A and B is said to be equal(A=B) if
μ A (x) =μ B (x)
 Example:
A=(x1,0.2), (x2,0.8)}
B={(x1,0.6),( x2,0.8)}
C={(x1,0.2),( x2,0.8)}
μ A (x1) ≠μ B (x1) & μ A (x2) =μ B (x2)
μ A (0.2) ≠μ B (0.6) & μ A (0.8) =μ B (0.8)
so, A≠B
μ A (x1) =μ c (x1) & μ A (x2) =μ c (x2)
μ A (0.2) =μ c (0.2) & μ A (0.8) =μ c (0.8)
so, A=C

19. Fuzzy Logic
 Flexible machine learning technique
 Mimicking the logic of human thought
 Logic may have two values and represents two
possible solutions
 Fuzzy logic is a multi valued logic and allows
intermediate values to be defined
 Provides an inference mechanism which can
interpret and execute commands
 Fuzzy systems are suitable for uncertain or
approximate reasoning

20. Fuzzy Logic
 A way to represent variation or imprecision in logic
 A way to make use of natural language in logic
 Approximate reasoning
 Definition of Fuzzy Logic:
A form of knowledge representation suitable for
notions that cannot be defined precisely, but which
depend upon their contexts.
 Superset of conventional (Boolean) logic that has
been extended to handle the concept of partial truth the truth values between "completely true &
completely false".

21. Fuzzy Propositions
A fuzzy proposition is a statement that drives a fuzzy
truth value.
 Fuzzy Connectives: Fuzzy connectives are used
to join simple fuzzy propositions to make
compound propositions. Examples of fuzzy
connectives are:
 Negation(-)
 Disjunction(v)
 Conjunction(^)
 Impication( )

23. Example