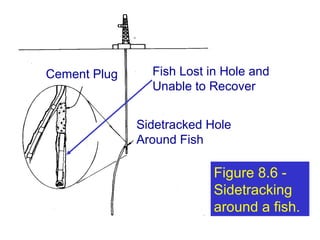
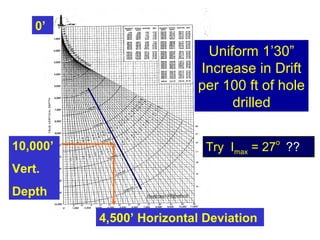
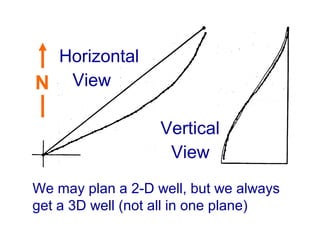
Directional drilling is the process of directing a wellbore along a non-vertical trajectory towards a predetermined target. It involves techniques like whipstocks, jet bits, and downhole motors to gradually build angle in the wellbore. There are three main types of directional well paths: Type I involves continuously building angle to a maximum and then holding; Type II involves building, holding, and dropping the angle; Type III only involves continuously building angle. Survey calculation methods like the average angle method are used to determine the wellbore position between survey points by calculating average inclination and azimuth angles.

1. Petroleum Engineering 406
Lesson 18
Directional Drilling

2. Lesson 10 - Directional Drilling
 When is it used?
 Type I Wells (build and hold)
 Type II Wells (build, hold and drop)
 Type III Wells (build)
 Directional Well Planning & Design
 Survey Calculation Methods

3. Homework:
READ. “Applied Drilling Engineering”
Ch. 8, pp. 351-363
REF. API Bulletin D20, “Directional Drilling
Survey Calculation Methods and
Terminology”

4. What is Directional Drilling?
Directional Drilling is the process of
directing a wellbore along some trajectory
to a predetermined target.
Basically it refers to drilling in a non-vertical
direction. Even “vertical” hole sometimes
require directional drilling techniques.
Examples: Slanted holes, high angle holes (far from vertical), and Horizontal holes.

5. North
Direction
Angle
Direction Plane X
Inclination Angle
Z Axis (True Vertical
Depth)Inclination
Plane Y
θ, α or I
φ, ε or
A
Non-Vertical
Wellbore

6. Figure 8.2 - Plan view of a typical oil and gas structure under a lake showing how
directional wells could be used to develop it. Best locations? Drill from lake?
Lease Boundary
Surface Location for Well No. 1
Bottom Hole Location for Well 2
Surface
Location for
Well No. 2
Houses
Oil-Water
Contact

7. Figure 8.3 - Typical offshore development platform
with directional wells.
NOTE: All the
wells are
directional
Top View
5 - 50 wells
per platform

8. Figure 8.4 - Developing a field under a city
using directionally drilled wells.
Drilling Rig Inside Building

9. Fig. 8.5 - Drilling of directional wells where the
reservoir is beneath a major surface obstruction.
Why not
drill from
top of
mountain?
Maximum
lateral
displ.?

10. Figure 8.6 -
Sidetracking
around a fish.
Sidetracked Hole
Around Fish
Fish Lost in Hole and
Unable to Recover
Cement Plug

11. Figure 8.7 -
Using an old
well to explore
for new oil by
sidetracking
out of the
casing and
drilling
directionally.
Possible
New Oil
Sidetracked
Out of Casing
Oil Producing Well
Ready to Abandon
Old Oil Reservoir

12. Figure 8.8 - Major types of wellbore trajectories.
Build and
Hold Type
Continuous
Build
Build-hold Drop and/or Hold
(Modified “S” Type)
Build-hold and Drop (“S Type”)
Horizontal
Departure
to Target
Type I
Type III
Type II

13. Figure 8.10 -
Geometry of the
build section.
Build Section
Build Radius:
BUR*
,
π
=
00018
r1

14. Build Section:
↑↑
==
−==
==
=
degrad
180
*
100L
r
)cos(1rDD'dev.Horiz.
sinrD'C'depthicalVert
rLarc,ofLength
1
1
1
1
11
11
111
π
θθ
θ
θ
θ
BUR*
,
π
=
00018
r1

15. Build-hold-and drop for the case where:
42131 xrrandxr <+<
Target
Drop Off
End of Build
Start of Buildup
Type II

16. Build-hold-and
drop for the case
where:
Kickoff
End of Build
Maximum
Inclination
Angle
Drop Off
Target
42131 xrrandxr >+<
Type II

17. Fig. 8-14. Directional well used to intersect
multiple targets
Target 1
Target 2
Target 3
Projected Trajectory Projected Trajectory
with Left Turn to Hit
Targets

18. Fig. 8-15.
Directional
quadrants and
compass
measurements
N18E S23E
A = 157
o
N55W
A = 305
o
S20W

19. Figure 8-16: Plan View
Lead Angle
Lake
Surface
Location
for Well
No. 2
Projected Well Path
Target at a
TVD 9,659

20. Example 1: Design of
Directional Well
Design a directional well with the following
restrictions:
Total horizontal departure = 4,500 ft
True vertical depth (TVD) = 12,500 ft
Depth to kickoff point (KOP) = 2,500 ft
Rate of build of hole angle = 1.5 deg/100 ft

21. Example 1: Design of
Directional Well
This is a Type I well (build and hold)
(i) Determine the maximum hole
angle (inclination) required.
(ii) What is the total measured depth
of the hole (MD)?

22. 2500’
10,000’
Imax
Imax
TVD1
4,500’
12,500’
Type I: Build-and-Hold
HD1

23. Uniform 1’30”
Increase in Drift
per 100 ft of hole
drilled
10,000’
Vert.
Depth
4,500’ Horizontal Deviation
0’
Try Imax = 27
o
??

25. Solution
Type I Well 1.5 deg/100’
2500’ Available depth
= 12,500-2,500
= 10,000’
10,000’
Imax
Imax
From Chart,
Try = 27
o
Imax
TVD1
HD1

26. Build Section
Imax
Imax
TVD1
HD1
MD1 = 1,800’ (27/1.5)
TVD1 = 1,734’
HD1 = 416’
Remaining vertical height
= 10,000 - 1,734 = 8,266’
From chart of 1.5 deg/100’, with Imax = 27o
In the BUILD Section:
8,266’

27. Solution
Horizontally:
416 + 8,266 tan 27
o
= 4,628
We need 4,500’ only:
Next try Imax = 25’ 30 min
Imax8,266’
MD2 = 1,700’ (25.5/1.5)
TVD2 = 1,644’
HD2 = 372’

28. Solution:
Remaining vertical depth = 10,000-1644
= 8,356 ft.
∴ Horizontal deviation = 372+8,356 tan 25.5
= 4,358 ft. { <4500 }
Approx. maximum angle = 26
What is the size of target?
4
10

29. MD = MDvert + MDbuild + MDhold
13,500'MD
13,458'
25.5cos
8,356
1,7002,50025.5atMD
13,577'
27cos
266,8
'800,1'500,227atMD
≅∴
=
++=
=
++=




30. Type II Pattern
Given: KOP = 2,000 feet
TVD = 10,000 feet
Horiz. Depart. = 2,258 feet
Build Rate = 20
per 100 feet
Drop Rate = 10
30’ per 100 feet
The first part of the calculation is the
same as previously described.

31. Procedure - Find:
 a) The usable depth (8,000 feet)
 b) Maximum angle at completion of
buildup (180
)
 c) Measured depth and vertical depth at
completion of build up
(M.D.=900 ft. and TVD = 886)
 d) Measured depth, horizontal departure
and TVD for 1 /100 ft from chart.
0
2
1

32. Solve:
 For the distances corresponding to the
sides of the triangle in the middle.
 Add up the results.
 If not close enough, try a different value
for the maximum inclination angle, Imax

33. Example 1: Design of Directional
Well
(i) Determine the maximum hole angle
required.
(ii) What is the total measured depth (MD)?
(MD = well depth measured along the
wellbore,
not the vertical depth)

34. (i) Maximum
Inclination
Angle
r1 =
18 000
15
,
. π
0r2 =
( )D4 1
12 500 2 500
10 000
−
= −
=
D
ft
, ,
,

35. (i) Maximum Inclination Angle








−
−+−
=








−+
+−−+−−
= −
500,4)820,3(2
500,4)820,3(2000,10500,4000,10
tan2
x)rr(2
x)rr(2)DD(xDD
tan2
22
1-
421
421
2
14
2
4141
maxθ

3.26max =θ

36. (ii) Measured Depth of Well
ft265,9L
105,4sinL
ft4,105
395500,4x
ft395
)26.3cos-3,820(1
)cos1(rx
Hold
Hold
Hold
1Build
=∴
=∴
=
−=∴
=
=
−=
θ
θ


37. (ii) Measured Depth of
Well
265,9
180
26.3
3,8202,500
LrDMD Holdrad11
+





+=
++=
π
θ
ft518,13MD =

38. We may plan a 2-D well, but we always
get a 3D well (not all in one plane)
Horizontal
Vertical
ViewN
View

39. Fig. 8-22. A curve representing a wellbore
between survey stations A1 and A2
MD, α1, ε1
∆MD
α2, ε2
β = dogleg
angle

40. Directional Drilling
 1. Drill the vertical (upper) section of
the hole.
 2. Select the proper tools for kicking off
to a non-vertical direction
 3. Build angle gradually

41. Directional Tools
 (i) Whipstock
 (ii) Jet Bits
 (iii) Downhole motor and bent sub

42. Whipstocks
Standard retreivable Circulating Permanent Casing

43. Setting a Whipstock
 Small bit used to start
 Apply weight to:
– set chisel point &
– shear pin
 Drill 12’-20’
 Remove whipstock
 Enlarge hole

44. Jetting Bit
 Fast and
economical
 For soft formation
 One large - two
small nozzles
 Orient large nozzle
 Spud periodically
 No rotation at first
Small Jets

45. Jetting
 Wash out pocket
 Return to normal
drilling
 Survey
 Repeat for more
angle if needed

46. Mud Motors
Drillpipe
Non-magnetic
Drill Collar
Bent Sub
Mud Motor
Rotating
Sub

48. Increasing Inclination
 Limber assembly
 Near bit stabilizer
 Weight on bit forces
DC to bend to low
side of hole.
 Bit face kicks up

49. Hold Inclination
 Packed hole
assembly
 Stiff assembly
 Control bit weight
and RPM

50. Decrease Inclination
 Pendulum effect
 Gravity pulls bit
downward
 No near bit stabilizer

51. Packed Hole Assemblies
Drill
pipe
HW DP
String
Stabilizer
Steel DC
String
Stabilizer
String
Stabilizer
Monel
DCSteel DC
NB
Stab

52. Vertical Calculation Horizontal Calculation

53. 3D View Dog Leg Angle

54. Deflecting Wellbore Trajectory
0
90
180
270

55. Bottom Hole Location
10,000:TVD
ft2,550:Distance
E53N:Direction 
o1-
22
53
N
E
tanDirectionClosure
NE2,550Closure
ft1,535
53cos2,550N
ft2,037
53sin550,2E
=





=
+==
=
=
=
=



56. Survey Calculation Methods
1. Tangential Method
= Backward Station Method
= Terminal Angle Method
Assumption: Hole will maintain
constant inclination and azimuth
angles between survey points

57. BAB
BAB
BA
BA
IsinABH
IcosABV:nCalculatio
A,AAngles
I,IesAngl
ABDistance
AofLocation:Known
=
=
Poor accuracy!!
A
B
IA
IB
IB

58. Average Angle Method
= Angle Averaging Method
Assumption: Borehole is parallel to the
simple average drift and bearing angles
between any two stations.
Known: Location of A, Distance AB,
Angles BABA A,A,I,I

59. (i) Simple enough for field use
(ii) Much more accurate than
“Tangential” Method
A
B
IA
IB
IAVG
IAVG





 +
=
2
II
I BA
avg





 +
=
2
AA
A BA
avg

60. Average Angle Method
Vertical Plane:
A
B
IA
IB
IAVG
IAVG





 +
=
2
II
I BA
avg
avgAB
avgAB
IsinABH
IcosABV
=
=

61. Average Angle Method
Horizontal Plane:
avg
avgavg
avgavg
IcosABZ
AcosIsinABN
AsinIsinABE
=∆
=∆
=∆
N
B
AA
AB
AAVG
E
∆E
∆N
A
avgAB IsinABH =

62. Change in position towards the east:
Change in position towards the north:
)1..(
2
AA
sin
2
II
sinLEx BABA





 +





 +
=∆=∆
)2..(
2
AA
cos
2
II
sinLNy BABA





 +





 +
=∆=∆
)3..(
2
II
cosLZ BA





 +
=∆
Change in depth:
Where L is the measured distance
between the two stations A & B.

63. Example
The coordinates of a point in a wellbore
are:
x = 1000 ft (easting)
y = 2000 ft (northing)
z = 3000 ft (depth)
At this point (station) a wellbore survey shows
that the inclination is 15 degrees from vertical,
and the direction is 45 degrees east of north. The
measured distance between this station and the
next is 300 ft….

64. Example
The coordinates of point 1 are:
x1 = 1000 ft (easting)
y1 = 2000 ft (northing) I1 = 15
o
z1 = 3000 ft (depth) A1 = 45
o
L12 = 300 ft
At point 2, I2 = 25
o
and A2 = 65
o
Find x , y and z

65. Solution
H12 = L12 sin Iavg = 300 sin 20 = 103 ft
∆E = H12 sin Aavg = 103 sin 55 = 84 ft
∆N = H12 cos Aavg = 103 cos 55 = 59 ft
∆Z = L12 cos Iavg = 300 cos 20 = 282 ft
20
2
2515
2
II
I 21
avg =




 +
=




 +
=
55
2
6545
2
AA
A 21
avg =




 +
=




 +
=

66. Solution - cont’d
∆E = 84 ft
∆N = 59 ft
∆Z = 282 ft
x2 = x1 + ∆E = 1,000 + 84 ft = 1,084 ft
y2 = y1 + ∆N = 2,000 + 59 ft = 2,059 ft
z2 = z1 + ∆Z = 3,000 + 282 ft = 3,282 ft