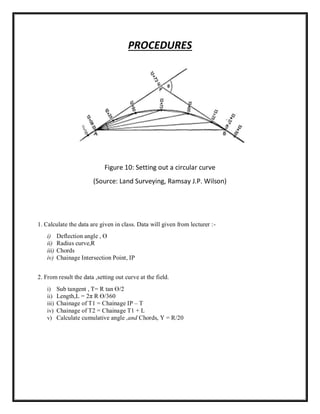
The document is a field work report for a surveying exercise to set out a ranging curve. It includes information on the materials and tools used, two methods for setting out the curve (offset from tangent line and using deflection angles), and results including calculation data and tables of station coordinates, chords, and deflection angles. The objectives were to calculate data for a given curve, set it out in the field using total station, and analyze the results.

1. CIVIL ENGINEERING DEPARTMENT
DCC 20063
ENGINEERING SURVEY
FIELD WORK REPORT
FIELD WORK TITLE
RANGING CURVE
NAME MUHAMMAD MUAZZAM BIN MAZLAN
REG NUMBER 03DKA21F2013
MEMBER OF GROUP
MOHAMMAD FARHAT BIN SUHAIMI CRITERIA MARK
MUHAMAD SUFYAN IZZUDINBIN MUHAMAD SUHAIMI INTRODUCTION
/5
MATERIALS AND METHODS
/5
DATA
/5
PLOTTING
/5
ANALYSIS
/5
DISCUSSION
/5
CONCLUSION
/5
COURSE/SESSION
DKA SESSION 1 2022/2023
TOTAL MARK
LECTERUR SAMSUL NIZAN BIN MOHD EHSAN COMMENT:

2. FIELD WORK 4 : RANGING CURVE
INTRODUCTION
Curves are frequent bends in communication lines such
as roads, trains, and canals that cause a progressive
change in direction. They are also employed in the
vertical plane at all grade changes to avoid a sudden
change in slope at the apex.
Horizontal curves are those that are supplied in the
horizontal plane to have a progressive change in
direction, whilst vertical curves are those that are offered
in the vertical plane to have a gradual change in grade.
Curves are drawn on the ground along the work's centre
line. They can be either circular or parabolic.

3. MATERIALS AND TOOLS
TOTAL STATION
TRIPOD HAMMER PRISM
PICKET
FIELD BOOK/BOOKING
FORM
RANGING POLE SURVEYING ARROW

4. NO TOOLS QUANTITY
1 Total station 12
2 Tripod 1
3 Hammer 1
4 Prism 1
5 Picket 12
6 Surveying Arrow 12
7 Ranging Pole 2
8 Field book/booking form 1

5. METHOD 1
OFFSET FROM TANGENT LINE

6. PROCEDURE
1. Calculate the data are given in class. Data will given from lecturer :-
i) Deflection angle, Ө
ii) Radius curve, R
iii) Chords
iv) Chainage Intersection Point, IP
2. From result the data setting out curve at the field.
i) Sub tangent, 𝑇 = 𝑅 tan
𝜃
2
ii) Length, 𝐿 = 2𝜋𝑅
𝜃
360
iii) Chainage of Tı =Chainage IP-T
iv) Chainage of T2 -Chainage Ti +L
v) Calculate X1, X2, Y3 and etc……,and Chords, 𝑌 =
𝑅
20
y = R -
Y R R 2
− X 2
R2
− X 2
X
3. Plot the diagram.
4. Choose appropriate intersection point , IP in the line and mark the tangent line likes T1 , T2 and IP
with ranging pole. Mark the tangent distance T1- IP
5. From Y1 measure the distance of X1 , and setting to IP in the tangent line. Using optical square at
point Y1 measure the X1 mark the point with surveying arrow.
6. Repeat procedure ( 5 ) for remaining points.
R 2
− X 2

7. METHOD 2
CIRCULAR CURVE USING DEFLECTION ANGLE

8. PROCEDURES
Figure 10: Setting out a circular curve
(Source: Land Surveying, Ramsay J.P. Wilson)
1. Calculate the data are given in class. Data will given from lecturer :-
i) Deflection angle , Ө
ii) Radius curve,R
iii) Chords
iv) Chainage Intersection Point, IP
2. From result the data ,setting out curve at the field.
i) Sub tangent , T= R tan Ɵ/2
ii) Length,L = 2π R Ɵ/360
iii) Chainage of T1 = Chainage IP – T
iv) Chainage of T2 = Chainage T1 + L
v) Calculate cumulative angle ,and Chords, Y = R/20

9. DEFLECTION ANGLE , Ө =
𝟏𝟕𝟏𝟖.𝟗 𝑪
𝑹
60 ՜
1. Plot the diagram.
2. Observation of the area.
3. Mark the intersection point IP and used total station to set the angle of intersection to determine
the points T1 and T2.
4. Transfer and set up the Total Station at point T1.
5. Open the first deflection angle (∂1) and determined the distance C1 according to the table.
6. Mark point A with the arrow.
7. Open the first deflection angle (∂2) and determined the distance C2
8. Mark point A with the arrow.
9. Repeat the same process to set out the remaining pegs.
10. Continue until the last peg on the curve has been placed and measure the remaining distance to
T2 which should equalthe calculated length c" of the final sub-chord. Also set out the final
deflection angle, which should pass through tangent point T2, indicating no disturbance of the
instrument.
11. As a final check on the accuracy, locate point T2 by the deflection angle and sub-chord c". If
this position does not coincide with the tangent point T2, the distance between the two is the
actual error of tangency. If this is large, indicating an error, the whole process must be
repeated. Where calculations are inaccurate by a few millimeters in thefinal placing of the pegs,
it is usual to adjust the last few pegs to secure tangency.
Station Chainage Chords
C
Deflection angle
, ∂
∂ Cumulative
@
𝟐𝟖.𝟔𝟒𝟖𝟑 𝑪
𝑹

10. RESULT AND ANALYSIS DATA

11. METHOD 1 : OFFSET FROM TANGENT LINE
X = R -
Y R R 2 − X 2
√R 2 − X 2
X REMARKS
0.000 100.000 10000.000 100.000 0.000 T1
5.000 100.000 9975.000 99.875 0.125 A
10.000 100.000 9900.000 99.499 0.501 B
15.000 100.000 9775.000 98.869 1.131 C
20.000 100.000 9600.000 97.980 2.020 D
25.000 100.000 9375.000 96.825 3.175 E
27.112 100.000 9264.939 96.255 3.745 lP
0.000 0.000 0.000
0.000 0.000 0.000
0.000 0.000 0.000
0.000 0.000 0.000
0.000 0.000 0.000
0.000 0.000 0.000
0.000 0.000 0.000
0.000 0.000 0.000
0.000 0.000 0.000
0.000 0.000 0.000
0.000 0.000 0.000
0.000 0.000 0.000
0.000 0.000 0.000

12. METHOD 2 - CIRCULAR CURVE USING
DEFLECTION ANGLE
STATION CHAINAGE CHORDS DEFLECTION
ANGLE,
∂
CUMULATIVE
∂
T1 72.888 0.000 0°00’00’’ 0°00’00’’
A 77.888 5.000 1°25’56.64’’ 1°25’56.64’’
B 82.888 5.000 1°25’56.64’’ 2°51’53.28’’
C 87.888 5.000 1°25’56.64’’ 4°17’49.92’’
D 92.888 5.000 1°25’56.64’’ 5°43’46.92’’
E 97.888 5.000 1°25’56.64’’ 7°9’43.56’’
F 102.888 5.000 1°25’56.64’’ 8°35’40.2’’
G 107.888 5.000 1°25’56.64’’ 10°1’36.84’’
H 112.888 5.000 1°25’56.64’’ 11°27’33.48’’
J 117.888 5.000 1°25’56.64’’ 12°53’30.12’’
K 122.888 5.000 1°25’56.64’’ 14°19’27.12’’
T2 125.839 2.951 0°50’43.44’’ 15°10’10.56’’

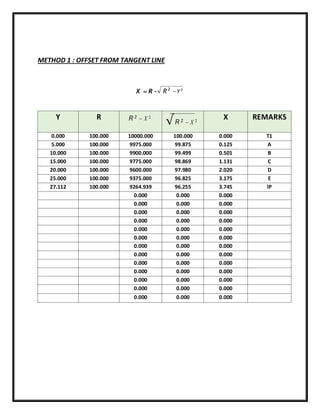
13. CALCULATION DATA OFFSET FROM TANGENT LINE
𝜃 = 30°20′20′′
J = 100 m
IP = 100 m
C = 5 m
𝑱𝟐
− 𝒀𝟐
FOR T1
= 𝟏𝟎𝟎. 𝟎𝟎𝟎𝟐
− 𝟎. 𝟎𝟎𝟎𝟐
= 10000.000
𝑱𝟐
− 𝒀𝟐
𝑭𝑶𝑹 𝑨
= 𝟏𝟎𝟎. 𝟎𝟎𝟎𝟐 − 𝟓. 𝟎𝟎𝟎𝟐
= 9975.000
√𝑱𝟐 + 𝒀𝟐 𝑭𝑶𝑹 𝑻𝟏
= √𝟏𝟎𝟎. 𝟎𝟎𝟎𝟐 + 𝟎. 𝟎𝟎𝟎𝟐
= 𝟏𝟎𝟎. 𝟎𝟎𝟎
√𝑱𝟐 + 𝒀𝟐 𝑭𝑶𝑹 𝑨
= √𝟏𝟎𝟎. 𝟎𝟎𝟎𝟐 + 𝟓. 𝟎𝟎𝟎𝟐
= 𝟗𝟗. 𝟖𝟕𝟓
𝑿 = 𝑱 − √𝑱𝟐 + 𝒀𝟐 𝑭𝑶𝑹 𝑻𝟏
= 𝟏𝟎𝟎. 𝟎𝟎𝟎 − 𝟏𝟎𝟎. 𝟎𝟎𝟎
= 𝟎. 𝟎𝟎𝟎
𝑿 = 𝑱 − √𝑱𝟐 + 𝒀𝟐 𝑭𝑶𝑹 𝑨
= 𝟏𝟎𝟎. 𝟎𝟎𝟎 − 𝟗𝟗. 𝟖𝟕𝟓
= 𝟎. 𝟏𝟐𝟓
𝑱𝑻 = 𝟏𝟎𝟎 𝒕𝒂𝒏
[𝟑𝟎°𝟐𝟎′𝟐𝟎′′]
𝟐
= 27.112 m
𝑳 = 𝟐 𝝅 (𝟏𝟎𝟎)[
𝟑𝟎°𝟐𝟎′
𝟐𝟎′′
𝟑𝟔𝟎°
]
= 𝟓𝟐. 𝟗𝟓 𝐦
𝑪 = 𝟐(𝟏𝟎𝟎) 𝒔𝒊𝒏 [
𝟑𝟎°𝟐𝟎′
𝟐𝟎′′
𝟐
]
= 𝟓𝟐. 𝟑𝟑 𝐦
T1 = 100 – 27.112
= 72.888 m
T2 = 72.888 + 52.95
= 125.839 m

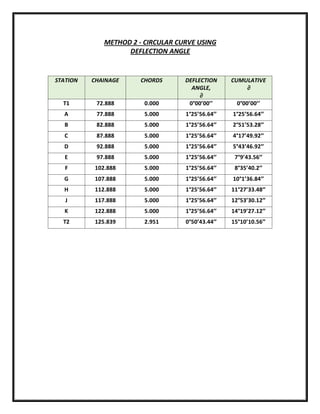
14. CALCULATION DATA CIRCULAR CURVE USING DEFLECTION ANGLE
𝜃 = 30°20′20′′
J = 100 m
IP = 100 m
C = 5 m
𝑰𝑷 𝑭𝑶𝑹 𝑨 = 𝟕𝟐. 𝟖𝟖𝟖 + 𝟓 = 𝟕𝟕. 𝟖𝟖𝟖
𝑰𝑷 𝑭𝑶𝑹 𝑩 = 𝟕𝟕. 𝟖𝟖𝟖 + 𝟓 = 𝟖𝟐. 𝟖𝟖𝟖
𝑫𝑬𝑭𝑳𝑬𝑪𝑻 𝑨𝑵𝑮𝑳𝑬, 𝜽 (𝑭𝑶𝑹 𝑨) → 𝟐𝟖.𝟔𝟒𝟖𝟑
𝑪
𝑹
= 𝟐𝟖.𝟔𝟒𝟖𝟑
(𝟓)
𝟏𝟎𝟎
= 𝟏°𝟐𝟓′
𝟓𝟔.𝟕𝟎′′
𝑫𝑬𝑭𝑳𝑬𝑪𝑻 𝑨𝑵𝑮𝑳𝑬, 𝜽 (𝑭𝑶𝑹 𝑻𝟐) → 𝟐𝟖.𝟔𝟒𝟖𝟑
𝑪
𝑹
= 𝟐𝟖.𝟔𝟒𝟖𝟑
(𝟐.𝟗𝟓𝟏)
𝟏𝟎𝟎
= 𝟎°𝟓𝟎′
𝟒𝟑.𝟒𝟖′′
𝑪𝑼𝑴𝑼𝑳𝑨𝑻𝑰𝑽𝑬 𝑨𝑵𝑮𝑳𝑬, 𝜽 (𝑭𝑶𝑹 𝑩)
= 𝟏. 𝟒𝟑𝟐𝟒 + 𝟏. 𝟒𝟑𝟐𝟒
= 𝟐. 𝟖𝟔𝟒𝟖
𝑪𝑼𝑴𝑼𝑳𝑨𝑻𝑰𝑽𝑬 𝑨𝑵𝑮𝑳𝑬, 𝜽 (𝑭𝑶𝑹 𝑪)
= 𝟐. 𝟖𝟔𝟒𝟖 + 𝟏. 𝟒𝟑𝟐𝟒
= 𝟒. 𝟐𝟗𝟕𝟐
𝑪𝑼𝑴𝑼𝑳𝑨𝑻𝑰𝑽𝑬 𝑨𝑵𝑮𝑳𝑬, 𝜽 (𝑭𝑶𝑹 𝑫)
= 𝟒. 𝟐𝟗𝟕𝟐 + 𝟏. 𝟒𝟑𝟐𝟒
= 𝟓. 𝟕𝟐𝟗𝟕
𝑱𝑻 = 𝟏𝟎𝟎 𝒕𝒂𝒏
[𝟑𝟎°𝟐𝟎′𝟐𝟎′′]
𝟐
= 27.112 m
𝑳 = 𝟐 𝝅 (𝟏𝟎𝟎)[
𝟑𝟎°𝟐𝟎′
𝟐𝟎′′
𝟑𝟔𝟎°
]
= 𝟓𝟐. 𝟗𝟓 𝐦
𝑪 = 𝟐(𝟏𝟎𝟎) 𝒔𝒊𝒏 [
𝟑𝟎°𝟐𝟎′
𝟐𝟎′′
𝟐
]
= 𝟓𝟐. 𝟑𝟑 𝐦
T1 = 100 – 27.112
= 72.888 m
T2 = 72.888 + 52.95
= 125.839 m

15. ANALYSIS DATA
The data that was analysed may be used since method 2
(circular curve utilising deflection angle for deflection
angle and cumulative has the same value) can be used.
DISCUSSION
The issue is that hot temperature causes eyesight to
become less focused.
Solved: do the practical task in a dim environment and
offer water to keep hydrated.
CONCLUSION
Because the calculation for the value of Data Offset From
Tangent Line and Circular Curve Using Deflection Angle is
the same, the conclusion that can be said is the outcome
of practical work may be accepted. JT = 27.112 m, L =
52.98 m, and C = 52.33 m