1. This document discusses various analog modulation techniques used to transmit digital data, including ASK, FSK, PSK, and QAM. 2. It provides examples and explanations of how each technique works, such as varying the amplitude (ASK), frequency (FSK), or phase (PSK) of a carrier signal to represent the 1s and 0s of digital data. 3. QAM is described as a technique that modulates signals onto both the cosine (in-phase) and sine (quadrature-phase) components of a carrier, allowing it to encode multiple bits per symbol.

1. 1
Analog TransmissionAnalog Transmission
of Digital Data:of Digital Data:
ASK, FSK, PSK, QAMASK, FSK, PSK, QAM
CSE 3213, Fall 2010
Instructor: N. Vlajic
Required reading:
Garcia 3.7

2. 2
Why Do We Need Digital-to-Analog Conversion?!
1) The medium/channel is band pass, and/or
2) Multiple users need to share the medium.

3. 3
Modulation of Digital Data
ModulationModulation – process of converting digital data or a low-pass
analog to band-pass (higher-frequency) analog signal
Digital-to-analog modulation.
Analog-to-analog modulation.
Carrier SignalCarrier Signal – aka carrier freq. or modulated signal - high freq.
signal that acts as a basis for the information signal
• information signal is called modulating signal
freq
bandpass channel

4. 4
Modulation of Digital Data (cont.)
DigitalDigital--toto--AnalogAnalog
ModulationModulation
– process of changing one of the characteristic
of an analog signal (typically a sinewave) based
on the information in a digital signal
• sinewave is defined by 3 characteristics (amplitude,
frequency, and phase) ⇒ digital data (binary 0 & 1)
can be represented by varying any of the three
• application: transmission of digital data over
telephone wire (modem)
Types of DigitalTypes of Digital--toto--AnalogAnalog
ModulationModulation

5. 5
Modulation of Digital Data: ASK
ASKASK – strength of carrier signal is varied to represent binary 1 or 0
• both frequency & phase remain constant while amplitude changes
• commonly, one of the amplitudes is zero
• demodulation: only the presence or absence of a sinusoid in a
given time interval needs to be determined
• advantage: simplicity
• disadvantage: ASK is very susceptible to noise interference –
noise usually (only) affects the amplitude, therefore ASK is the
modulation technique most affected by noise
• application: ASK is used to transmit digital data over optical fiber
⎩
⎨
⎧
=
⎩
⎨
⎧
=
1binaryt),fAcos(2
0binary0,
1binaryt),fcos(2A
0binaryt),fcos(2A
s(t)
cc1
c0
ππ
π
Is this picture,
from the textbook,
entirely correct?!
+A
-A

6. 6
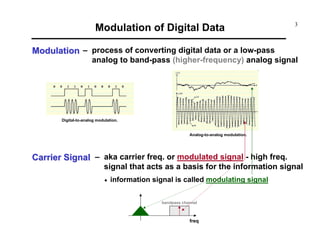
Modulation of Digital Data: ASK (cont.)
Example [ ASK ]
vd(t)
vc(t)
vASK(t)
How does the frequency spectrum of vASK(t) look like!?
fvd(f) vc(f)

7. 7
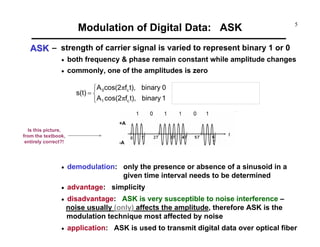
Modulation of Digital Data: ASK (cont.)
ASKASK--Modulated Signal: Frequency SpectrumModulated Signal: Frequency Spectrum
t)cos(ωt)fcos(2(t)v ccc == π
⎥
⎦
⎤
⎢
⎣
⎡
−+−+⋅= ...tcos5ω
5π
2
tcos3ω
3π
2
tcosω
π
2
2
1
A(t)v 000d
Carrier signal: , where 2πfc=ωc
Digital signal:
(unipolar!!!)
ωc ωωd_max
Modulated signal:
( ) ( )[ ]
( ) ( )[ ] ...t3ωωcost3ωωcos
3π
1
-tωωcostωωcos
π
1
tcosω
2
1
...tcos3ωtcosω
3π
2
-tcosωtcosω
π
2
tcosω
2
1
...tcos5ω
5π
2
tcos3ω
3π
2
tcosω
π
2
2
1
tcosω
(t)v(t)v(t)v
0c0c
0c0cc
0c0cc
000c
dcASK
+++−−
++−+=
=+⋅⋅+=
=⎥
⎦
⎤
⎢
⎣
⎡
−+−+⋅=
=⋅=
( )B)cos(AB)-cos(A
2
1
cosBcosA ++=⋅
ωc ωωc+ωd_maxωc-ωd_max

8. 8
Modulation of Digital Data: FSK
FSKFSK – frequency of carrier signal is varied to represent binary 1 or 0
• peak amplitude & phase remain constant during each bit interval
• demodulation: demodulator must be able to determine which of
two possible frequencies is present at a given time
• advantage: FSK is less susceptible to errors than ASK – receiver
looks for specific frequency changes over a number
of intervals, so voltage (noise) spikes can be ignored
• disadvantage: FSK spectrum is 2 x ASK spectrum
• application: over voice lines, in high-freq. radio transmission, etc.
⎩
⎨
⎧
=
1binaryt),fAcos(2
0binaryt),fAcos(2
s(t)
2
1
π
π
f1<f2
+A
-A

9. 9
Modulation of Digital Data: FSK (cont.)
Example [ FSK ]
vd(t)
vc1(t)
vc2(t)
vFSK(t)
ω1 ωωd_max ω2
ω1 ωω1-ωd_max
ω2 ω2+ωd_max

10. 10
Modulation of Digital Data: FSK (cont.)
FSKFSK--Modulated Signal: Frequency SpectrumModulated Signal: Frequency Spectrum
(t)vd
Digital signal: - modulated with ω1 , and
- modulated with ω2
Modulated signal:
( ) ( )[ ]
( ) ( )[ ]
( ) ( )[ ]
( ) ( )[ ] ++++−+
++−−
++++−−
++−+=
=
=⎥⎦
⎤
⎢⎣
⎡
−−+−⋅+
+⎥
⎦
⎤
⎢
⎣
⎡
−+−+⋅=
=−⋅+⋅=
...t3ωωcost3ωωcos
3π
1
-tωωcostωωcos
π
1
tcosω
2
1
...t3ωωcost3ωωcos
3π
1
-tωωcostωωcos
π
1
tcosω
2
1
...tcos5ω
5π
2
tcos3ω
3π
2
tcosω
π
2
2
1
tcosω
...tcos5ω
5π
2
tcos3ω
3π
2
tcosω
π
2
2
1
tcosω
(t))vtcosω(t)vtcosω(t)v
0202
02022
0101
01011
0002
0001
d2d1FSK
...
1(
(t)v1-(t)'v dd =

11. 11
PSKPSK – phase of carrier signal is varied to represent binary 1 or 0
• peak amplitude & freq. remain constant during each bit interval
• example: binary 1 = 0º phase, binary 0 = 180º (πrad) phase
⇒ PSK is equivalent to multiplying carrier signal by +1 when the
information is 1, and by -1 when the information is 0
• demodulation: demodulator must determine the phase of received
sinusoid with respect to some reference phase
• advantage: PSK is less susceptible to errors than ASK, while it
requires/occupies the same bandwidth as ASK
more efficient use of bandwidth (higher data-rate)
are possible, compared to FSK !!!
• disadvantage: more complex signal detection / recovery process,
than in ASK and FSK
⎩
⎨
⎧
+
=
0binary),tfAcos(2
1binaryt),fAcos(2
s(t)
c
c
ππ
π
Modulation of Digital Data: PSK
2-PSK, or
Binary PSK,
since only 2
different phases
are used.
+A
-A
⎩
⎨
⎧
=
0binaryt),fAcos(2-
1binaryt),fAcos(2
s(t)
c
c
π
π

12. 12
Modulation of Digital Data: PSK (cont.)
Example [ PSK ]
vd(t)
vc(t)
vPSK(t)
ωc ωωd_max ωc ωωc+ωd_maxωc-ωd_max

13. 13
Modulation of Digital Data: PSK (cont.)
PSK DetectionPSK Detection – multiply the received / modulated signal
by 2*cos(2πfct)
• resulting signal
• by removing the oscillatory part with a
low-pass filter, the original baseband signal
(i.e. the original binary sequence) can be
easily determined
[ ] 1binary,t)fcos(41At)f(22Acos cc
2
ππ +=
[ ] 0binary,t)fcos(41At)f(22Acos- cc
2
ππ +−=
t)fAcos(2 cπ±
( )2Acos1
2
1
Acos2
+=

14. 14
Modulation of Digital Data: PSK (cont.)
1 1 1 10 01 1 1 10 0Information
Baseband
Signal
+A
-A
0 T 2T 3T 4T 5T 6T
+A
-A
0 T 2T 3T 4T 5T 6T
+A
-A
0 T 2T 3T 4T 5T 6T
+A
-A
0 T 2T 3T 4T 5T 6T
Modulated
Signal
x(t)
A cos(2πft) -A cos(2πft)
After multiplication
at receiver
x(t) cos(2πfct)
+A
-A
0 T 2T 3T 4T 5T 6T
+A
-A
0 T 2T 3T 4T 5T 6T
A {1 + cos(4πft)} -A {1 + cos(4πft)}
Baseband
signal discernable
after smoothing
+A
-A
0 T 2T 3T 4T 5T 6T
sender
receiver
Signal shifted above / below zero level.

15. 15
Modulation of Digital Data: PSK (cont.)
B
fc+B
f
f
fc-B fc
• If bandpass channel has bandwidth Wc [Hz],
then baseband channel has Wc/2 [Hz] available, so
modulation system supports 2*(Wc/2) = Wc [pulses/second]
recall Nyqyist Law: baseband transmission system of bandwidth Wc [Hz]
can theoretically support 2 Wc pulses/sec
Facts from Modulation TheoryFacts from Modulation Theory
Wc
Wc/2
Baseband signal x(t) with
bandwidth Wc/2
If
then
Modulated signal
x(t)cos(2πfct) has
bandwidth Wc Hz
How can we recover the factor 2 in supported data-rate !?
Data rate = 2*Wc/2 = B [bps]

16. 16
Modulation of Digital Data: PSK (cont.)
QPSK = 4QPSK = 4--PSKPSK – PSK that uses phase shifts of 90º=π/2 rad ⇒ 4
different signals generated, each representing 2 bits
• advantage: higher data rate than in PSK (2 bits per bit
interval), while bandwidth occupancy remains the same
• 4-PSK can easily be extended to 8-PSK, i.e. n-PSK
• however, higher rate PSK schemes are limited by the
ability of equipment to distinguish small differences in
phase
⎪
⎪
⎪
⎩
⎪
⎪
⎪
⎨
⎧
+
+
+
=
11binary),
2
3
tfAcos(2
10binary),tfAcos(2
01binary),
2
tfAcos(2
00binaryt),fAcos(2
s(t)
c
c
c
c
π
π
ππ
π
π
π

17. 17
Modulation of Digital Data: QAM
QuadratureQuadrature
AmplitudeAmplitude
ModulationModulation
(QAM)(QAM)
– uses “two-dimensional” signalling
• original information stream is split into two sequences that
consist of odd and even symbols, e.g. Bk and Ak
• Ak sequence (in-phase comp.) is modulated by
Bk sequence (quadrature-phase comp.) is modulated by
• composite signal is sent
through the channel
• advantage: data rate = 2 bits per bit-interval!
B1 B2 B3A1 A2 A3 …
Ak x
cos(2πfct)
Yi(t) = Ak cos(2πfct)
Bk
x
sin(2πfct)
Yq(t) = Bk sin(2πfct)
+
Transmitted
Signal
Y(t) = Ak cos(2πfct) + Bk sin(2πfct)
t)fcos(2 cπ
t)fsin(2 cπ
t)fsin(2Bt)fcos(2A ckck ππ +
1 -1 1 1 -1 1 …
1 0 1 1 0 1 …

18. 18
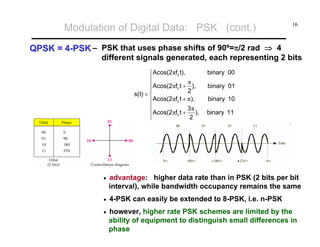
Modulation of Digital Data: QAM (cont.)
Example [ QAM ]
Bk
vd(t)
Ak
sin(ωct)
cos(ωct)

19. 19
Modulation of Digital Data: QAM
QAMQAM DemodulationDemodulation • by multiplying Y(t) by and then low-
pass filtering the resultant signal, sequence Ak is
obtained
t)fcos(22 cπ⋅
• by multiplying Y(t) by and then low-
pass filtering the resultant signal, sequence Bk is
obtained
t)fsin(22 cπ⋅
=+ t)fsin(2Bt)fcos(2A ckck ππ
( )cos(2A)1
2
1
(A)cos2
+=
( )cos(2A)1
2
1
(A)sin2
−=
(A)2sin(A)cossin(2A) =
Y(t) x
2cos(2πfct)
2Akcos2(2πfct)+2Bk cos(2πfct)sin(2πfct)
= Ak {1 + cos(4πfct)}+Bk {0 + sin(4πfct)}
Lowpass
filter
(smoother)
Ak
2Bk sin2(2πfct)+2Ak cos(2πfct)sin(2πfct)
= Bk {1 - cos(4πfct)}+Ak {0 + sin(4πfct)}
x
2sin(2πfct)
Bk
Lowpass
filter
(smoother)
smoothed to zero
smoothed to zero
Y(t) x
2cos(2πfct)
2Akcos2(2πfct)+2Bk cos(2πfct)sin(2πfct)
= Ak {1 + cos(4πfct)}+Bk {0 + sin(4πfct)}
Lowpass
filter
(smoother)
Ak
x
2cos(2πfct)
2Akcos2(2πfct)+2Bk cos(2πfct)sin(2πfct)
= Ak {1 + cos(4πfct)}+Bk {0 + sin(4πfct)}
Lowpass
filter
(smoother)
Ak
2Bk sin2(2πfct)+2Ak cos(2πfct)sin(2πfct)
= Bk {1 - cos(4πfct)}+Ak {0 + sin(4πfct)}
x
2sin(2πfct)
Bk
Lowpass
filter
(smoother)
x
2sin(2πfct)
Bk
Lowpass
filter
(smoother)
smoothed to zero
smoothed to zero

20. 20
Signal Constellation
Constellation DiagramConstellation Diagram – used to represents possible symbols that may
be selected by a given modulation scheme as
points in 2-D plane
• X-axis is related to in-phase carrier: cos(ωct)
the projection of the point on the X-axis defines
the peak amplitude of the in-phase component
• Y-axis is related to quadrature carrier: sin(ωct)
the projection of the point on the Y-axis defines
the peak amplitude of the quadrature component
• the length of line that connects the point to
the origin is the peak amplitude of the signal
element (combination of X & Y components)
• the angle the line makes with the X-axis is the
phase of the signal element

21. 21
Modulation of Digital Data: QAM
QAM cont.QAM cont. – QAM can also be seen as a combination of ASK & PSK
( ) )
A
B
tantfcos(2BAt)fsin(2Bt)fcos(2AY(t)
k
k1-
ckkckck ++=+= πππ 2
1
22
Ak
Bk
(A, A)
(A,-A)(-A,-A)
(-A,A)
Ak
Bk
Ak
Bk
(A, A)
(A,-A)(-A,-A)
(-A,A)
4-level QAM

22. 22
Ak
Bk
Ak
Bk
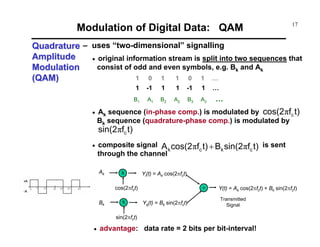
Modulation of Digital Data: QAM
1616--level QAMlevel QAM – the number of bits transmitted per T [sec] interval
can be further increased by increasing the number
of levels used
• in case of 16-level QAM, Ak and Bk individually can
assume 4 different levels: -1, -1/3, 1/3, 1
• data rate: 4 bits/pulse ⇒ 4W bits/second
( ) )
A
B
tantfcos(2BAt)fsin(2Bt)fcos(2AY(t)
k
k1-
ckkckck ++=+= πππ 2
1
22
In QAM various combinations of amplitude and phase are employed
to achieve higher digital data rates.
Amplitude changes are susceptible to noise ⇒ the number of phase shifts used
by a QAM system is always greater than the number of amplitude shifts.
Ak and Bk individually
can take on 4 different values;
the resultant signal can take
on (only) 3 different values!!!