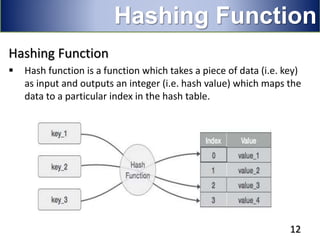
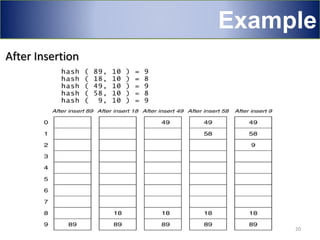
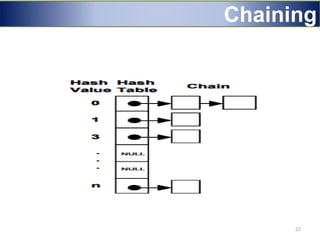
Hashing is a technique used to map data of arbitrary size to data of fixed size. It works by using a hash function to compute an index into an array/table from the search key. This allows for very fast average case performance of O(1) time for operations like insertion, deletion and searching. However, collisions can occur when two keys map to the same index, degrading performance. Common techniques to handle collisions include linear probing, quadratic probing and chaining via linked lists. Hashing is widely used to implement symbol tables in compilers and data structures like sets and maps.

1. 1

2. Presented By
UMAIR
KHAN
HASHING TABLES
2

3. Table of Content
 Introduction.
 Searching Methods.
 What is Hashing .
 Simple Hashing .
 Collision in Hashing.
 Techniques for Overcome Collisions.
 Advantages And Disadvantages.
 Summary .
 Q /A Session
3

4. Introduction
 Process of finding an element within the
list of elements in order or randomly.
 Searching Takes About 20% to 25% of computer
Execution Time.
 So That why we need to increase the efficiency of
our Searching function
4

5. LINEAR SEARCHING
BINARY SEARCH
HASH TABLES
5
Searching

6. Linear Searching
 Finding a value in a list of values.
 Searching is the process of locating given value
position in a list of values.
 Time complexity of Linear Search is O(n)
where n is total number of elements in the list.
6
Linear Searching

7. Linear Search
Find(12); //Searching Function
7
Example
14 33 12 55 2 30 41
Found
88

8. Binary Searching
 Finding a value in a list of values.
 Searching is the process of locating given value
position in a list of values.
 Time complexity of Linear Search is O(log n)
where n is total number of elements in the list.
 The binary search algorithm can be used with
only sorted list of element.
 Mid=(low+end)/2;
 Above formula is for finding the middle of list .
8
Binary Searching

9. Binary Search
Find(12); //Searching Function
9
Example
14 33 12 55 2 30 4188
Start End

10. Function Find(int x)
{
While(start<=end)
{
Int mid=(start+end)/2;
If(x==A[mid]
{
cout<<X<<“ Value Successfully found In Given Array”<<endl;
Break;
}
Else if(x>A[mid])
{
Start=mid+1;
}
Else
End=mid-1;
}
If(x==-1)
{
Cout<<“Element not Found in Array”<<endl;
}
10
Example

11. Hashing
 Hashing is the process of indexing and retrieving element (data)
to provide faster way of finding the element using the hash key.
 Hash table is just an array which maps a key (data) into the data
structure with the help of hash function.
 Insertion ,Deletion can be Performed by using hash Function .
 The Time Complexity of Hashing Is O(1).
 Hash key is a value which provides the index value where the
actual data is likely to store in the data structure.
 All the data values are inserted into the hash table based on the
hash key value
 Hashing is another approach in which time required to search an
element doesn't depend on the number of element
11
Hashing

12. Hashing Function
 Hash function is a function which takes a piece of data (i.e. key)
as input and outputs an integer (i.e. hash value) which maps the
data to a particular index in the hash table.
12
Hashing Function

13. Hashing Function
 To achieve a good hashing mechanism, It is
important to have a good hash function.
 Occurs Less collisions.
 Uniform distribution
 Hash Function
Hash(key) //hash function
{
return key%size;
}
13
Hashing Function

14. Insertion in Hash Tables
 Now Here We Insert some values into hash
Table using hash function.
Hash(20); //Here We Pass 20 As key and Size of
Array is 20
Hash will return the index 2
Insert(2,45); //insertion function 2 is index and
45 is value
0 1 2 3 4 5
14
Insertion in Hash Table
45

15. Searching in Hash Table
 Searching is also related to insertion .
 For searching you just enter key and hash
function will convert the key into relative
index number.
 Use Linear Probing to get the element ahead
if the element is not found at the Computed
hash code.
 This will take Constant Time O(1).
 The Wrest case will be O(n).
15
Searching in Hash Table

16. Hash(37); //will Return the key 17
Hash(17); //will Return the Key 17
 Now Here The Hash Function will return same
index for two different keys .
 This case is called in Hash Table called Collision.
 When two keys are mapped to the same
position called collision.
 To overcome Collision We apply some
techniques
16
Collision in Hashing

17. Linear Probing
 Linear search in the array from the
position where collision occurred.
Chaining
 Uses a Linked List at each position in the
Hash Table.
17
Collision Resolution

18.  Open addressing / probing is carried out for insertion
into fixed size hash tables.
 If the index given by the hash function is occupied, then
increment the table position by some number.
 It may be an empty location in Table.
 Start Search for Empty Slot in table than stop search
and insert into them.
 Quadratic Probing
 increment the position computed by the hash function.
 Double Hash:
 compute the index as a function of two different hash
functions.
18
Linear Probing

19. Insertion
 Insert items with keys: 89, 18, 49, 58, 9 into an
empty hash table.
 Table size is 10.
 Hash function is hash(x) = x mod 10.
Linear Probing

20. 20
Example
After Insertion

21. Chaining Resolution
 Uses a Linked List at each position in the Hash
Table.
 An array is used to hold the key and a pointer
to a liked list.
 Uses more space.
 More complex to implement.
 A linked list at every element in the array
21
Chaining Resolution

22. 22
Chaining

23. Hashing Applications
 Compilers use hash tables to implement the
symbol table (a data structure to keep track of
declared variables).
 Game programs use hash tables to keep track
of positions it has encountered .
 Online spelling checkers.
23

24.  Hash tables can be used to implement the
insert and find operations in constant average
time.
 it depends on the load factor not on the number of
items in the table
24
Summary

25. 25
Any Question

26. “Learn The Rules Like Pro So
You Can Break them Like
Artist”
26

27. Thank You
27