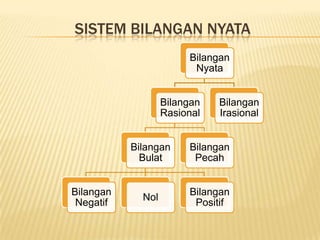
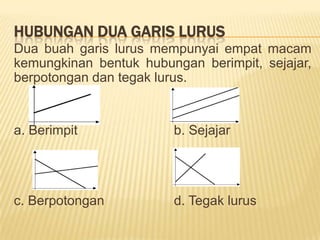
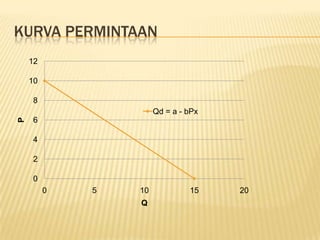
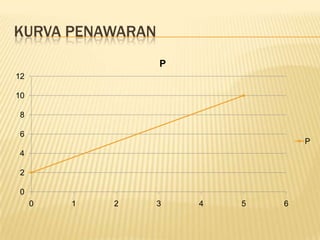
Dokumen ini membahas matematika ekonomi dan bisnis, mencakup pengertian, model ekonomi, fungsi matematis, serta sistem persamaan linier yang digunakan dalam analisis ekonomi. Ada juga penjelasan tentang variabel, konstanta, koefisien, serta berbagai metode untuk menyelesaikan sistem persamaan linier. Selain itu, dokumen ini menjelaskan operasi himpunan dalam konteks ekonomi dan bisnis.

1. MATEMATIKA EKONOMI & BISNISOlehA. Gustang

2. Sumber / refrensi- MatematikaEkonomi & BisniaJosepBintangKalangiPenerbitSalembaEmpatMatematikaBisnisRudy Badruddin, AlgifariPenerbit BPFE Yogyakarta

3. MATERI PERKULIAHAN 1. PendahuluanSifat-SifatMatemaikaEkonomidanBisnis2. KonsepDasarMatematikadanEkonomiBisnis Model Ekonomi3. Macam-macamFungsidalamEkonomidanBisnisFungsi Linear Fungsi Non LinearFungsiEksponen4. MatematikaKeuangan

4. pendahuluanMatematika = suatucabanglogika dg kerangkasistematisutkmempelajarihubungankuantitatifantarpeubah (variabel)

5. Bedakan: MatematikaMurni & Terapan

6. MatematikaMurni: lambang2 ygdigunakanmenyatakankonsepabstrakygnilainyasesuaidefinisinya (mis. - 5 < X < 12)

7. MatematikaTerapan: lambang2 ygdipakaimenyatakanpeubah (variabel) ygnilainyasesuaipengamatandidunianyata; mis. P = variabelharga, maka P  0MatematikaekonomidanbisnisMatematikaEkonomidanBisnis= matematikaterapanIlmuekonomifokuskekonsepkuantitatif, menyangkutvariabelsepertibiaya, harga, upah, permintaan-penawaran, penerimaan-biaya-laba, makabanyakanalisisekonomimenggunakananalisismatematikaterapanHubungankuantitatifantarvariabelekonomidipelajarisecaraempiris=>model matematisContoh :Konsumsi dg PendapatanPermintaan (demand) dg Harga

8. Model ekonomiModel Ekonomi= Penyederhanaanhubunganantaravariabel-variabelekonomi.Model Ekonomidapatberbentuk model matematikadan non-matematika. Apabilaberbentuk model matematika, makaakanterdiriatassatuatausekumpulanpersamaan. Persamaanterdiriatassejumlahvariabel, konstanta, koefisien, dan/atau parameter.

9. VARIABEL, KONSTANTA, KOEFISIEN, DAN PARAMETERVariabeladalahsesuatu yang nilainyadapatberubah-ubahdalamsuatumasalahtertentu.Misalnya;Harga (Price) = P; Jumlahygdiminta/ditawarkan (Quantity) = Q; Biaya (Cost) = C; Penerimaan (Revenue) = R; Investasi (Investment) = I; Tingkat Bunga (Interest Rate) = I dll.Variabelterdiridari;Variabel Endogen = suatuvariabelygnilaipenyelesaiannyadiperolehdaridalam model;VariabelEksogen= suatuvariabel yang nilai-nilainyadiperolehdariluar model, atausudahditentukanberdasarkan data yang ada.

10. Konstantaadalahsuatubilangannyatatunggal yang nilainyatidakberubah-ubahdalamsuatumasalahtertentu.Koefisienadalahangkapengalikonstanterhadapvarabelnya. (Misal 5R; 4P; atau 0.3C)Parameter adalahsuatunilaitertentudalamsuatumasalahtertentudanmungkinakanmenjadinilai yang lain padasuatumasalah yang lainnya. (Biasanyadilambangkan dg hurufawalabjadyunaniatau Arab, Misalnyaα, β, danҲatau a, b dan c.

11. PersamaandanpertidaksamaanPersamaanadalahpernyataanbahwadualambangadalahsama. disimbolkandengantanda = (baca “samadengan”), sedangkanPertidaksamaanadalahsuatupernyataan yang menyatakanbahwadualambangadalahtidaksama. Disimbolkandengantanda < (baca “lebihkecil”) atau > (baca: “lebihbesar)

12. PersamaandalamMatematikaEkonomidanBisnisterdiridariTigaMacam, yaitu:PersamaanDefinisi (Identity, =) adalahsuatubentukkesamaandiantaraduapernyataan yang mempunyaiarti yang sama.PersamaanPerilaku (behaioral equation) adalahsuatupersamaanygmenunjukkanbahwaperubahanperilakusuatuvariabelsebagaiakibatdariperubahanvariabellainnyaygadahubungannya.KondisiKeseimbanganadalahsuatupersamaanygmenggambarkanpersyaratanuntukpencapaiankeseimbangan (equilibrium). Misalnya; Qd = Qs ; S = I

13. Sistembilangannyata

14. BilanganRasionaladalahbilangan yang angkadesimalnyaberakhirdengannolatauberulang. (misalnya; 5/1 = 5,00; 1/3 = 0,333BilanganIrasionaladalahbilangan yang angkadesimalnyatidakberakhirdengannolatautidakberulang. (misalnya; √2 = 1,41423… )

15. KonsepdanteorihimpunanKonsepHimpunanadalahsuatukonsepyg paling mendasarbagiilmumatematika modern padaumumnyadandibidangilmuekonomidanbisnispadakhususnya. Karenadalambidangekonomidanbisnisterutamadalamhalpembentukan model kitaharusmenggunakansehimpunan/sekelompok data observasidarilapangan.

16. DefinisidanpenulisanhimpunanHimpunanadalahkelompokdariobjek-objek yang berbeda.Objek-objekdalamhimpunandisebutelemenhimpunan.Penulisanhimpunanada 2 cara, yaitu;1. Denganmendaftarkansatu per satu. Misal; S adalahhimpunandaribilanganbulatpositifdari 1 sampai 5, dapatditulismenjadi. S = {1,2,3,4,5}.2. Dengancaradeskriptif. Misal; B adalahsuatuhimpunandarisemuabilanganbulatypositif, dapatditulismenjadi; B = {x|xbilanganbulatpositif}

17. Operasi HimpunanGabungan (Union) notasi UIrisan(Intersection) notasi∩Selisihnotasi (-)HimpunanBagian (subset) notasiсPelengkap(complement) misal Him. AC

18. a  A berarti a anggota him A a  A berarti a bukananggota him Anotasiuntukhimpunankosong  atau { }Beberapa notasi Himpunan

19. Kaidah matematika dlm HimpunanIdempoten A  A = A AU A = AAsosiatif (A  B)  C = A  (B  C)Komutatif A  B = B  ADistributif AU(B  C) = (AUB)  (AUC)

20. IdentitasA U = A A U S = SKelengkapanA U Ac = S(Ac)c = ADe Morgan(AUB)c = Ac Bc

21. FUNGSIPenerapanfungsidalamekonomidanbisnismerupakansalahsatubagian yang sangatpentinguntukdipelajari, karena model-model ekonomi yang berbentukmatematikabiasanyadinyatakandenganfungsi. Fungsidalammatematikamenyatakansuatuhubungan formal diantaraduahimpunan data. Jikahimpunan data tersebutadalahvariabel, makafungsidapatdikatakansebagaihubunganantaraduavariabel.

22. Fungsiadalahsuatubentukhubunganmatematis yang menyatakanhubunganketergantungan (hubungan fungsional) antara satu variabel dengan variabel lain. Sebuahfungsidibentukolehbeberapaunsuryaitu: variabel, koefisien, dankonstanta. Variabeldankoefisiensenantiasaterdapatdalamsetiapfungsi.Variabeladalahunsurpembentukfungsi yang mencerminkanataumewakilifaktor (data) tertentu, dilambangkandenganhuruf-huruflatin. Berdasarkankedudukanatausifatnya, didalamsetiapfungsiterdapatduamacamvariabelyaituvariabelbebas(independent variable) danvariabelterikat (dependent variable). Variabelbebasadalahvariabel yang nilainyatidaktergantungpadavariabel lain, sedangkanvariabelterikatadalahvariabel yang nilainyatergantungpadavariabel lain.

23. Koefisien adalah bilangan atau angka yang terkait pada dan terletak di depan suatu variabeldalamsebuahfungsi.Konstantaadalahbilanganatauangka yang (kadang-kadang) turutmembentuksebuahfungsitetapiberdirisendirisebagaibilangan (tidakterkaitpadasuatuvariabeltertentu). y = 5 + 0,8x y : variabelterikat x : variabelbebas 0,8 : koefisienvariabel x 5 : konstantaSedangkannotasisebuahfungsisecaraumumadalah: y = f(x)

24. FUNGSI LINIERFungsi linieradalahfungsi yang paling sederhanakarenahanyamempunyaisatuvariabelbebasdanberpangkatsatupadavariabelbebastersebut, sehinggaseringdisebutsebagaifungsiberderajadsatu. Bentukumumpersamaan linier adalah: y = a + bx; dimana a adalahkonstantadan b adalahkoefisien (b≠0). Atauseringdinyatakandalambentukimplisitberikut: Ax + By + C = 0

25. A. KEMIRINGAN DAN PENGGAL GARISSesuaidengannamanyafungsi linier jikadigambarkanpadakoordinatcartesiusakanberbentukgarislurus (linier). Kemiringanpadasetiaptitik yang terletakpadagarislurustersebutadalahsama. Hal iniditunjukkanolehkoefisien b padapersamaany = a + bx. Koefisieniniuntukmengukurperubahannilaivariabelterikaty sebagaiakibatdariperubahanvariabelbebasx sebesarsatu unit. Sedangkan a adalahpenggalgarispadasumbuvertikal(sumbuy). Penggal a mencerminkannilai y pada kedudukan x = 0. Kemiringan (slope)darifungsi linier adalahsamadenganperubahanvariabelterikat x dibagidenganperubahandalamvariabelbebasy. Kemiringanjugadisebutgradien yang dilambangkandenganhuruf m. Jadi:Kemiringan = m =

26. Sebagaicontoh, y = 15 – 2x, kemiringannyaadalah –2. Iniberartibahwauntuksetiapkenaikkan satu unit variabel x akan menurunkan 2 unit variabel y.

27. MENENTUKAN PERSAMAAN GARISSebuahpersamaan linier dapatdibentukmelaluibeberapamacamcara, antara lain: (1) metode dua titik dan (2) metode satu titik dan satu kemiringan.1. MetodeDuaTitikApabiladiketahuiduatitik A dan B dengankoordinatmasing-masing (x1, y1) dan (x2, y2), maka rumus persamaan liniernya adalah:

28. misaldiketahuititik A (2,3) dantitik B (6,5), makapersamaanliniernyaadalah:4y – 12 = 2x – 44y = 2x + 8Y = 0,5x + 2

29. 2. Metode Satu Titik dan Satu Kemiringan Dari sebuahtitik A (x1, y1) dansuatukemiringan (m)dapatdibentuksebuahpersamaan linier denganrumussebagaiberikut; y – y1 = m (x – x1)Misaldiketahuititik A (2,3) dankemiringanm=0,5 makapersamaanliniernyaadalah: y – y1 = m (x – x1)y – 3 = 0,5(x – 2)Y – 3 = 0,5x – 1Y = 0,5x + 2

30. HUBUNGAN DUA GARIS LURUSDuabuahgarislurusmempunyaiempatmacamkemungkinanbentukhubunganberimpit, sejajar, berpotongandantegaklurus.a. Berimpit b. Sejajarc. Berpotongan d. Tegaklurus

31. Berimpit, dua buah garis akan berimpit apabila persamaan garis yang satu merupakan kelipatan dari (proporsionalterhadap) persamaan garis yang lain.Sejajar, duabuahgarisakansejajarapabilakemiringangaris yang satusamadengankemiringangaris yang lain (m1 = m2).Berpotongan, duabuahgarisakanberpotonganapabilakemiringangaris yang satutidaksamadengankemiringangaris yang lain (m1 ?m2).Tegak lurus, dua garis akan saling tegak lurus apabila kemiringan garis yang satu merupakan kebalikandarikemiringangaris yang lain dengantanda yang berlawanan (m1 = - 1/m2).Atau nilai perkalian kemiringannya menghasilkan –1 (m1 x m2 = -1).

32. Latihan:1. Carilahkemiringandantitikpotongsumbu y padapersamaangarisberikutini:a. 3x – 2y + 12 = 0b. 2x – 5y – 10 = 0c. 4x – 6y = 102. Untuksetiappasangantitik-titikkoordinatberikutcarilahpersamaangarislurusnya:a. (3,5) dan (10,2)b. (-6,-4) dan (10,8)3. Untuk setiap pasangan titik koordinat dan kemiringan (m) berikut ini tentukan persamaan garislurusnya:a. (2,6), m = 0,4b. (5,8), m = -1,64. Tentukanhimpunanpenyelesaiandarisistempersamaan linier berikutdenganmetodeeliminasi:a. 2x – 3y = 5 dan 3x – 2y = -4b. 4x + 3y = 16 dan x – 2y = 45. Tentukanhimpunanpenyelesaiandarisistempersamaan linier berikutdenganmetodesubstitusi:a. x – y = 2 dan 2x + 3y = 9b. x – y = -1 dan 3x + 2y = 126. Tentukanhimpunanpenyelesaiandarisistempersamaan linier berikutdenganmetodedeterminan:a. x + y = 5 dan 2x + 3y = 12b. 2x – 3y = 13 dan 4x + y = 15

33. SISTEM PERSAMAAN LINIERPenyelesaiansuatusistempersamaan linier adalahsuatuhimpunannilaiyang memenuhi secara serentak (simultan) semua persamaan-persamaan dari sistem tersebut. Atausecarasederhanapenyelesaiansistempersamaan linier adalahmenentukantitikpotongdariduapersamaan linier. Adatigacara yang dapatdigunakanuntukpenyelesaiansuatusistempersamaan linier, yaitu: (1). MetodeSubstitusi, (2). MetodeEliminasi, dan(3). MetodeDeterminan.

34. MetodeSubstitusiMisal: carilahnilaivariabelx dan y dariduapersamaanberikut: 2x+3y=21 danx+4y=23 ?Jawab:Salahsatupersamaandirubahdahulumenjadi y = ... atau x = .... Misalpersamaan x+4y=23 dirubahmenjadi x=23-4y. Kemudiandisubstitusikankedalampersamaan yang satu.x = 23-4y Þ 2x + 3y = 212(23-4y) + 3y = 2146 – 8y + 3y = 2146 – 5y = 2125 = 5yy = 5Untukmendapatkannilai x, substitusikan y = 5 kedalamsalahsatupersamaan.y = 5 Þ 2x + 3y = 212x + 3(5) = 212x + 15 = 212x = 21 – 15x = 6/2x = 3Jadihimpunanpenyelesaian yang memenuhikeduapersamaantersebutadalahhimpunanpasangan (3,5)

35. MetodeEliminasiMisal: carilahnilaivariabelx dan y dariduapersamaanberikut: 3x-2y=7 dan2x+4y=10 ?Jawab:Misalvariabel yang hendakdieliminasiadalah y 3x - 2y = 7 |x 2| 6x – 4y = 14 2x + 4y = 10 |x 1| 2x + 4y = 10 + 8x + 0 = 24 x = 3Untukmendapatkannilai y, substitusikan x = 3 kedalamsalahsatupersamaan. x = 3 Þ 3(3) - 2y = 7 -2y = 7 – 9 2y = 2 y = 1Jadihimpunanpenyelesaian yang memenuhikeduapersamaantersebutadalahhimpunanpasangan (3,1)

36. MetodeDeterminanax + by = cdx + ey = fNilaix adalah: x =Nilai y adalah; y =Misal persamaan pada soalsebelumnyayaitu 3x-2y=7 dan 2x+4y=10 akandiselesaikandengancaradeterminan:

37. Nilaix adalah: x =Nilai y adalah; y =Jadihimpunanpenyelesaian yang memenuhikeduapersamaantersebutadalahhimpunanpasangan (3,1)

38. PENERAPAN FUNGSI LINIERFungsi linieradalahsuatufungsi yang sangatseringdigunakanolehparaahlielonomidanbisnisdalammenganalisadanmemecahkanmasalah-masalahekonomi. Hal inidikarenakanbahwakebanyakanmasalahekonomidanbisnisdapatdisederhanakanatauditerjemahkankedalam model yang berbentuk linier.Beberapapenerapanfungsi linier dalambidangekonomidanbisnisadalah:Fungsipermintaan, fungsipenawarandankeseimbanganpasarKeseimbangan Pasar Dua Macam ProdukPengaruhPajakdanSubsidiTerhadapKeseimbanganPasar.Fungsibiaya, fungsipendapatandananalisisPulangPokok(BEP=Break Even Point)Fungsi Konsumsi dan TabunganModelPenentuanPendapatanNasional

39. FUNGSI PERMINTAAN, FUNGSI PENAWARAN DAN KESEIMBANGAN PASARFUNGSI PERMINTAANFungsipermintaanmenunjukkanhubunganantarajumlahproduk yang dimintaolehkonsumendenganhargaproduk. Di dalamteoriekonomidijelaskanbahwajikaharganaikmakajumlahbarang yang dimintaturun, demikianjugasebaliknyabahwajikahargaturunmakajumlahbarang yang dimintanaik, sehinggagrafikfungsipermintaanmempunyaislope negatif (miring kekiri)Notasifungsipermintaanakanbarangx adalah:Qx = f (Px)Qx = a – b PxAtauPx =a/b – 1/b Qxdimana: Qx = Jumlahproduk x yang dimintaPx = Hargaproduk x a dan b = parameter

40. Kurvapermintaan

41. FUNGSI PENAWARANFungsipenawaranmenunjukkanhubunganantarajumlahproduk yang ditawarkanolehprodusenuntukdijualdenganhargaproduk. Di dalamteoriekonomidijelaskanbahwajikaharganaikmakajumlahbarang yang ditawarkanbertambah, demikianjugasebaliknyabahwajikahargaturunmakajumlahbarang yang ditawarkanturun, sehinggagrafikfungsipermintaanmempunyaislope positif (miring kekanan)Notasi fungsi penawaran akan barang x adalah:Qx = f (Px)Qx = -a + b PxAtauPx = a/b + 1/b Qxdimana: Qx = Jumlahproduk x yang ditawarkanPx = Hargaproduk x a dan b = parameterContoh: Fungsi pernawaran P = 3 + 0,5Q

42. Kurvapenawaran

43. KESEIMBANGAN PASARPasarsuatumacambarangdikatakanberadadalamkeseimbangan (equilibrium) apabilajumlahbarang yang dimintadipasartersebutsamadenganjumlahbarang yang ditawarkan. Secaramatematikdangrafikditunjukanolehkesamaan:Qd = QsatauPd = Psyaitu perpotongan kurva permintaan dengan kurva penawaran.

44. Kurvakeseimbanganpasar

45. B. KESEIMBANGAN PASAR DUA MACAM PRODUKDi pasarterkadangpermintaansuatubarangdipengaruhiolehpermintaanbarang. Inibisaterjadipadaduamacamprodukataulebih yang berhubungansecarasubstitusi (produkpengganti) atausecarakomplementer (produkpelengkap). Produksubstitusimisalnya: berasdengangandum, minyaktanahdengan gas elpiji, dan lain-lain. Sedangkanprodukkomplementermisalnya: tehdengangula, semen denganpasir, dan lain sebagainya. Dalampembahasan ini dibatasi interaksi dua macam produk saja. Secaramatematisfungsipermintaandanfungsipenawaranproduk yang beinteraksimempunyaiduavariabelbebas. Keduavariabelbebas yang mempengaruhijumlahjumlah yang dimintadanjumlah yang ditawarkanadalah (1) hargaprodukitusendiri, dan (2) hargaproduk lain yang salingberhubungan.

46. Notasifungsipermintaanmenjadi:Qdx = ao – a1Px + a2PyQdy = bo + b1Px - b2PySedangkanfungsipenawarannya:Qsx = -mo + m1Px + m2PyQsy = -no + n1Px + n2Py

47. Dimana: Qdx = Jumlah yang diminta dari produk XQdy = Jumlah yang dimintadariproduk YQsx = Jumlah yang ditawarkandariproduk XQsy = Jumlah yang ditawarkandariproduk YPx = Hargaproduk XPy = Hargaproduk Ya0, b0, m0, dan n0 adalah konstanta.Syaratkeseimbanganpasardicapaijika:Qsx = QdxdanQsy = Qdy

48. Contoh:Diketahuifungsipermintaandanfungsipenawarandariduamacamproduk yang mempunyaihubungansubstitusisebagaiberikut:Qdx = 5- 2Px + PyQdy = 6 + Px - PyDanQsx = -5 + 4Px - PyQsy = -4 - Px + 3PyCarilahhargadanjumlahkeseimbanganpasar !

49. PENGARUH PAJAK DAN SUBSIDI PADA KESEIMBANGAN PASARAdanyapajak yang dikenakanpemerintahataspenjualansuatubarangakanmenyebabkanprodusenmenaikkanhargajualbarangtersebutsebesartarifpajak per unit (t), sehinggafungsipenawarannyaakanberubah yang padaakhirnyakeseimbanganpasarakanberubah pula. Fungsipenawaransetelahpajakmenjadi:Ps = f(Q) + t atauQs = f(P - t)

50. Contoh:Fungsipermintaansuatuprodukditunjukkanoleh P=15-Q danfungsipenawaran P=0,5Q+3.TerhadapprodukinipemerintahmengenakanpajaksebesarRp 3 per unir.Berapahargadanjumlahkeseimbanganpasarsebelumdansesudahkenapajak ?Berapabesarpajak per unit yang ditanggungolehkonsumen ?Berapabesarpajak per unit yang ditanggungolehprodusen ?Berapa besar penerimaan pajak total oleh pemerintah ?

51. subsidiAdanyasubsidi yang diberikanpemerintahataspenjualansuatubarangakanmenyebabkanprodusenmenurunkanhargajualbarangtersebutsebesarsubsidi per unit (s), sehinggafungsipenawarannyaakanberubah yang padaakhirnyakeseimbanganpasarakanberubah pula.Fungsipenawaransetelahsubsidimenjadi:Ps = f(Q) - s atauQs = f(P + s)

52. AnalisispulangpokokPulangPokok (Break Even); Apabilapenerimaan total darihasilpenjualanproduksamadenganbiaya total yang dikeluarkanperusahaan.TR = TCTR = P.Q danTC = FC + VQDimana;

53. FUNGSI KONSUMSI DAN TABUNGANFungsiKonsumsi; C = a + bYdDimana; C = KonsumsiYd = PendapatanYgdapatdibelanjakana = Konsumsidasartertentuygtidaktergantungpadapendapatanb = Kecenderungankonsumsi marginal (MPC)Fungsi Tabungan;S = -a + (1-b)YdDimana; S = Tabungana = PendapatanYgdapatdibelanjakanYd = PendapatanYgdapatdibelanjakan(1-b) = Kecenderungankonsumsi marginal (MPC)

54. Fungsi non linearFungsiKuadratY = f(X) = aX2 + bX + cDimana; Y = VariabelTerikatX = VariabelBebasa, b, dan c = konstanta, dan a ≠ 0Koordinattitikpuncakdarisuatu parabola dapatdiperolehdenganrumus;

55. Rumuskuadrat

56. MACAM-MACAM PARABOLAJika a > 0 dan D > 0, maka parabola akanterbukakeatasdanmemotongsumbu X diduatitikygberlainan.Jika a > 0 dan D = 0, maka parabola akanterbukakeatasdanmenyinggungsumbu X diduatitikygberimpit.Jika a > 0 dan D < 0, maka parabola akanterbukakeatasdantidakmemotongmaupunmenyinggungsumbu X.Jika a < 0 dan D > 0, maka parabola akanterbukakebawahdanmemotongsumbu X diduatitikygberlainan.Jika a < 0 dan D = 0, maka parabola akanterbukakebawahdanmenyinggungsumbu X diduatitikygberimpit.Jika a < 0 dan D < 0, maka parabola akanterbukakebawahdantidakmemotongmaupunmenyinggungsumbu X.

57. Bentuk lain fungsikuadratX = f(Y) = aY2 + bY + cKurvanya Parabola HorizontalKoordinattitikpuncak Parabola adalah;

58. 2. Fungsipangkattiga (f. kubik)Y = a0 + a1X + a2X2 + a3X3Dimana a3 ≠ 0

59. 3. FungsirasionalBentukUmum;