Zat padat parno

FISIKA ZAT PADAT

Oleh
DRS. P A R N O, M.Si

DEPARTEMEN PENDIDIKAN NASIONAL
UNIVERSITAS NEGERI MALANG
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM

JURUSAN FISIKA
Pebruari 2006

Ralat fisika zat padat 2006

hal ralat
10 Gambar 1.9 CsCl
13 c/a = (2/3) akar 6
18 Baris ke-8 dalam table: ………. berikutnya
25 Pers (1.30) fkr,hkl
27 KBR seharusnya adalah KBr
35 interaksi seharusnya Interaksi
41 Baris ke-2 dr bw: dobel +
42 03.b. primitip adalah; 06. ………
48 2.1 dan 2.3
57 Letak Pers 2.34

i

KATA PENGANTAR

Puji syukur dipanjatkan kepada Tuhan Yang Mahaesa atas segala rahmat-Nya
sehingga penulisan buku FISIKA ZAT PADAT ini dapat diselesaikan.

Buku ini disusun atas dasar deskripsi matakuliah FIU 437 FISIKA ZAT
PADAT di Jurusan Fisika FMIPA Universitas Negeri Malang dan dengan maksud
agar perkuliahan matakuliah tersebut dapat berlangsung lebih efektif dan efisien.
Disamping itu, buku ini diharapkan dapat melengkapi pilihan pustaka mahasiswa
dalam memahami konsep dan gejala mendasar dalam zat padat.

Isi buku ini dirancang untuk kuliah satu semester dengan tiga sampai empat
kredit pada semester kedua tahun ketiga. Dengan demikian mahasiswa diharapkan
sudah menempuh matakuliah prasyaratnya, yaitu FISIKA KUANTUM dan FISIKA
STATISTIK.

Dalam setiap bab buku ini disajikan urutan subbab sedemikian rupa sehingga
memahami subbab sebelumnya menjadi bekal yang cukup baik untuk memahami
subbab sesudahnya. Oleh karena itu dalam mempelajari setiap bab buku ini
mahasiswa diharapkan membaca dan memahaminya mulai dari awal sampai akhir
secara berturutan.

Diucapkan terima kasih kepada semua pihak yang telah membantu sehingga
buku FISIKA ZAT PADAT ini dapat diselesaikan. Saran dan kritik membangun dari
para pembaca sangat diharapkan demi lebih sempurnanya buku ini.

Semoga buku ini berguna. Amin!
Malang, Pebruari 2006
Penyusun,

i

DAFTAR ISI
halaman

BAB I STRUKTUR KRISTAL
1.1 SIMETRI DAN STRUKTUR KRISTAL 2
1.1.1 Pengertian Pokok 2
1.1.1.1.Zat padat Kristal 2
1.1.1.2 Kisi Kristal 3
1.1.1.3 Vektor Basis 4
1.1.1.4 Sel Satuan Primitip dan Non-Primitip 4
1.1.1.5 Tiga Dimensi 5
1.1.2 Macam Dasar Kisi kristal 6
1.1.3 Beberapa Kristal dengan Struktur Sederhana 9
1.1.3.1 Struktur NaCl 9
1.1.3.2 Struktur CsCl 10
1.1.3.3 Struktur Intan 11
1.1.3.4 Struktur ZnS 12
1.1.3.5 Struktur HCP 12
1.1.4 Geometri Kristal 13
1.1.4.1 Arah kristal 13
1.1.4.2 Bidang Kristal dan Indek Miller 14
1.1.4.3 Jarak antar Bidang Sejajar 16
1.1.4.4 Fraksi Kepadatan 18
1.2 DIFRAKSI KISI KRISTAL 18
1.2.1 Hamburan Sinar-X oleh Kisi Kristal 19
1.2.1.1 Hukum Bragg 19
1.2.1.2 Teori Hamburan 20
1.2.1.3 Kisi Resiprok 23
1.2.1.4 Difraksi Sinar-X 24
1.3 IKATAN ATOMIK DALAM KRISTAL 28
1.3.1 Gaya Antaratom 28
1.3.2 Jenis Ikatan Kristal 30
1.3.2.1 Ikatan Ionik 30
1.3.2.2 Ikatan Kovalen 32
1.3.2.3 Ikatan Logam 34
1.3.2.4 Ikatan Van Der Walls 35
1.3.2.5 Ikatan Hidrogen 37
RINGKASAN 38
LATIHAN SOAL BAB I 41

ii

B A B II DINAMIKA KISI KRISTAL
2.1. GETARAN DALAM ZAT PADAT 47
2.1.1 Getaran Elastik dan Rapat Moda Getar 47
2.1.2 Kuantisasi Energi Getaran dalam Zat Padat 52
2.1.2.1 Model Einstein tentang Cv Zat Padat 53
2.1.2.2 Model Debye tentang Cv Zat Padat 56
2.2 GETARAN DALAM KISI KRISTAL 58
2.2.1 Getaran dalam Kisi Linier 58
2.2.1.1 Kisi Monoatomik Satu Dimensi 58
2.2.1.2 Kisi Diatomik Satu Dimensi 63
2.2.1.3 Kisi Tiga Dimensi 66
RINGKASAN 66
LATIHAN SOAL BAB II 68

BAB III ELEKTRON DALAM LOGAM I
(MODEL ELEKTRON BEBAS)
3.1 MODEL ELEKTRON BEBAS KLASIK 73
3.1.1 Teori Drude tentang Elektron dalam Logam 73
3.1.2 Model Elektron Bebas Klasik 76
3.2 MODEL ELEKTRON BEBAS TERKUANTISASI 78
3.2.1 Sumbangan Elektron Bebas pada Harga CV 80
3.2.2 Paramagnetik Pauli 82
3.2.3 Konduktivitas Listrik dalam Logam 83
3.3 PERILAKU ELEKTRON DALAM LOGAM 87
3.3.1 Hukum Matthiessen 87
3.3.2 Efek Hall 88
3.3.3 Resonansi Siklotron 90
3.3.4 Pancaran Termionik 91
3.4 KEBERATAN TERHADAP MODEL ELEKTRON BEBAS
TERKUANTISASI 93
RINGKASAN 94
LATIHAN SOAL BAB III 96

BAB IV LOGAM II (TEORI PITA ENERGI)
4.1 TEORI PITA ENERGI UNTUK ZAT PADAT 99
4.1.1 Teorema Bloch 100
4.1.2 Model Kronig-Penney 101
4.1.3 Pita Energi dan Energi Elektron dalam Atom 105
4.1.4 Refleksi Bragg dan Celah Energi 108
4.1.5 Logam, Isolator dan Semikonduktor 110
4.1.6 Metode LCAO 115
iii

4.2 DINAMIKA ELEKTRON DALAM KRISTAL 119
4.2.1 Kecepatan Kelompok dan Massa Efektif Elektron
dalam Kristal 119
4.2.2 Pengaruh Medan Listrik pada Kecepatan Elektron
dalam Kristal 125
4.2.3 Konduktivitas listrik 127
4.2.4 Dinamika Elektron dalam Medan Magnet 129
4.2.4.1 Efek Hall 129
4.2.4.2 Resonansi Siklotron 130
RINGKASAN 133
LATIHAN SOAL BAB IV 136

BAB V SEMIKONDUKTOR
5.1 KLASIFIKASI SEMIKONDUKTOR 140
5.2 SEMIKONDUKTOR INTRINSIK 140
5.3 SEMIKONDUKTOR EKTRINSIK 144
5.3.1 Ketidakmurnian Donor dan Akseptor 145
5.3.1.1 Donor 145
5.3.1.2 Aseptor 147
5.4 PENGUKURAN CELAH ENERGI
DENGAN METODE OPTIK 149
RINGKASAN 150
LATIHAN SOAL BAB V 152

BAB VI BAHAN DIELEKTRIK
6.1 RUMUSAN DASAR POLARISASI BAHAN 154
6.2 KONSTANTA DIELEKTRIK BAHAN
(PANDANGAN MAKROSKOPIS) 156
6.3 POLARISABILITAS BAHAN
(PANDANGAN MIKROSKOPIS) 157
6.3.1 Persamaan Clausius-Mosotti 157
6.3.2 Sumber Polarisabilitas 161
6.3.2.1 Polarisabilitas Polar 163
6.3.2.1.1 Polarisabilitas Polar Statik 163
6.3.2.1.2 Polarisabilitas Polar Bolak-balik 164
6.3.2.2 Polarisabilitas Ionik 167
6.3.2.3 Polarisabilitas Elektronik 170
6.3.2.3.1 Polarisabilitas Elektronik Statik 170
6.3.2.3.2 Polarisabilitas Elektronik Bolak-balik 171
6.4 GEJALA PIEZOELEKTRIK 172
6.5 GEJALA FERROELEKTRIK 173
RINGKASAN 173
LATIHAN SOAL BAB VI 178

iv

BAB VII BAHAN MAGNETIK
7.1 SUSEPTIBILITAS MAGNETIK BAHAN 183
7.2 GEJALA DIAMAGNETIK LANGEVIN 184
7.3 GEJALA PARAMAGNET 186
7.4 GEJALA MAGNETIK DALAM LOGAM 190
7.5 GEJALA FERROMAGNETIK 193
7.5.1 Gejala Ferromagnetik pada Isolator 193
7.5.1.1 Teori Medan Molekuler 193
7.5.1.2 Magnetisasi Spontan dan Hukum Curie-Weiss 194
7.5.2 Gejala Ferromagnetik pada Logam 197
7.6 GEJALA ANTIFERROMAGNETIK
DAN FERRIMAGNETIK 198
RINGKASAN 199
LATIHAN SOAL BAB VII 201

DAFTAR RUJUKAN

v

BAB I
STRUKTUR KRISTAL

Zat padat, yang terlihat sebagai benda tegar padat, secara mikro terdiri dari
atom. Atom-atom zat padat tidaklah diam, melainkan bervibrasi dengan amplitudo
kecil di sekitar titik kesetimbangannya. Karena posisinya yang relatif tetap, maka
atom-atom tersebut cenderung membentuk struktur tertentu. Hal ini berbeda
dengan cairan atau gas, yang mana atom-atomnya bergerak pada jarak yang lebih
besar sehingga strukturnya tidak tertentu.
Distribusi setimbang atom-atom mendefinisikan struktur padatan, yang
terdiri dari tiga bagian besar, yaitu kristalin, amorf, dan polikristal. Dalam zat
padat kristal, atom tersebut terdistribusi teratur relatif terhadap yang lain.
Terdapat beberapa jenis struktur kristal yang bergantung pada geometri susunan
atom. Pemahaman tentang struktur kristal bahan adalah hal penting dalam fisika
zat padat, karena, umumnya, struktur kristal mempengaruhi sifat zat padat. Zat
padat polikristal dibentuk oleh sejumlah besar kristal-kristal kecil, yang disebut
kristalin. Atom-atom membentuk pola dalam suatu kristal, tetapi orientasinya
akan lenyap pada batas kristalin. Sedangkan dalam zat padat amorf, terjadi
distribusi atom secara acak. Bahan-bahan zat padat dapat berbentuk kristalin,
polikristal atau amorf, bergantung pada bagaimana bahan tersebut dipreparasi.
Selanjutnya, dalam diktat ini hanya dibahas zat padat kristal saja.

I STRUKTUR KRISTAL 2

Bagian awal bab ini menyajikan pengertian struktur kristal beserta
perluasannya melalui rumusan dasar matematika. Kemudian dibahas jenis struktur
yang mungkin, dan dikenalkan konsep indek Miller. Struktur kristal dapat
ditentukan dengan menggunakan difraksi sinar-X. Bab ini ditutup oleh bahasan
gaya antaratom yang menyebabkan terjadinya ikatan dalam kristal.

1.1 SIMETRI DAN STRUKTUR KRISTAL

1.1.1 Pengertian Pokok

1.1.1.1 Zat Padat Kristal
Suatu benda padat berbentuk kristal, apabila atom, ion, atau molekulnya
(selanjutnya disebut atom saja) teratur dan periodik dalam rentang yang panjang
dalam ruang. Kristal sempurna mempunyai keperiodikan tak berhingga. Namun,
kenyataannya, tidak mungkin mempreparasi kristal sempurna karena berbagai
keterbatasan fisis, yaitu (a) adanya permukaan kristal, (b) cacat geometrik, (c)
ketakmurnian, dan (d) pada suhu T>0 K atom dalam kristal bergetar harmonik di
sekitar titik setimbangnya.
Gambar 1.1 berikut menyajikan geometri kristal dua dimensi.

b R

a

Gambar 1.1 Zat padat kristal. Seluruh atom tersusun periodik.
Kedudukan dalam ruang dua dimensi di atas merupakan kedudukan atomnya.
Setiap titik di dalamnya terletak pada ujung vektor kisi
R = n1 a + n2 b (1.1)

dengan (n1, n2) adalah pasangan bilangan bulat; dan a dan b adalah vektor basis.

Fisika Zat Padat Parno – Fisika FMIPA UM


Bahan kristal memiliki simetri translasi, artinya seluruh kristal itu digeser
sejauh vektor R di atas (yang menghubungkan dua buah atomnya), maka
keadaannya tetap sama. Dengan kata lain kristal bersifat invarian terhadap
translasi semacam itu.

1.1.1.2 Kisi Kristal
Dalam kristalografi (bahasan geometri kristal), setiap atom dalam kristal
dianggap sebagai suatu titik, tepat pada kedudukan setimbang tiap atom itu di
dalam ruang. Pola geometrik yang diperoleh dinamakan kisi kristal.
Terdapat dua kelas kisi, yaitu Bravais dan non-Bravais. Dalam kisi
Bravais, seluruh titik kisi adalah ekivalen, artinya kisi bersifat invarian terhadap
operasi simetri translasi. Dengan demikian semua atom dalam kristal haruslah
sejenis. Sedangkan dalam kisi non-Bravais terdapat beberapa titik kisi yang tidak
ekivalen.
Gambar 1.2 berikut menyajikan kisi non-Bravais.

Gambar 1.2 Kisi non-Bravais dengan basis A dan A’
Tempat kisi A, B dan C adalah ekivalen, begitu juga A’, B’ dan C’. Tetapi, dua
tempat kisi A dan A’ tidak ekivalen karena kisi tidak invarian terhadap translasi
sepanjang AA’. Kisi non-Bravais seringkali disebut sebagai kisi dengan suatu
basis. Basis yang dimaksud adalah kumpulan atom yang ditempatkan di sekitar
titik kisi Bravais. Dalam Gambar 1.2 di atas basisnya adalah A dan A’.
Kisi non-Bravais dapat dipandang sebagai kombinasi dari dua atau lebih
kisi Bravais yang saling menembus dengan orientasi tertentu.



1.1.1.3 Vektor Basis
Lihat kembali Gambar 1.1. Posisi semua titik kisi dinyatakan oleh
persamaan (1.1), yakni R = n1 a + n2 b . Perhatikanlah bahwa a dan b , yang
dinamakan vektor basis, (a) bersifat tidak unik, dan (b) haruslah tidak kolinier.

1.1.1.4 Sel Satuan Primitip dan non-Primitip
Luas daerah jajaran genjang (paralelogram) yang sisinya dibatasi oleh
vektor basis disebut sel satuan, seperti luasan daerah bayang-bayang dalam
Gambar 1.3 berikut.

b R

a

Gambar 1.3 Vektor a dan b membentuk sel satuan

Sel satuan merupakan dasar pola elementer karena berulang secara periodik dan
membentuk struktur kisi suatu kristal. Bila sel satuan tersebut dilakukan translasi
oleh vektor kisi R di atas, maka seluruh kisi kristal tercakup olehnya. Luas daerah

paralelogram dengan sisi a dan b adalah a × b =ab sin γ, dimana γ adalah sudut

antara a dan b .
Perhatikanlah bahwa sel satuan itu (a) tidak unik, (b) setiap sel satuan
mempunyai luasan yang sama, dan (c) dalam contoh di atas sel satuan
mengandung satu titik kisi.
Yang dibicarakan di atas adalah sel primitip, yakni sel satuan yang hanya
mengandung satu titik kisi perselnya. Sedangkan sel non-primitip memiliki lebih
dari satu titik kisi perselnya. Vektor basis yang membentuk sel satuan primitip
disebut vektor basis primitip; dan sel satuan non-primitip disebut vektor basis
non-primitip. Gambar 1.4 berikut memperjelas perbedaan keduanya.



2

1

5
3
4

Gambar 1.4 Sel primitip (3, 4 dan 5) dan
non-primitip (1 dan 2 dengan dua titik kisi persatuan sel)
Perhatikanlah bahwa jika sel satuannya adalah sel primitip, maka titik-titik
kisi hanya ada pada tiap-tiap pojok jajaran genjang, yaitu sebanyak 4 titik kisi.
Setiap titik kisi menjadi milik bersama antara 4 buah sel, sehingga jumlah total
titik kisi dalam sel satuan primitip sebanyak 4x¼=1. Hal demikian tidak terjadi
pada sel satuan nonprimitip.
Beberapa hal penting yang berkaitan dengan sel satuan adalah (a) sel non-
primitip menunjukkan simetri lebih besar, (b) luas sel non-primitip merupakan
kelipatan bulat dari luas sel primitip, dan (c) sel primitip dan non-primitip berkait
dengan pemilihan vektor basis dalam kisi Bravais.

1.1.1.5 Tiga Dimensi
Bahasan kristal dalam tiga dimensi sama dengan dalam dua dimensi,
hanya keadaannya ditambah dengan satu dimensi lagi. Disamping itu, hal yang
perlu diperhatikan adalah
(a) ungkapan vektor basis menjadi
R = n1 a + n2 b + n3 c (1.2)

dengan vektor basis (a , b , c ) yang tidak koplanar,
(b) vektor basis membentuk sel satuan volume berbentuk paralelepipidum,



(c) antarvektor basis satu sama lain membentuk sudut α, β dan γ seperti terlihat
pada Gambar 1.5 berikut.

(d) volume paralelepipidum dengan sisi
a , b dan c adalah luas bagian

dasar berbentuk paralelogram a × b

yang dikalikan dengan komponen c
sepanjang sumbu yang tegak lurus
terhadap bagian dasar tersebut, yaitu
Gambar 1.5 Kisi tiga dimensi dengan
V = c • a ×b .
vektor basis (a , b , c )

dan sudut α, β, γ antaranya
Perhatikanlah bahwa sel satuan pada Gambar 1.5 adalah sel satuan
primitip, yaitu titik-titik kisi berjumlah 8 hanya ada pada tiap pojok
paralelepipidum. Setiap titik kisi menjadi milik bersama sebanyak 8 sel satuan,
sehingga jumlah total titik kisi dalam sel satuan primitip tersebut sebanyak
8x 1 =1. Hal demikian tidak terjadi pada sel satuan nonprimitip.
8

1.1.2 Macam Dasar Kisi Kristal
Kondisi simetri translasi dalam kristal mempunyai konsekwensi terhadap
terbatasnya kemungkinan jenis kisi Bravais yang dapat terjadi, baik dalam kisi
kristal dua maupun tiga dimensi.
Dalam dua dimensi, kisi kristal yang mungkin sebanyak lima jenis, seperti
terlihat dalam Tabel 1.1 dan Gambar 1.6 berikut.
Tabel 1.1 Macam kisi dua dimensi
No Kisi Sel Satuan Sisi dan Sudut
1 Genjang Jajaran genjang a≠b ϕ ≠ 900
2 Persegi Bujur sangkar a=b ϕ = 900
3 Heksagonal Belah ketupat a=b ϕ = 1200
4 Empat persegi panjang P Empat persegi panjang a≠b ϕ = 900
5 Empat persegi panjang I Empat persegi panjang a≠b ϕ = 900



a a

a a

b b b
a a a

Gambar 1.6 Lima jenis dasar kisi Bravais dua dimensi
Tampak bahwa hanya kisi empat persegi panjang I yang memiliki sel satuan
nonprimitip
Untuk kasus tiga dimensi ternyata ada 14 buah kisi Bravais yang
terlingkupi dalam 7 buah sistem kristal. Hal ini sebagai konsekuensi dari simetri
rotasi sebuah kristal, yakni rotasi-1, 2, 3, 4, dan 6, seperti disajikan dalam Tabel
1.2 dan Gambar 1.7 berikut.
Tabel 1.2 Macam kisi tiga dimensi
Sistem
No Kisi Bravais Geometri Kristal Simetri Khas
Kristal
1 Triklinik P a≠b≠c α≠β≠γ Tidak ada
2 Monoklinik P , C a ≠ b ≠ c α = β = 900 γ ≠ 900 Sebuah sumbu rotasi-2
Tiga sumbu rotasi-2
3 Ortorombik P , C, I, F a ≠ b ≠ c α = β = γ = 900
ortogonal
4 Tetragonal P , I a = b ≠ c α = β = γ = 900 Sebuah sumbu rotasi-4
a = b = c α = β = γ < 1200
5 Trigonal R Sebuah sumbu rotasi-3
tetapi bukan 900
6 Heksagonal P a = b ≠ c α = β = 900 γ = 1200 Sebuah sumbu rotasi-3
Empat sumbu rotasi-3
7 Kubik P, I,F a = b = c α = β = γ = 900 sepanjang diagonal
kubus
Kisi Bravais P, C, I, F, dan R, masing-masing mengandung jumlah titik kisi persel
satuannya adalah 1, 2, 2, 4, dan 1.



Gambar 1.7 Empat belas kisi Bravais berdimensi tiga
dan distribusinya dalam 7 sistem kristal
P = primitip C = “base centered”
I = “body Centered” F = “face centered”
R = rombohedral primitip



1.1.3 Beberapa Kristal dengan Struktur Sederhana

1.1.3.1 Struktur Sodium Khlorida (NaCl)
Na Cl mempunyai struktur FCC dengan basis satu atom Na dan satu atom
Cl yang terpisah sepanjang setengah diagonal ruang kubus. Sepanjang ketiga arah
sumbu utama kubiknya terdapat alternasi atom Na dan Cl, seperti ditunjukkan
oleh Gambar 1.8 berikut.

Gambar 1.8 Struktur NaCl tiga dimensi
Setiap sel satuan memiliki 4 perangkat NaCl yang atomya berkedudukan di
Cl : 000 ½½0 ½0½ 0½½
Na: ½½½ 00½ 0½0 ½00
Jika sisi kubik adalah a, maka kedua atom dalam basis terpisah sejauh ½√3a, dan
setiap atom memiliki 6 atom tetangga terdekat yang berbeda jenis dengan jarak
pisah masing-masing ½a. Nilai konstanta a untuk NaCl berharga 5,63 Å.

NaCl dapat pula dipandang sebagai struktur non-Bravais, yang terdiri dari
dua subkisi FCC, masing-masing untuk Na dan Cl, yang saling menembus. Kedua
subkisi tersebut terpisah sejauh ½a satu sama lain.



Beberapa kristal yang memiliki struktur NaCl adalah LiH, MgO, MnO,
AgBr, PbS, KCl, dan KBr dengan konstanta kisi masing-masing 4,08; 4,20; 4,43;
5,77; 5,92; 6,29; dan 6,59 Å.

1.1.3.2 Struktur Sesium Khlorida (CsCl)
CsCl memiliki struktur SC dengan basis satu atom Cs dan satu atom Cl.
Alternasi atom Cs dan Cl terdapat sepanjang diagonal ruang kubik, seperti terlihat
pada Gambar 1.9 berikut.

Gambar 1.9 Struktur CsCl
Setiap sel satuan mengandung satu molekul CsCl, dengan posisi atom
Cs : 000 Cl : ½½½
CsCl dapat pula dipandang sebagai struktur non-Bravais yang terdiri dari
dua subkisi SC (kubik sederhana), yang masing-masing dibentuk oleh atom-atom
Cs dan Cl, yang keduanya terpisah sejauh ½√3a (setengah diagonal ruang).
Jumlah titik terdekat setiap atom adalah 8 atom yang berbeda jenis. CsCl memiliki
konstanta kisi 4,11 Å.
Beberapa kristal yang memiliki struktur CsCl adalah BeCu, AlNi, CuZn,
CuPd, AgMg, LiHg, NH4Cl, TlBr, dan TlI dengan konstanta kisi masing-masing
2,70; 2,88; 2,94; 2,99; 3,28; 3,29; 3,87; 3,97; dan 4,20 Å.



1.1.3.3 Struktur Intan
Struktur intan dapat dilihat sebagai struktur yang sel satuannya adalah sel
FCC dengan suatu basis, yakni dua atom C yang posisinya
000 dan ¼¼¼
seperti terlihat pada Gambar 1.10 dan 1.11 berikut.

Gambar 1.10 Struktur kristal intan dengan ikatan tetrahedralnya

Gambar 1.11 Proyeksi posisi atom dalam struktur intan sel kubik
pada salah satu sisi kubik. Bilangan pecahan menunjukkan
ketinggian di atas bidang dasar



Dalam setiap sel satuan terdapat 8 atom C dan bilangan koordinasinya adalah 4.
Keempat atom terdekat membentuk suatu tetrahedral, dengan pusat atom yang
bersangkutan. Konfigurasi semacam itu sering dijumpai pada semikonduktor, dan
dinamakan ikatan tetrahedral. Struktur intan merupakan contoh ikatan kovalen
dalam unsur-unsur kolom IV tabel periodik.

Struktur intan dapat pula dipandang sebagai gabungan dari dua subkisi
FCC yang saling menembus dengan titik asal, masing-masing 000 dan ¼ ¼ ¼.

Beberapa kristal yang memiliki struktur intan adalah Ge, Si, C, timah putih
dengan konstanta kisi masing-masing 5,65; 5,43; 3,56; dan 6,46 Å.

1.1.3.4 Struktur Seng Sulfida (ZnS)
Struktur ZnS sama dengan struktur intan, tetapi dengan basis yang terdiri
dari dua atom berbeda, yakni Zn dan S. Setiap sel satuan memiliki 4 molekul ZnS
dengan posisi atom
Zn : 000 0½½ ½0½ ½½0
S: ¼¼¼ ¼¾¾ ¾¼¾ ¾¾¼
Setiap atom memiliki jarak yang sama terhadap keempat atom yang berbeda
terdekatnya yang menempati pojok-pojok tetrahedron regular. ZnS memiliki
konstanta kisi 5,41 Å.
Beberapa kristal yang memiliki struktur ZnS adalah CuF, SiC, CuCl, AlP,
GaP, ZnSe, GaAs, AlAs, CdS, InSb, dan AgI dengan konstanta kisi masing-
masing 4,26; 4,35; 5,41; 5,45; 5,45; 5,65; 5,65; 5,66; 5,82; 6,46; dan 6,47 Å.

1.1.3.5 Struktur HCP (hexagonal close-packed structure)
Banyak cara untuk menyusun bola identik dengan jumlah tak berhingga
secara tertentu sehingga menghasilkan susunan teratur yang memiliki fraksi
kepadatan maksimum atau ruang kosong antarbola minimum. Gambar 1.12
berikut melukiskan susunan satu lapis bola identik dengan pusat titik A, yang
mana tiap bola bersinggungan dengan enam bola tetangga terdekatnya. Lapisan
kedua yang identik ditempatkan paralel di atasnya (lapisan pertama) dengan pusat
titik B. Penempatan lapisan ketiga memiliki dua kemungkinan, yakni



Gambar 1.12 Lapisan bola terkemas rapat dengan pusat titik A
(a) dengan pusat titik A, sehingga terdapat urutan lapisan ABABAB…, dan
menghasilkan struktur HCP, dan
(b) dengan pusat titik C, sehingga terdapat urutan ABCABC…, dan menghasilkan
struktur FCC.
Lapisan pertama A merupakan bidang dasar untuk struktur HCP atau
bidang (111) untuk struktur FCC. Struktur HCP memiliki sel primitip kisi
heksagonal, tetapi dengan basis dua atom. Sedangkan sel primitip FCC berbasis
satu atom.
Baik HCP maupun FCC mempunyai perbandingan c/a= 2 6 =1,633 dan
3

jumlah tetangga terdekat 12 buah atom, serta energi ikatan yang hanya bergantung
pada jumlah ikatan tetangga terdekat peratom.
Beberapa kristal yang memiliki struktur HCP adalah He, Be, Mg, Ti, Zn,
Cd, Co, Y, Zr, Gd, dan Lu dengan nilai c/a masing-masing adalah 1,633; 1,581;
1,623; 1,586; 1,861; 1,886; 1,622; 1,570; 1,594; 1,592; dan 1,586.

1.1.4 Geometri Kristal

1.1.4.1 Arah Kristal
Telah dikemukakan bahwa arah tertentu dalam kisi dinyatakan oleh vektor
kisi (1.2), yaitu R = n1 a + n 2 b + n3 c . Arah vektor R dinyatakan dengan [n1 n2
n3], yang lazimnya dalam perbandingan bilangan bulat terkecil. Semua arah yang



sejajar memiliki indek yang sama. Perhatikanlah beberapa arah dalam kristal
ortorombik seperti Gambar 1.13 berikut.

c D
C

B

O
b

a A

Gambar 1.13 Indek arah satuan sel ortorombik
OA: [110] OB: [111] OC: [112] OD: [001]
Apabila sel satuan yang ditinjau mempunyai simetri rotasi, maka
seringkali ada arah nonparalel yang karena kesimetriannya merupakan arah yang
ekivalen. Arah [n1 n2 n3] yang ekivalen menggunakan notasi <n1 n2 n3>. Misalnya,
pada suatu kubik sumbu X, Y dan Z masing-masing memiliki arah [100], [010]
dan [001] yang ekivalen, dinotasikan dengan <100>. Secara sepenuhnya <100>
mencakup arah [100], [010], [001], [ 1 00], [0 1 0] dan [00 1 ] dimana makna dari
1 adalah –1; dan <111> menunjukkan semua diagonal ruang suatu kubik.
Satu arah dengan indeks Miller besar, misalnya [157], memiliki jumlah
atom persatuan panjang yang lebih sedikit daripada indeks yang kecil, misalnya
[111].

1.1.4.2 Bidang Kristal dan Indek Miller
Representasi suatu bidang datar dalam suatu kisi kristal diungkapkan oleh
indek Miller (hkl). Perhatikanlah Gambar 1.14 berikut.



Gambar 1.14 Bidang (233)

Bidang memotong sepanjang sumbu vektor basis a , b dan c masing-masing pada

⎛x y z⎞
x, y dan z. Didapatkan perangkat tiga bilangan ⎜ ⎟ . Lalu, diambil
⎝a b c⎠
⎛a b c⎞
kebalikannya, yaitu ⎜
⎜ x y z ⎟ . Indek Miller didapatkan dengan menyatakan
⎟
⎝ ⎠
perangkat tiga bilangan terakhir sebagai perbandingan bilangan bulat terkecil, dan
dinyatakan dengan notasi
⎛ a c⎞
(h k l) = ⎜m
⎜ x m
b
m ⎟ (1.3)
⎝ y z⎟
⎠
dengan m adalah bilangan bulat untuk mereduksi indek menjadi bilangan bulat
terkecil. Dengan demikian, kumpulan bidang paralel mempunyai representasi
indek Miller yang sama. Pada Gambar 1.14 di atas x=3a, y=2b dan z=2c, sehingga
jika dianggap a=b=c=1, maka bidang yang dimaksud memiliki indek Miller
(hkl)=(233). Pada kasus lain, misalnya x=2a, y=(3/2)b, dan z=c memiliki indeks
Miller (hkl)=(346).
Dalam satuan sel yang memiliki simetri rotasi, beberapa bidang nonparalel
(hkl) adalah ekivalen karena kesimetriannya, dan dinotasikan dengan {hkl}.
Misalnya dalam sistem kubik indek {100} menunjukkan enam bidang, yaitu
(100), (010), (001), ( 1 00), (0 1 0) dan (00 1 ).



Berikut adalah beberapa contoh bidang (hkl) dalam sistem kubik.

Gambar 1.15 Bidang (100), (110), (111), (200) dan ( 1 00)
dalam sistem kubik
Dalam koordinat Kartesis bidang (hkl) = (mnox mnoy mnoz) memberikan
vektor arah yang tegak lurus terhadap bidang tersebut, yakni
ˆ j ˆ
no = nox i + noy ˆ + noz k .

1.1.4.3 Jarak Antarbidang Sejajar Miller
Bahasan ini dibatasi pada sistem dengan sumbu ortogonal, dengan a≠b≠c.
Perhatikanlah Gambar 1.16 berikut.



Z

z Garis normal

γ

β y Y

α
x
X

Gambar 1.16 Cara mendapatkan jarak antarbidang Miller

Jarak dari titik O ke titik potong P dinayatakan dengan dhkl. Jika x, y dan z
merupakan titik potong bidang (hkl) dengan sumbu a, b dan c maka dhkl=x cos
α=y cos β=z cos γ. Secara geometri, pada gambar di atas didapatkan hubungan
cos2α+ cos2 β+ cos2 γ=1 sehingga didapatkan
1
d hkl = 1/ 2
(1.4)
⎛ 1 1 1 ⎞
⎜ 2 + 2 + 2⎟
⎜x
⎝ y z ⎟⎠
Harga x, y dan z berkaitan dengan bilangan h, k dan l melalui ungkapan
a b c
h=m ; k=m ; l=m (1.5)
x y z
sehingga jarak antarbidang (1.4) menjadi
m
d hkl = 1/ 2
(1.6)
⎛ h2 k 2 l 2 ⎞
⎜ 2 + 2 + 2⎟
⎜a
⎝ b c ⎟ ⎠
Misalnya, pada sistem kubik dengan sisi a didapatkan d111=(1/3)√3a; d110=½√2a
dan d020=½a. Pada umumnya bidang yang indek Millernya rendah memiliki jarak
antarbidang lebih besar, tetapi memiliki kerapatan atom persatuan luas yang lebih
besar.



1.1.4.4 Fraksi Kepadatan
Fraksi kepadatan, didefinisikan sebagai proporsi maksimum dari volume
yang ada yang dapat diisi oleh bola atom dalam sebuah sel satuan, diungkapkan
dalam bentuk rumusan

F=N
(4 / 3)π r3
(1.7)
V
dengan N= jumlah atom dalam sel satuan
r = jari-jari bola atom
V = volume sel satuan
Jarak kesetimbangan antara pusat dua atom berdekatan dapat dipandang sebagai
jumlah jari-jari kedua atom tersebut.
Tabel 1.3 berikut menunjukkan hubungan antara struktur kristal dengan
ukuran geometrik sel satuan.
Tabel 1.3 Ukuran geometrik dan struktur kristal
No Parameter SC BCC FCC Intan HCP
1 Jari-jari atom a/2 a√3/4 a√2/4 a√3/8 a/2
2 Atom persel satuan 1 2 4 8 6
3 3
3 Volume sel satuan a a a3 a3 3a3√2
π/6 π√3/8 π√2/6 π√3/16 π√2/6
4 Fraksi kepadatan
(=0,524) (=0,68) (=0,74) (=0,34) (=0,74)
Jumlah tetangga
5 6 8 12 4 12
terdekat
Jarak terhadap
6 a (½)a√3 (½)a√2 (¼)a√3 a
tetangga terdekat
Jumlah tetangga
7 12 6 6 12 6
terdekat berikutnya
Jarak terhadap
8 tetangga terdekat a√2 a a (½)a√13 a√3
berikutnya
Tampak bahwa intan memiliki struktur yang relatif kosong (hanya terisi 0,34) dan
FCC atau HCP relatif padat (terisi 0,74).

1.2 DIFRAKSI KISI KRISTAL

Struktur kristal dapat dipelajari melalui difraksi foton, netron dan elektron.
Panjang gelombang optik, misalnya 5000 Å, menghasilkan gelombang terhambur



elastis dengan atom-atom kristal sehingga terjadi refraksi optik biasa. Tetapi, jika
panjang gelombang radiasi sebanding atau lebih kecil daripada konstanta kisi
(orde angstrom), maka didapatkan berkas difraksi yang arahnya sangat berbeda
dengan arah berkas datang.

1.2.1 Hamburan Sinar-X oleh Kisi Kristal

1.2.1.1 Hukum Bragg
W.L. Bragg menjelaskan gejala berkas difraksi kristal dengan model
sederhana. Jika sinar-X mengenai permukaan suatu kristal, maka terjadi refleksi.
Model disajikan pada Gambar 1.17, yakni kristal direpresentasikan oleh kumpulan
bidang paralel yang bersesuaian dengan bidang atom. Bidang tersebut berperan
sebagai cermin. Setiap bidang hanya merefleksikan 10-3 sampai 10-5 radiasi yang
datang sehingga diperlukan 103 sampai 105 bidang untuk menghasilkan berkas
refleksi Bragg yang sempurna. Hamburan ini dianggap elastik, yakni energi sinar-
X tidak mengalami perubahan sebelum dan sesudah refleksi.

(a) (b)
Gambar 1.17 (a) Refleksi sinar-X dari suatu kristal. Sinar hampir paralel karena
posisi detektor jauh dari kristal.
(b) Intensitas refleksi kristal KBr. Pada gambar ditunjukkan
bidang-bidang refleksi yang menghasilkan difraksi
Beda lintasan untuk kedua sinar refleksi adalah Δ=AB + BC – AC’ = 2 AB – AC’
karena AB=BC. Mengingat jarak antarbidang d, maka
AB = d/sinθ dan AC’ = AC cos θ = (2d/tg θ) cos θ



dimana θ adalah sudut pantul antara berkas datang dan bidang refleksi, sehingga
Δ = 2 d sin θ. Interferensi maksimum (konstruktif) terjadi hanya jika
Δ=nλ (1.8)
dimana n = 1, 2, 3, …. (ordo refleksi) dan λ = panjang gelombang sinar-X,
sehingga diperoleh hukum Bragg untuk refleksi oleh bidang kristal (hkl)
n λ = 2 dhkl sin θ (1.9)
Harga λ ditentukan secara bebas dan sin θ diukur secara langsung dari refleksi
eksperimen, sehingga jarak antarbidang dhkl dapat dihitung. Hal lain adalah
difraksi hanya mungkin terjadi jika λ<2d. Oleh karena itu dalam hal ini tidak
dapat digunakan cahaya tampak.
Model yang dikemukakan di atas terlalu sederhana. Fakta menunjukkan
bahwa hamburan berkas sinar-X disebabkan oleh atom diskrit kristal yang
bersangkutan. Oleh karena itu bahasan berikut menelaah hukum Bragg melalui
proses hamburan.

1.2.1.2 Teori Hamburan
Hamburan radiasi elektromagnet oleh suatu elektron disajikan oleh
Gambar 1.18 berikut. Dalam proses ini diandaikan hamburan bersifat elastik
(hamburan Thomson).

Gambar 1.18 Hamburan oleh elektron tunggal
Gelombang datar

ψ (r , t ) = Ae i (k o • r −ω t ) (1.10)
mengenai elektron. Gelombang sferik terhambur pada jarak radial D dinyatakan
oleh



ψ ' (D , t ) = f e
A i (kD −ω t )
e (1.11)
D
dengan fe adalah panjang hamburan elektron. Terlihat bahwa penurunan
amplitudo gelombang terhambur sebanding dengan 1/D.
Hamburan oleh sistem dua elektron, yang masing-masing berkedudukan di
P1 dan P2 disajikan pada Gambar 1.19 berikut.

k s

2θ
ko

Gambar 1.19 Hamburan oleh dua elektron. r Gambar 1.20 Vektor hamburan s .
adalah vektor posisi elektron-1 terhadap Sudut 2θ adalah sudut hamburan
elektron-2

Didefinisikan vektor hamburan s , seperti pada Gambar 1.20, yaitu
s = k − ko (1.12)

Karena hamburan bersifat elastik k o = k = k , maka terlihat dari Gambar 1.20

bahwa
s = s = 2k sin θ (1.13)

Beda panjang lintasan sinar terhambur Δ=P1M- P1N. Jika S o dan S , masing-

1
masing merupakan vektor satuan dalam arah k o dan k , maka Δ = (r • s ) . Beda
k
fasa antara gelombang terhambur dalam radial
Δ
δ = 2π = kΔ = r • s (1.14)
λ
Superposisi dari dua gelombang terhambur dalam fungsi ruang

ψ T = fe
D
(
A ikD A
) (
e + e ik ( D +δ ) = f e e ikD 1 + e is •r
D
) (1.15)



Secara umum, bila vektor posisi r1 untuk elektron-1 dan r2 untuk elektron-2
relatif terhadap pusat tertentu, maka

ψ T = fe
D
e e (
A ikD is •r1
+ e is •r2 ) (1.16)

Bila yang ditinjau atom dengan l buah elektron, masing-masing dengan
vektor posisi rl , dengan l = 1, 2, 3, …, n, maka bentuk umum gelombang untuk

(1.16) dalam arah terhambur s tertentu
A ikD
ψT = f e (1.17)
D
dengan
n
f = f e ∑ e is •rl (1.18)
l =1

disebut panjang hamburan total.
Intensitas parsial gelombang terhambur I sebanding dengan kuadrat
besarnya medan. Oleh karena itu
n 2

= f e2 ∑ e is •rl
2
I∞ f (1.19)
l =1

Jika atom dalam kristal, misalnya, terletak pada posisi Rl , maka faktor
hamburan kristal fkr
N
f kr = ∑ f al e is • Rl (1.20)
l =1

Ungkapan faktor hamburan kristal (1.20) di atas mengambil bentuk analogi dari
atom. Posisi atom dapat ditinjau dalam sel satuannya, yaitu Rl = Rlc' + δ j , dimana

Rlc' adalah posisi sel satuan ke-l, dan δj adalah posisi atom dalam sel satuan,

sehingga faktor hamburan kristal (1.20) di atas dapat dinyatakan dalam bentuk
faktorisasi
fkr = F S (1.21)

dengan F = ∑ f aj e dan S = ∑ e
is •δ j is • Rlc'
(1.22)
j l'



F dan S, masing-masing mengungkapkan faktor struktur geometri dan kisi. Faktor
struktur kisi hanya bergantung pada sistem kristal. Sedangkan faktor struktur
geometri bergantung pada bentuk geometri dan isi sel satuan.

1.2.1.3 Kisi Resiprok
Setiap struktur kristal memiliki 2 kisi, yaitu kisi kristal dan resiprok. Saat
kristal dikenai sinar-X, akan dihasilkan pola difraksi yang merupakan peta kisi
resiprok kristal tersebut. Kedua kisi ini memiliki relasi sebagai berikut.
Andaikanlah vektor basis dalam kisi nyata adalah a , b dan c , maka dapat
didefinisikan vektor basis dalam kisi resiprok, yakni
b xc c xa axb
a ∗ = 2π b ∗ = 2π c ∗ = 2π (1.23)
a • b xc b • c xa c • axb
Hal ini berarti vektor basis resiprok
a. memiliki satuan m-1, yang sama dengan angka gelombang,
( )
b. bahwa a ∗ tegak lurus terhadap bidang b , c , dan demikian pula permutasi
siklisnya, dan
c. bahwa a • b xc = b • c xa = c • axb merepresentasikan volume sel satuan dengan
rusuk vektor a , b dan c .
Vektor basis resiprok mendefinisikan vektor kisi resiprok
Gn = n1 a ∗ + n2 b ∗ + n3 c ∗ (1.24)
dengan n1, n2 dan n3 adalah bilangan bulat.
Kisi resiprok memiliki hubungan dengan kisi nyata sebagai berikut.
a. a ∗ • a = b ∗ • b = c ∗ • c = 2π

b. V ∗
=
(2π )3 , dengan Vo = a • b xc dan Vo∗ = a ∗ • b ∗ xc ∗
o
Vo

c. Setiap vektor dari kisi resiprok Ghkl = ha ∗ + kb ∗ + lc ∗ tegak lurus terhadap
bidang kisi (hkl) dalam ruang nyata.
d. Kisi nyata merupakan resiprok dari kisi resiprok.
e. Jarak antarbidang dhkl dan Ghkl direlasikan oleh



d hkl Ghkl = 2π (1.25)

Perhatikanlah perbandingan kisi nyata dan resiproknya pada Gambar 1. 21
berikut.

120

d100
010
G110

d010 b*
O 100
b a*

O a

Gambar 1.21 Perbandingan kisi nyata dan resiproknya
Dari Gambar 1.21 di atas jelaslah bahwa
a. a ∗ tegak lurus terhadap b ; dan b ∗ tegak lurus terhadap a
2π 2π 2π
a∗ = = b∗ =
a d100 d 010

b. setiap titik (hkl) dalam ruang resiprok terkait dengan perangkat bidang (hkl)
dalam ruang nyata, dan
c. simetri kelompok titik dalam ruang resiprok sama dengan simetri ruang nyata.
Dapat pula dibuktikan bahwa terdapat hubungan sebagai berikut.
a. Kisi resiprok kisi SC adalah kisi SC juga.
b. Kisi resiprok kisi BCC adalah kisi FCC; dan sebaliknya.

1.2.1.4 Difraksi Sinar-X
Kisi resiprok berguna dalam menentukan besarnya faktor struktur.
Ternyata
N

∑e
l =1
iA• Rlc'
= N δ A,G
n
(1.26)



Dalam hal ini A adalah vektor sebarang dan penjumlahan dilakukan sepanjang
vektor kisi nyata yang mengandung N buah total sel dan vektor kedudukan Rlc' .

Dengan demikian faktor struktur kisi S (1.22) berharga nol untuk setiap nilai
vektor hamburan s , kecuali
s = Ghkl (1.27)

Hal ini berarti s harus tegak lurus terhadap bidang (hkl). Dengan menginat
bahwa k=2π/λ, maka substitusi persamaan (1.13) dan (1.25) ke dalam persamaan
(1.27), dalam teori hamburan ini, menghasilkan bentuk hukum Bragg
2 dhkl sin θ = λ (1.28)
Dapatlah dikatakan bahwa gambaran Bragg tentang difraksi yang terjadi karena
pemantulan oleh bidang kristal, secara konseptual lebih sederhana daripada
melihatnya sebagai interferensi konstruktif berkas terhambur oleh atom kristal
dari teori hamburan. Gambar 1.22 berikut menjelaskan syarat terpenuhinya hukum
Bragg menurut teori hamburan.

Gambar 1.22 Vektor hamburan sama dengan vektor kisi resiprok

Saat kondisi Bragg (127) terpenuhi, maka faktor struktur kisi S≠0, tetapi
bernilai S=N, seperti tampak pada (1.26), sehingga
Shkl = N (1.29)
Substitusi (1.29) ke dalam (1.21) menghasilkan faktor hamburan kristal fkr
menjadi
fkr,hkl = N Fhkl (1.30)
dan intensitas I menjadi



2 2
I hkl ∞ f kr ,hkl ∞ Fhkl (1.31)

Setiap berkas terdifraksi bersesuaian dengan suatu perangkat bidang (hkl).
Tetapi untuk suatu perangkat bidang (hkl) tertentu kadang intensitas berkas
terdifraksi menjadi nol. Hal ini terjadi karena faktor struktur geometri Fhkl=0,
meskipun bidang (hkl) yang bersesuaian memenuhi kondisi Bragg.
Misalnya, semua atom identik, kedudukan atom ke-j dalam sel satuan
δ j = u j a + v jb + w jc
dan kondisi Bragg terpenuhi
s = Ghkl = ha ∗ + kb ∗ + lc ∗

maka
( )
Fhkl = f a ∑ e
2πi hu j + kv j + lw j
(1.32)
j

Contoh menghitung faktor struktur geometri Fhkl.
a. Sel satuan primitip (P). Atomnya terletak di 000 sehingga (1.32) menjadi
Fhkl = fa
b. Sel satuan “base centered” C. Atomnya terletak di 000 dan ½½0 sehingga
(1.32) menjadi
Fhkl = fa (1 + eπi(h + k))
Dengan demikian Fhkl≠0 hanya jika h+k=2n dengan n=0, ±1, ±2, …
c. Sel satuan “body centered” I. Atomnya terletak di 000 dan ½½½ sehingga
(1.32) menjadi
Fhkl = fa (1 + eπi(h + k+ l))
Dengan demikian Fhkl≠0 hanya jika h+k+l=2n dengan n=0, ±1, ±2, …
d. Sel satuan “face centered” F. Atomnya terletak di 000, ½½0, ½0½ dan 0½½
sehingga (1.32) menjadi
Fhkl = fa (1 + eπi(h + k) + eπi(h + l) + eπi(k + l))
Dengan demikian Fhkl≠0 hanya jika h+k=2n dan k+l=2n dengan n=0, ±1, ±2,
… Dengan kata lain Fhkl≠0 hanya jika semua indek genap atau semua indek
ganjil.



Berikut ini diberikan contoh kurva intensitas refleksi sinar-X dan sudut
hamburan (I vs 2θ) hasil eksperimen difraksi sinar-X dari bubukan KCl dan KBr.

Gambar 1.23 Perbandingan refleksi sinar-X antara bubukan KCl dan KBr
KCl dan KBr, keduanya, memiliki struktur FCC. Dalam KCl, jumlah elektron
pada K+ dan Cl- sama banyak sehingga faktor hamburan atom fa keduanya hampir
sama sehingga ia “terlihat” oleh sinar-X sebagai kristal SC monoatomik dengan
konstanta kisi a/2. Adanya refleksi indek-indek yang genap bulat menunjukkan
bahwa kristal tersebut adalah SC dengan konstanta kisi a. Sedangkan dalam KBr,



faktor hamburan atomnya berbeda sehingga ia tetap terlihat sebagai struktur FCC
oleh difraksi sinar-X.
Kondisi Bragg (1.27) masih dapat ditulis dalam bentuk lain. Substitusi
(1.12) ke dalam (1.27) menghasilkan
k − ko = G (1.33)
Mengalikan kedua ruas (1.33) dengan ħ menghasilkan
ko = k − G

Persamaan ini dapat dipandang sebagai kekekalan momentum, dan difraksinya
sebagai proses tumbukan antara foton sinar-X dan kristal. Momentum sebelum
tumbukan hanya momentum linier foton yang datang p o = k o , dan setelah

tumbukan adalah momentum linier foton terhambur p = k dan momentum linier

kristal − G . Dengan demikian perubahan momentum linier foton
Δp = p − p o = G

Energi kinetik seluruh kristal Ek=(ħGhkl)2/2M, dengan M adalah massa seluruh
kristal. Karena M sangat besar relatif terhadap massa atom, maka Ek sangat kecil
dan diabaikan. Dengan demikian dalam proses hamburan foton sinar-X tidak ada
energi yang hilang

Eo = E → c ko = c k → ko = k

Jelaslah bahwa proses hamburan tersebut di atas bersifat elastik.

1.3 IKATAN ATOMIK DALAM KRISTAL

1.3.1 Gaya Antaratom
Dalam suatu kristal letak atom relatif jauh satu sama lain sehingga gaya
inti tidak berperan. Dengan demikian formasi kristal terjadi karena gaya
antaratom. Dalam kristal, gaya antaratom bersifat listrik.
Energi kristal lebih rendah daripada energi atom bebasnya. Hal ini
menyebabkan kristal lebih stabil daripada atom-atom bebas penyusunnya.
Misalnya, kristal NaCl lebih stabil daripada kumpulan atom-atom Na dan Cl
bebas. Perbedaan energi ini, disebut energi ikat (energi kohesi), besarnya sama



dengan energi yang diperlukan untuk memecah kristal tersebut menjadi atom
bebas bagiannya. Energi kohesi berkisar antara 0,02 eV peratom untuk ikatan
terlemah (ikatan Van der Walls) dan 10 eV peratom untuk ikatan terkuat (ikatan
kovalen). Ikatan logam terletak di antara dua harga ekstrim tersebut.
Molekul adalah sekelompok atom bermuatan listrik netral, terikat kuat
bersama dan berperilaku sebagai partikel tunggal. Suatu jenis molekul tertentu
memiliki komposisi dan struktur tertentu pula. Energi potensial yang
merepresentasikan interaksi antara dua atom dalam suatu molekul sebagai fungsi
jarak diperlihatkan pada Gambar 1.24 berikut.

Gambar 1.24 Energi potensial sebagai fungsi jarak dari ikatan dua atom
Posisi setimbang ditandai oleh energi terendah –Vo, yang terjadi pada jarak Ro
yang berordo beberapa angstrom. Pada R>Ro, potensial naik secara bertahap
sehingga mencapai nol pada R→∞ (dua atom bebas). Sedangkan pada R<Ro,
potensial naik secara tajam menuju ∞.
Gaya antaratom dapat dirumuskan
F (R ) = −∇V (R ) (1.34)
Terlihat bahwa F(R)<0 untuk R>Ro, sehingga terjadi tarik-menarik; dan F(R)>0
untuk R<Ro, sehingga terjadi tolak-menolak antara dua atom tesebut. Kedua gaya
ini saling meniadakan satu sama lain pada titik setimbang Ro. Tetapi, umumnya,
energi tarikan mendominansi energi tolakan pada titik setimbang Ro.



1.3.2 Jenis Ikatan Kristal

1.3.2.1 Ikatan Ionik
Ikatan ini terjadi antara ion positip dan negatip sehingga sering disebut
ikatan heteropolar. Setelah terjadi perpindahan elektron, konfigurasi elektron ion
menyerupai gas mulia. Oleh karena itu sebaran muatan elektronnya mempunyai
simetri bola. Contohnya adalah ikatan yang terjadi pada alkalihalida.
Biasanya, ikatan ionik tidak menghasilkan pembentukan molekul yang
berpasangan, tetapi merupakan kumpulan ion positip dan negatip yang tersusun
dalam struktur tertentu. Misalnya, struktur FCC NaCl, dalam setiap bentuk dan
ukuran apapun selalu berisikan jumlah ion Na+ dan ion Cl- yang sama banyak.
Apabila Uij adalah energi interaksi antara ion ke-i dan ke-j, maka energi
total ion ke-i adalah
U i = ∑ U ij (1.35)
j

dimana penjumlahan dilakukan untuk semua ion kecuali j=i. Energi Uij berasal
dari potensial tolak-menolak medan sentral empirik λ eksp (-rij/ρ), dimana λ
(tetapan) dan ρ (panjang karakteristik) merupakan parameter empirik; dan tarik-
menarik Coulomb ±q2/4πεorij. Dengan demikian

− rij / ρ q2
U ij = λ e ± (1.36)
4πε o rij

Potensial tolak-menolak terjadi karena penerapan prinsip eksklusi Pauli saat jarak
antarion berkurang (lebih kecil dari jarak kesetimbangan). Berkurangnya jarak
antarion menyebabkab orbit elektron tumpang-tindih. Hal ini melanggar prinsip
eksklusi Pauli karena sel terluar ion sudah komplit. Akibatnya elektron harus
menempati tingkat energi yang lebih tinggi sehingga energi potensial naik secara
tajam. Sedangkan potensial Coulomb terjadi antara ion sejenis (tanda +) atau tidak
sejenis (tanda -).
Energi kisi kristal total yang terdiri dari N buah molekul atau 2N buah ion
Utot = N Ui



Ungkapan ini menunjukkan bahwa setiap pasangan atau setiap ikatan hanya
dihitung sekali. Andaikanlah r kita tulis sebagai rij=pijR, dengan R adalah jarak
terdekat antara dua atom terdekat dan interaksi tolak-menolak hanya terjadi
antartetangga terdekat saja, maka
⎧ q2
⎪ λ e −R / ρ − (te tan gga terdekat )
⎪ 4πε o R
U ij = ⎨ 2 (1.37)
⎪± 1 q (bukan te tan gga terdekat )
⎪ pij 4πε o R
⎩
sehingga energi total
⎛ α q2 ⎞
U tot = NU i = N ⎜ zλ e − R / ρ −
⎜ ⎟ (1.38)
⎝ 4πε o R ⎟
⎠
dengan z = jumlah tetangga terdekat suatu ion
±1
α =∑ adalah konstanta Madelung (termasuk j=i)
j pij

Dalam menghitung konstanta Madelung, jika ion referensi bermuatan negatip,
maka tanda (+) digunakan untuk ion positip dan tanda (-) untuk ion negatip. Jika
dU tot
diambil syarat bahwa = 0 , maka diperoleh
dR R = Ro

ραq 2
Ro2 e − Ro / ρ = (1.39)
4πε o λ z
Dengan menggunakan (1.38) dan (1.39), maka energi kisi kristal total dengan 2N
buah ion pada jarak setimbang Ro
Nαq 2 ⎛ ρ ⎞
U tot =− ⎜1 −
⎜ R ⎟ ⎟ (1.40)
R = Ro
4πε o Ro ⎝ o ⎠

Nαq 2
Bentuk − disebut energi Madelung. Harga ρ berorde 0,1Ro sehingga
4πε o Ro

interaksi tolak-menolak mempunyai rentang yang amat pendek dan sedikit sekali
pengaruhnya terhadap energi kisi.
Sebagai contoh disajikan data tentang energi permolekul dalam kristal
KCl, yaitu energi Madelung (energi Coulomb) sebesar (25,2)/R eV dan energi



tolak menolak (2,4.104)exp(-R/0,30) eV dimana R berorde 10-8 cm. Harga
konstanta Madelung α bergantung pada struktur kristal ionik, misalnya untuk
NaCl, CsCl dan ZnS, masing-masing berharga 1,747565 , 1,762675 dan 1,6381.
Ikatan ionik tergolong lebih kuat daripada ikatan lain, dengan energi rata-
rata 5 eV setiap pasangan atom. Oleh karena itu kristal ionik mempunyai titik
leleh yang tinggi. Misalnya titik leleh NaCl adalah 8010C, sedangkan untuk logam
Na dan K, masing-masing adalah 97,80C dan 630C.

1.3.2.2 Ikatan Kovalen
Andaikanlah ada dua atom hidrogen yang terpisah pada jarak yang cukup
jauh satu sala lainnya sehingga tidak ada interaksi di antara elektronnya, maka
masing-masing atom memiliki orbit 1s. Jika kedua atom saling mendekat dan
membentuk molekul H2, maka orbital molekulnya merupakan kombinasi linier
dari kedua orbital atom 1s. Orbital molekul tersebut mempunyai dua
kemungkinan, yaitu
ψ genap = ψ 1 + ψ 2 dan ψ ganjil = ψ 1 − ψ 2 (1.41)

dimana ψ1 dan ψ2 merepresentasikan keadaan 1s pada dua proton. Orbital
molekular ψgenap dan ψganjil secara grafik diperlihatkan pada Gambar 1.25 berikut.

a b

Gambar 1.25 Fungsi gelombang (a) ψgenap dan (b) ψganjil

Sedangkan distribusi muatan untuk kedua orbital tersebut adalah |ψgenap|2 dan
|ψganjil|2 seperti ditunjukkan oleh Gambar 1.26 berikut.

(a) (b)
Gambar 1.26 Propil distribusi muatan dan representasi kontur



(a) ψgenap dan (b) ψganjil

Tampak bahwa ψgenap mengandung elektron terutama pada daerah antara dua
proton, sedangkan ψganjil mengandung elektron di sekitar masing-masing proton
yang bersangkutan dan jauh dari daerah antara dua proton.
Kedua orbital molekul di atas mempunyai energi yang berbeda seperti
ditunjukkan oleh Gambar 1.27 berikut.

Gambar 1.27 Energi keadaan dasar dan eksitasi molekul hidrogen
sebagai fungsi jarak antarinti
Orbital genap berenergi lebih rendah daripada orbital ganjil. Bahkan orbital genap
mempunyai energi negatip. Dengan demikian orbital genap merupakan orbital
stabil (orbital bonding) dan orbital ganjil merupakan orbital tidak stabil (orbital
antibonding). Pada gambar di atas tampak bahwa molekul hidrogen memiliki
keadaan setimbang pada 0,74 Å dan energi ikat 4,48 eV (relatif terhadap keadaan
dasar dua atom hidrogen yang terpisah pada jarak tak terhingga). Sesuai dengan
prinsip eksklusi Pauli, kedua elektron dalam orbital bonding memiliki spin
antiparalel.
Keberadaan sepasang elektron di antara atom hidrogen di atas
menyebabkan terjadinya ikatan yang kuat dalam molekul hidrogen. Ikatan yang
terjadi karena pemakaian bersama sepasang elektron oleh atom untuk mencapai
konfigurasi gas mulia dalam suatu molekul disebut ikatan kovalen. Hal ini



merupakan bukti bahwa semua atom adalah identik sehingga transfer elektron dari
satu atom ke yang lain tidak menimbulkan akibat apapun.
Keadaan fisis ikatan kovalen dalam kristal sama dengan dalam molekul.
Gaya tarikan terjadi antara elektron dan proton di sepanjang garis yang
menghubungkan inti berturutan. Sedangkan gaya tolaknya terjadi karena interaksi
prinsip eksklusi Pauli saat inti saling merapat. Gaya tarikan elektron-proton lebih
dari cukup untuk mengimbangi penolakan langsung elektron-elektron ataupun
proton-proton.
Ikatan kovalen juga kuat, seperti ditunjukkan oleh intan yang tingkat
kekerasannya tinggi dan titik leleh di atas 30000C. Ikatan dua atom karbon dalam
struktur intan memiliki energi kohesi 7,3 eV peratom.

1.3.2.3 Ikatan Logam
Model ikatan logam menggambarkan adanya suatu susunan ion teratur dan
suatu lautan elektron valensi ion tersebut yang dapat bergerak bebas di antara
susunan ion. Dengan demikian elektron valensi atom berubah menjadi elektron
konduksi logam. Ikatan logam terjadi bila tarikan antara ion positip dan gas
elektron melebihi penolakan antarelektron dalam gas tersebut. Gaya tolak
Coulomb antarion positip menjadi tidak efektif karena gas elektron melingkupi
ion secara kuat sehingga menjadi ion noninteraksi yang netral.
Atom logam bersatu sehingga terbentuk kristal logam yang stabil karena
energi sistem kristal lebih rendah daripada energi atom bebasnya. Dalam atom
bebas terisolasi, elektron dimodelkan sebagai sebuah partikel dalam kotak
potensial. Dengan demikian gerakan elektron dibatasi dalam volume yang kecil
sehingga, menurut prinsip ketidaktentuan Heisenberg, energi kinetiknya besar.
Dengan menggunakan persamaan Scrodinger, dimana potensial interaksi nol, dan
syarat batas periodik diperoleh energi kinetik elektron
E ∼ V-2/3 (1.42)
Dimana V adalah volume kotak tempat elektron bergerak. Sedangkan dalam
kristal, elektron secara bebas bergerak dalam keseluruhan volume kristal yang
sangat besar. Akibatnya, energi kinetik elektron turun secara tajam dan



mengkontribusi pengurangan energi total sistem. Penurunan energi inilah yang
menjadi sumber ikatan logam.
Ikatan logam lebih lemah daripada ikatan kovalen dan ionik. Contohnya,
logam Na memiliki titik leleh pada 97,80C. Energi kinetik yang kecil
menyebabkan ikatannya lemah. Susunan kristal logam cenderung untuk memiliki
susunan dimana setiap atom atau ion memiliki banyak tetangga (struktur tersusun
padat), misalnya HCP (seng), FCC (tembaga), BCC (lithium dan natrium) dan
lain-lain.

1.3.2.4 Ikatan Van der Walls
Ikatan ionik, kovalen dan logam terjadi karena pengaturan elektron
valensi. Hal demikian tidak bisa terjadi pada gas mulia yang sangat stabil karena
sel terluarnya penuh. Distribusi elektronnya mempunyai simetri bola sehingga
potensial listrik berharga nol di luar jari-jari atom. Demikian juga momen
multipol listriknya. Jika hal ini benar, maka atom gas mulia tidak memiliki energi
kohesi dan tidak dapat terkondensasi menjadi cairan. Tetapi, terjadinya
kondensasi dan pembekuan pada suhu yang sangat rendah membuktikan bahwa
terdapat energi ikat yang lemah pada gas ini. Gaya yang lemah antaratom dalam
padatan gas mulia ditandai oleh titik lelehnya yang rendah, yaitu -272,20C, -
248,70C dan -189,20C, masing-masing untuk He, Ne dan Ar.
Meskipun secara rata-rata semua momen multipol listriknya sama dengan
nol, tetapi di setiap suatu waktu momen dipol listrik tidak sama dengan nol
sebagai akibat adanya kelebihan elektron di bagian tertentu. Ketidaksimetrisan ini
tidak permanen, tetapi selalu berfluktuasi. Momen dipol listrik sesaat ini dapat
menginduksi atom atau molekul tetangganya sehingga terjadi interaksi antara
keduanya. Interaksi antara momen dipol listrik sesaat inilah yang memberikan
ikatan antara atom gas mulia.
Interaksi tarik-menarik dipol induksi antara dua dipol berjarak R telah
dirumuskan oleh Van der Walls – London melalui energi
A
ΔU = − (1.43)
R6



Interaksi tolak-menolaknya bersumber dari interaksi prinsip eksklusi Pauli. Secara
empirik didapatkan potensial tolak-menolak
B
ΔU = (1.44)
R 12
A dan B adalah parameter empirik. Sehingga, biasanya, energi potensial total dua
atom berjarak R adalah
⎡⎛ σ ⎞12 ⎛ σ ⎞ 6 ⎤
U (R ) = 4ε ⎢⎜ ⎟ − ⎜ ⎟ ⎥ (1.45)
⎢⎝ R ⎠
⎣ ⎝R⎠ ⎥ ⎦
dimana ε dan σ adalah parameter baru, dengan 4εσ6=A dan 4εσ12=B. Potensial
(1.45) di atas dikenal dengan nama potensial Lennard-Jones.
Gaya antara dua atom ditentukan melalui –dU/dR. gaya ini sangat cepat
berubah dengan jarak R sehingga atom dalam kristal cenderung untuk serapat
mungkin. Biasanya, struktur yang dimiliki oleh gas mulia adalah FCC (“cubic
close-packed”).
Energi kinetik atom gas mulia dapat diabaikan. Oleh karena itu energi
kohesi kristal gas mulia didapatkan dengan menjumlahkan potensial Lennard-
Jones (1.45) di atas terhadap semua pasangan atom dalam kristal. Jika terdapat N
buah atom dalam kristal, maka energi tersebut
⎡ ⎛ σ ⎞12 ⎛ σ ⎞ ⎤
6

U tot = N (4ε )⎢∑ ⎜
1 ⎟ − ∑⎜ ⎟ ⎥ (1.46)
⎢ j ⎜ pij R ⎟ ⎜ p R⎟ ⎥
2
⎣ ⎝ ⎠ ⎝ ij ⎠ ⎦

dimana pijR adalah jarak antara atom ke-i dan j. Faktor ½ muncul karena hitungan
dilakukan dua kali pada setiap pasangan atom.
Untuk struktur FCC, dimana terdapat 12 tetangga terdekat, perhitungan
menghasilkan

∑pj
−12
ij = 12,13188 ; ∑p
j
−6
ij = 14,45392 (1.47)

Pada posisi setimbang Ro, energi total sistem berharga minimum sehingga
dU tot ⎡ σ 12 σ6⎤
= 0 = −2 Nε ⎢(12 )(12,13) 13 − (6)(14,45) 7 ⎥ (1.48)
dR R = Ro ⎣ R R ⎦

dan menghasilkan harga



Ro/σ = 1,09 (1.49)
Nilai Ro/σ hasil pengamatan menunjukkan untuk Ne, Ar, Kr dan Xe adalah 1,14;
1,11; 1,1 dan 1,09 yang tidak berbeda jauh dengan (1.49). Dengan demikian
energi kohesi kristal gas mulia pada suhu nol mutlak dan tekanan nol diperoleh
dengan mensubstitusikan (1.47) dan (1.49) ke dalam (1.46). Hasilnya diperoleh
⎡ ⎛σ ⎞
12
⎛σ ⎞ ⎤
6

U tot (R ) = 2 Nε ⎢(12,13)⎜ ⎟ − (14,45)⎜ ⎟ ⎥ (1.50)
⎢
⎣ ⎝R⎠ ⎝R⎠ ⎥ ⎦
dan pada posisi setimbang Ro
Utot(Ro) = - (2,15) (4Nε) (1.51)
Perhitungan energi kohesi ini berlaku jika atom-atom dalam keadaan diam. Jika
dilakukan koreksi mekanika kuantum, maka energi tersebut harus direduksi
sebesar 28; 10; 6 dan 4 %, masing-masing untuk Ne, Ar, Kr dan Xe.

1.3.2.5 Ikatan Hidrogen
Molekul air (H2O) terisolasi berikatan kovalen sehingga atom
penyusunnya terikat secara kuat. Tetapi, dalam kristal es, yang tersusun atas
molekul air, ikatannya jauh lebih lemah. Hal ini ditandai oleh adanya titik leleh air
pada 00C.
Sifat listrik sebuah molekul air terisolasi adalah netral. Tetapi, dalam
kristal es distribusi muatan internal sedemikian rupa sehingga menghasilkan
interaksi antarmolekul. Elektron lebih ditarik ke arah atom oksigen sehingga
bermuatan negatip; dan dalam waktu bersamaan atom hidrogen menjadi
bermuatan positip. Keadaan ini menghasilkan dipol listrik dalam molekul air.
Gaya tarik-menarik antardipol listrik inilah yang menghasilkan ikatan hidrogen
sehingga terbentuk kristal. Hal ini dijelaskan dalam Gambar 1.28 berikut.



Gambar 1.28 (a) Molekul air; dan (b) Susunan molekul air
sebagai akibat adanya ikatan hidrogen
Tetapi, gaya antarmolekul ini jauh lebih lemah daripada gaya internal yang
mengikat molekul itu sehingga molekul tetap dapat mempertahankan identitasnya
salam kristal. Ikatan hidrogen mempunyai orde 0,1 eV.

RINGKASAN
01. Suatu benda padat berbentuk kristal, apabila atom, ion, atau molekulnya
teratur dan periodik dalam rentang yang panjang dalam ruang. Bahan kristal
memiliki simetri translasi, artinya bila seluruh kristal itu digeser sejauh vektor
translasi kisi R = n1 a + n2 b , maka keadaannya tetap sama.
02. Pola geometrik dari kedudukan setimbang tiap atom sebagai suatu titik
dinamakan kisi kristal. Terdapat dua kelas kisi, yaitu Bravais dan non-
Bravais. Kisi non-Bravais seringkali disebut sebagai kisi dengan suatu basis
dan dapat dipandang sebagai kombinasi dari dua atau lebih kisi Bravais yang
saling menembus dengan orientasi tertentu.
03. Luas daerah jajaran genjang yang sisinya dibatasi oleh vektor basis disebut sel
satuan. Terdapat dua jenis sel satuan, yaitu sel primitip (satu titik kisi
perselnya) dan sel non-primitip (lebih dari satu titik kisi perselnya). Hubungan
antara keduanya adalah (a) sel non-primitip menunjukkan simetri lebih besar,
dan (b) luas sel non-primitip merupakan kelipatan bulat dari luas sel primitip.
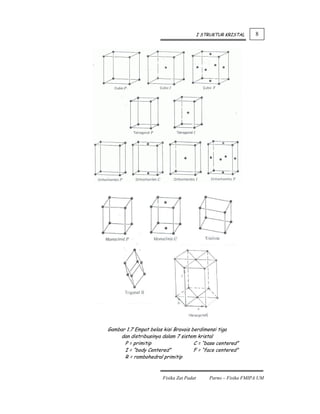
04. Dalam dua dimensi, kisi kristal Bravais yang mungkin sebanyak lima jenis,
yaitu Genjang, Persegi, Heksagonal, Empat persegi panjang P, dan Empat
persegi panjang I. Sedangkan untuk tiga dimensi ternyata ada 14 buah kisi
Bravais yang terlingkupi dalam 7 buah sistem kristal, yaitu Triklinik (P),
Monoklinik (P, C), Ortorombik (P, C, I, F), Tetragonal (P, I), Trigonal (R),
Heksagonal (P), dan Kubik (P, I, F).
05. Beberapa kristal dengan struktur sederhana, di antaranya NaCl, CsCl, intan,
ZnS dan HCP
06. Arah kristal, yakni vektor R = n1 a + n 2 b + n3 c , dinyatakan dengan [n1 n2

n3], yang lazimnya dalam perbandingan bilangan bulat terkecil. Sedangkan



bidang kristal dinyatakan sebagai indek Miller (hkl). Jarak antarbidang Miller,
khusus untuk sumbu ortogonal dengan a≠b≠c dinyatakan oleh persamaan
1
d hkl = 1/ 2
⎛ 1 1 1 ⎞
⎜ 2 + 2 + 2⎟
⎜x
⎝ y z ⎟⎠
07. Fraksi kepadatan, didefinisikan sebagai proporsi maksimum dari volume yang
ada yang dapat diisi oleh bola atom dalam sebuah sel satuan, diungkapkan
dalam bentuk rumusan

F=N
(4 / 3)π r3
V
08. Menurut Bragg kristal direpresentasikan oleh kumpulan bidang paralel yang
bersesuaian dengan bidang atom, yang berperan sebagai cermin. Interferensi
maksimum (konstruktif) yang terjadi memenuhi hukum Bragg
n λ = 2 dhkl sin θ
Dengan menggunakan hukum Bragg, secara eksperimen, jarak antarbidang
dhkl dapat dihitung.
09. Fakta menunjukkan bahwa hamburan berkas sinar-X disebabkan oleh atom
diskrit kristal yang bersangkutan. Oleh karena itu bahasan berikut menelaah
hukum Bragg melalui proses hamburan elastik (hamburan Thomson) sinar-X
oleh elektron dalam setiap atom dalam kristal. Dalam teori ini ditemukan
bahwa intensitas parsial gelombang terhambur sebanding dengan kuadrat
faktor hamburan kristal, yaitu Fkr = F S, dimana S dan F, masing-masing
adalah faktor struktur geometri dan kisi.
10. Faktor struktur kisi S berharga tidak nol, yakni S=N, hanya untuk s = Ghkl ,

yakni vektor hamburan sama dengan vektor kisi resiprok (syarat Bragg). Dari
hubungan ini dapatlah diturunkan hukum Bragg 2dhklsin θ = λ.
11. Jika syarat Bragg terpenuhi dan semua atom identik, maka untuk kedudukan
atom ke-j dalam sel satuan δ j = u j a + v j b + w j c , didapatkan faktor struktur
( )
kisi Fhkl = f a ∑ e
2πi hu j + kv j + lw j
.
j



12. Dalam suatu kristal letak atom relatif jauh satu sama lain sehingga gaya inti
tidak berperan. Dengan demikian formasi kristal terjadi karena gaya
antaratom (bersifat listrik). Pada titik setimbang, energi potensial terendah dan
didominansi oleh energi tarik-menarik, serta resultan gaya nol. Pada jarak lebih
kecil dari titik setimbang, potensial naik secara tajam menuju tak berhingga
dan terjadi gaya tolak-menolak; sedangkan pada jarak yang lebih besar,
potensial naik secara bertahap sehingga mencapai nol pada jarak tak berhingga
dan terjadi gaya tarik-menarik.
13. Ikatan ion terjadi antara ion positip dan negatip karena terjadi perpindahan
elektron sehingga menyerupai kofigurasi gas mulia. Energi ikatan berasal dari
potensial tolak-menolak medan sentral empirik dan tarik-menarik Coulomb. Di

Nαq 2 ⎛ ρ ⎞
titik setimbang energi tersebut adalah U tot =− ⎜ R ⎟
⎜1 − ⎟
R = Ro
4πε o Ro ⎝ o ⎠

14. Ikatan yang terjadi karena pemakaian bersama sepasang elektron oleh atom
untuk mencapai konfigurasi gas mulia dalam suatu molekul disebut ikatan
kovalen. Sepasang elektron tersebut lebih banyak terdistribusi di antara inti-
inti. Gaya tarikan terjadi antara elektron dan proton di sepanjang garis yang
menghubungkan inti berturutan. Sedangkan gaya tolaknya terjadi karena
interaksi prinsip eksklusi Pauli saat inti saling merapat. Gaya tarikan elektron-
proton lebih dari cukup untuk mengimbangi penolakan langsung elektron-
elektron ataupun proton-proton.
15. Model ikatan logam menggambarkan adanya suatu susunan ion teratur dan
suatu lautan elektron valensi (elektron konduksi) ion tersebut yang dapat
bergerak bebas di antara susunan ion. Ikatan logam terjadi bila tarikan antara
ion positip dan gas elektron melebihi penolakan antarelektron dalam gas
tersebut. Gaya tolak Coulomb antarion positip menjadi tidak efektif karena gas
elektron melingkupi ion secara kuat sehingga menjadi ion noninteraksi yang
netral.
16. Terdapat energi ikat yang lemah pada gas mulia. Meskipun secara rata-rata
semua momen multipol listriknya sama dengan nol, tetapi di setiap suatu waktu
momen dipol listrik terjadi secara fluktuatif sebagai akibat adanya kelebihan



elektron di bagian tertentu. Momen dipol listrik sesaat ini dapat menginduksi
atom atau molekul tetangganya sehingga terjadi interaksi antara keduanya.
Interaksi antara momen dipol listrik sesaat inilah yang memberikan ikatan
antara atom gas mulia. Energi ikatan Van der Walls ini adalah
⎡ ⎛ σ ⎞12 ⎛ σ ⎞ ⎤
6

U tot = 1 N (4ε )⎢∑ ⎜ ⎟ − ∑⎜ ⎟ ⎥
⎢ j ⎜ pij R ⎟ ⎜ p R⎟ ⎥
2
⎣ ⎝ ⎠ ⎝ ij ⎠ ⎦

17. Contoh ikatan hidrogen adalah kristal air. Sifat listrik sebuah molekul air
terisolasi adalah netral. Tetapi, dalam kristal es distribusi muatan internal
sedemikian rupa sehingga menghasilkan interaksi antarmolekul. Elektron lebih
ditarik ke arah atom oksigen sehingga bermuatan negatip; dan dalam waktu
bersamaan atom hidrogen menjadi bermuatan positip. Keadaan ini
menghasilkan dipol listrik dalam molekul air. Gaya tarik-menarik antardipol
listrik inilah yang menghasilkan ikatan hidrogen sehingga terbentuk kristal.

LATIHAN SOAL BAB I
ˆ j ˆ
01. Diketahui vektor basis primitip suatu kisi adalah a = ai , b = bˆ, c = ck ,
ˆ
dengan i , ˆ dan k adalah tiga vektor satuan dalam koordinat Kartesian.
ˆ j

a. Gambarlah kisi tersebut!
b. Membentuk kisi Bravais jenis apakan vektor basis tersebut?
c. Berapakah volume sel satuan primitip tersebut?
02.a. Sama dengan soal 01), tetapi untuk vektor basis primitip
j ˆ ˆ ˆ
a = (a / 2)(i + ˆ), b = (a / 2)( ˆ + k ) dan c = (a / 2)(k + i ) !
ˆ j

ˆ
b. Buktikan bahwa ungkapan vektor satuan i , ˆ dan k sebagai kombinasi linier
ˆ j

dari vektor basis primitip ialah
ˆ j ˆ
ai = a − b + c , aˆ = a + b − c dan ak = −a + b + c
ˆ j ˆ ˆ ˆ j ˆ
c. Posisi kedelapan pojok sel adalah 0, a i , a ˆ , a k , a( i + ˆ ), a( i + k ), a( ˆ + k )
ˆ j

ˆ j ˆ
dan a( i + ˆ + k ). Nyatakan posisi-posisi tersebut dalam a , b dan c !



ˆ ˆ
d. Sama dengan (c), tetapi untuk 6 titik pada pusat muka, yaitu (½)a( i + k ),

j ˆ j ˆ ˆ j ˆ
(½)a( ˆ + k ), (½)a( i + ˆ ), (½)a( i + 2 ˆ + k ), (½)a( 2i + ˆ + k ), dan
ˆ j ˆ

ˆ
(½)a( i + ˆ + 2k ) ! (Nyatalah bahwa, berdasarkan (c) dan (d) semua posisi
ˆ j

atom dapat dinyatakan sebagai kombinasi linier dari vektor kisi primitip
dengan koefisien bilangan bulat)
03.a. Sama dengan soal 02), tetapi untuk vektor basis primitip
ˆ j ˆ j ˆ ˆ ˆ ˆ j
a = (a / 2)(i + ˆ − k ), b = ( a / 2)( ˆ + k − i ) dan c = (a / 2)(k + i − ˆ) !
ˆ
b. Buktikan bahwa ungkapan vektor satuan i , ˆ dan k sebagai kombinasi linier
ˆ j

ˆ j ˆ
dari vektor basis primitip adalah ai = a + c , aˆ = a + b dan ak = b + c !

04. Sama dengan soal (1), tetapi untuk vektor basis primitip 1 ˆ j ˆ
a (i + ˆ ) − 1 ck ,
2 2

1 ˆ
a (−i + ˆ) + 1 ck , dan
ˆ j 1 ˆ
a (i − ˆ) + 1 ck dimana a adalah sisi bujursangkar dan
ˆ j
2 2 2 2

c adalah sisi yang tegak lurus terhadap bujursangkar tersebut !
05. Kisi kristal dapat dipetakan ke dalam dirinya sendiri oleh simetri translasi kisi,
pencerminan dan rotasi di sekitar suatu sumbu. Kisi kristal memiliki simetri
rotasi derajat-1, 2, 3, 4 dan 6 atau 2π; 2π/2; 2π/3; 2π/4; dan 2π/6. Tetapi,
misalnya, kisi kristal tidak memiliki simetri rotasi 2π/5 karena tidak
memungkinkan untuk mengisi seluruh ruang secara periodik dengan bentuk
bangun pentagon. Tunjukkan bahwa kisi dua dimensi tidak mempunyai
simetri putar 2π/5 !

06. Buktikan bahwa struktur HCP memiliki rasio sumbu c/a= 2 6 =1,633 !
3

07. Pada suhu 1190 K besi memiliki struktur FCC dengan parameter kisi a=3,647
Å; dan pada suhu 1670 K berstruktur BCC dengan a=2,932 Å. Jika berat atom
besi adalah 55,85 sma, maka tentukan kerapatan massa pada masing-masing
suhu tersebut!
08. Diketahui padatan Al berstruktur FCC dengan a=4,04 Å dan berat atom 26,98
sma. Hitunglah massa jenisnya!
09. Gambarlah bidang dan arah berikut dalam sel satuan kubik: (122), [122],
(1 1 2) dan [1 1 2]!



10. Kristal Cu mempunyai struktur FCC dengan jari-jari atom 1,278 Å. Berapakah
kerapatan atom yang terdapat pada bidang (100)?
11. Sama dengan soal 08), tetapi untuk kristal Fe yang berstruktur BCC dengan
konstanta kisi 2,86 Å!
12. Buktikan bahwa dalam koordinat Kartesis bidang (hkl)=(mnox+mnoy+mnoz)
memberikan vektor arah yang tegak lurus bidang tersebut, yakni
ˆ j ˆ
no = nox i + noy ˆ + noz k !

13. Buktikan harga jari-jari atom dan fraksi kepadatan dari berbagai struktur
kristal dalam Tabel 5.1!
14. Suatu kristal kubik mempunyai konstanta kisi 2,62 Å. Berapakah sudut Bragg
yang sesuai untuk terjadi refleksi oleh bidang (100), (110), (111), (200), (210)
dan (211), jika berkas sinar-X monokhromatik yang digunakan mempunyai
panjang gelombang 1,54 Å?
15. Sudut Bragg untuk refleksi kristal besi BCC pada bidang (110) adalah 220,
dengan sinar-X yang panjang gelombangnya 1,54 Å.
a. Berapakah konstanta kisinya?
b. Jika berat atom Fe adalah 55,8 sma, maka berapakah kerapatan massanya?
16. Buktikan bahwa persamaan (1.21) dapat diturunkan dari persamaan (1.20),
dengan mengingat definisi (1.22)!
17. Gambarkan kisi resiprok untuk kisi dua dimensi yang mana a=1,25 Å, b=2,50
Å dan γ=120o!

18.a. Buktikan bahwa vektor kisi resiprok G = ha1 + ka 2 + la3 tegak lurus

terhadap bidang (hkl) dalam kisi kristal!
b. Buktikan bahwa jarak antara dua bidang paralel berturutan dalam kisi adalah

dhkl=2π/ G !

19. Suatu sel satuan berukuran a=4 Å, b=6 Å, c=8 Å dan α=β=900, γ=1200.
Tentukan
a. vektor basis a*, b* dan c* untuk kisi resiprok!
b. jarak antar bidang (210)!



c. sudut Bragg untuk bidang (210), jika diketahui panjang gelombang sinar-X
yang dipakai 1,54 Å!
20. Buktikan bahwa
a. kisi resiprok suatu kisi SC adalah kisi SC juga!
b. kisi resiprok suatu kisi FCC adalah kisi BCC, dan sebaliknya!
21. Diketahui bahwa vektor basis primitip kisi ruang heksagonal adalah
a1 = ( 1 a 3 ) x + ( 1 a ) y, a 2 = −( 1 a 3 ) x + ( 1 a ) y, a3 = cz
2
ˆ 2 ˆ 2
ˆ 2 ˆ ˆ

a. Tunjukkan bahwa volume sel primitipnya adalah (31/2/2)a2c!
b. Tunjukkan bahwa vektor basis primitip kisi resiproknya adalah
⎛ 2π ⎞ ⎛ 2π ⎞ ⎛ 2π ⎞ ⎛ 2π ⎞ 2π
b1 = ⎜
⎜ ⎟x + ⎜
⎟ˆ ⎟ y, b2 = −⎜
ˆ ⎜ ⎟ x + ⎜ ⎟ y, b3 =
⎟ˆ ˆ ˆ
z , sehingga kisi
⎝a 3⎠ ⎝ a ⎠ ⎝a 3⎠ ⎝ a ⎠ c
merupakan resiprok dirinya sendiri, tetapi dengan merotasikan 30o sumbu-
sumbunya terhadap sumbu a3!
22. Buktikan persamaan (1.26)!
23.a. Pada bidang yang mana dalam kisi BCC berikut yang tidak menimbulkan
refleksi Bragg: (100), (110), (111), (200), (210) dan (211)!
b. Sama dengan soal a), tetapi dalam kisi FCC!
24. Hitunglah faktor struktur geometri F100 untuk kristal CsCl yang berstruktur
BCC, jika diasumsikan bahwa fCs=3fCl!
25. Teori ikatan kristal ionik model Born-Meyer menyebutkan bahwa energi
A α q2
potensial total suatu sistem kristal ionik adalah E = N −N , dengan
Rn 4π ε 0 R
N adalah jumlah pasangan ion positip-negatip. Suku pertama
merepresentasikan potensial tolak-menolak, dengan A dan n adalah konstanta
yang ditentukan melalui eksperimen. Suku kedua merepresentasikan potensial
tarik-menarik Coulomb, dengan α adalah konstanta Madelung yang hanya
bergantung pada struktur kristal.
4π ε 0 A
a. Tunjukkan bahwa jarak kesetimbangan antarion adalah R0n −1 = n!
α q2
b. Tunjukkan bahwa energi ikatan pada titik kesetimbangan adalah



α Nq 2 ⎛ 1 ⎞
E0 = − ⎜1 − ⎟ !
4π ε 0 R0 ⎝ n ⎠
c. Jika kristal NaCl mempunyai konstanta kisi 5,63 Å, energi ikat terukur 7,95
eV/molekul dan konstanta Madelung 1,75, maka tentukan konstanta n!

26. Berikut disajikan data eksperimen tentang pembentukan molekul NaCl
Na (gas) + 5,14 eV (energi ionisasi) → Na+ (gas) + e- (elektron)
-
e (elektron) + Cl (gas) → Cl- (gas) + 3,61 eV (afinitas elektron)
Na+ (gas) + Cl- (gas) → NaCl (kristal) + 7,9 eV (energi kohesif)
Hitunglah energi permolekul kristal NaCl tersebut! (Energi permolekul ini
lebih kecil daripada energi kohesif/ikat permolekul (7,9 eV). Energi ikat
molekul adalah energi yang diperlukan untuk memecahkan molekul tersebut
menjadi ion-ion penyusunnya)
27. Dalam kristal NaCl didapatkan data eksperimen tentang harga jarak suatu ion
positip terhadap ion negatip terdekatnya adalah 2.81.10-8 cm. Tentukan energi
tarik menarik Coulomb sebagai bagian dari energi potensial antara dua ion
tersebut! (Harga ini masih seorde dengan data eksperimen tentang energi ikat
7,9 eV/molekul)
29. Buktikan bahwa konstanta Madelung
a. berharga 2 ln 2 untuk kristal ionik alternasi satu dimensi!
b. berharga 1,747565 , 1, 762675 dan 1,6381 , masing-masing untuk kristal
NaCl, CsCl dan ZnS!
30. Untuk gas He, yang berstruktur FCC, hasil pengukuran menunjukkan bahwa
parameter Lennard-Jones ε=50.10-16 erg dan σ=2,96 Å. Hitunglah energi
kohesifnya dalam kJ/mol! (Nilai pengamatan energi kohesif 0,751 kJ/mol, jauh
lebih kecil daripada hasil perhitungan sehingga koreksi kuantum sangat
penting)
31. Dengan menggunakan potensial Lennard-Jones, hitunglah perbandingan
energi kohesi Ne dalam struktur BCC dan FCC! Diketahui bahwa untuk kisi
BCC harga ∑p
j
−12
ij = 9,11418 ; ∑p
j
−6
ij = 12,2533 .



32. Sama dengan soal 26), tetapi untuk struktur HCP dan FCC! Diketahui bahwa
untuk kisi HCP harga ∑p
j
−12
ij = 12,13229 ; ∑pj
−6
ij = 14,45489 .

6 12
⎛a ⎞ ⎛a ⎞
33. Energi total untuk 2 atom argon adalah E = −C ⎜ o ⎟ + B⎜ o ⎟ relatif
⎝R⎠ ⎝R⎠
terhadap keadaan keduanya pada jarak tak terhingga. Harga B= 2,35.103 eV,
C= 1,69.108 eV dan ao adalah radius Bohr. Suku pertama merepresentasikan
energi tarik menarik antara elektron-elektron terluar; dan kedua adalah energi
tolak menolak antara ion-ion teras. Hitunglah
a. posisi setimbang !
b. Buktikan bahwa di posisi setimbang energinya didominansi oleh energi
tarik menarik! (harga mutlak energi tarik menarik lebih besar daripada
energi tolak menolak, dan energi totalnya berharga negatip)


B A B II
DINAMIKA KISI KRISTAL

Bahasan struktur kristal pada bab lalu menganggap bahwa atom bersifat
statik pada masing-masing titik kisinya. Sebenarnya, atom tidaklah statik,
melainkan berosilasi di sekitar titik setimbangnya sebagai akibat energi termal.
Bab ini membahas vibrasi kisi secara agak rinci.
Bab ini mula-mula membahas vibrasi kristal dalam batasan panjang
gelombang elastik, yang mana kristal dapat dianggap medium kontinu. Kapasitas
panas bahan dikemukakan dalam beberapa model, dan yang sesuai dengan
eksperimen adalah hanya yang menggunakan konsep fisika kuantum. Akhirnya,
bab ini ditutup oleh bahasan vibrasi kisi kristal, yang dikaitkan dengan sifat diskrit
kisi.

2.1 GETARAN DALAM ZAT PADAT

2.1.1 Getaran Elastik dan Rapat Moda Getar
Padatan terdiri dari atom diskrit. Atom tidaklah diam, tetapi berosilasi di
sekitar titik setimbangnya sebagai akibat adanya energi termal. Namun, saat
gelombang yang merambat mempunyai panjang gelombang yang jauh lebih besar
daripada jarak antaratom, sifat atomik dapat diabaikan dan padatan dapat
dianggap sebagai medium kontinu. Dengan demikian persoalan fisisnya
menyangkut lingkup makro. Gelombang yang demikian disebut gelombang
elastik.
Misalnya, gelombang suara elastik longitudinal merambat dalam suatu
batang isotropik, yang mempunyai penampang A, massa jenis ρ dan modulus
Young Y, antara x dan (x+dx) menurut hukum Newton mempunyai persamaan
gerak

II DINAMIKA KISI KRISTAL 48

∂ 2u
ρ A dx = [S ( x + dx) − S ( x)]A (2.1)
∂t 2
dimana u adalah simpangan terhadap titik setimbang dan S adalah tekanan.
Regangan e=du/dx dan tekanan S dihubungkan oleh hukum Hooke
S=Yu (2.2)
Untuk bagian yang kecil sesungguhnya
ΔS = S(x+dx) – S(x) = (∂S/∂x) dx
sehingga persamaan gerak gelombang (2.1) di atas menjadi
∂ 2u ρ ∂ 2u
− =0 (2.3)
∂x 2 Y ∂t 2
yang dikenal sebagai persamaan gelombang satu dimensi.
Diambil solusi berbentuk propagasi gelombang bidang, yaitu
u = Ao ei(kx - ωt) (2.4)
Dimana Ao, k dan ω adalah amplitudo, bilangan gelombang dan frekuensi radial
gelombang. Substitusi solusi (2.4) ke dalam persamaan gelombang (2.3)
menghasilkan
ω = vs k (2.5)
dengan
vs = (Y/ρ)1/2 (2.6)
adalah kecepatan fasa gelombang. Hubungan (2.5) antara frekuensi dan bilangan
gelombang disebut relasi dispersi. Dalam hal ini hubungan tersebut adalah linier,
dengan kemiringan kecepatan fasa, seperti disajikan pada Gambar 2.1 berikut.

ω

ω=vsk

0 k

Gambar 2.1 Kurva dispersi gelombang elastik



Relasi dispersi linier (dengan kecepatan suara vs sebagai kemiringannya) dimiliki
oleh beberapa gelombang, antara lain gelombang optik dalam vakum, dan
gelombang suara dalam cairan dan gas.

Penyimpangan terhadap sifat linier di atas disebut dispersi. Ketidaklinieran
terjadi karena, khususnya, panjang gelombang yang relatif kecil jika dibandingkan
dengan jarak antar atom. Hal ini akan dipelajari pada getaran dalam kisi kristal.

Persamaan (2.6) dapat digunakan untuk menentukan modulus Young.
Misalnya, pengukuran menunjukkan untuk suatu padatan tertentu vs= 5.105 cm/s
dan ρ = 5 gr/cm3 sehingga didapatkan nilai Y = 1,25.1012 gr/cm s2.

Apabila gelombang elastik satu dimensi di atas hanya diperhatikan solusi
domain ruangnya saja, yakni
u = Ao eikx (2.7)
dan ujung batang sebelah kanan berosilasi sama dengan sebelah kiri sehingga
memiliki syarat batas periodik
u (x=0) = u (x=L) (2.8)
dengan L adalah panjang batang, maka substitusi (2.7) ke dalam (2.8)
menghasilkan kondisi
eikL = 1 (2.9)
sehingga
kn = (2π/L) n, dimana n=0, ±1, ±2, … (2.10)
Setiap nilai n di atas memberikan satu harga k sebagai representasi sebuah moda
getar.
Jika L besar sekali, maka kn hampir kontinu (pandangan makro). Dalam
domain k, jarak antartitik adalah (2π/L), sehingga jumlah moda getar antara k dan
(k+dk) sebesar
dN = (L/2π) dk (2.11)
Dalam domain frekuensi, dN di atas terletak antara ω dan (ω+dω). Rapat keadaan
g(ω) didefinisikan sedemikian sehingga bentuk g(ω)dω memberikan jumlah moda
getar yang mempunyai frekuensi antara ω dan (ω+dω) seperti di atas. Oleh karena
itu didapatkan



L 1
g (ω ) =
2π dω / dk
Ungkapan ini hanya berlaku untuk gerakan dalam satu arah positip saja. Dengan
demikian g(ω) yang mencakup gelombang ke kiri dan ke kanan adalah
L 1
g (ω ) = (2.12)
π dω / dk
Terlihat bahwa rapat keadaan g(ω) bergantung pada relasi dispersi. Untuk
hubungan linier (2.5), dimana dω/dk=vs, maka didapatkan
L 1
g (ω ) = (2.13)
π vs
yang konstan tidak bergantung pada ω.

Bahasan tiga dimensi kubik dengan rusuk L memberikan syarat bahwa
(
i kx L+k y L+kz L) )
e =1
sehingga
(kx , ky , kz) = [ n (2π/L) , m (2π/L) , l (2π/L) ] (2.14)
dimana n, m, l = 0, ±1, ±2, …. Representasi dalam ruang k menunjukkan bahwa
sebuah titik mempunyai volume (2π/L)3 dan merepresentasikan satu moda getar,
seperti Gambar 2.2 berikut.

ky
kontur (ω+dω)
kontur ω

kx

dω
k

Gambar 2.2 Nilai diskrit k untuk gelombang yang merambat tiga dimensi



Semua moda getar dengan k tertentu direpresentasikan oleh satu titik yang terletak
pada permukaan bola dalam ruang k, dengan jari-jari k dan berpusat di (kx , ky ,
kz) = (0,0,0).
Semua moda getar dengan vektor gelombang antara k dan (k+dk) terletak
dalam elemen volume 4πk2dk yang dibataskan oleh bola berjari-jari k dan (k+dk).
Dengan demikian, jumlah moda getar dalam selang vektor gelombang di atas
4πk 2 dk k2
dN = =V dk (2.15)
(2π / L )3 2π 2

dimana V=L3 adalah volume sampel. Rapat keadaan g(ω) diperoleh dengan
menggunakan hubungan dispersi ω(k).
Apabila digunakan hubungan dispersi linier (2.5), maka didapatkan
V ω2
g (ω ) = (2.16)
2π 2 v s3
yang dilukiskan dalam Gambar 2.3 berikut.

Gambar 2.3 Rapat keadaan dalam medium elastik

Ternyata bahwa bertambahnya g(ω) berbanding lurus dengan ω2, tidak seperti
dalam kasus satu dimensi dimana g(ω) berharga konstan. Hal ini terjadi karena
kenaikan elemen volume permukaan bola yang berbanding lurus dengan k2; dan
karena itu berbanding lurus juga dengan ω2 karena ω sebanding dengan k.
Ungkapan g(ω) di atas bersesuaian dengan moda tunggal untuk setiap nilai
k . Sebenarnya, dalam tiga dimensi untuk setiap nilai k mengandung tiga moda



berbeda, yaitu satu moda longitudinal dan dua moda transversal. Hubungan
dispersinya juga berbeda. Dengan demikian rapat keadaan (2.16) menjadi

ω2 ⎛ 1 1 ⎞
g (ω ) = V ⎜ 3 + 3⎟
⎜v ⎟ (2.17)
2π 2 ⎝ L vT ⎠
dimana vL dan vT, masing-masing merupakan kecepatan gelombang longitudinal
dan transversal. Jika vL=vT, maka ungkapan (2.17) menjadi
3V ω 2
g (ω ) = (2.18)
2π 2 v s3

2.1.2 Kuantisasi Energi Getaran dalam Zat Padat
Teori klasik kinetik gas menganggap bahwa energi dalam untuk suatu gas
tersimpan sebagai energi kinetik atom tersebut. Hukum ekipartisi menyatakan
bahwa besaran fisis energi yang besarnya berbanding lurus dengan kuadrat jarak
atau momentum, maka untuk setiap derajat kebebasan pada suhu T memiliki
energi sama, yaitu (½)k0T, dengan k0 adalah konstanta Boltzmann. Hal ini berarti
energi kinetik setiap atom gas memiliki energi (½)k0T. Gas monoatomik memiliki
tiga derajat kebebasan, sehingga pada suhu T energi dalam untuk gas sebanyak 1
kilomol
U = NA (3/2) k0T = (3/2) RT (2.19)
Dengan demikian, kapasitas panas pada volume konstan
⎛ ∂U ⎞ 3
CV = ⎜ ⎟ = R (2.20)
⎝ ∂T ⎠V 2
Sesungguhnya, kapasitas panas permol didefinisikan sebagai panas ΔQ yang
diperlukan tiap satu mol untuk menaikkan suhu ΔT, yakni C=ΔQ/ΔT. Jika proses
berlangsung pada volume tetap, maka ΔQ=ΔU, dimana ΔU adalah kenaikan
energi dalam sistem. Dalam hal persamaan di atas, NA adalah bilangan Avogadro
dan R adalah tetapan gas. Menurut (2.20) teori ini menghasilkan nilai CV=12,47
J/0K kmol. Harga ini sesuai untuk gas He dan Ar pada suhu kamar.
Setiap atom dalam kristal, disamping memiliki 3 derajat kebebasan untuk
geraknya di sekitar kedudukan setimbangnya (energi kinetik), juga memiliki
energi potensial atom dalam gerak harmoniknya. Pada gerak selaras sederhana,



energi kinetik rata-rata sama dengan energi potensial rata-rata, sehingga energi
total sistem atom dalam kristal menurut hukum ekipartisi
⎛3 3 ⎞
U = N A ⎜ k oT + k oT ⎟ = 3RT (2.21)
⎝ 2 2 ⎠
Ungkapan ini menunjukkan bahwa kapasitas panas kristal pada volume konstan
adalah
CV = (∂U/∂T)V = 3R (2.22)
Harga (2.22) sesuai dengan penemuan empirik Dulong-Petit (1819), yang berlaku
untuk hampir semua zat padat pada suhu ruang atau yang lebih tinggi.
Selanjutnya, eksperimen menunjukkan bahwa nilai CV menurun apabila T
menurun, dan mendekati nol apabila T menuju 0 K. Disamping itu, terdapat
indikasi yang sangat kuat bahwa pada suhu yang sangat rendah mendekati nol
mutlak
CV ∼ T3
Penyempurnaan bahasan kapasitas panas ini, selanjutnya menggunakan teori
mekanika kuantum.
2.1.2.1 Model Einstein tentang CV Zat Padat
Diilhami oleh keberhasilan Planck dalam menerangkan radiasi benda
hitam, maka konsep kuantisasi energi itu juga diterapkan Einstein dalam teorinya
tentang CV zat padat. Model Einstein tentang getaran kisi mengambil andaian
sebagai berikut.
a. Atom kristal merupakan osilator independen, yang masing-masing memiliki
frekuensi sama dan energi diskrit
εn = n ћ ω , n = 0, 1, 2, … (2.23)
dengan ω adalah frekuensi osilator. Jarak antartingkat energi ini sebesar ћ ω.
b. Sebaran energi osilator pada harga energi yang diperbolehkan mengikuti
distribusi Boltzmann
f (ε n ) = e −ε n / koT (2.24)
Sebuah osilator dengan satu derajat kebebasan mempunyai energi rata-
rata



∞

∑ε n f (ε n )
ε = n=0
∞

∑ f (ε
n=0
n )

Substitusi (2.23) dan (2.24) ke persamaan di atas menghasilkan
ω
ε = ω / k oT
(2.25)
e −1
Gambar 2.4 berikut menyajikan perbandingan energi kuantum rata-rata osilator
dan energi klasik kristal untuk satu derajat kebebasan.

ε

klasik

kuantum

O T

Gambar 2.4 Energi kuantum rata-rata dan energi klasik rata-rata kristal

Tampak bahwa pada suhu tinggi, sehingga koT>>ћω, osilator berada dalam
keadaan kuantum tereksitasi tinggi. Pada keadaan demikian sifat kuantum
spektrum dapat diabaikan, sehingga dihasilkan energi klasik rata-rata ε = k oT .

Pada suhu rendah, koT<<ћω, dan energi koT tidak cukup untuk mengeksitasikan
osilator ke tingkat eksitasi pertama. Dalam hal ini energi osilator jauh lebih kecil
daripada koT. Oleh karena itu, pada suhu rendah ini, sifat kuantum gerakan lebih
dominan.
Bila zat padat sebanyak 1 kmol dan setiap atom mempunyai 3 derajat
kebebasan, maka energi totalnya
ωE
E = 3N Aε = 3N A ω E / k oT
(2.26)
e −1
dimana ωE adalah frekuensi Einstein (frekuensi bersama osilator). Kapasitas
panas pada volume konstan
2
⎛ ∂E ⎞ ⎛θ ⎞ eθ E / T
CV = ⎜ ⎟ = 3 R⎜ E ⎟ θ / T (2.27)
⎝ ∂T ⎠V ⎝ T ⎠ e E −1
2
( )


dimana θE=(ћωE/ko) adalah suhu karakteristik Einstein. Secara grafik CV di atas
ditunjukkan dalam Gambar 2.5 berikut.

Gambar 2.5 Kapasitas panas tembaga.
Titik-titik merupakan hasil eksperimen.
Kurva mengungkapkan teori Einstein untuk suhu θE=240 K
Secara teori dapat dibuat kurva CV terhadap T/θE yang bentuknya sama untuk
berbagai macam kristal. Data eksperimen (CV,T) suatu kristal tertentu, dapat
dicari kesesuaiannya yang terbaik, sehingga θE dapat ditentukan. Selanjutnya,
frekuensi Einstein ωE pun dapat diperoleh. Untuk θE= 240 K didapatkan ωE =
2,5.1013/s dalam daerah inframerah.
Ungkapan CV di atas menunjukkan hal-hal sebagai berikut.
a. Pada suhu yang sangat tinggi, dimana T>>θE, bentuk eθ E / T dapat diekspansikan
dalam deret pangkat θE/T, sehingga menghasilkan
CV ≅ 3 R
seperti hasil teori klasik.
b. Pada suhu yang sangat rendah, dimana T<<θE, bentuk eθ E / T jauh lebih besar
daripada satu, sehingga
2
⎛θ ⎞
CV ≅ 3R⎜ E ⎟ e −θ E / T ≅ B(T ) e −θ E / T (2.28)
⎝T ⎠
dimana B(T) adalah fungsi yang relatif tidak peka terhadap suhu. Karena
bentuk eksponensial eθ E / T , maka kapasitas panas ini terus berkurang sehingga
mendekati nol dengan cepat sekali. Jadi CV →0 saat T→0. Hal ini sesuai
dengan eksperimen.



Saat mendekati nol mutlak, penurunan CV model Einstein yang secara
eksponensial di atas, ternyata, jauh lebih cepat daripada yang terjadi secara
eksperimen, yakni
CV ∼ T3
Hal ini merupakan kelemahan yang mendasar bagi model Einstein.
Kesimpulan yang dapat ditarik dari model Einstein adalah sebagai berikut.
a. Pada suhu tinggi, osilator tereksitasi sempurna, yang memerlukan energi rata-
rata sebesar koT, sehingga CV ≅ 3 R.
b. Pada suhu rendah, osilator membeku (tidak berosilasi) dalam tingkat energi
dasar sehingga CV=0.

2.1.2.2 Model Debye tentang CV Zat Padat
Untuk menerangkan kebergantungan CV terhadap T, Debye memodelkan
getaran kisi dengan mengambil anggapan sebagai berikut.
a. Atom kristal merupakan osilator yang berkait erat satu sama lain, dengan
daerah frekuensi ω=0 sampai suatu frekuensi maksimum ωD yang ditentukan
oleh jumlah moda getar yang diperkenankan. Dengan demikian pada kristal
terjadi gerakan kisi secara keseluruhan sehingga terdapat moda kisi bersama.
Kristal merupakan medium elastik kontinu.
b. Gelombang suara dalam padatan merupakan contoh moda bersama. Oleh
karena itu moda kisi mempunyai hubungan dispersi linier kontinu (2.5) dan
rapat keadaan (2.18) yang sama dengan bahasan gelombang elastik yang lalu.
Setiap modus getaran merupakan osilator harmonik tunggal ekivalen yang
mempunyai energi rata-rata (2.25) seperti osilator model Einstein. Oleh karena itu
energi total getaran seluruh kisi
3V ω
E = ∫ ε (ω ) g (ω ) dω = 2 3 ∫
ω2 ω / k 0T
dω (2.29)
2π v s e −1
dimana integrasi dilakukan terhadap semua frekuensi yang diperkenankan.
Frekuensi batas bawah, tentunya, adalah ω=0. Sedangkan frekuensi batas
atas ditetapkan oleh debye dengan batasan bahwa jumlah moda yang dicakup



dalam rentang frekuensi tersebut haruslah sama dengan jumlah derajat kebebasan
untuk keseluruhan padatan. Jadi
ωD

∫ g (ω ) dω = 3N
0
A (2.30)

dimana frekuensi atas ωD disebut frekuensi Debye. Hasil integrasi di atas, setelah
mensubstitusikan (2.18) memberikan nilai
ωD = vs (6π2n)1/3 (2.31)
dimana n=NA/V adalah konsentrasi atom dalam padatan.
Energi total (2.29) dapat ditulis kembali
ωD
3V ω3
E=
2π 2 v s3 ∫e ω
0
/ k 0T
−1
dω (2.32)

dan kapasitas panas pada volume konstan
ωD ω / k oT
⎛ ∂E ⎞ 3V 2
ω 4e
CV = ⎜ ⎟ =
⎝ ∂T ⎠V 2π v s k o T
2 3 2 ∫ (e ω
0
/ k oT
−1 )
2
dω (2.33)

Apabila x=(ћω/koT) dan suhu Debye didefinisikan sebagai θD=(ћω/ko), maka
persamaan (2.33) dapat ditulis dalam bentuk
3θ /T
⎛T ⎞ D
x 4e x
CV = 9 R⎜
⎜
⎝θ D
⎟
⎟
⎠
∫ (e
0
x
−1 )2
dx (2.34)

Suhu Debye θD dapat diperoleh dengan mencocokkan kurva eksperimen dari data
(CV,T) suatu kristal dengan kurva universal teoritis CV terhadap T/θD. Untuk suatu
zat tertentu, sudu Debye θD adalah suhu yang dipilih sedemikian rupa sehingga
kurva eksperimen akan berimpit dengan kurva universal teoritis. Bahan berikut ini
Li, Na, K, Cu, Ag, Au, Al, Ga, Pb, Ge, Si, C, NaCl, KCl, CaF2, LiF dan SiO22
pada suhu kamar 300 K, masing-masing memiliki suhu Debye 335; 156; 91,1;
343; 226; 162; 428; 325; 102; 378; 647; 1860; 280; 230; 470; 680; dan 255 K.
Ungkapan CV di atas menunjukkan hal-hal sebagai berikut.
a. Pada suhu tinggi, T>>θD, didapatkan
CV ≅ 3 R



yang sesuai dengan hukum Dulong-Petit. Dalam keadaan demikian, setiap
moda getar tereksitasi penuh, dan memiliki energi klasik rata-rata ε = k oT .
Jika kita substitusikan energi klasik rata-rata tersebut ke dalam (2.29) akan
didapatkan E = 3RT dan CV=3R.
b. Pada suhu rendah, T<<θD, dengan menggunakan hubungan analitik
∞
x 4e x 4 2
∫ (e
0
x
− 1)
2
dx =
15
π

didapatkan
3
12π 4 ⎛ T ⎞
CV = R⎜ ⎟
⎜θ ⎟ (2.35)
5 ⎝ D⎠
Kebergantungan CV terhadap T3 ini sesuai dengan hasil pengamatan. Dalam
keadaan demikian, hanya sedikit moda tereksitasi, yakni moda yang memiliki
energi kuantum ћω, yang lebih kecil daripada kT.

2.2 GETARAN DALAM KISI KRISTAL

Telah dibahas rambatan gelombang dalam padatan sebagai medium
kontinu, yaitu kediskritan kisi dapat diabaikan. Saat panjang gelombang jauh lebih
besar daripada jarak antar atom, yaitu k→0, maka dihasilkan relasi linier ω=vsk.
Tetapi, saat panjang gelombang menurun dan k membesar, maka kediskritan kisi
menjadi berperan karena atom-atom mulai menghamburkan gelombang.
Akibatnya kecepatan menurun, dan dalam hal ini menyebabkan kurva relasi
dispersi tidak lagi linier melainkan mengalami penurunan kemiringan.

2.2.1 Getaran dalam Kisi Linier
2.2.1.1 Kisi Monoatomik Satu Dimensi
Perhatikanlah kisi monoatomik satu dimensi dengan konstanta kisi a
dalam Gambar 2.6 berikut.



ψ -2 ψ -1 ψ ψ +1

a

x -2=( -2)a x -1=( -1)a x= a x +1=( +1)a
Gambar 2.6 Kisi monoatomik satu dimensi

Posisi setimbang atom dinyatakan pada koordinat kisi …, x -1, x , x +1, …

Sedangkan simpangan dari titik setimbang, masing-masing dinyatakan dengan
…, ψ -1, ψ , ψ +1, … Getaran kisi adalah longitudinal.

Andaikan interaksi atom hanya terjadi antartetangga terdekat, gaya yang
bekerja mengikuti hukum Hooke (pendekatan harmonik) dengan konstanta gaya α,
dan massa setiap atom m, maka, sesuai dengan hukum Newton, persamaan gerak
atom ke- adalah

∂2
m ψ l = −α (ψ l − ψ l +1 ) − α (ψ l − ψ l −1 ) = −α (2ψ l − ψ l +1 − ψ l −1 ) (2.36)
∂t 2
Kisi di atas mempunyai simetri translasi, yakni massa atom sama dengan interval
tertentu. Oleh sebab itu diambil bentuk solusi gelombang berjalan
ψ l = Ao e i (kla −ωt ) (2.37)

Solusi (2.37) menunjukkan bahwa semua atom bergetar dengan frekuensi dan
amplitudo sama. Getaran yang demikian disebut getaran modus normal.
Substitusi (2.37) ke dalam (2.36) dan penghilangan besaran-besaran yang sama,
yaitu A, e iω t dan e ikla , serta pemakaian rumus Euler eiy+e-iy=2 cos y
menghasilkan bentuk
ka
ω = ω o sin (2.38)
2
dimana ωo=(4α/m)1/2 dan hanya diambil harga ω positip (yang memiliki arti fisis).
Ungkapan ini tidak lain adalah hubungan dispersi ω(k), yang berbentuk sinusoida



dengan perioda 2π/a dan frekuensi maksimum ωo dalam ruang k, seperti disajikan

ω(k)
kontinu
ωo

-π/a
-2π/a 0 π/a 2π/a

Gambar 2.7 Kurva dispersi ω(k) kisi satu dimensi dengan interaksi tetangga terdekat

Interpretasi fisis yang dapat dikemukakan dari model ini adalah sebagai berikut.
a. Nilai k kecil menyebabkan (2.38) menjadi hubungan dispersi linier, yaitu
⎛ ωoa ⎞
ω ≅⎜ ⎟k (2.39)
⎝ 2 ⎠
Dalam batas ini, kisi berkelakuan sebagai medium kontinu elastik (pegas
kontinu). Harga k kecil, berarti k<<(π/a) atau λ>>2a. Dengan kata lain,
panjang gelombang jauh lebih besar daripada jarak antaratom (sistem makro).
Atom bergerak dalam fasa yang sama satu sama lain. Hal ini menyebabkan
gaya pulih setiap atom menjadi kecil, sehingga ω kecil juga. Kecepatan fasa
vϕ=ω/k sama dengan kecepatan kelompok vg=∂ω/∂k, yaitu sebesar

αa
vϕ= vg=(ωoa)/2= (2.40)
m
Kecepatan fasa vϕ adalah kecepatan perambatan gelombang yang berfrekuensi
ω dan angka gelombang k. Sedangkan kecepatan kelompok vg adalah
kecepatan pulsa gelombang yang berfrekuensi dan angka gelombang rata-rata
ω dan k. Seringkali vg lebih berperan karena yang ditransmisikan gelombang
adalah energi dan momentum.
Kecepatan fasa vϕ tidak lain adalah kecepatan suara (2.6) dalam bahasan
gelombang elastik dahulu. Karena m/a adalah kerapatan massa satu dimensi



dan αa dapat diinterpretasikan sebagai tegangan dalam rantai kisi, maka hal ini
sama dengan bahasan kecepatan rambat gelombang transversal dalam kawat
Melde. Dari (2.40) dan (2.6) dapat dicari hubungan tetapan gaya α dan
modulus Young Y, yaitu
α=aY (2.41)
yang dapat digunakan untuk memprediksi harga α. Untuk nilai a= 5.10-8cm dan
Y= 1011 gr/cm s2 didapatkan nilai α= 5.103 dyne/cm. Kasus dengan k<<π/a,
atau λ>>a dinamakan batas gelombang panjang.
b. Saat k membesar terjadi deviasi secara signifikan terhadap bentuk linier. Pada
k=±π/a terdapat nilai frekuensi maksimum. Nilai k=±π/a, berarti λ=2a,
menyebabkan atom yang bertetangga bergetar dengan fasa berlawanan,
sehingga gaya pulih dan frekuensi menjadi maksimum. Karena adanya fasa
berlawanan pada dua atom berdekatan, maka terjadi gelombang pantulan.
Akibatnya terjadi superposisi antara gelombang datang dan pantul oleh semua
atom dalam kristal, dan menghasilkan gelombang berdiri. Dalam kasus ini
kecepatan kelompok vg=0. Kasus dengan k=±π/a dinamakan kondisi refleksi
Bragg.
Frekuensi maksimum ωo=(4α/m)1/2 yang bergantung pada konstanta pegas dan
massa atom adalah memang sifat untuk osilator harmonik. Dengan
mensubstitusikan nilai α= 5.103 dyne/cm dan m= 22.10-24 gr (untuk hidrogen)
didapatkan nilai ωo= 2.1013/s dalam daerah inframerah.
c. Nilai k=0, berarti λ=∞, menyebabkan keseluruhan bagian kristal bertranslasi,
sehingga gaya pulih menjadi nol. Hal ini berarti ω=0 untuk k=0.

Lihat kembali kurva dispersi (Gambar 2.7) di atas. Tampak bahwa kurva
tersebut periodik dalam ruang k, dan simetri terhadap pencerminan di sekitar titik
asal k=0. Oleh karena itu daerah yang penting adalah 0<k<π/a. Hanya frekuensi
dalam rentang 0<ω<ωo yang ditransmisikan dalam kisi. Frekuensi di atas ωo
mengalami atenuasi tajam. Dalam hal ini, kisi berperan sebagai filter mekanik
lolos rendah.
Periodisitas ω(k) dalam ruang k mempunyai perioda 2π/a. Oleh karena itu



ω(k + 2π/a) = ω(k) (2.42)
Perhatikanlah contoh sederhana dalam Gambar 2.8 berikut.

Gambar 2.8 Gelombang transversal dengan λ=4a dan λ=(4/5)a

Angka gelombang keduanya, masing-masing k=π/2a dan k’=(k+2π/a). Terlihat
bahwa keduanya merepresentasikan gerakan fisis yang sama. Oleh karena itu dua
moda tersebut haruslah mempunyai frekuensi yang sama. Secara umum, hal ini
berlaku untuk dua titik sebarang k dan k’, dimana k’=(k + n 2π/a) untuk n
bilangan bulat. Hal inilah yang menyebabkan frekuensi ω merupakan fungsi
periodik dari k dengan perioda 2π/a.
Dalam kisi diskrit, panjang gelombang suatu gelombang bukanlah besaran
unik. Begitu juga nilai k, masing-masing nilai k yang ekivalen ditranslasikan
sejauh n(2π/a) satu terhadap yang lain dalam ruang k. Pilihan interval tertentu
dalam ruang k, yakni sama dengan periodanya sebesar 2π/a, diperlukan untuk
membuat representasi k maupun λ menjadi unik.
Panjang gelombang terpendek dari gelombang dalam kristal linier yang
masih memiliki makna fisis adalah
λ=2a
yang bersesuaian dengan k=π/a. Oleh karena itu semua getaran, λ=0 sampai λ=∞,
yang memiliki makna fisis berada dalam interval
0 < |k| < π/a
Daerah antara (-π/a < k < π/a) dinamakan Zona Brillouin Pertama, yang
merepresentasikan semua gelombang yang masih memiliki makna fisis dalam
kristal. Jumlah moda getar dalam zona ini sama dengan jumlah total atom dalam
kisi.



Simetri refleksi terhadap titik nol dalam ruang k, berarti
ω(-k) = ω(k) (2.43)
Moda k merepresentasikan gelombang yang merambat ke arah kanan dan –k ke
arah kiri dalam kisi. Karena kisi ekivalen dalam kedua arah tersebut, maka
frekuensinyapun harus sama seperti di atas.

2.2.1.2 Kisi Diatomik Satu Dimensi
Model ini terdiri dari dua jenis atom, masing-masing bermassa M1 pada
koordinat ganjil, dan M2 pada koordinat genap. Jarak setimbang atom bertetangga
sebesar a.

a M2
M1

x2 -3 x2 -2 x2 -1 x2

Gambar 2.9 Kisi diatomik satu dimensi
Asumsi yang digunakan sama dengan bahasan kisi monoatomik. Persamaan gerak
untuk masing-masing massa
∂2
M1 ψ 2l +1 = −α (2ψ 2l +1 − ψ 2l − ψ 2l + 2 )
∂t 2
(2.44)
∂2
M 2 2 ψ 2l + 2 = −α (2ψ 2l + 2 − ψ 2l +1 − ψ 2l +3 )
∂t
Diambil solusi berbentuk
ψ 2l +1 = A1e i [ka (2l +1)−ωt ]
(2.45)
ψ 2l + 2 = A2 e i [ka (2l + 2 )−ωt ]
Substitusi bentuk solusi (2.45) ke dalam persamaan (2.44) menghasilkan dua
persamaan yang ekivalen persamaan matrik
⎛ 2α − M 1ω 2 − 2α cos(ka )⎞⎛ A1 ⎞
⎜ ⎟⎜ ⎟
⎜ − 2α cos(ka ) 2α − M ω 2 ⎟⎜ A ⎟ = 0 (2.46)
⎝ 2 ⎠⎝ 2 ⎠
Solusi nontrivial persamaan homogen (2.46) ada hanya jika harga determinan
matrik sama dengan nol. Oleh karena itu persamaan sekularnya
2α − M 1ω 2 − 2α cos(ka )
=0 (2.47)
− 2α cos(ka ) 2α − M 2ω 2



yang merupakan persamaan kuadrat dalam ω2, dan memberikan solusi untuk ω2,
yakni
1/ 2
⎛ 1 1 ⎞ ⎧⎛ 1
⎪ 1 ⎞
2
4 sin 2 (ka ) ⎫
⎪
ω 2
1, 2 = α⎜
⎜ + ⎟ ± α ⎨⎜
⎟ ⎜M + M ⎟ −
⎟ ⎬ (2.48)
⎝ M1 M 2 ⎠ ⎪⎝ 1
⎩ 2 ⎠ M 1M 2 ⎪
⎭
Tanda ± menyebabkan terdapat dua hubungan dispersi, yang masing-masing
kurvanya, dengan asumsi M1< M2, disajikan dalam Gambar 2.10 berikut.

Gambar 2.10 Dua cabang dispersi kisi diatomik M1< M2
Kurva bawah, bersesuaian dengan tanda minus, dinamakan cabang akustik. Kurva
ini memiliki ciri sama dengan kisi monoatomik. Sedangkan kurva atas dinamakan
cabang optik karena dihasilkan frekuensi optik dalam spektrum elektromagnet.
Variasi cabang ini tidak begitu besar, sehingga sering dianggap tetap.

Pada gambar di atas terdapat daerah tanpa getaran, yaitu daerah frekuensi
antara (2α/M2)1/2 sampai (2α/M1)1/2. Untuk harga α= 5.103dyne/cm dan M=10-23
gr didapatkan frekuensi ω=(2α/M)1/2= 3.1013/s dalam daerah inframerah. Daerah
terlarang ini, dimana kisi tidak dapat mentransmisikan gelombang, disebut celah
frekuensi. Oleh karena itu, kisi diatomik berperan sebagai filter mekanik lolos
pita.

Perbedaan dinamika getaran antara kedua cabang di atas dapat dipelajari
dari perbandingan amplitudo A1/ A2 pada nilai k=0 (atau λ=∞).



Cabang akustik. Substitusi ω1=0 ke dalam persamaan matrik (2.46) menghasilkan
ungkapan
A1 = A 2 (2.49)
Hal ini berarti dua atom dalam sel, atau molekul, mempunyai amplitudo dan fasa
yang sama. Keseluruhan kisi bergetar seperti benda tegar, dengan pusat massa
bergerak bolak-balik, seperti Gambar 2.11 berikut.

Gambar 2.11 Getaran cabang akustik pada k=0
1/ 2
⎧ ⎛ 1 1 ⎞⎫
Cabang optik. Substitusi ω 2 = ⎨2α ⎜
⎜ M + M ⎟⎬⎟ ke dalam persamaan matrik
⎩ ⎝ 1 2 ⎠⎭

(2.46) di atas menghasilkan ungkapan
M1 A1 + M2 A2 = 0 (2.50)
Hal ini berarti cabang optik berosilasi dengan pusat massa atom tidak berubah.
Dua atom dalam sel bergetar dalam fasa berlawanan, seperti pada Gambar 2.12
berikut.

Gambar 2.12 Getaran cabang optik pada k=0
Lihat kembali kurva dispersi kisi diatomik (Gambar 2.10) di atas. Tampak
bahwa kurva tersebut periodik dalam ruang k dengan perioda π/a dan mempunyai
simetri refleksi di sekitar titik k=0. Zona Brillouin Pertama terletak pada daerah
(π/2a<k<π/2a). Hal ini berkaitan dengan perioda kisi riilnya sebesar 2a. Dalam



zona ini, jumlah nilai k yang diperkenankan sebanyak jumlah atom total N.
Karena terdapat dua cabang, maka jumlah moda getar totalnya adalah 2N.

2.2.1.3 Kisi Tiga Dimensi
Misalnya, terdapat kisi Bravais tiga dimensi dengan satu atom persel
satuan. Diandaikan bentuk solusi gelombang yang merambat dalam kristal

ψ n = Ae i (k •r −ωt ) (2.51)

Vektor amplitudo A menunjukkan arah getaran atom yang sesuai dengan
polarisasi gelombang (longitudinal [ A paralel k ], transversal [ A tegak lurus k ]
atau keduanya).
Substitusi solusi (2.51) ke dalam persamaan gerak, menghasilkan
perangkat tiga persamaan yang melibatkan Ax, Ay dan Az, sehingga diperoleh
persamaan sekular dengan determinan matrik 3x3. Akhirnya diperoleh
3 buah harga ω2
yang semuanya melalui titik asal k=0 (cabang akustik). Fungsi dispersi termaksud
tidak perlu isotropik dalam ruang k untuk arah yang berbeda dalam kristal.
Kisi non-Bravais tiga dimensi, dalam tiap sel satuannnya mengandung dua
atau lebih atom. Misalnya, terdapat r atom persel, maka akan terdapat 3r kurva
dispersi, yang terdiri dari 3 cabang akustik, dan (3-r) cabang optik.

RINGKASAN
01. Padatan terdiri dari atom diskrit yang berosilasi di sekitar titik setimbangnya
sebagai akibat adanya energi termal. Jika gelombang yang merambat
mempunyai panjang gelombang yang jauh lebih besar daripada jarak
antaratom, maka sifat atomik dapat diabaikan dan padatan dapat dianggap
sebagai medium kontinu (lingkup makro). Gelombang yang demikian disebut
gelombang elastik. Bahasan ini menghasilkan hubungan dispersi linier ω = vs



k, dimana vs = (Y/ρ)1/2 adalah kecepatan fasa gelombang. Bila dikenai syarat
3V ω 2
batas periodik, maka diperoleh rapat keadaan g (ω ) =
2π 2 v s3
02. Menurut teori klasik setiap atom dalam kristal, disamping memiliki 3 derajat
kebebasan untuk geraknya di sekitar kedudukan setimbangnya (energi kinetik),
juga memiliki energi potensial atom dalam gerak harmoniknya; sehingga
energi total sistem atom dalam kristal menurut hukum ekipartisi U = 3RT .
Dengan demikian kapasitas panas kristal pada volume konstan adalah CV=3R,
yang sesuai dengan penemuan empirik Dulong-Petit (1819), yang berlaku
untuk hampir semua zat padat pada suhu ruang atau yang lebih tinggi. Tetapi,
hal ini tidak sesuai dengan hasil eksperimen.
02. Hasil eksperimen menunjukkan bahwa nilai CV berharga 3R pada suhu tinggi,
menurun apabila T menurun, dan mendekati nol apabila T menuju 0 K.
Disamping itu, terdapat indikasi yang sangat kuat bahwa pada suhu yang
sangat rendah mendekati nol mutlak CV ∼ T3.
03. Model Einstein tentang CV zat padat mengandaikan bahwa atom kristal
merupakan osilator independen, yang masing-masing memiliki frekuensi sama
dan energi diskrit εn=n ћ ω , n = 0, 1, 2, …, dan sebaran energi osilator pada
harga energi yang diperbolehkan mengikuti distribusi Boltzmann
f (ε n ) = e −ε n / koT . Berdasarkan andaian ini diperoleh kapasitas panas
2
⎛θ ⎞ eθ E / T
CV = 3R⎜ E ⎟ , yang hanya cocok untuk suhu tinggi dan
⎝ T ⎠ eθ E / T − 1(2
)
mendekati 0 K
04. Model Debye tentang CV zat padat mengandaikan bahwa atom kristal
merupakan osilator yang berkait erat satu sama lain, dengan daerah frekuensi
ω=0 sampai suatu frekuensi maksimum ωD yang ditentukan oleh jumlah moda
getar yang diperkenankan. Dari andaian ini diperoleh kapasitas panas
3θ /T
⎛T ⎞ D
x 4e x
CV = 9 R⎜
⎜θ
⎝ D
⎟
⎟
⎠
∫ (e
0
x
−1 )
2
dx , yang sesuai dengan hasil eksperimen.



05. Getaran kisi monoatomik satu dimensi menghasilkan hubungan dispersi
ka
ω = ω o sin . Kisi hanya bisa merambatkan frekuensi di bawah ωo. Oleh
2
karena itu kisi ini dapat berperan sebagai filter mekanik lolos rendah. Pada
nilai k kecil terjadi hubungan dispersi linier, yang mengakibatkan panjang
gelombang jauh lebih besar daripada jarak antaratom (sistem makro) atau atom
bergerak dalam fasa yang sama satu sama lain. Pada nilai k=±π/a, berarti λ=2a,
menyebabkan atom yang bertetangga bergetar dengan fasa berlawanan (terjadi
gelombang berdiri), sehingga gaya pulih dan frekuensi menjadi maksimum.
Sedangkan pada nilai k=0, berarti λ=∞, menyebabkan keseluruhan bagian
kristal bertranslasi, sehingga gaya pulih menjadi nol. Hal ini berarti ω=0 untuk
k=0.
06. Getaran kisi diatomik satu dimensi menghasilkan dua hubungan dispersi,
yakni cabang optik dan akustik
1/ 2
⎛ 1 1 ⎞ ⎧⎛ 1
⎪ 1 ⎞
2
4 sin 2 (ka ) ⎫
⎪
ω 2
1, 2 = α⎜
⎜M + M ⎟ ± α ⎨⎜
⎟ ⎜M + M ⎟ −
⎟ ⎬ . Pada getaran ini
⎝ 1 2 ⎠ ⎪⎝ 1
⎩ 2 ⎠ M 1M 2 ⎪
⎭
terdapat daerah tanpa getaran, yang disebut celah frekuensi. Oleh karena itu,
kisi diatomik berperan sebagai filter mekanik lolos pita. Pada nilai k=0, untuk
cabang akustik didapatkan bahwa A1=A2, yang artinya dua atom dalam sel,
atau molekul, mempunyai amplitudo dan fasa yang sama. Keseluruhan kisi
bergetar seperti benda tegar, dengan pusat massa bergerak bolak-balik.
Sedangkan untuk cabang optik menghasilkan M1 A1 + M2 A2 = 0, yang artinya
bahwa cabang optik berosilasi dengan pusat massa atom tidak berubah. Dua
atom dalam sel bergetar dalam fasa berlawanan.

LATIHAN SOAL BAB II
01. Hasil pengukuran dalam suatu jenis padatan menunjukkan bahwa kecepatan
gelombang vs=5.105 cm/s dan rapat massa ρ=5 gr/cm3. Berapakah modulus
Young padatan tersebut?



02. Dengan menggunakan distribusi Maxwell-Boltzmann dan hukum ekipartisi
energi, tunjukkan bahwa osilator harmonis satu dimensi pada kesetimbangan
termal mempunyai energi rata-rata ε = k o T !

03. Jika harga konstanta gas umum R≅2 kal/mol K, maka hitunglah kapasitas
panas pada volume tetap padatan pada suhu tinggi!
04. Tunjukkan penurunan persamaan (2.25)!
05. Tembaga mempunyai suhu Einstein θE=240 K. Berapa dan terletak di daerah
optik mana frekuensi Einstein tersebut?
06. Jika diketahui bahwa suatu padatan mempunyai konsentrasi atom n=1022
atom/cm3 dan kecepatan gelombang vs=5.105 cm/s, maka hitunglah frekuensi
Debye ωD!
07. Kemukakan sampai sejauh mana kesesuaian (terhadap rentang suhu) kapasitas
panas padatan ramalan (a) Dulong-Petit, (b) Einstein, dan (c) Debye dengan
hasil pengamatan!
08. Tunjukkan penurunan persamaan (2.41)!
09.a. Jika konstanta kisi a=5 Å dan modulus Young Y=1011 gr/cm s2, maka
tentukan konstanta gaya α!
b. Dengan menggunakan harga α dari soal a), dan massa m=2.10-24 gr (untuk
hidrogen), maka tentukan frekuensi maksimum ωo!
10. Anggaplah bahwa kisi kristal satu dimensi merupakan medium kontinu dan
mempunyai syarat batas periodik. Buktikan bahwa jumlah moda getar dalam
Zona Brillouin Pertama (ZBP) adalah sama dengan jumlah total atom, atau
jumlah sel satuan dalam kisi!
11. Semua getaran yang memiliki makna fisis berada dalam interval ZBP
⎛ π⎞ ⎛ π⎞
⎜ − ⎟ ≤ k < ⎜ + ⎟ . Sesuai dengan soal nomor (10), maka jika terdapat N
⎝ a⎠ ⎝ a⎠
atom, maka nilai k yang diperbolehkan akan sebanyak N pula, yang terentang
2π 1 2π 1
dari − 2 N hingga + N . Misalnya terdapat vibrasi gelombang yang
Na Na 2
merambat dalam kristal monoatomik satu dimensi dengan jarak setimbang



antaratom a=5 Å. Jika kristal mengandung 6,00.108 atom, maka tentukan
rentang angka gelombang k yang diperbolehkan!
12. Tunjukkan bahwa untuk harga ka kecil, maka dari persamaan (2.48) dapat
diperoleh
⎛ 1 1 ⎞ 2α
a. dua harga frekuensi ω 2 = 2α ⎜
⎜M + M ⎟ dan ω 2 =
⎟ (ka) 2
⎝ 1 2 ⎠ M1 + M 2

2α a 2
b. kecepatan fasa bunyi v = (Tampak bahwa dengan (M1+M2)/a
M1 + M 2

adalah kerapatan massa satu dimensi, maka hal ini sama dengan bahan
pegas/kawat kontinu dengan tegangan 2αa)
13. Tunjukkan bahwa untuk harga k=π/2a, maka dari persamaan (2.48) diperoleh
dua harga frekuensi ω 2 = 2α / M 1 dan ω 2 = 2α / M 2
14. Kemukakan yang terjadi pada Gambar 2.10, jika diasumsikan bahwa M1>M2!
15. Tunjukkan bahwa celah frekuensi dalam vibrasi kisi diatomik satu dimensi
a. semakin tajam bila kedua massa semakin tidak sama!
b. lenyap bila kedua massa sama besar!
16. Buktikan bahwa pada k=π/2a dalam kisi diatomik satu dimensi
a. cabang akustik menunjukkan bahwa hanya atom berat yang bervibrasi!
b. cabang optik menunjukkan bahwa hanya atom ringan yang bervibrasi!
17. Sama dengan soal (10), tetapi untuk kisi kristal diatomik satu dimensi.
Buktikan bahwa jumlah moda getarnya dua kali lebih besar karena masing-
masing angka gelombang k bersesuaian dengan dua moda, yaitu moda akustik
dan optik!
18. Harga kecepatan fasa bunyi dalam padatan berorde 3.103 m/s daan jarak
antaratomnya berorde 3 Å. Jika padatan diasumsikan sebagai sebuah kisi linier,
maka berapakah harga frekuensi maksimumnya?
19. Kecepatan kelompok bunyi suatu rantai linier monoatomik adalah 1,08.104
m/s. Jika massa tiap atom 6,81.10-26 kg dan jarak setimbang antaratom 4,85 Å,
maka
a. berapakah konstanta gaya?



b. berapakah frekuensi angular maksimum?
20. Tunjukkan penurunan persamaan (2.49) dan (2.50)!
21. Tunjukkan bahwa untuk panjang gelombang yang jauh lebih besar daripada
jarak antaratom, maka persamaan gerak (2.36) dapat direduksi menjadi
∂2 ∂2
persamaan gelombang elastik kontinum ψ l = v 2 2 ψ l , dengan v adalah
∂t 2 ∂x
kecepatan fasa bunyi!
22. Getaran kisi bujursangkar
Diasumsikan terdapat getaran transversal pada kisi bidang bujursangkar
monoatomik. Ambillah u ,m pergeseran yang normal terhadap bidang kisi dari

atom dalam kolom ke- dan baris ke-m. Setiap atom bermassa m dan konstanta

gaya α untuk interaksi tetangga terdekat.
a. Buktikan bahwa persamaan geraknya adalah
m (d2 u ,m/dt2) = α [(u +1,m + u -1,m - 2 u ,m) + (u ,m+1 + u ,m-1 - 2 u ,m) !

b. Ambillah solusi berbentuk u ,m = u(0) exp[I( kxa + mkya - ωt)], dimana a

adalah jarak antara tetangga terdekat atom. Buktikan bahwa relasi dispersi
yang sesuai adalah ω2 m = 2 α (2 - cos kxa - cos kya) !
c. Buktikan untuk ka << 1 dipenuhi ω=(αa2/m)1/2 (kx2+ ky2)1/2= (αa2/m)1/2 k,
sehingga memiliki kecepatan yang konstan!


B A B III
ELEKTRON DALAM LOGAM I
(MODEL ELEKTRON BEBAS)
Logam memegang peranan penting dalam kehidupan manusia, misalnya besi
dalam produksi otomobil, tembaga untuk penghantar listrik dan lain-lain. Umumnya,
logam memiliki sifat kekuatan fisik tinggi, kerapatan tinggi, konduktivitas listrik dan
termal baik, dan daya refleksi tinggi. Sifat ini berkaitan dengan struktur mikroskopis
bahan, yang dapat diasumsikan bahwa suatu logam mengandung elektron bebas,
dengan konsentrasi besar, yang dapat bergerak dalam keseluruhan volume kristal.
Saat atom bebas membentuk logam, semua elektron valensi menjadi elektron
konduksi dalam logam. Elektron konduksi bergerak bebas di antara ion, sehingga
keadaannnya berubah tajam. Berbeda dengan elektron “cores” yang tetap terlokalisasi
sehingga karakternya relatif tidak berubah. Dengan demikian, gambaran sederhana
tentang kristal logam adalah suatu kisi ion teratur dalam ruang, dan elektron bebas
bergerak di antara ion tersebut. Gambaran lebih lengkapnya, bahwa ion bergetar
secara termal di sekitar titik setimbang, dan demikian pula elektron bebas bergerak
termal di antara ion kristal dan merubah arah geraknya setiap kali menumbuk ion
(kemungkinan besar) atau elektron lain (kemungkinan kecil).
Dalam logam Na, proporsi volume yang terisi oleh ion “cores” hanya sekitar
15%. Hal ini terjadi karena radius ion Na+ adalah 0,98 Å; sedangkan setengah jarak
antartetangga terdekat atom adalah 1,83 Å. Konsentrasi elektron konduksi dapat
dihitung dari valensi dan kerapatan logam. Jika ρm dan ZV, masing-masing adalah
kerapatan bahan dan valensi atom, maka konsentrasi elektronnya adalah
ρm N A
n = ZV (3.1)
M

3 MODEL ELEKTRON BEBAS 73

dengan NA adalah bilangan Avogadro dan M adalah berat atom. Logam memiliki
konsentrasi elektron yang besar, yakni n = 1029/m3. Misalnya, logam Na, K, Cu, Ag
dan Au adalah monovalen; dan logam Be, Mg, Zn dan Cd adalah divalen.
Bagian awal bab ini membahas perkembangan model elektron bebas. Bahasan
kapasitas panas dan suseptibilitas magnetik dari sumbangan elektron menunjukkan
bahwa yang sesuai dengan eksperimen adalah hanya jika elektron mengikuti prinsip
eksklusi Pauli. Kemudian, dikenalkan konsep tingkatan Fermi dan permukaan Fermi,
yang dapat digunakan untuk memperjelas deskripsi konduktivitas listrik dalam
logam.
Dalam bab ini juga dibahas pengaruh medan magnet terhadap gerakan
elektron bebas, yakni efek Hall dan resonansi siklotron. Bahasan kedua hal ini
menghasilkan informasi yang mendasar tentang logam.
Dalam model elektron bebas ini elektron mengalami tumbukan dengan fonon
dan ketidakmurnian. Hal ini menghasilkan ungkapan hukum Matthiessen. Selain itu,
elektron dapat melepaskan diri dari permukaan logam sehingga terjadi emisi
thermionik. Akhirnya, bab ini ditutup dengan dikemukakannya beberapa kegagalan
model elektron bebas dalam membahas sifat logam.

3.1 MODEL ELEKTRON BEBAS KLASIK
3.1.1 Teori Drude tentang Elektron dalam Logam
Drude (1900) mengandaikan bahwa dalam logam terdapat elektron bebas,
yang membentuk sistem gas elektron klasik, yang bergerak acak dalam kristal dengan
kecepatan random vo karena energi termal dan berubah arah geraknya setelah
bertumbukan dengan ion logam. Karena massanya yang jauh lebih besar, maka ion
logam tidak terpengaruh dalam tumbukan ini.
Kehadiran medan listrik ε dalam logam hanya mempengaruhi gerak
keseluruhan electron karena ion-ion tertata berjajar dan bervibrasi di sekitar titik kisi
sehingga tidak memiliki neto gerak translasi. Misalnya, terdapat medan listrik ε
dalam arah sumbu-X. Percepatan elektron yang timbul



eε
ax = − (3.2)
m*
dengan e dan m*, masing-masing adalah muatan dan massa efektif elektron. Jika
waktu rata-rata antara dua tumbukan elektron dan ion adalah τ, maka kecepatan
hanyut dalam selang waktu tersebut
eε
v hanyut = vo − τ (3.3)
m*
Oleh karena itu rapat arus yang terjadi
⎡ ⎛ eε ⎞⎤
J x = ∑ ⎢− e⎜ vo − τ⎟ (3.4)
⎣ ⎝ m * ⎠⎥⎦
dimana penjumlahan dilakukan terhadap semua elektron bebas setiap satuan volume.
Elektron bergerak secara acak, sehingga ∑vo=0. Oleh sebab itu ungkapan (3.4)
menjadi
e 2 nτ
Jx = ε (3.5)
m*
Karena hubungan Jx=σε, maka menurut (3.5) konduktivitas listrik memiliki ungkapan
e 2 nτ
σ = (3.6)
m*
Pengukuran menunjukkan bahwa nilai rata-rata σ logam sekitar 5.107(Ωm)-1. Dengan
menganggap masa efektif m* sama dengan massa bebas mo=9,1.10-31kg, maka
didapatkan nilai τ berorde 10-14 s.
Contoh analisa lain adalah konduktivitas termal. Misalnya, sepanjang sumbu-
X terdapat gradien suhu ∂T/∂x, maka akan terjadi aliran energi persatuan luas
perdetik (arus kalor) Qe. Berdasarkan eksperimen arus kalor Qe tersebut sebanding
dengan gradien suhu ∂T/∂x
Qe = -K ∂T/∂x (3.7)
dengan K adalah konduktivitas termal. Dalam isolator, panas dialirkan sepenuhnya
oleh fonon. Sedangkan dalam logam dialirkan oleh fonon dan elektron. Tetapi karena
konsentrasi elektron dalam logam sangat besar, maka konduktivitas termal fonon jauh



lebih kecil daripada elektron, yakni Kfonon≅10-2Kelektron, sehingga konduktivitas fonon
diabaikan.
Dari pendekatan teori kinetik gas diperoleh ungkapan konduktivitas termal
K = (1/3) CV v (3.8)

dimana CV, v dan masing-masing adalah kapasitas panas elektron persatuan

volume, kecepatan partikel rata-rata dan lintas bebas rata-rata partikel. Karena
CV=(3/2)nk, (1/2)mv2=(3/2)kT dan =vτ, maka konduktivitas (3.8) menjadi

3 nk 2Tτ
K= (3.9)
2 mo
Perbandingan konduktivitas termal (3.9) dan listrik (3.6) adalah
2
K 3⎛k ⎞
= ⎜ ⎟ T (3.10)
σ 2⎝ e⎠
Hal ini sesuai dengan penemuan empirik oleh Wiedemann-Frans (1853). Kadang-
kadang perbandingan (3.10) di atas dinyatakan sebagai bilangan Lorentz
K
L= (3.11)
σT
Ternyata, hukum Wiedemann-Frans sesuai dengan pengamatan untuk suhu tinggi
(termasuk suhu kamar) dan suhu sangat rendah (beberapa K). Tetapi, untuk suhu
“intermediate”, K/σT bergantung pada suhu.
Dalam teori drude, lintas bebas rata-rata elektron bebas, =τvo, tidak

bergantung suhu. Namun, karena vo∼T1/2, maka keadaan mengharuskan
τ ∼ T-1/2
Hal ini didukung fakta eksperimen bahwa σ∼T-1, sehingga dari ungkapan
konduktivitas listrik didapatkan
n τ ∼ T-1 atau n ∼ T-1/2
Ungkapan terakhir ini menunjukkan bahwa bila T naik, maka n menurun. Hal ini
tidak sesuai dengan fakta, dan menyebabkan teori Drude tidak memadai.



3.1.2 Model Elektron Bebas Klasik
Model elektron bebasa klasik tentang logam mengambil andaian berikut.
a. Kristal digambarkan sebagai superposisi dari jajaran gugus ion positip (yang
membentuk kisi kristal) dan elektron yang bebas bergerak dalam volume kristal.
b. Elektron bebas tersebut diperlakukan sebagai gas, yang masing-masing bergerak
secara acak dengan kecepatan termal (seperti molekul dalam gas ideal – tidak ada
tumbukan, kecuali terhadap permukaan batas)
c. Pengaruh medan potensial ion diabaikan, karena energi kinetik elektron bebas
sangat besar.
d. Elektron hanya bergerak dalam kristal karena adanya penghalang potensial di
permukaan batas.
Misalnya, setiap atom memberikan ZV elektron bebas, maka jumlah total
elektron tersebut perkilomol
n = ZV NA
Bila elektron berperilaku seperti dalam gas ideal, maka energi kinetik totalnya
U = n (3/2) k T = (3/2) ZV R T (3.12)
sehingga kapasitas panas sumbangan elektron bebas
(CV)el = (3/2) ZV R (3.13)
Kapasitas panas total dalam logam, termasuk sumbangan oleh fonon, adalah
CV = (CV)f + (CV)el = [3 + (3/2) ZV) R (3.14)
Jadi, setidaknya kapasitas panas logam harus 50% lebih tinggi daripada isolator.
Tetapi, eksperimen menunjukkan bahwa untuk semua bahan padatan (logam dan
isolator) nilai CV mendekati 3R pada suhu tinggi. Pengukuran yang akurat
menunjukkan bahwa sumbangan elektron bebas terhadap kapasitas panas total adalah
reduksi harga klasik (3/2)R oleh factor 10-2. Oleh karena itu model elektron bebas
klasik tidak memberikan hasil ramalan CV yang memadai.
Suseptibilitas magnetik χ mengkaitkan momen magnetik M dan kuat medan
magnetik H melalui ungkapan



M =χ H (3.15)
Dalam hal ini hanya dibahas untuk bahan isotropik, sehingga χ skalar. Pengaruh

medan magnet luar H terhadap elektron bebas menyebabkan setiap momen dipol μ ,
yang acak arahnya, memperoleh energi magnetik
E = −μ • H (3.16)
Jika distribusi momen dipol elektron bebas memenuhi statistik Maxwell-Boltzmann,
yakni f(E)=e-E/kT, maka momen dipol rata-rata dalam arah medan memenuhi
π

∫ μ cosθ e 2π sin θ dθ
− E / kT

μ= 0
π
(3.17)
∫e 2π sin θ dθ
− E / kT

0

dimana θ adalah sudut antara μ dan H. Hasil dari persamaan (3.17) adalah
μ = μ L(x) (3.18)
dengan L(x)=coth x – (1/x) = fungsi Langevin
x = (μH/kT)
Dengan menggunakan deret
1 x x3 2x5
coth x = + − + + ... , untuk 0< x <π
x 3 45 945
maka untuk medan H tidak kuat, yakni μH<<kT momen dipol rata-rata tersebut
berharga
1μH
μ =μ (3.19)
3 kT
Jika jumlah momen dipol magnet adalah N, maka magnetisasinya
Nμ 2
M = Nμ = H (3.20)
3kT
Dengan membandingkan (3.20) dan (3.15) diperoleh suseptibilitas magnetik
Nμ 2
χ= (3.21)
3kT



Tetapi, eksperimen tidak menunjukkan adanya kebergantungan χ terhadap T. Hal ini
berarti model elektron bebas klasik tidak dapat menerangkan tentang mengapa χ
untuk paramagnet elektron tidak bergantung pada T.

3.2 MODEL ELEKTRON BEBAS TERKUANTISASI
Untuk memperbaiki kegagalan model elektron bebas klasik dalam menelaah
sifat listrik dan magnet bahan, ditawarkan model elektron bebas yang terkuantisasi.
Model ini menggunakan prinsip kuantisasi energi elektron dan prinsip eksklusi Pauli
untuk elektron yang melibatkan distribusi Fermi-Dirac.
Model elektron bebas, dimana pengaruh dari semua elektron bebas yang lain
dan semua ion positip direpresentasikan oleh potensial V sama dengan nol sehingga
gaya yang bekerja pada elektron juga sama dengan nol, secara kuantum mengambil
persamaan Schrodinger
2
− ∇ 2ψ (r ) = Eψ (r ) (3.22)
2mo
dengan solusi fungsi elektron

ψ (r ) = Ao e ik •r (3.23)

dan energi elektron
2
k2
Ek = (3.24)
2mo
Harga k tidak dibatasi sehingga energi elektron tidak terkuantisasi. Tetapi bila
elektron bebas tersebut bergerak dalam suatu kubus dengan rusuk L, maka haruslah
dipenuhi
2
⎛ 2π ⎞ 2
k =k +k +k =⎜
2 2
x
2
y
2
z (
⎟ nx + n y + nz
2 2
) (3.25)
⎝ L ⎠
n x = n y = n z = 0, ± 1, ± 2, ...

Dalam ruang k, setiap keadaan elektron direpresentasikan oleh volume
sebesar (2π/L)3, yaitu masing-masing untuk Δnx=Δny=Δnz=1. Semua keadaan



(k + k y + k z2 ) terletak pada permukaan bola
2
elektron yang berenergi E k = 2
x
2

2mo
berkari-jari k yang memenuhi

(
k 2 = k x2 + k y + k z2 =
2
) 2mo
2
Ek

Sedangkan semua keadaan elektron yang berenergi antara E dan E+dE terletak dalam
kulit bola dengan jari-jari antara k dan k+dk dan volume 4πk2dk. Dengan demikian,
jumlah keadaan elektron
4π k 2 dk L3 k 2
=
(2π L)
dk
3
2π 2

Apabila diperhitungkan dua spin elektron, maka jumlah tersebut menjadi
L3 k 2
dk
π2
Mengingat ungkapan E=ћ2k2/2mo, maka jumlah keadaan elektron persatuan volume
yang berenergi antara E dan E+dE adalah
3/ 2
k2
1 ⎛ 2 mo ⎞
g ( E ) dE = 2 dk = ⎜ ⎟ E 1 / 2 dE (3.26)
π 2π 2 ⎝ 2 ⎠
Prinsip Pauli menyatakan bahwa dalam satu sistem fisis tidak boleh terdapat
dua elektron atau lebih yang mempunyai perangkat bilangan kuantum yang tepat
sama. Prinsip larangan ini dipenuhi oleh elektron yang mengikuti fungsi distribusi
Fermi-Dirac
1
f (E) = ( E − E F ) / kT (3.27)
1+ e
Pada suhu T=0 K, energi Fermi diungkapkan dalam bentuk EF(0); dan fungsi
distribusi Fermi-Dirac
1
untuk E < EF(0) → f ( E ) = =1
1 + e −∞
1
untuk E > EF(0) → f ( E ) = =0
1 + e∞



Dengan kata lain, pada suhu T=0 K semua tingkat energi E<EF(0) terisi penuh
elektron dan E>EF(0) kosong. Sedangkan pada suhu T>0 K berlaku
untuk E < EF → f(E) < 1
untuk E = EF → f(E) = 1/2
untuk E > EF → f(E) > 0
Hal ini berarti pada T>0 K tingkat energi di atas EF sudah terisi sebagian dan di
bawah EF menjadi kosong sebagian.
Model elektron bebas terkuantisasi mengambil andaian sebagai berikut.
a. Kristal logam digambarkan sebagai superposisi dari jajaran gugus ion positip (yang
membentuk kisi kristal) dan elektron bebas yang bergerak dalam volume kristal.
b. Elektron bebas tersebut memenuhi kaidah fisika kuantum, yaitu mempunyai energi
terkuantisasi dan mematuhi larangan Pauli, yang secara menyatu dirangkum dalam
ungkapan rapat elektron
dn = n(E) dE = f(E) g(E) dE (3.28)
Dengan mensubstitusikan (3.27) dan (3.26) diperoleh ungkapan rapat elektron
sebagai fungsi dari energi elektron dan suhu sistem
3/ 2
1 ⎛ 2mo ⎞ E1/ 2
dn = ⎜ ⎟ dE (3.29)
2π 2 ⎝ 2 ⎠ 1 + e ( E − EF ) / kT
c. Pengaruh medan ion positip dapat diabaikan karena energi kinetik elektron bebas
sangat besar.
d. Pada permukaan batas antara logam dan vakum yang mengelilinginya terdapat
suatu potensial penghalang φ yang harus diloncati oleh elektron bebas paling
energetik pada suhu T=0 K (energi EF) untuk dapat meninggalkan permukaan
batas logam.

3.2.1 Sumbangan Elektron Bebas pada Harga CV
Rapat elektron pada suhu T=0 K
E 3/ 2 3/ 2
∞ ∞ Fo 1 ⎛ 2m ⎞ 1 ⎛ 2mo E F (0) ⎞
n = ∫ n( E )dE = ∫ f ( E ) g ( E )dE = ∫ ⎜ o ⎟ E 1 / 2 dE = ⎜ ⎟ (3.30)
2 ⎜ 2 ⎟ 2⎜ 2 ⎟
0 0 0 2π ⎝ ⎠ 3π ⎝ ⎠



dan rapat energi pada suhu T=0 K
E 3/ 2 3/ 2
∞ ∞ Fo 1 ⎛ 2m ⎞ 1 ⎛ 2m o ⎞
U o = ∫ Edn = ∫ Ef ( E ) g ( E )dE = ∫ E ⎜ o ⎟ E 1 / 2 dE = ⎜ ⎟ E F / 2 (0) (3.31)
5

⎜ 2 ⎟ 2⎜ 2 ⎟
0 0 0 2π 2 ⎝ ⎠ 5π ⎝ ⎠

Bila dinyatakan dalam rapat elektron (3.30) di atas, maka
3
Uo = nE F (0) (3.32)
5
Sedangkan rapat energi elektron pada suhu T>0 K
∞ ∞ 3/ 2
1 1 ⎛ 2mo ⎞
U = ∫ Ef ( E ) g ( E )dE = ∫ E ( E − E F ) / kT ⎜ ⎟ E 1 / 2 dE
0 0 1+ e 2π 2 ⎝ 2 ⎠
3/ 2 ∞
(3.32)
1 ⎛ 2mo ⎞ E 3/ 2
= ⎜ ⎟
2π 2 ⎝ 2 ⎠ ∫ 1 + e (E − EF ) / kT dE
o

Untuk menyelesaikan integral dalam (3.32) digunakan bentuk integral
∞
yj
F j ( yo ) = ∫ dy
o 1 + e ( y − yo )

yang mempunyai bentuk asymtotik untuk yo besar dan berharga positip
y oj +1 ⎛ π 2 j ( j + 1) ⎞
F j ( yo ) ≅ ⎜1 + + ... ⎟ (3.33)
j +1⎝ ⎜ 6 yo 2 ⎟
⎠
Diketahui bahwa ungkapan energi Fermi sebagai fungsi suhu adalah
⎛
E F = E F (0)⎜1 −
(π kT )2 ⎞
⎟ (3.34)
⎜ 12 E 2 (0) ⎟
⎝ F ⎠
Karena bentuk [(π kT ) 2 / E F (0)] sangat kecil dibandingkan dengan satu, maka EF
2

selalu dapat diganti dengan EF(0). Dengan memakai bentuk (3.33), (3.34) dan deret
binomial (1+x)p, serta memperhatikan ungkapan (3.31) dan (3.30), maka rapat energi
(3.32) di atas dapat dihitung dan hasilnya adalah
nπ 2 k 2T 2
U ≅ Uo + (3.35)
4EF
sehingga kapasitas panas elektron bebas



nπ 2 k 2T
(CV )el = ∂U / ∂T = (3.36)
2EF

Apabila kapasitas panas elektron bebas model klasik (CV )el (persamaan (3.13)),
'

maka ungkapan (3.36) untuk satu mol zat menjadi
π 2 kT
(CV ) el = (CV ) 'el (3.37)
3E F
Tampak bahwa sumbangan elektron bebas pada harga CV untuk kristal diperkecil
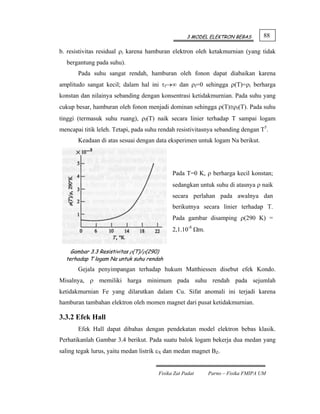
dengan faktor [π2kT/3EF] dari harga klasiknya. Untuk harga EF=5 eV dan T=300 K,
maka hal ini sesuai dengan hasil pengukuran bahwa faktor pengecil tersebut kira-kira
berorde 10-2.
Dapatlah disimpulkan bahwa sumbangan elektron bebas pada harga CV suatu
logam sangatlah kecil, terutama pada suhu yang sangat tinggi. Tetapi sumbangan
tersebut akan dominan pada suhu yang cukup rendah.
Pada suhu jauh di bawah suhu Debye θD dan suhu Fermi TF, kapasitas panas
suatu logam dapat ditulis sebagai jumlah sumbangan elektron bebas dan fonon, yakni
CV = γ T + A T3 (3.38)
dimana γ dan A merupakan konstanta karakteristik bahan. Secara eksperimen dapat
dibuat grafik CV/T terhadap T2 sehingga γ dan A bisa ditentukan.

3.2.2 Paramagnetik Pauli
Apabila terdapat suatu medan magnet luar H, maka spin elektron bebas akan
menyesuaikan diri terhadap H. Energi total elektron bebas karena pengaruh medan
Etot = Ekin ± μB μo H (3.39)
Tanda positip untuk spin antiparalel dan negatip untuk spin paralel terhadap medan.
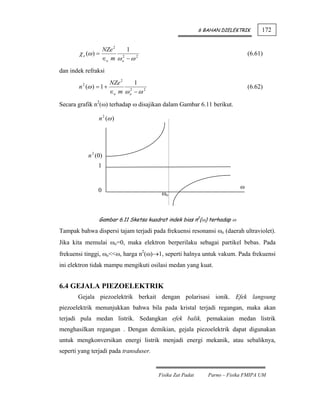
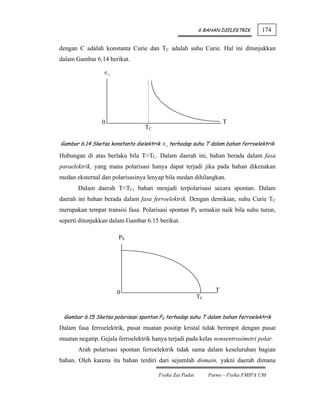
Pengaruh medan terhadap rapat keadaan g(E) digambarkan di bawah ini. Rapat
keadaan g(E) dibagi menjadi dua bagian, yaitu spin ke atas dan ke bawah. Tanpa
medan magnet luar H, keduanya simetris terhadap sumbu E.
Bila terdapat medan magnet luar H, maka secara total lebih banyak elektron
yang antiparalel terhadap H. Magnetisasi yang terjadi adalah



g(E) g(E)
μBμoH H

Ekin Ekin+mag

Gambar 3.1 Variasi tingkat energi karena aplikasi medan magnet luar H
∞ ∞
M = μ B ∫ dn =μ B ∫ f ( E ){1 g ( E + μ B μ o H ) − 1 g ( E − μ B μ o H )}
2 2 dE (3.40)
0 0

Bila diambil kasus untuk T=0 K, maka diperoleh
μ o μ B 3n
2
M = H (3.41)
2 E Fo

Perhitungan di atas menggunakan relasi g(E±μoμBH)=g(E)±μoμBH(dg/dE)
berdasarkan ekspansi Taylor; dan g(EF)=3n/2 EF yang diperoleh dengan
menggabungkan persamaan (3.26) dan (3.30). Dengan demikian suseptibilitas
magnetiknya
μ o μ B 3n
2
χ= (3.42)
2 E Fo
Terlihat bahwa suseptibilitas di atas tidak bergantung secara kuat terhadap suhu.
Dengan harga EFo=2 eV didapatkan χ=5.10-6 yang sesuai dengan hasil eksperimen.
Meskipun perhitungan di atas diambil pada suhu nol mutlak, tetapi hasilnya valid
dalam rentang suhu yang cukup besar.

3.2.3 Konduktivitas Listrik dalam Logam
Elektron yang mempunyai mobilitas besar untuk pindah ke keadaan elektron
yang lain adalah elektron yang berenergi E sedemikian sehingga f(E)<1. Hal ini
terjadi di daerah E∼EF. Elektron yang demikian akan mengalir bila dikenai medan
listrik. Hubungan rapat arus J dan medan listrik ε dinyatakan oleh hukum Ohm



J =σε (3.43)
dimana σ adalah konduktivitas listrik. Bila rapat elektron n dan kecepatan hanyut
elektron vd, maka rapat arus dapat juga diungkapkan dalam bentuk
J = n e vd
Dalam kesetimbangan termal, distribusi elektron berada dalam keadaan
mapan (steady state) no (v ) , yang tidak bergantung waktu. Dalam ruang kecepatan,

distribusi no (v ) mempunyai simetri bola, dan dinamakan bola Fermi (dengan radius

laju Fermi vF), serta permukaannya disebut permukaan Fermi. Kecepatan elektron
bersifat acak, dan berkaitan dengan energi melalui ungkapan
E = ½ m v2
direpresentasikan oleh semua titik dalam bola. Arus total nol karena setiap elektron
yang berkecepatan v selalu berpasangan dengan yang berkecepatan –v. Kecepatan
elektron sangat besar di permukaan Fermi. Permukaan Fermi tidak begitu dipengaruhi
oleh suhu. Bila suhu naik, hanya sedikit elektron yang melintasinya.
Perlu diketahui bahwa pengukuran eksperimen menunjukkan bahwa
permukaan Fermi berbentuk bola terdistorsi, sebagai akibat dilibatkannya interaksi
elektron dan kisi. Hal ini akan dijelaskan dalam bab selanjutnya.
Bila terdapat medan listrik, misalnya, εX searah sumbu-X, maka distribusi
elektron berubah menjadi n(v ) . Perubahan ini mempunyai komponen posisi dan
waktu. Dalam hal ini bola Fermi bergeser ke arah (-X), seperti ditunjukkan oleh
Gambar 3.2 berikut.



Gambar 3.2 a. Bola Fermi saat setimbang
b. Pergeseran bola Fermi saat dikenakan medan
Diambil asumsi bahwa kecepatan pergeseran titik pusat oleh kehadiran medan luar ini
sangat kecil bila dibandingkan dengan vrms.
Bila ε homogen (besar dan arahnya), maka perubahan distribusi elektron
hanya dipengaruhi oleh komponen waktu. Proses yang terjadi adalah adanya
perubahan distribusi elektron karena pengaruh medan luar ε dan adanya proses
hamburan yang ingin memulihkannya ke keadaan semula. Penggabungan kedua
proses ini menghasilkan persamaan kontinuitas
∂n(v ) eε n ( v ) − n o (v )
+ • ∇ V n(v ) + =0 (3.44)
∂t mo τ
dengan τ adalah waktu relaksasi. Ungkapan ini sering disebut persamaan transport
Boltzmann. Dalam keadaan mapan ( ∂n(v ) / ∂t = 0 ) persamaan (3.44) menjadi
τe
n(v ) = n o (v ) − ε • ∇ V n(v ) (3.45)
mo
ˆ
Dalam kasus di atas diambil ε = ε X i sehingga persamaan (3.45) menjadi

τ e ε X ∂n(v )
n(v ) = n o (v ) − (3.46)
mo ∂v X
Rapat arus listrik yang terjadi

J X = ∫ ev X n(v )dv X dv y dv z
∞
⎡ τ e ε X ∂n(v ) ⎤ (3.47)
=∫ ∫∞∫ ev X ⎢no (v ) − mo ∂v X ⎥dv X dv y dv z
− ⎣ ⎦
Integral suku pertama persamaan (3.47) menghasilkan nol karena kecepatan rata-rata
v X = 0 dalam no (v ) . Dengan demikian rapat arus (3.47) menjadi
∞
e 2ε X ∂n(v )
JX =−
mo ∫ ∫∫v
−∞
X
∂v X
dv X dv y dv z (3.48)

Mengingat bahwa
a. τ= /v, dimana adalah lintas bebas rata-rata antara dua tumbukan,



b. v 2 = v X + vY + v Z , dan
2 2 2

c. gerak elektron secara acak sehingga v X = 1 v 2
2
3

maka ungkapan rapat arus 3.48) berubah menjadi
∞
4πe 2 ε X ∂no (v )
JX = −
3mo ∫ 0
v
∂v
dv (3.49)

Dari rapat elektron (3.29), setelah mengganti variabel E menjadi v , diperoleh
distribusi elektron no (v ) tidak lain adalah
3
⎛m ⎞
no (v ) = 2⎜ o ⎟ f ( E ) (3.50)
⎝ h ⎠
Substitusi persamaan (3.50) dan setelah diadakan perubahan variabel v menjadi E,
maka rapat arus (3.49) menjadi
∞
16πe 2 mo ⎛ ∂f ( E ) ⎞
JX = ε X ∫ E⎜ − ⎟dE (3.51)
3h 0 ⎝ ∂E ⎠

Dengan demikian, mengingat hubungan (3.43) diperoleh konduktivitas listrik
∞
16πe 2 mo ⎛ ∂f ( E ) ⎞
σ=
3h ∫
0
E⎜ −
⎝ ∂E ⎠
⎟dE (3.52)

Untuk suhu T=0 K, harga (-∂f(E)/∂E) berupa fungsi delta Dirac δ sehingga integral
dalam (3.52)
∞
⎛ ∂f ( E ) ⎞
∫
0
E⎜ −
⎝ ∂E ⎠
⎟dE = EF EF

dan dengan menggunakan ungkapan rapat elektron (3.30), maka ungkapan
konduktivitas listrik (3.52) di atas menjadi
ne 2 ne 2τ F
σ= =
EF
(3.53)
mo v E F mo

dimana τF adalah waktu relaksasi sebuah elektron pada bola Fermi. Ungkapan
konduktivitas listrik di atas, ternyata, bentuknya sama dengan hasil teori Drude yang
lalu.



Baik teori Drude maupun model elektron bebas terkuantisasi mengemukakan
bahwa konduktivitas listrik hanya berbanding lurus dengan konsentrasi elektron.
Namun beberapa logam dengan konsentrasi elektron lebih tinggi, justru menunjukkan
nilai konduktivitas lebih rendah. Disamping itu, sebenarnya fakta menunjukkan
nahwa konduktivitas listrik bergantung pada suhu, dan juga arah.

3.3 PERILAKU ELEKTRON DALAM LOGAM

3.3.1 Hukum Matthiessen
Konduktivitas listrik logam bergantung pada suhu biasanya dibahas dalam
bentuk perilaku resistivitas ρ terhadap suhu T. diketahui bahwa ρ=σ--1 sehingga
berdasarkan konduktivitas (3.53), maka resistivitas dapat ditulis
m* 1
ρ= 2 (3.54)
ne τ
Elektron mengalami suatu tumbukan hanya karena ketidaksempurnaan
keteraturan kisi. Ketidaksempurnaan tersebut dapat berupa (a) vibrasi kisi (fonon)
dari ion di sekitar titik setimbang karena eksitasi termalnya, dan (b) semua
ketidaksempurnaan statik, seperti ketidakmurnian atau cacat kristal. Jika mekanisme
keduanya dianggap saling bebas satu sama lain, maka dapatlah diungkapkan
1/τ = 1/τf + 1/τi (3.55)
dimana suku pertama ruas kanan disebabkan oleh fonon dan suku kedua oleh
ketakmurnian. Dengan demikian, substitusi (3.55) ke dalam (3.34) menghasilkan
ungkapan resistivitas
m* 1 m* 1
ρ (T ) = ρ f (T ) + ρ i = + 2 (3.56)
ne 2 τ f ne τ i

Ungkapan ini disebut hukum Matthiessen. Tampak bahwa ρ terdiri dari dua bentuk,
yaitu
a. resistivitas ideal ρf(T) karena hamburan elektron oleh fonon, sehingga bergantung
pada suhu, dan



b. resistivitas residual ρi karena hamburan elektron oleh ketakmurnian (yang tidak
bergantung pada suhu).
Pada suhu sangat rendah, hamburan oleh fonon dapat diabaikan karena
amplitudo sangat kecil; dalam hal ini τf→∞ dan ρf=0 sehingga ρ(T)=ρi berharga
konstan dan nilainya sebanding dengan konsentrasi ketidakmurnian. Pada suhu yang
cukup besar, hamburan oleh fonon menjadi dominan sehingga ρ(T)≅ρf(T). Pada suhu
tinggi (termasuk suhu ruang), ρf(T) naik secara linier terhadap T sampai logam
mencapai titik leleh. Tetapi, pada suhu rendah resistivitasnya sebanding dengan T5.
Keadaan di atas sesuai dengan data eksperimen untuk logam Na berikut.

Pada T=0 K, ρ berharga kecil konstan;
sedangkan untuk suhu di atasnya ρ naik
secara perlahan pada awalnya dan
berikutnya secara linier terhadap T.
Pada gambar disamping ρ(290 K) =
2,1.10-8 Ωm.

Gambar 3.3 Resistivitas ρ(T)/ρ(290)
terhadap T logam Na untuk suhu rendah
Gejala penyimpangan terhadap hukum Matthiessen disebut efek Kondo.
Misalnya, ρ memiliki harga minimum pada suhu rendah pada sejumlah
ketidakmurnian Fe yang dilarutkan dalam Cu. Sifat anomali ini terjadi karena
hamburan tambahan elektron oleh momen magnet dari pusat ketidakmurnian.

3.3.2 Efek Hall
Efek Hall dapat dibahas dengan pendekatan model elektron bebas klasik.
Perhatikanlah Gambar 3.4 berikut. Pada suatu balok logam bekerja dua medan yang
saling tegak lurus, yaitu medan listrik εX dan medan magnet BZ.



Arus IX mengalir searah εX. akibat pengaruh medan BZ, lintasan elektron
membelok ke bawah, sehingga terkumpul banyak elektron di bagian bawah logam.
Dalam waktu bersamaan, terjadi muatan positip di bagian atas karena kekurangan
elektron. Dengan demikian terjadilah medan listrik Hall εY. apabila keadaan sudah
stasioner, maka εY konstan dan elektron bergerak dalam arah vX.

Y εx
Z + + + + + + +
εy
X - - - - - - -
vx=kec elektron
Bz

Gambar 3.4 Efek Hall
Dalam keadaan setimbang resultan gaya yang bekerja pada elektron (gaya
Coulomb dan Lorentz) sama dengan nol
eε Y − ev X BZ = 0 → ε Y = v X BZ
rapat arus dalam arah εX
JX = - n e vX
sehingga diperoleh harga konstanta Hall
εY 1
RH = =− (3.57)
J X BZ ne

Dengan mengukur εY, JX dan BZ, maka rapat elektron konduksi n dapat ditentukan.

Efek Hall dapat dipergunakan untuk menentukan
a. macam rapat pembawa muatan (positip atau negatip), dan
b. rapat elektron konduksi yang berperan dalam proses penghantaran muatan.

Ungkapan koefisien Hall di atas menunjukkan nahwa RH berharga negatip dan
hanya bergantung pada rapat elektron. Hasil percobaan menunjukkan bahwa pada
suhu kamar logam-logam Li, Na, Cu, Ag, dan Au berturut-turut memiliki konstanta
Hall –1,7.10-10, –2,5.10-10, –0,55.10-10, –0,84.10-10, dan –0,72.10-10 volt.m3/A.



Tetapi fakta lain menunjukkan bahwa terdapat beberapa logam mempunyai
RH positip, dan bahwa RH, umumnya, bergantung pada suhu, waktu relaksasi dan
besar medan magnet. Misalnya, logam Zn, dan Cd, masing-masing memiliki
konstanta Hall sebesar +0,3.10-10, dan +0,6.10-10 volt.m3/A. Hal ini menunjukkan
bahwa pembawa muatan dalam keduanya adalah lubang (hole).

Mobilitas elektron μ didefinisikan sebagai besarnya kecepatan rambat
elektron persatuan medan listrik μ=v/ε. Dari rapat arus J=nev=neμε sehingga dapat
dibentuk hubungan
1
− σ RH = neμ =μ (3.58)
ne
Jadi secara eksperimen dengan mengukur konduktivitas listrik σ dan koefisien Hall
RH, maka mobilitas elektron μ dapat ditentukan.
3.3.3 Resonansi Siklotron
Perhatikanlah Gambar 3.5 berikut.

B

sinyal
elektromagnet

Gambar 3.5 Gerakan siklotron
Medan magnet menyebabkan elektron bergerak melingkar berlawanan arah jarum
jam dalam bidang normal medan. Frekuensi gerak siklotron yang terjadi
eB
ωC = (3.59)
m*



Jika sinyal elektromagnet diarahkan tegak lurus B, maka elektron menyerap
energinya. Kecepatan absorbsi terbesar terjadi saat frekuensi sinyal benar-benar sama
dengan frekuensi siklotron
ω = ωC (3.60)
Masing-masing elektron bergerak sempurna sepanjang lingkaran sehingga absorbsi
terjadi secara kontinu sepanjang lintasan. Kondisi ini disebut resonansi siklotron. Jika
ω ≠ ωC, maka absorbsi sinyal hanya terjadi pada sebagian gerak elektron. Agar
gerakan elektron tetap melingkar, maka elektron harus mengembalikan energi yang
telah diserapnya. Bentuk kurva absorbsi ditunjukkan dalam Gambar 3.6 berikut.

α

ω
ωc

Gambar 3.6 Sketsa koefisien absorbsi terhadap frekunsi

Dari kurva absorbsi dapat diperoleh frekuensi siklotron ωC. Dengan demikian massa
elektron m* dapat diukur.

3.3.4 Pancaran Thermionik
Model elektron bebas terkuantisasi memiliki skema tingkat energi berikut.

elektron

eφ

EF

Gambar 3.7 Pancaran thermionik



Pada T=0 K semua tingkatan terisi sampai tingkat energi Fermi EF. Di atas tingkat EF
terdapat tingkat energi penghalang eφ sampai permukaan, yang dikenal sebagai
fungsi kerja logam. Dengan demikian untuk dapat meninggalkan logam, misalkan
dalam arah-X, elektron harus memiliki energi
2
pX
≥ E F + eφ (3.61)
2mo
Dalam statistik Fermi-Dirac, rapat elektron yang berkecepatan antara
(vX,vY,vZ) sampai (vX+dvX, vY+dvY, vZ+dvZ) adalah sama dengan ungkapan distribusi
(3.50), yaitu

( )
−1
⎛ mo ⎞ ⎛ ⎡ m v 2 + vY + v Z ⎤ ⎞
3 2 2
n(v X , vY , v Z ) dv X dvY dv Z = 2⎜ ⎟ ⎜1 + eksp ⎢ o X ⎥ ⎟ dv X dvY dv Z (3.62)
⎝ h ⎠ ⎜ ⎝ ⎣ 2kT ⎦⎠
⎟

Pancaran thermionik hanya mungkin terjadi pada energi yang sangat tinggi, sehingga
angka satu dalam penyebut persamaan (3.62) di atas dapat diabaikan. Oleh karena itu
distribusi rapat elektron (3.62) menjadi
− o (v X + vY + vZ )
3
⎛m ⎞
m2 2 2

n(v X , vY , v Z ) dv X dvY dv Z = 2⎜ o ⎟ e EF / kT e kT dv X dvY dv Z (3.63)
⎝ h ⎠
Rapat elektron dalam arah-X yang berkecepatan antara vX dan (vX+dvX)
⎛∞ ⎞
n(v X ) dv X = ⎜ ∫ ∫ n(v X , vY , v Z )dvY dv Z ⎟dv X
⎜ ⎟
⎝ −∞ ⎠ (3.64)
4π mo kT EF / kT − 2 kT v 2
2 o m

=
X

3
e e dv X
h
Untuk dapat meninggalkan batas permukaan, berdasarkan ungkapan (3.61) elektron
harus memiliki kecepatan awal minimal
2 E F + 2eφ
vX = (3.65)
mo

Disamping itu, pada permukaan batas kemingkinan terjadi proses pemantulan
kembali sebanyak r. Oleh karena itu rapat arus total dalam arah-X



∞
4π mo kT
2 m
− o v2
JX = (1 − r )e EF / kT ∫ ev X e 2 kT dv X
X

3
h vX (3.66)
= A(1 − r )T 2 e −eφ / kT
dengan A=(4πmok2e)/(h3)=1,2.106 Amp/m2 K2. Ungkapan ini dikenal sebagai
persamaan Richardson-Dushman untuk pancaran thermionik. Jika persamaan di atas
ditulis dalam bentuk logaritma-natural
ln (JX/T2) = ln A + ln (1-r) - eφ/kT
maka dengan membuat grafik ln(JX/T2) terhadap 1/T akan diperoleh harga φ dan (1-r).
Harga fungsi kerja beberapa logam yang diperoleh dari pengukuran emisi termionik
adalah 4,5; 4,2; 4,6; 4,8; 1,8; dan 5,3 eV, masing-masing untuk W, Ta, Ni, Ag, Cs
dan Pt.
Secara eksperimental pancaran thermionik ini dilakukan dalam tabung hampa,
dimana terdapat anoda yang mengumpulkan elektron yang dipancarkan oleh katoda.

3.4 KEBERATAN TERHADAP MODEL ELEKTRON BEBAS
TERKUANTISASI
Gejala fisis yang diprediksi oleh model elektron bebas, ternyata, ada yang
menyimpang dari data pengamatan. Kelemahan ini telah dikemukakan secara singkat
dalam masing-masing bahasannya, yaitu antara lain sebagai berikut.
a. Konduktivitas listrik yang hanya bergantung pada konsentrasi elektron. Padahal
fakta menunjukkan bahwa logam divalent (Be, Cd, Zn, dan lain-lain), dan bahkan
logam trivalent (Al, dan In) memiliki konduktivitas lebih rendah daripada logam
monovalen (Cu, Ag, dan Au) meskipun konsentrasi elektron lebih banyak.
b. Koefisien Hall selalu berharga negatip. Padahal beberapa logam menunjukkan
konstanta Hall positip, seperti Be, Zn, dan Cd.
c. Permukaan Fermi mempunyai simetri bola. Padahal pengukuran kadang-kadang
menunjukkan permukaan Fermi berbentuk non-simetri bola.
Model elektron bebas mengandaikan elektron berada dalam kotak potensial
sederhana V(x) yang sama untuk seluruh logam (biasanya V(x)=0), dan hanya pada



permukaan batas ada potensial penghalang φ yang menghindarkan semua elektron
bebas untuk meninggalkan permukaan logam. Dengan pengandaian ini, maka
interaksi antara elektron dan ion dianggap sebagai benturan mekanis elastik. Tidak
ada interaksi listrik antara ion dan elektron, karena interaksi ini telah termaksud
dalam potensial V(x)=tetap di atas.
Model pengandaian benturan elastik di atas, memberikan suatu nilai (lintas

bebas rata-rata) yang panjang dibandingkan dengan jarak rata-rata antarion dalam
kristal logam. Hal inilah yang, barangkali, menyebabkan bahasan “aliran” elektron
dalam logam kurang bisa memprediksi kenyataan.

RINGKASAN
01. Logam mengandung elektron bebas (konduksi), dengan konsentrasi besar, yang
dapat bergerak dalam keseluruhan volume kristal. Jika ρm dan ZV, masing-masing
adalah kerapatan bahan dan valensi atom, maka konsentrasi elektron bebas
ρm N A
tersebut adalah n = Z V
M
02. Teori Drude (1900) tentang elektron dalam logam adalah bahwa dalam logam
terdapat elektron bebas, yang membentuk sistem gas elektron klasik, yang
bergerak acak dalam kristal dengan kecepatan random vo karena energi termal dan
berubah arah geraknya setelah bertumbukan dengan ion logam. Karena massanya
yang jauh lebih besar, maka ion logam tidak terpengaruh dalam tumbukan ini.
e 2 nτ
Teori Drude menghasilkan ungkapan konduktivitas listrik σ = dan termal
mo

3 nk 2Tτ
K= . Hal lain yang didapat adalah bahwa konsentrasi elektron
2 mo



berbanding terbalik dengan akar suhu mutlak n ∼ T-1/2. Ungkapan terakhir ini tidak
sesuai dengan fakta, dan menyebabkan teori Drude tidak memadai.
03. Model elektron bebasa klasik tentang logam mengambil andaian bahwa elektron
bebas diperlakukan sebagai gas, yang masing-masing bergerak secara acak dengan
kecepatan termal, pengaruh medan potensial ion diabaikan, karena energi kinetik
elektron bebas sangat besar, dan lektron hanya bergerak dalam kristal karena
adanya penghalang potensial di permukaan batas. Teori ini gagal menerangkan
kapasitas panas sumbangan elektron bebas pada suhu tinggi dan Suseptibilitas
magnetik.
04. Model elektron bebas yang terkuantisasi menggunakan prinsip kuantisasi energi
elektron dan prinsip eksklusi Pauli, pengaruh medan ion positip dapat diabaikan
karena energi kinetik elektron bebas sangat besar dan pada permukaan batas antara
logam dan vakum yang mengelilinginya terdapat suatu potensial penghalang φ
yang harus diloncati oleh elektron bebas paling energetik pada suhu T=0 K (energi
EF) untuk dapat meninggalkan permukaan batas logam.
05. Menurut model elektron bebas yang terkuantisasi, ungkapan kapasitas panas
nπ 2 k 2T
elektron bebas adalah (CV )el = yang sesuai dengan hasil eksperimen.
2E F

μ o μ B 3n
2
Sedangkan untuk suseptibilitas magnetik diperoleh χ = yang cocok juga
2 E Fo
dengan hasil eksperimen. Model ini juga menghasilkan ungkapan konduktivitas
listrik yang sama dengan yang diperoleh teori Drude.
06. Hukum Matthiessen membahas resistivitas elektron dalam logam dikarenakan
dua hal, yaitu hamburan elektron oleh fonon (bergantung pada suhu) dan oleh
ketakmurnian (tidak bergantung pada suhu). Pada suhu sangat rendah, hamburan
oleh fonon dapat diabaikan. Sedangkan pada suhu yang cukup besar, hamburan
oleh fonon menjadi dominan.
07. Efek Hall dapat dipergunakan untuk menentukan macam rapat pembawa muatan
(positip atau negatip), dan rapat elektron konduksi yang berperan dalam proses



penghantaran muatan. Eksperimen efek Hall menggunakan sampel yang dialirkan
arus dan medan magnet secara tegak lurus. Karena adanya gaya Coulomb dan
Lorentz, maka pada keadaan kesetimbangan terjadi beda potensial Hall.
08. Resonansi siklotron digunakan untuk mencari massa efektif elektron. Pada sampel
dikenakan sinyal elektromagnet dan medan magnet B, yang saling tegak lurus.
Elektron menyerap energi gelombang elektromagnet. Kecepatan absorbsi terbesar
terjadi saat frekuensi sinyal benar-benar sama dengan frekuensi siklotron.
09. Pancaran thermionik adalah gejala keluarnya arus elektron dari bahan karena
suhu. Kegunaan pancaran thermionik adalah untuk menentukan fungsi kerja logam
dan koefisien pantul elektron pada permukaan bahan.
10.Gejala fisis yang diprediksi oleh model elektron bebas, yang menyimpang dari
data pengamatan, antara lain konduktivitas listrik yang hanya bergantung pada
konsentrasi elektron, koefisien Hall selalu berharga negatip, dan permukaan Fermi
mempunyai simetri bola. Penyimpangan ini akan diperbaiki oleh bahasan teori Pita
Energi, bab selanjutnya, yaitu manakala potensial inti berpengaruh terhadap
perilaku elektron konduksi.

LATIHAN SOAL BAB III
01. Jelaskan perbedaan antara elektron terlokalisasi dan terdelokalisasi dalam
padatan!
02. Tembaga memiliki kerapatan massa ρm=8,95 gr/cm3 dan resistivitas listrik
ρ=1,55.10-8 Ωm pada suhu kamar. Jika diasumsikan massa efektif m*=mo, maka
hitunglah
a. konsentrasi elektron konduksi n!
b. waktu bebas rata-rata τ!
c. energi Fermi EF!
d. suhu Fermi TF!
e. kecepatan Fermi vF!



f. jalan bebas rata-rata pada tingkat Fermi F!

g. persentase elektron yang mengalami eksitasi di atas tingkat Fermi pada suhu
kamar!
03. Natrium memiliki koefisien ekspansi volume 15.10-5/K. Hitunglah persentase
perubahan energi Fermi EF jika suhu dinaikkan dari 0 K sampai 300 K!
04. Tembaga mempunyai suhu Einstein θE=240 K. Dengan menggunakan harga
energi Fermi soal 02), hitunglah perbandingan kapasitas panas elektron terhadap
kisi pada suhu T=0,3 K, T=4 K, T=20 K, T=77 K dan T=300 K!
05. Anggaplah bahwa energi Fermi EF=5 eV dan tidak bergantung suhu. Berapakah
harga energi untuk fungsi Fermi-Dirac f(E)=0,5 , f(E)=0,7 , f(E)=0,9 dan
f(E)=0,95 pada suhu kamar!
06.a. Buktikan bahwa kapasitas panas kisi dan elektronik berharga sama pada suhu

5θ D
3
TC = !
24π 2TF

b. Hitunglah suhu soal a) untuk logam Ag yang mempunyai suhu Debye θD=225 K
dan suhu Fermi TF=6,4.104 K!
c. Tunjukkan bahwa pada suhu T<TC kapasitas panas elektronik lebih besar
daripada kapasitas panas kisi; dan sebaliknya pada T>TC!
07. Jika padatan natrium mempunyai energi Fermi EF=3,12 eV, maka berapakah
suseptibilitas paramagnet Paulinya?
08. Tembaga mempunyai konstanta Hall RH=-0,55.10-10 Vm3/A. Hitunglah
konsentrasi elektronnya!
09. Dalam suatu sampel tembaga didapati kecepatan hanyut elektron 2,16 m/s dalam
medan listrik 500 V/m. Hitunglah
a. mobilitas elektron!
b. waktu relaksasi (anggaplah m*=mo)!



10. Resistivitas listrik suatu sampel tembaga adalah 1,77.10-8 Ωm. Tembaga
berstruktur FCC dengan sisi kubus 3,61 Å dan masing-masing atom
menyumbangkan satu elektron bebas. Tentukanlah
a. waktu relaksasi!
b. kecepatan rata-rata elektron dalam medan 100 V/m!
11. Logam emas mempunyai kerapatan massa 19,3.103 kg/m3. Jika masing-masing
atomnya menyumbangkan satu elektron untuk menghasilkan arus, maka hitunglah
koefisien Hall dalam logam tersebut!
12. Pengamatan resonansi siklotron dalam tembaga terjadi pada frekuensi 24 GHz.
Jika untuk tembaga m*=mo, maka hitunglah medan magnet yang digunakan!
13. Sesium mempunyai fungsi kerja 1,8 eV. Hitunglah rapat arus emisi thermionik
pada suhu 500 K, 1000 K, 1500 K dan 2000 K! (anggaplah tidak ada elektron yang
terpantul di permukaan)
14.a. Buktikan bahwa emisi thermionik mencapai maksimum bila suhu T=eφ/2k!
b. Berapakah suhu soal a) untuk logam Cs dengan fungsi kerja 1,8 eV?


B A B IV
ELEKTRON DALAM LOGAM II
(TEORI PITA ENERGI)

Bahasan gerakan elektron dalam logam dengan menggunakan model elektron
bebas, seperti bab sebelumnya, adalah terlalu sederhana karena potensial kristal tidak
diperhitungkan. Model elektron bebas tidak bisa menjelaskan beberapa gejala fisis,
seperti membedakan antara logam, semilogam, semikonduktor dan isolator; koefisien
Hall berharaga positip; hubungan elektron konduksi dalam logam dengan elektron
valensi atom bebas; dan berbagai gejala transport. Oleh karena itu, bab ini menelaah
pengaruh potensial kristal terhadap elektron dalam padatan.
Bagian awal bab ini menyajikan teori pita energi secara agak rinci. Perilaku
elektron dalam pengaruh potensial periodik kristal memenuhi teorema Bloch.
Bahasan teori ini menunjukkan bahwa spektrum energi merupakan pita kontinu. Hal
ini berbeda dengan spektrum energi atom yang bersifat diskrit. Di antara pita energi
terdapat celah energi yang merupakan daerah terlarang bagi perilaku gelombang
elektron. Disamping itu, teori ini mampu menunjukkan perbedaan antara logam dan
isolator.
Elektron dalam kristal selalu dalam keadaan bergerak. Berdasarkan ungkapan
energi, maka dapat dibahas kecepatan dan massa efektif elektron. Juga, dibahas
pengaruh medan listrik pada gerakan elektron sehingga menghasilkan rumusan
konduktivitas listrik elektron yang lebih umum. Apabila pengaruh medan potensial
kristal terhadap elektron diabaikan, maka rumusan konduktivitas umum ini dapat
direduksi menjadi konduktivitas seperti bab yang lalu.
Akhirnya, bab ini menyajikan perilaku elektron dalam medan magnet.
Bahasan ini mencakup efek Hall dan resonansi siklotron.

4 TEORI PITA ENERGI 99

4.1 TEORI PITA ENERGI UNTUK ZAT PADAT
Apabila deretan ion tersusun teratur dan membentuk kisi kristal, maka energi
potensial kristalnya berubah secara periodik sesuai dengan periodisitas kisi tersebut.
“Dilihat” oleh elektron, potensial kristal tersebut seperti disajikan pada Gambar 4.1
berikut.

Gambar 4.1 Potensial sebagai fungsi jarak sepanjang garis inti atom
Elektron yang dapat bergerak bebas di antara ion adalah elektron yang berada di atas
potensial penghalang.
Teori pita energi zat padat mengajukan model tentang elektron dalam kristal
dengan asumsi sebagai berikut.
a. Terdapat energi potensial V (r ) yang tidak sama dengan nol di dalam kristal
dengan keberkalaan kisi kristal.
b. Fungsi gelombang ψ (r ) dibuat berdasarkan kisi sempurna dan dimana dianggap
bahwa kisi tidak bervibrasi secara termal.
c. Teori pita energi dikembangkan dari bahasan perilaku elektron tunggal di bawah
pengaruh suatu potensial periodik V (r ) yang merepresentasikan semua interaksi,
baik dengan ion kristal maupun dengan sesama elektron lain.
d. Bahasan elektron tunggal dapat menggunakan persamaan Schrodinger untuk satu
elektron
2
− ∇ 2ψ (r ) + V (r )ψ (r ) = Eψ (r ) (4.1)
2mo
dengan ketentuan bahwa pengisian keadaan elektron yang diperoleh menganut
distribusi Fermi-Dirac.



4.1.1 Teorema Bloch
Menurut Bloch, persamaan Schrodinger untuk suatu potensial dengan
periodisitas translasi kisi
( )
V r + R = V (r ) (4.2)

dimana R adalah vektor kisi, mempunyai solusi berbentuk

ψ k ( r ) = u k ( r ) e ik • r (4.3)

dengan u k (r ) merupakan suatu fungsi yang juga mempunyai simetri translasi kisi

( )
u k r + R = u k (r ) (4.4)
Fungsi Bloch merupakan gelombang bidang berjalan yang dimodulasi oleh medan
potensial periodic, dan ungkapan teorema Bloch, yaitu
“Fungsi eigen dari persamaan gelombang untuk suatu potensial periodik
adalah hasilkali antara suatu gelombang bidang berjalan eksp (ik • r ) dan
suatu fungsi modulasi u k (r ) dengan periodisitas kisi kristal”

Fungsi Bloch ψ (r ) merupakan orbital kristal, yakni bersifat delokalisasi di seluruh
volume kristal. Kemampuan elektron bergerak dalam keseluruhan kristal ditandai
oleh adanya bentuk gelombang bidang berjalan eksp (ik • r ) dalam fungsi Bloch
sehingga seperti partikel bebas. Sedangkan gerakan elektron di sekitar inti
2
dideskripsikan oleh fungsi periodic. Distribusi probabilitas elektron ψ (r ) bersifat

periodik dalam kristal.
Misalnya, kisi kristal satu dimensi dalam arah-X dengan perioda a, maka
dapatlah dikemukakan beberapa hal sebagai berikut.
a. Mengingat V(x+a)=V(x), maka disamping ψ(x), juga ψ(x+a) merupakan solusi
persamaan Schrodinger dengan energi E. Apabila tidak ada degenerasi, maka
terdapat hubungan
2π
ika k= n , n = 0,1,2,3,...
ψ(x+a) = e ψ(x) dimana Na (4.5)
N = titik kisi identik



b. Mengingat V(x) riil, maka V*(x)=V(x). Karenanya setiap E senantiasa ada dua
fungsi gelombang yang memenuhi persamaan Schrodinger, yaitu ψ*(x) dan ψ(x);
dan E(k)=E(-k).
c. Mengingat hubungan antara vektor kisi resiprok G dan periodisitas kisi a adalah
G a = m 2π ; m = 0, ±1, ±2, …
maka suatu keadaan elektron dengan vektor gelombang G memenuhi
ψG(x+a) = ψG(x) (4.6)

Sedangkan suatu keadaan elektron dengan vektor gelombang k ' = G + k
memenuhi
ψ k ' ( x + a ) = e ikaψ k ' ( x) (4.7)

Hal ini berarti ψ k ' ( x) memenuhi teorema Bloch seolah-olah dengan vektor

gelombang k. Dengan demikian suatu keadaan elektron tertentu mempunyai
vektor gelombang tidak unik. Mengingat hubungan
2π
k'= G + k = m+k
a
⎛ π⎞ ⎛π ⎞
maka kita bataskan saja daerah ⎜ − ⎟ ≤ k ≤ ⎜ ⎟ . Ternyata semua harga k yang
⎝ a⎠ ⎝a⎠
lain dapat dikembalikan ke dalam daerah tersebut, sehingga daerah ini disebur
Zona Brillouin Pertama.

4.1.2 Model Kronig-Penney
Model Kronig-Penney menelaah gerak elektron dalam suatu potensial persegi
periodik, seperti Gambar 4.2 berikut.

V(x)
ion

Vo

x
-b 0 a a+b 2a+b 2a+2b

Gambar 4.2 Potensial persegi periodik yang dikenalkan Kronig-Penney



Terlihat bahwa perioda potensial sebesar (a+b) dan
⎧ 0 , untuk 0 < x < a
V =⎨
⎩V0 , untuk − b < x < 0
Oleh karena itu persamaan Schrodinger yang sesuai
2
d2
− ψ ( x) = Eψ ( x) , untuk 0 < x < a (4.8)
2m0 dx 2
2
d2
− ψ ( x) + Voψ ( x) = Eψ ( x) , untuk − b < x < 0 (4.9)
2m0 dx 2
Jika kita bataskan E<Vo dan dua besaran riil
2mo E
α2 = 2
(4.10)

2mo (Vo − E )
β2 = 2
(4.11)

maka solusi persamaan di atas adalah
untuk 0<x<a, ψ = Ae iαx + Be − iαx (4.12)

untuk –b<x<0, ψ = Ce βx + De − βx (4.13)
Solusi sempurna, yakni yang memenuhi fungsi Bloch (4.3), didapatkan dengan
merelasikan solusi untuk a<x<(a+b) dan –b<x<0 dengan teorema Bloch
ψ(a<x<(a+b)) = ψ(-b<x<0) eik(a+b) (4.14)
Tetapan A, B, C dan D dipilih sedemikian sehingga ψ dan dψ/dt kontinu di
x=0 dan x=a. Syarat batas di x=0 menghasilkan
A+B=C+D (4.15)
i α (A – B) = β (C – D) (4.16)
dan syarat batas di x=a menghasilkan
A eiαa + B e-iαa = (C e-βb + D eβb) eik(a+b) (4.17)
iα (A eiαa - B e-iαa = β (C e-βb - D eβb) eik(a+b) (4.18)
Perangkat empat persamaan (4.15) sampai (4.18) di atas memberikan solusi hanya
jika determinan dari koefisien A, B, C dan D sama dengan nol. Hal ini menghasilkan



β 2 −α 2
sinh (β b )sin (α a ) + cosh (β b ) cos(α a ) = cos k (a + b ) (4.19a)
2αβ
Hasil di atas menjadi lebih sederhana apabila potensial periodik merupakan fungsi
delta Dirac, yakni Vo→∞ dan b→0, tetapi Vob→berhingga. Dalam kasus ini β>>α
dan βb<<1 sehingga persamaan (4.19a) di atas menjadi
⎛ moVo b ⎞
⎜ 2 ⎟ sin (α a ) + cos(α a ) = cos ka (4.19b)
⎝ α ⎠

⎛m V b⎞
Apabila dibataskan P = ⎜ o 2o ⎟ , maka persamaan (4.19b) menjadi
⎝ ⎠

sin (α a ) + cos(α a ) = cos ka
P
(4.19c)
αa
Secara grafik, untuk P=3π/2 persamaan ini dapat digambarkan dalam sketsa berikut.

sin (α a ) + cos(α a ) = cos ka untuk P=3π/2
P
Gambar 4.3 Sketsa fungsi
αa
= daerah αa yang meberikan solusi persamaan
Schrodinger

Tampak bahwa nilai energi E yang diperkenankan, dalam ungkapan
1/ 2
⎛ 2mo E ⎞
αa=⎜ 2
⎟ a , untuk fungsi (4.19c) di atas, terletak antara ±1. Sedangkan
⎝ ⎠
daerah lain, yang tidak mengandung solusi, merupakan harga energi yang terlarang.



Secara singkat dari gambar di atas dapatlah dikemukakan hal-hal berikut.

a. Spektrum energi elektron terdiri dari beberapa pita energi (daerah energi) yang
diperkenankan dan beberapa yang terlarang.
b. Lebar pita energi yang diperkenankan bertambah lebar dengan meningkatnya
harga αa, atau dengan energi elektron yang meningkat.
c. Lebar pita energi tertentu yang diperkenankan mengecil apabila P bertambah,
artinya mengecil bila “energi ikatan” makin naik.

Apabila P→∞, maka persamaan (4.19c) mempunyai solusi hanya bila
Sin αa = 0
αa = ± n π, dengan n = ±1, ±2, ±3, …
Oleh karena itu berdasarkan persamaan (4.10) diperoleh harga energi
2
α2 π2 2
E= = 2
n2 (4.20)
2mo 2mo a
Ungkapan (4.20) ini sama dengan energi elektron dalam kotak potensial. Energi
elektron bersifat diskrit.

Apabila P→0, maka persamaan (4.19c) haruslah memenuhi
Cos αa = cos (ka)
α=k
sehingga berdasarkan persamaan (4.10) diperoleh harga energi
2
k2
E= (4.21)
2mo
Ungkapan (4.21) ini sama dengan energi elektron bebas. Energi elektron bersifat
kontinu.

d. Ketidaksinambungan dalam lengkung E=E(k) terjadi pada harga
cos (ka) = ±1 atau k= nπ/a, dengan n = ±1, ±2, ±3, …



Berikut disajikan gambar sketsa energi E untuk berbagai harga P.
a. P = 0 (elektron bebas)

V(x) E(k)

0 x k
0

b. 0<P<∞ (elektron dalam potensial berkala)

V(x) E(k)

Vo

x k
-3π/a -2π/a -π/a 0 π/a 2π/a 3π/a

c. P=∞ (elektron terikat)

V(x) ∞
∞ ∞ ∞ ∞ E3

E2
E1
x

Gambar 4.4 Sketsa energi E terhadap berbagai harga P
Dapatlah disimpulkan bahwa pola harga energi elektron untuk sistem potensial
berkala adalah keadaan antara model elektron bebas dan kotak potensial.

4.1.3 Pita Energi dan Energi Elektron dalam Atom
Dalam suatu susunan atom terisolasi, kumpulan atom di dalamnya
mempunyai jarak antaratom yang tidak berhingga besarnya. Energi elektron dalam



setiap atom bersifat diskrit, dan sesungguhnya atom dalam keseluruhannya bukanlah
merupakan suatu sistem fisis. Tingkat energi atom yang diskrit tersebut dinamakan
tingkat 1s, 2s, 2p dan seterusnya. Setiap atom merupakan sistem tersendiri, tanpa
interaksi dengan atom lain. Atom yang terisolasi ini, masing-masing memiliki
banyak keadaan elektron yang sama energinya.
Apabila kemudian jarak antaratom berkurang, maka mulai terjadi interaksi
antaratom dan fungsi gelombang elektron mulai saling bertindihan. Interaksi tersebut
menyebabkan harga energinya berubah. Secara keseluruhan atom tersusun menjadi
satu sistem fisis dan harus mengikuti kaidah yang menyangkut sistem fisis. Misalnya,
prinsip Pauli yang melarang dua elektron atau lebih mempunyai harga energi yang
tepat sama. Oleh karena itu terjadi pelebaran dari harga diskrit energi elektron (atom
terisolasi) menjadi harga pita energi elektron.
Berdasarkan prinsip larangan, tiap tingkat energi tersedia bagi dua elektron
dengan spin berlawanan. Oleh karena itu pita energi suatu zat padat yang terdiri dari
N atom akan tersedia N tingkat energi atau paling banyak boleh berisikan 2N
elektron. Karena N besar sekali, yakni 1023, maka tingkat-tingkat energi tersebut
saling merapat satu sama lain membentuk pita energi. Pita energi terdiri dari
kumpulan tingkat energi yang memiliki jarak antartingkat berdekatan sangat kecil
sehingga distribusinya kontinu. Misalnya, lebar pita energi 5 eV memiliki jarak
antartingkat berdekatan 5.10-23 eV. Jadi pada suatu kristal terdapat banyak pita energi
yang masing-masing sesuai dengan tingkat energi atom penyusun kisi tersebut.
Misalnya, tingkat energi 1s, 2s, dan 2p masing-masing menimbulkan pita 1s, 2s, dan
2p.
Perhatikanlah contoh kristal Lithium dalam gambar berikut. Setiap atom Li
mengandung tiga elektron, yaitu 2 elektron mengisi sel 2s dan 1 elektron dalam sel
2s (tidak penuh). Pita 2s dan 2p masing-masing mempunyai kapasitas 2N dan 6N
elektron. Terlihat bahwa lebar pita bertambah saat konstanta kisi mengecil. Juga,
untuk a<6ao (dimana ao adalah radius Bohr seharga 0,53 Å) pelebaran pita 2s dan 2p
mulai overlap, dan celah antara keduanya melenyap sehingga terbentuk pita tunggal
dengan kapasitas 8N. Tetapi pita tunggal ini hanya berisikan N elektron yang berasal


dari pita 2s saja, atau hanya seperdelapan dari kapasitasnya. Karena pita valensinya
hanya terisi sebagian, maka kristal Li termasuk kelompok logam.

Gambar 4.5 Pelebaran tingkat energi 2s dan 2p menjadi pita energi dalam kristal
Pita-pita energi memang berkecenderungan overlap satu sama lain. Selain
pita 2s dan 2p seperti di atas, pita yang berkecenderungan overlap adalah 3s dan 3p
yang berkapasitas 8N; 4s, 3d dan 4p yang berkapasitas 18N; 5s, 4d dan 5p yang
berkapasitas 18N; 6s, 4f, 5d dan 6p yang berkapasitas 32N; serta 7s, 5f, 6d dan7p
yang berkapasitas 32N. Sebagai contoh berikut disajikan unsur wolfram (W).
Dalam sistem periodik unsur W termasuk golongan VIA dan memiliki nomor
atom 74 dengan konfigurasi elektron [Xe]4f145d46s2. Hal ini berarti semua elektron
sudah memiliki spin yang sudah berpasang-pasangan sehingga tidak ada yang
menjadi elektron bebas. Tetapi, faktanya tidak demikian. Wolfram termasuk
konduktor yang baik. Ternyata, antara satu pita energi dengan yang lain
dimungkinkan terjadi tumpang-tindih. Untuk konduktor W tersebut, tumpang tindih
terluar terjadi pada pita energi 6s, 4f, 5d dan 6p yang secara total memerlukan 32
elektron. Sedangkan, di luar sel [Xe], wolfram hanya memiliki 20 elektron. Hal ini
berarti masih terdapat 12 tempat kosong elektron, yang bisa berperan sebagai hole.
Meskipun pada dasarnya bentuk solusi fungsi gelombang menuruti teorema
Bloch, namun dalam memecahkan persamaan Schrodinger, dengan pendekatan



tentang model potensial berkala, memberikan berbagai metode, antara lain sebagai
berikut.
a. Metode LCAO (linear combination of atomic orbitals), dimana spektrum energi
elektron dalam zat padat diperoleh dengan mengandaikan adanya sedikit
tumpang-tindih dari potensial atom yang terpisah. Potensial atom yang begitu kuat
menyebabkan elektron hanya bergerak di sekitar atom yang bersangkutan. Model
ini merupakan pendekatan kasar terhadap pita sebelah dalam, yaitu pita 3d logam
transisi.
b. Model elektron hampir bebas, dimana diandaikan bahwa potensial berkala agak
rendah; atau dimana tumpang-tindih dari potensial atom sangat besar. Karena
potensial begitu lemah, maka elektron berperilaku seperti elektron bebas dan
model ini dibahas dengan metode perturbasi. Model ini merupakan pendekatan
kasar terhadap pita valensi logam sederhana, seperti Na, K, Al dan lain-lain.
c. Metode sel (cellular method) yang dikembangkan oleh Wigner-Seitz.
Dalam buku ini hanya akan disajikan metode LCAO saja.

4.1.4 Refleksi Bragg dan Celah Energi
Bahasan moda getar kisi kristal linier diatomik yang lalu menunjukkan bahwa
pada batas zona (k=±π/2a) besar kecepatan kelompok vg=0, baik pada cabang akustik
maupun optik, sehingga pada titik ini terjadi gelombang tegak. Kondisi ini
menimbulkan refleksi Bragg.
Gerakan elektron dalam potensial berkala model Kronig-Penney
menunjukkan bahwa celah energi terjadi pada harga k=nπ/a, dimana n=±1, ±2, …
Pada harga batas inipun, fungsi Bloch merupakan gelombang tegak. Gerakan
elektron dalam kisi dapat dianalogikan dengan propagasi gelombang elektromagnet
dalam kristal. Jika k dan k ' , masing-masing adalah merupakan vektor gelombang
asal dan terhambur, dan G adalah vektor kisi resiprok, maka syarat difraksi Bragg
harus memenuhi (1.37), yaitu
k ' = Ghkl + k



Karena k ' = k , maka syarat Bragg menjadi

G • G + 2k • G = 0
Untuk kristal monoatomik linier dengan jarak antaratom a, hal ini menjadi
G π
k =± =± (4.22)
2 a
Pada saat kondisi (4.22) terpenuhi, gelombang yang merambat ke kanan mengalami
refleksi Bragg ke kiri, dan sebaliknya. Oleh karena itu terjadilah gelombang yang
tidak merambat ke kanan maupun ke kiri. Gelombang ini disebut gelombang tegak.
Dalam hal ini ungkapan gelombang tegak dapat berbentuk
⎧ iπ x π
−i x ⎫ πx
ψ genap ( x) = u genap ( x)⎨e + e a ⎬ = 2u genap ( x) cos
a
(4.23)
⎩ ⎭ a

Rapat muatan listriknya
2 πx
− eψ genap ( x) = −e 2u genap ( x) cos 2
a
yang berharga maksimum pada setiap saat x=am, dimana m adalah bilangan bulat;
jadi pada setiap lokasi atom dalam kristal. Disamping itu, gelombang tegak
termaksud di atas dapat pula disusun dari dua fungsi ganjil
π π
⎧ i x −i x ⎫ πx
ψ ganjil ( x) = u ganjil ( x)⎨e a
−e a
⎬ = 2iu ganjil ( x) sin (4.24)
⎩ ⎭ a

Rapat muatan listriknya
2 πx
− eψ ganjil ( x) = −e 2iu ganjil ( x) sin 2
a
yang berharga nol pada setiap lokasi atom dalam kristal linier. Oleh karena itu
elektron dengan harga k=±π/a dapat direpresentasikan sebagai
a. fungsi gelombang yang selama sebagian besar dari waktunya berada di dekat inti
atom (x=ma), atau
b. fungsi gelombang yang selama sebagian besar dari waktunya berada dalam ruang
di antara inti atom (jauh dari inti atom).



Dari Gambar 4.1 dan 4.2 terlihat bahwa energi potensial elektron di dekat inti atom
lebih rendah daripada di dalam ruang antara inti atom. Oleh karena itu energi yang
diperlukan untuk elektron yang direpresentasikan oleh ψgenap(x) lebih rendah
daripada untuk elektron yang direpresentasikan oleh ψganjil(x). Beda energi elektron
antara keduanya pada batas k==±π/a ini merupakan celah energi.

4.1.5 Logam, Isolator dan Semikonduktor
Daerah energi yang diperkenankan sesungguhnya merupakan keadaan
elektron yang tersedia bagi elektron dalam kristal. Terisi atau tidak terisi keadaan
elektron tersebut oleh elektron masih bergantung pada jumlah dan statistika elektron
dalam kristal.
Ada dua hal, dimana medan listrik luar tidak menghasilkan arus elektron
dalam kristal, yaitu
a. pita energi yang diperkenankan sama sekali tidak dihuni elektron, dan
b. pita energi yang diperkenankan terisi penuh oleh elektron, atau semua keadaan
elektron terisi penuh oleh elektron.
Hal pertama mudah dipahami, yakni karena tidak ada elektron dalam pita energi,
maka arus elektronpun sama dengan nol. Hal kedua, misalnya kuat medan listrik ε
berpengaruh pada distribusi kecepatan elektron v . Andaikanlah kecepatan masing-
masing elektron adalah vi , maka kecepatan rata-rata untuk elektron dengan

kerapatan no pada volume kristal V adalah
1
v=
noV
∑v
i
i (4.25)

Penjumlahan dilakukan terhadap semua elektron dalam pita yang ditinjau. Rapat arus
elektron yang terjadi
e
J = −no ev = −
V
∑v
i
i (4.26)

Misalnya, pita yang ditinjau seperti Gambar 4.6 berikut.



E(k)

k
-π/a 0 π/a

Gambar 4.6 Pita energi yang diperkenankan

Dalam hubungannya dengan frekuensi radial ω, energi elektron dapat dinyatakan
E= ω (4.27)

sehingga kecepatan kelompok vg dapat dinyatakan
dω 1 dE
vg = = (4.28)
dk dk
Pada gambar di atas, vg sama dengan kemiringan fungsi E=E(k). Sedangkan fungsi
E=E(k) simetri terhadap sumbu k=0. Pada harga k=-k, kecepatan elektron sama
besar, tetapi berlawanan tanda, sehingga ∑vi=0. Dengan demikian, jelaslah bahwa
rapat arus sama dengan nol untuk suatu pita energi yang kosong (elektron) atau pita
energi yang penuh.
Hanya pita energi yang terisi sebagian (atau yang kosong sebagian) dapat
memberikan sumbangan pada arus listrik. Misalnya, sebuah elektron A berada
dalam suatu pita energi yang kosong, seperti Gambar 4.7 berikut.

E(k)

A’ A”

A
k
-π/a 0 π/a

Gambar 4.7 Sebuah elektron dalam suatu pita energi kosong



Posisi setimbang elektron berada pada kedudukan paling rendah. Medan listrik ε
menyebabkan gaya sebesar -eε bekerja pada elektron, dan menggerakkannya secara
terus-menerus ke arah keadaan elektron dengan momentum linier (negatip) yang
makin besar sampai akhirnya mencapai titik A’ pada posisi k=-π/a. Pada titik ini
terjadi refleksi Bragg, dan elektron muncul di titik A” pada posisi k=+π/a; dan
kemudian menempuh lagi siklus yang sama. Proses pengulangan ini disebut osilasi
Zener. Adanya ketidaksempurnaan kisi menyebabkan hamburan terjadi sebelum
osilasi Zener sempat muncul.
Misalnya, dalam pita yang ditinjau terdapat keadaan elektron total sebanyak
, yang terisi elektron sebanyak i, dan yang kosong sebanyak s. Jika masing-masing

dianggap mempunyai distribusi kecepatan, maka

∑ v =∑ v + ∑ v
i
i
s
s (4.29)

karena ∑v =0 , yakni semua keadaan elektron dianggap terisi penuh eleh elektron,

maka rapat arus elektron dapat dinyatakan seperti halnya persamaan (4.26), yakni
e
J =−
V
∑v i
i (4.30)

dan dapat juga ditulis dalam bentuk
e
J =+
V
∑v s
s (4.31)

ungkapan rapat arus (4.30) menunjukkan bahwa pembawa muatannya adalah
elektron yang bermuatan –e. Umumnya, ungkapan ini digunakan bila keadaan
elektron di pita energi yang diperkenankan hanya terisi elektron sedikit saja, seperti
Gambar 4.8 berikut.



E(k)

k
-π/a 0 π/a

Gambar 4.8 Pita energi yang diperkenankan dengan sedikit elektron di dalamnya
Ungkapan rapat arus (4.31) menunjukkan bahwa pembawa muatannya mempunyai
muatan +e (sering disebut hole) dan “menempati” keadaan elektron yang kosong.
Umumnya, ungkapan ini digunakan bila pita energinya hampir penuh elektron. Hole
menempati pita energi bagian atas, seperti Gambar 4.9 berikut.

E(k)

k
-π/a 0 π/a

Gambar 4.9 Pita energi yang diperkenankan dengan hole pada bagian atasnya
Berdasarkan uraian tentang pengisian keadaan elektron dalam pita energi
yang diperkenankan seperti di atas, dapatlah dibedakan antara konduktor, isolator,
semikonduktor dan semilogam.

Isolator. Semua energi terisi penuh oleh elektron atau sama sekali kosong, sehingga
tidak dapat terjadi konduksi listrik. Pita energi tertinggi yang terisi penuh elektron
disebut pita valensi. Celah energi ΔE cukup besar, sehingga elektron dari pita energi



EF ΔE

Gambar 4.10 Pengisian elektron dalam pita energi bahan isolator
: pita energi terisi elektron
: pita energi kosong

yang penuh tidak dapat melompat (karena energi termal) ke pita energi yang kosong.
Tingkat energi Fermi EF melalui daerah energi yang kosong. Contoh isolator adalah
intan (karbon) yang memiliki celah energi 6 eV. Hal ini dijelaskan oleh Gambar 4.10
di atas.

Konduktor. Tingkat energi Fermi EF melewati pita energi yang diperkenankan,
sehingga pita tersebut setengahnya (atau sebagiannya) terisi oleh elektron. Pita energi
tertinggi yang terisi elektron sebagian disebut pita konduksi. Ada sebagian elektron
di atas EF (apabila T>0 K), tetapi masih berada dalam daerah pita energi yang sama,
dengan meninggalkan keadaan elektron kosong (hole) di bawah EF. Konduksi listrik
terutama terjadi aliran elektron. Contoh konduktor adalah logam alkali (Li, K dan
lain-lain) dan logam mulia (Cu, Ag, Au dan lain-lain). Hal ini dijelaskan dalam
Gambar 4.11 berikut.



EF

ΔE

Gambar 4.11 Pengisian elektron dalam pita energi bahan konduktor
: hole
: elektron yang melompati EF

Semikonduktor. Tingkat energi Fermi EF melewati daerah harga energi terlarang,
sehingga pada T=0 K hanya ada pita yang sama sekali penuh, dan di atasnya pita
energi yang kosong sama sekali. Celah energi ΔE tidak tinggi, sehingga pada T>0 K
sebagian elektron dapat melompatinya, dan berpindah ke pita konduksi yang masih
kosong. Sementara tempat yang ditinggalkan elektron menjadi hole dalam pita
valensi. Dengan demikian, pembawa muatannya adalah elektron dan hole. Makin
tinggi suhu, makin banyak elektron yang melampaui ΔE sehingga konduktivitas zat
makin meningkat. Contoh semikonduktor adalah Si dan Ge, dengan celah energi
masing-masing 1,1 eV dan 0,7 eV. Umumnya, pada suhu kamar celah energi
semikonduktor kurang dari 2 eV. Sketsa pengisian elektron dalam pita energi

EF ΔE

Gambar 4.12 Pengisian elektron dalam pita energi bahan semikonduktor



Semilogam. Celah energi lenyap seluruhnya, atau bahkan kedua pita energi terjadi
overlap tipis. Contoh semilogam adalag Bi, As, Sb dan Sn putih.

4.1.6 Metode LCAO
Dalam menghitung tingkat energi elektron dalam kristal, metode LCAO
menganggap bahwa elektron terikat kuat pada atom. Metode LCAO termasuk
pendekatan ikatan kuat (“tight binding approximation”). Energi potensial elektron
merupakan bagian yang dominan dari energi totalnya, sedangkan harga energi
elektron yang diperkenankan merupakan pita sempit bila dibandingkan dengan
daerah harga yang tidak diperkenankan. Fungsi gelombang elektron didasarkan pada
fungsi gelombang elektron dalam atom yang terisolasi, dan disusun dari fungsi
gelombang elektron termaksud. Pendekatan ini berbeda dengan pendekatan elektron
bebas.
Misalnya, orbital masing-masing atom adalah ψo. Bila sejumlah atom
tersusun menjadi susunan kristal dengan potensial periodik, tetapi sedemikian rupa
sehingga ψo tidak terlalu banyak dipengaruhinya, maka fungsi gelombang elektron di
dalam kristal secara keseluruhan dapat ditulis sebagai kombinasi linier dari seluruh
fungsi gelombang atom dalam kristal

ψ k (r ) = ∑ e ik •r ψ o (r − rn )
n
(4.32)
n

Penjumlahan dilakukan atas semua posisi atom rn dalam kristal. Bila potensial

periodik kristal V (r ) dan potensial atom terisolasi di r=rn adalah Vo (r − rn ) , maka

persamaan Schrodinger dapat ditulis
H ψ k (r ) = E ψ k (r ) (4.33)

dengan Hamiltonian
2
H =− ∇ 2 + V (r )
2mo
⎧ 2
⎫
= ⎨− ∇ 2 + Vo (r − rn )⎬ + { (r ) − Vo (r − rn )}
V (4.34)
⎩ 2mo ⎭
= Ho + H'



dengan demikian Ho adalah Hamiltonian untuk sebuah atom terisolasi di r=rn, dan H’
untuk semua atom lainnya. Harga ekspektasi energi diperoleh dari
1
N∫
E = ψ k (r ) Eψ k (r )dτ
*

(4.35)
1 1
= ∫ψ k (r ) H oψ k (r )dτ + ∫ψ k (r ) H 'ψ k (r )dτ
* *

N N
Integral pertama dalam (4.35) adalah energi sebuah atom terisolasi Eo. Untuk
menghitung integral kedua, permasalahannya disederhanakan, yakni hanya
meperhitungkan interaksi antartetangga terdekat atom saja. Oleh karena itu integral
kedua dapat dipecah menjadi dua bagian, yakni yang hanya meliputi n=m saja dan
yang hanya meliputi interaksi antartetangga terdekat saja dengan indek j.
1
∫ψ k (r ) H 'ψ k (r )dτ
*

N
1
= ∑∑ e ik •( rn − rm ) ∫ψ o (r − rm ) H 'ψ o (r − rn )dτ
*

N n m
1
= ∑ ∫ψ o (r − rn ) H 'ψ o (r − rn )dτ + ∑ e n j ∫ψ o (r − r j ) H 'ψ o (r − rn )dτ
* ik • ( r − r ) *

N n j

≅ ∫ψ o (r − rn ) H 'ψ o (r − rn )dτ + ∑ e ∫ψ
ik •( rn − r j )
* *
o (r − r j ) H 'ψ o (r − rn )dτ
j

≅ −α − β ∑ e
ik •( rn − r j )

j

dengan batasan bahwa integral Coulomb

∫ψ (r − rn ) H 'ψ o (r − rn )dτ = −α
*
o (4.36)

dan integral overlap

∫ψ (r − r j ) H 'ψ o (r − rn )dτ = − β
*
o (4.37)

Dengan demikian energi elektron (4.35) dalam kristal di atas dapat ditulis

∑e
ik •( rn − r j )
E = Eo − α − β (4.38)
j

dengan r j = kedudukan atom di sekitar atom rn

α dan β = besaran positip, karena H’ negatip



Ungkapan energi (4.38) mengasumsikan bahwa orbital atom ψo mempunyai simetri
bola sehingga faktor overlap β berharga sama untuk semua pasangan tetangga
terdekat.
Dalam kisi kubik sederhana dengan rusuk a, setiap titik kisi mempunyai 6
tetangga terdekat, sehingga
(rn − r j ) = ± a x, ± a y, ± a z
ˆ ˆ ˆ

Oleh karena itu pita energinya
E(k) = Eo - α - 2β (cos kxa + cos kya + cos kza) (4.39a)
Persamaan (4.39a) dapat juga ditulis dalam bentuk
E(k) = Ev + 4β [sin2 (kxa/2) + sin2 (kya/2) + sin2 (kza/2)] (4.39b)
dimana Ev=Eo-α-2β merupakan energi dasar pita.
Dari ungkapan pita energi (4.39) ini dapatlah dikemukakan hal-hal berikut.
a. E(k) periodik terhadap k
b. E(k) = E(-k)
c. E(k)max = Eo - α + 6β dan E(k)min = Eo - α - 6β
E(k)max dan E(k)min, masing-masing adalah harga energi elektron pada puncak dan
dasar pita energi. Beda antara keduanya merupakan pita energi, yang besarnya
sebanding dengan integral overlap. Rentang energi dalam pita energi ini berperan
sebagai energi kinetik elektron, sehingga elektron mampu bergerak ke bagian
seluruh kristal.

d. Untuk harga k sangat kecil, yakni di dekat dasar pita energi elektron menjadi

E(k) ≅ Eo - α - 6β + β a2 k2 (4.40)
Terlihat bahwa harga energi ini sama dengan hubungan dispersi untuk elektron
bebas.
Gambar 4.13 berikut menyajikan kurva dispersi sepanjang arah [100] dan [111].



Gambar 4.13. Kurva dispersi sepanjang arah [100] dan [111]
untuk kisi kubik sederhana dalam model ikatan kuat
Model ikatan kuat di atas memperlihatkan bahwa setiap tingkatan energi
atomik meluas menjadi sebuah pita energi sebagai akibat adanya interaksi antaratom
dalam padatan. Setiap pita energi menggambarkan karakter tingkatan energi atom
mula-mula.
Energi tetap elektron dalam kisi kubik sederhana di atas dapat dibuat
konturnya. Untuk ka<<1, energi tersebut, yakni persamaan (4.40) dapat dinyatakan
sebagai
E (k ) Eo − α − 6 β
k x2 + k y + k z2 =
2
− = tetap
β a2 β a2
yang merupakan persamaan bola dalam ruang k. Sedangkan energi maksimum terjadi
apabila
cos kxa = cos kya = cos kza = -1
kx = ky = kz = ±π/a
Titik ini merupakan titik ujung Zona Brillouin Pertama. Bila dilihat dari titik ujung
(dekat E(k)max) dengan melakukan transformasi dari k ke k’=(π/a)-k, maka dengan
menggunakan persamaan (4.39b) didapatkan E(k’) – Emaks = - a2 β (k’)2, yakni
bentuk permukaan energi tetap juga merupakan bola dengan ujung Zona Brillouin
tersebut sebagai pusatnya. Dalam bidang kz=0, kontur energi elektron dalam kisi
kubik sederhana ditunjukkan oleh Gambar 4.14 berikut.



Gambar 4.14 Kontur energi kisi kubik sederhana dalam model ikatan kuat

4.2 DINAMIKA ELEKRON DALAM KRISTAL

4.2.1 Kecepatan Kelompok dan Massa Efektif Elektron dalam
Kristal
Gerak elektron dalam kristal dapat divisualisasikan sebagai suatu paket
gelombang yang merupakan superposisi gelombang dari berbagai frekuensi ω. Paket
gelombang ini mempunyai kecepatan kelompok sama seperti persamaan (4.28) yang
secara vektor dinyatakan oleh
v g = ∇ k ω (k ) (4.41a)

Karena energi elektron E= ω, maka

1
vg = ∇ k E (k ) (4.41b)

Simak kembali elektron yang hanya bergerak dalam arah sumbu-X dalam kisi
kubik sederhana, sehingga energi (3.39) dapat dinyatakan
E(kx) = Eo’ – 2 β cos kxa (4.42)
dengan Eo’ adalah konstanta. Kecepatan kelompok dalam arah-X
1 ∂E (k x ) 2 β a
(v g ) x = = sin k x a (4.43)
∂k x



Sketsa E(kx) dan (vg)x dalam (4.42) dan (4.43) di atas disajikan pada Gambar 4.15
berikut.

Gambar 4.15 a. Struktur pita energi kisi kubik sederhana arah-X
b. Kecepatan elektron dalam pita energi yang bersangkutan. Garis
putus-putus menunjukkan kecepatan elektron bebas
Terlihat bahwa di dekat pusat zona kecepatan elektron sebanding dengan vektor
gelombang. Di daerah ini elektron berperilaku seperti elektron bebas. Di dekat batas
zona, kecepatan elektron menurun drastis, dan akhirnya nol tepat pada batas zona. Di
titik ini terjadi gelombang tegak. Disamping itu, telah dijelaskan bahwa untuk pita
energi yang terisi penuh elektron tidak dapat menunjukkan arus listrik. Hal ini
terlihat pada gambar di atas bahwa
v ( − k ) = −v ( k )
sehingga kecepatan total elektron sama dengan nol.
Ungkapan (4.41b) menunjukkan bahwa kecepatan kelompok sebanding
dengan gradien energi. Hal ini berarti gerak elektron sangat ditentukan oleh
permukaan energi tetap. Apabila permukaan energi tetap tersebut berupa permukaan
bola (daerah dekat pusat zona), maka arah v g adalah radial. Di dekat batas zona,

kontur energi mengalami distorsi (dari permukaan bola) sehingga v g tidak radial.

Hal ini ditunjukkan oleh Gambar 4.16 berikut.


Gambar 4.16 Kecepatan elektron dan perubahan bentuk permukaan Fermi saat
konsentrasi elektron valensi atau konduksi meningkat
Bentuk permukaan Fermi ditentukan oleh geometri kontur energi dalam pita
energi karena sesungguhnya permukaan Fermi itu sendiri adalah sebuah kontur
energi dengan E(k)=EF pada T=0 K. Gambar 4.16 di atas juga menunjukkan
perubahan bentuk permukaan Fermi saat konsentrasi elektron valensi n meningkat.
Populasi n kecil hanya mengisi daerah dekat dasar pita pada pusat zona sehingga
volumenya berbentuk bola yang dibatasi oleh permukaan bola Fermi. Saat n naik,
“volume Fermi” mengembang, dan kontur energi mulai terdistorsi. Distorsi menjadi
besar saat permukaan Fermi memotong garis batas zona.
Perubahan kecepatan kelompok terhadap waktu t adalah
dv g 1 d
= ∇ k E (k ) (4.44a)
dt dt
Untuk suatu vektor A tertentu berlaku
dA dk
= (∇ k A) •
dt dt
Oleh karena itu
dv g 1 dk
= ∇ k (∇ k E ) • (4.44b)
dt dt
Gaya luar F pada elektron menyebabkan perubahan momentum
dk
F= (4.45)
dt
Substitusi dk / dt dari (4.45) ke dalam (4.44b) menghasilkan ungkapan percepatan



dv g 1
a= = 2
∇ k (∇ k E ) • F (4.46a)
dt
Dalam koordinat Kartesis, ungkapan percepatan (4.46a) ini berbentuk
1 ∂2E
ai = ∑ Fj dengan i, j = x, y, z (4.46b)
2
∂k i ∂k j

Hubungan ini analogi dengan hukum II Newton, sehingga massa efektif m*
didefinisikan sebagai
1 1
= 2 ∇ k (∇ k E ) (4.47a)
m*
atau dalam koordinat Kartesis
⎛ 1 ⎞ 1 ∂2E
⎜ ⎟ = 2 (4.47b)
⎝ m * ⎠ ij ∂k i ∂k j

Dari hubungan (4.47) di atas terlihat bahwa massa efektif adalah tensor rank-dua dan
simetrik
⎛ 1 ⎞ ⎛ 1 ⎞
⎜ ⎟ =⎜ ⎟ (4.48)
⎝ m * ⎠ ij ⎝ m * ⎠ ji
Massa efektif elektron m* tidak perlu sama dengan massa sesungguhnya mo. Hal ini
disebabkan oleh adanya dua gaya yang bekerja sekaligus pada elektron, yakni gaya
medan kristal (dalam penetapan E(k)) dan gaya luar F.
Elektron bebas dalam ruang mempunyai energi kinetik sama seperti
persamaan (3.24) , yang dapat dituliskan
2
E (k ) = (k x2 + k y + k z2 )
2
(4.49)
2mo
Menurut teori di atas diperoleh
⎛ 1 ⎞ 1 ∂2E 1 ⎛ 1 ⎞ 1 ∂2E
⎜ ⎟ = 2 = dan ⎜ ⎟ = 2 =0
⎝ m * ⎠ xx ∂k x ∂k x mo ⎝ m * ⎠ xy ∂k x ∂k y

Simetri ruang dimana elektron berada menyebabkan indek xx=yy=zz dan
xy=yz=zx=yx=xz=zy, sehingga



⎛1 / m o 0 0 ⎞
⎛ 1 ⎞ ⎜ ⎟
⎜ ⎟ =⎜ 0 1 / mo 0 ⎟ (4.50)
⎝ m * ⎠ xx ⎜
⎝ 0 0 1 / mo ⎟
⎠
Persamaan Newton yang dapat disusun
⎛ ax ⎞ ⎛ 1 0 0 ⎞⎛ Fx ⎞
⎜ ⎟ 1 ⎜ ⎟⎜ ⎟
⎜ay ⎟ = ⎜ 0 1 0 ⎟⎜ Fy ⎟ (4.51)
⎜ a ⎟ mo ⎜ 0 0 1 ⎟⎜ F ⎟
⎝ z⎠ ⎝ ⎠⎝ z ⎠
1
merupakan hubungan vektor a = F . Artinya arah percepatan a sesuai dengan
mo

arah gaya F . Jelas bahwa untuk elektron bebas berlaku m*=mo, karena tidak ada
gaya kisi yang bekerja pada elektron.

Untuk gerak elektron dalam suatu kristal kubik sederhana, khususnya bila k

sangat kecil terhadap 1/a, maka persamaan (4.40) dapat dituliskan
E (k ) = E o − α − 6 β + β a 2 (k x2 + k y + k z2 )
2
(4.52)

Dengan cara yang sama hasilnya terlihat bahwa tensor (1/m*) tidak nol hanya untuk
elemen diagonalnya, yakni masing-masing besarnya
2β a 2
2

Oleh karena itu massa efektifnya isotropik, dan dapat direpresentasikan dengan
skalar
2
1
m* = (4.53)
2a β
2

Terlihat bahwa dalam daerah ini elektron berperilaku seperti elektron bebas dengan
massa efektif yang berbanding terbalik dengan integral overlap β. Makin besar
overlap, makin mudah elektron menerobos dari satu atom ke atom yang lain sehingga
(massa) inersia elektron lebih kecil, dan sebaliknya. Dalam model ikatan kuat ini
overlap kecil sehingga massa efektif besar.
Di dekat puncak pita elektron memperlihatkan perilaku yang lain. Misalnya,
elektron dalam kisi kubik sederhana satu dimensi dalam arah-X. Jika didefinisikan


kx’=(π/a)-kx dan energi kinetik E(kx) persamaan (4.42) dideretkan dekat titik
maksimum, maka didapatkan
E(kx’) = Ex,max – a2 β(k’)2 (4.54)
Jadi elektron berperilaku seperti partikel bebas yang mempunyai massa efektif
negatip
2
1
m* = − (4.55)
2a β
2

Gambar 4.17 berikut menyajikan struktur pita dan massa efektif dalam kisi kubik
sederhana satu dimensi arah-X

Gambar 4.17 a. Struktur pita, dan b. Masa efektif elektron sebagai fungsi kx
dalam kisi kubik sederhana
Massa efektip negatip di daerah yang lebih besar dari titik perubahan kc, menandakan
adanya percepatan negatip elektron karena menurunnya kecepatan. Di daerah ini kisi
mengenakan gaya pemerlambat yang sangat besar pada elektron.

4.2.2 Pengaruh Medan Listrik pada Kecepatan Elektron dalam
Kristal
Pengaruh gaya luar F terhadap momentum elektron dalam kristal
diungkapkan oleh persamaan (4.45), yakni



dk
=F (4.56)
dt
Hal ini berarti vektor gelombang k terus meningkat terhadap naiknya waktu t,
seperti ditunjukkan dalam Gambar 4.18 berikut.

kx
π/a

t
0

-π/a

Gambar 4.18 Vektor gelombang elektron Bloch sebagai fungsi waktu saat dikenai gaya
luar F (satu dimensi)
Terlihat bahwa karena pengaruh Fx, momen kristal kx senantiasa meningkat sampai
mencapai batas Zona Brillouin Pertama. Pada saat itu terjadi UMKLAPP dan gerak
elektron mulai lagi dari batas baru zona.
Misalnya, medan luar εx menyebabkan gaya Fx=-eεx bekerja pada elektron,
sehingga vektor gelombang kx berubah terhadap waktu. Gerakan elektron dalam
“repeated-zone scheme”, disajikan dalam Gambar 4.19 berikut. Elektron bergerak
sepanjang lintasan OABC dan seterusnya. Sedangkan dalam “reduced-zone scheme”,
saat elektron sampai di batas zona A, kemudian segera muncul di titik ekivalensinya,
yaitu A’, sehingga terjadi gerakan elektron sepanjang OA(→A’)OA dan seterusnya.
Karena sifat simetri translasi, maka terlihat bahwa titik A, A’ dan C, C’ adalah
ekivalen; begitu pula O dan B.



Gambar 4.19 a.Gerakan sebuah elektron karena kehadiran medan listrik
b. Kecepatan elektron
Pada Gambar 4.19b di atas terlihat bahwa kecepatan elektron (mulai k=0)
meningkat mencapai maksimum, tetapi kemudian turun dan akhirnya nol pada batas
zona. Kemudian elektron berbalik sehingga mempunyai kecepatan negatip, begitu
seterusnya. Bahasan ini terjadi dalam ruang nyata, seperti ditunjukkan oleh Gambar
4.20 berikut.

t

D

C

B

A

0
xo

Gambar 4.20 Gerak elektron dalam ruang nyata-X sebagai fungsi waktu



Terlihat bahwa gerak elektron hanya bolak-balik antara x=0 sampi x=xo. Setiap kali
elektron berada di x=xo, energinya berada di puncak pita konduksi dimana kemudian
terjadi refleksi Bragg. Gerakan osilasi periodik elektron Bloch ini sangat berbeda
dengan perilaku elektron bebas.
Apabila εx cukup besar, maka dapat terjadi loncatan elektron ke pita di
atasnya, seperti ditunjukkan oleh Gambar 4.21 berikut. Apabila elektron di A dan
memperoleh energi sebesar celah energi ΔE, maka elektron tidak dipantulkan
kembali, tetapi mampu melompat ke pita energi di atasnya(titik A”). Misalnya, jarak
kedua titik AA” adalah d, maka haruslah
ΔE
d≤ (4.57)
eε x

E(k)

A”
ΔE
A

k
0 π/a 2π/a

Gambar 4.21 Gerakan elektron karena medan listrik yang melintasi celah energi
Hal ini dinamakan “tunneling”, dengan syarat bahwa d jauh lebih kecil dari panjang
gelombang de Broglie dan juga kecil terhadap konstanta kisi.

4.2.3 Konduktivitas Listrik
Dalam sistem setimbang, permukaan Fermi berpusat di titik asal. Akibatnya
arus netto nol, karena setiap elektron dalam keadaan k yang berkecepatan v (k )

selalu berpasangan dan saling menghapus dengan elektron di keadaan − k yang
berkecepatan v (−k ) = −v (k ) .



Bila dikenakan medan listrik εx, terjadi perpindahan δkx selama interval
waktu δt, yang memenuhi persamaan
eε x
δ kx = − δt (4.58a)

Karena elektron bertahan dalam interval waktu tumbukan τ, maka
eε x
δ kx = − τ (4.58b)

Akibatnya permukaan Fermi berpindah sejauh δkx, seperti ditunjukkan oleh Gambar
4.22 berikut.

Gambar 4.22 Permukaan Fermi: a. dalam keadaan setimbang,
dan b. dalam kehadiran medan listrik εx
Perpindahan menyebabkan terdapat beberapa elektron (dalam daerah bayang-
bayang) tidak mempunyai pasangan untuk menghapusnya, sehingga terjadi arus
netto. Pada T=0 K arus netto tersebut
⎛δE ⎞
J x = −ev F , x g ( E F )δ E = −ev F , x g ( E F )⎜
⎜δ k ⎟δ k x
⎟ (4.59)
⎝ x ⎠
dengan v F , x = kecepatan Fermi rata-rata dalam arah-X

g(EF)δE = konsentrasi elektron yang tidak berpasangan
g(EF) = rapat keadaan pada permukaan Fermi
δE = energi medan yang diserap elektron
Mengingat ∂E/∂kx= vF,x dan harga δkx dalam (4.58b) di atas, maka didapatkan

J x = e 2 v F , xτ F g ( E F )ε x
2
(4.60)



sehingga konduktivitas listrik
σ = e 2 v F , xτ F g ( E F )
2
(4.61)

Ungkapan (4.61) adalah bentuk umum konduktivitas listrik untuk suatu permukaan
Fermi tertentu. Tampak bahwa σ bergantung pada kecepatan Fermi vF dan waktu
tumbukan τF, serta pada rapat keadaan pada permukaan Fermi g(EF). Tingkat EF
suatu logam berada di tengah pita energi, dimana g(EF) besar, sehingga konduktivitas
besar. Sedangkan tingkat EF pada isolator berada pada puncak pita, dimana g(EF)=0,
sehingga konduktivitas nol, meskipun kecepatan Fermi sangat besar.
Permukaan Fermi sferik menyebabkan v F , x = 1 v F sehingga ungkapan (4.61)
2
3
2

menjadi σ = 1 e 2 vFτ F g (E F )
3
2
(4.62a)

Dengan menggunakan hubungan rapat keadaan (3.26) dan (3.30) untuk elektron
bebas, yakni
3/ 2
1 ⎛ 2m * ⎞ ⎛ 2 ⎞
g (E) = EF = m * v ⎜ 2m * ⎟(3π n)
EF = ⎜
/2 2 2 3/ 2
⎜ ⎟ E 1
⎟
2π 2 ⎝ 2 ⎠
F 2 F
⎝ ⎠
maka didapatkan ungkapan konduktivitas listrik (4.62a) menjadi
ne 2τ F
σ= (4.62b)
m*
yang hanya berlaku untuk model elektron bebas.

4.2.4 Dinamika Elektron dalam Medan Magnet
4.2.4.1 Efek Hall
Dalam logam terdapat hole dan elektron. Bila dua pita mengalami overlap
satu terhadap yang lain, maka elektron berada pada pita bagian atas dan hole di
bagian yang lebih rendah. Konstanta Hall saat elektron dan hole ada dalam waktu
bersamaan diungkapkan oleh
Reσ e2 + Rhσ h
2
R= (4.63)
(σ e + σ h )2
dimana Re = konstanta Hall untuk elektron
Rh = konstanta Hall untuk hole



σe = konduktivitas listrik elektron
σh = konduktivitas listrik hole
Jika konsentrasi elektron sama dengan hole, ne=nh, maka besarnya Re sama dengan
Rh, dan tanda R ditentukan oleh harga relatif konduktivitas σe terhadap σh. Harga
σe>σh berarti bahwa elektron memiliki massa lebih kecil dan waktu hidup panjang,
sehingga sumbangan elektron yang dominan dan R berharga negatip, dan sebaliknya.
Jika pembawa muatan hanya elektron, maka Rh dan σh berharga nol, sehingga
R=Re. Hal ini didapat pada model elektron bebas.
4.2.4.2 Resonansi Siklotron
Dinamika elektron dalam medan magnet diungkapkan oleh
dk
dt
(
= −e v ( k ) × B ) (4.64)

Momentum kristal berubah terhadap waktu karena kehadiran gaya Lorentz.
Perpindahan δ k dalam waktu δt dituliskan dalam bentuk

δk =−
e
(v (k ) × B )δ t (4.65)

Perpindahan δ k tegak lurus terhadap bidang yang dibentuk oleh v (k ) dan B .

Mengingat v adalah normal kontur energi dalam ruang k (Gambar 4.16), maka
berarti δk terjadi pada sepanjang kontur energi, seperti ditunjukkan oleh Gambar 4.23
berikut.



Gambar 4.23 Lintasan elektron sepanjang kontur energi
dalam ruang k karena adanya medan magnet
Karena elektron bergerak sepanjang kontur energi tetap, maka tidak terjadi
proses penyerapan energi terhadap medan magnet. Gerakan elektron yang demikian
bersifat siklis. Bila v normal terhadap B , maka gerak elektron mempunyai perioda
δk
T = ∫δ t =
eB ∫ v(k )
(4.66)

dimana integrasi dilakukan sepanjang orbit tertutup elektron dalam ruang k . Dengan
demikian, ungkapan umum frekuensi siklotron untuk elektron Bloch ini adalah
2π eB
ωc = (4.67)
δk
∫ v(k )
Eksperimen resonansi siklotron dilakukan dengan mendatangkan berkas
radiasi elektromagnetik pada daerah gelombang radio pada permukaan logam, yang
sebelumnya telah dikenakan medan magnet B dalam arah tegak lurus berkas
elektromagnetik, seperti disajikan oleh Gambar 4.24 berikut.

Gelombang radio

δ

Medan magnet

Gambar 4.24 Eksperimen resonansi siklotron

Radiasi elektromagnetik ini hanya mampu menembus sedalam “skin depth” δ pada
permukaan logam. Elektron menyerap energi sinyal elektromagnetik. Resonansi
terjadi antara gerak putar elektron karena B dan energi gelombang radio yang



diserapnya, serta elektron berada dalam daerah “skin depth”. Apabila frekuensi
gelombang radio ωo, maka
ωo = n ωc (4.68)
dengan n adalah bilangan bulat.
Apabila energi elektron mempunyai bentuk E=( 2k2/2m*), maka orbit

elektron berupa lingkaran, v(k ) = k / m * dan k keduanya besarnya konstan
sepanjang kontur energi. Oleh karena itu dari (4.67) diperoleh ungkapan frekuensi
eB
ωc =
m*
yang sama dengan yang diperoleh oleh model elektron bebas.
Resonansi siklotron, umumnya, digunakan untuk mengukur massa efektif
elektron. Umumnya, frekuensi ωo besarnya tertentu dan medan magnet divariasi
sehingga terjadi kondisi resonansi. Percobaan yang dilakukan oleh Azbel-Kaner
(untuk bahan Cu) menyajikan data impedansi riil permukaan bahan terhadap medan
magnet (dZ/dB) sebagai fungsi medan magnet (B), seperti Gambar 4.25 berikut.

Gambar 4.25 Spektrum resonansi siklotron Azbel-Kaner
untuk bahan tembaga pada suhu T=4,2 K
Absorbsi maksimum pada elektron dengan orbit terbesar terjadi pada permukaan
Fermi yang penampang lintangnya tegak lurus B. Oleh karena itu dengan mengubah
orientansi B, dapatlah diukur orbit elektron dalam berbagai arah, sehingga
rekonstruksi permukaan Fermi dapat dibuat. Percobaan ini, umumnya, dilakukan
pada suhu yang sangat rendah (sekitar 4 K) pada sampel yang murni dan berbentuk
kristal tunggal, dan pada medan magnet yang sangat besar (sekitar 100 kG). Kondisi



ini menyebabkan waktu tumbukan τ cukup panjang, dan frekuensi siklotron ωc cukup
tinggi (daerah gelombang mikro), sehingga ωcτ>>1 terpenuhi dan “skin depth” cukup
dalam.
RINGKASAN
01. Apabila deretan ion tersusun teratur dan membentuk kisi kristal, maka energi
potensial kristalnya berubah secara periodik sesuai dengan periodisitas kisi
tersebut. Teori pita energi zat padat mengajukan model tentang elektron dalam
kristal dengan asumsi sebagai berikut. (a). Terdapat energi potensial V (r ) yang
tidak sama dengan nol di dalam kristal dengan keberkalaan kisi kristal, (b). Fungsi
gelombang ψ (r ) dibuat berdasarkan kisi sempurna dan dimana dianggap bahwa
kisi tidak bervibrasi secara termal, (c). Teori pita energi dikembangkan dari
bahasan perilaku elektron tunggal di bawah pengaruh suatu potensial periodik
V (r ) yang merepresentasikan semua interaksi, baik dengan ion kristal maupun
dengan sesama elektron lain, (d). Bahasan elektron tunggal dapat menggunakan
persamaan Schrodinger untuk satu elektron, dan dengan ketentuan bahwa
pengisian keadaan elektron yang diperoleh menganut distribusi Fermi-Dirac.
02. Elektron dalam potensial periodik logam memenuhi teorema Bloch, yaitu
“Fungsi eigen (fungsi Bloch) dari persamaan gelombang untuk suatu potensial
periodik adalah hasilkali antara suatu gelombang bidang berjalan eksp (ik • r ) dan
suatu fungsi modulasi u k (r ) dengan periodisitas kisi kristal”.

03. Untuk menyelesaikan perilaku elektron Bloch digunakanlah Model Kronig-
Penney, yang menelaah gerak elektron dalam suatu potensial persegi periodik,
sebagai penyederhanaan bentuk potensial sebenarnya. Hasil model ini adalah

sin (α a ) + cos(α a ) = cos ka . Ungkapan energi elektron, yang tersirat dalam α,
P
αa
memiliki karakter (a). Spektrum energi elektron terdiri dari beberapa pita energi
(daerah energi) yang diperkenankan dan beberapa yang terlarang, (b). Lebar pita
energi yang diperkenankan bertambah lebar dengan meningkatnya energi



elektron, (c). Lebar pita energi tertentu yang diperkenankan mengecil apabila
“energi ikatan” makin naik, (d). Celah energi terjadi pada harga k= nπ/a, dengan n
= ±1, ±2, ±3, …
04. Pada titik k= nπ/a terjadi gelombang tegak dan memenuhi kondisi refleksi Bragg.
Pada titik ini, elektron dapat direpresentasikan sebagai fungsi gelombang yang
selama sebagian besar dari waktunya berada (a) di dekat inti atom (x=ma), atau
(b) dalam ruang di antara inti atom (jauh dari inti atom). Energi di kidua tempat
ini berbeda dan beda energi elektron antara keduanya pada batas k==±π/a ini
merupakan celah energi.
05. Ada dua hal, dimana medan listrik luar tidak menghasilkan arus elektron dalam
kristal, yaitu (a). pita energi yang diperkenankan sama sekali tidak dihuni
elektron, dan (b). pita energi yang diperkenankan terisi penuh oleh elektron, atau
semua keadaan elektron terisi penuh oleh elektron. Berarti, hanya pita energi yang
terisi sebagian (atau yang kosong sebagian) dapat memberikan sumbangan pada
arus listrik. Hal ini menghasilkan dua jenis pembawa muatan, yaitu elektron
(negatip) dan hole (positip).
06. Ciri isolator adalah semua energi terisi penuh oleh elektron atau sama sekali
kosong, sehingga tidak dapat terjadi konduksi listrik. Celah energi ΔE cukup
besar, sehingga elektron dari pita energi yang penuh tidak dapat melompat (karena
energi termal) ke pita energi yang kosong. Tingkat energi Fermi EF melalui daerah
energi yang kosong. Ciri konduktor adalah tingkat energi Fermi EF melewati pita
energi yang diperkenankan, sehingga pita tersebut setengahnya (atau sebagiannya)
terisi oleh elektron. Ciri semikonduktor adalah tingkat energi Fermi EF melewati
daerah harga energi terlarang, sehingga pada T=0 K hanya ada pita yang sama
sekali penuh, dan di atasnya pita energi yang kosong sama sekali. Celah energi ΔE
tidak tinggi, sehingga pada T>0 K sebagian elektron dapat melompatinya, dan
berpindah ke pita konduksi yang masih kosong. Sementara tempat yang
ditinggalkan elektron menjadi hole dalam pita valensi. Dengan demikian,
pembawa muatannya adalah elektron dan hole. Sedangkan ciri semilogam adalah



celah energi lenyap seluruhnya, atau bahkan kedua pita energi terjadi overlap
tipis.
07. Metode LCAO menganggap bahwa elektron terikat kuat pada atom. Fungsi
gelombang elektron didasarkan pada fungsi gelombang elektron dalam atom
yang terisolasi, dan disusun dari fungsi gelombang elektron termaksud. Hasil

∑e
ik •( rn − r j )
metode ini adalah ungkapan energi elektron E = E o − α − β . Untuk
j

kisi kubik sederhana dengan rusuk a, ungkapan energinya E(k)=Eo-α-2β(cos kxa+
cos kya+cos kza). Hal ini berarti (a). E(k) periodik terhadap k, (b). E(k) = E(-k),
(c). E(k)max=Eo-α+6β pada puncak pita, dan E(k)min=Eo-α-6β pada dasar pita,
sehingga beda antara keduanya merupakan pita energi, yang besarnya sebanding
dengan integral overlap. Rentang energi dalam pita energi ini berperan sebagai
energi kinetik elektron, sehingga elektron mampu bergerak ke bagian seluruh

kristal, (d). Untuk harga k sangat kecil, yakni di dekat dasar pita energi elektron

menjadi E(k) ≅ Eo - α - 6β + β a2 k2. Terlihat bahwa harga energi ini sama dengan
hubungan dispersi untuk elektron bebas.
08. Kecepatan dan massa efektif elektron, masing-masing dinyatakan sebagai
1 1 1
vg = ∇ k E (k ) dan = 2 ∇ k (∇ k E ) . Misalnya untuk kisi kubik sederhana
m*
dan elektron bebas dapat dicari ungkapan keduanya.
09. Pengaruh gaya luar F terhadap elektron adalah adanya perubahan momentum.
Karena bentuk E(k) dan kecepatan elektron yang sebanding dengan gradien
energi, maka gerak elektron hanya bolak-balik antara x=0 sampi x=xo. Setiap kali
elektron berada di x=xo, energinya berada di puncak pita konduksi dimana
kemudian terjadi refleksi Bragg.
10. Teori pita energi menghasilkan ungkapan umum konduktivitas listrik
σ = e 2 v F , xτ F g ( E F ) . Bila didekati dengan permukaan Fermi sferik, maka
2

didapatkan ungkapan konduktivitas yang hanya berlaku untuk model elektron
bebas.



11. Teori pita energi menghasilkan ungkapan umum konstanta Hall
Reσ e2 + Rhσ h
2
R= . Jika pembawa muatan hanya elektron, maka Rh dan σh
(σ e + σ h )2
berharga nol, sehingga R=Re. Hal ini didapat pada model elektron bebas.
12. Teori pita energi menghasilkan ungkapan umum frekuensi siklotron untuk
2π eB
elektron Bloch ini adalah ωc = . Bila didekati dengan bentuk
δk
∫ v(k )
E=( 2k2/2m*), maka ungkapan frekuensi yang sama dengan yang diperoleh oleh

model elektron bebas.

LATIHAN SOAL BAB IV
01.a. Fungsi Bloch satu dimensi mempunyai bentuk ψk(x)=eikxuk(x). Jika fungsi
tersebut dikenai syarat batas periodik, maka buktikanlah bahwa jumlah
(keadaan) orbital dalam suatu pita energi dalam Zona Brillouin Pertama sama
dengan jumlah sel satuan primitip dalam kristal!
b. Sama dengan soal a), tetapi untuk soal SC dalam tiga dimensi!
02.a. Diketahui bahwa kristal BCC memiliki 8 tetangga terdekat dengan posisi
1
2
(
ˆ ˆ ˆ
a x+ y−k ) 1
2
(ˆ ˆ ˆ
a −x+ y−k ) 1
2
(
ˆ ˆ ˆ
a x− y−k ) 1
2
(ˆ ˆ ˆ
a −x− y−k )
1
2 a (x − y + k )
ˆ ˆ ˆ 1
2 a (− x − y + k )
ˆ ˆ ˆ 1
2 a (x + y + k )
ˆ ˆ ˆ 1
2 a (− x + y + k )
ˆ ˆ ˆ

(1) Dengan menggunakan ungkapan energi elektron (4.38) dan pendekatan
interaksi tetangga terdekat, buktikan bahwa ungkapan energi untuk kristal
BCC adalah
E(k) = Eo - α - 8β cos ½ kxa cos ½ kya cos ½ kza
(2) Tentukan lebar pita energinya!
(3) Gambarkan kontur energi tersebut dalam bidang kx-ky!



b. Sama dengan soal a), tetapi untuk kristal FCC! Diketahui bahwa kristal FCC
memiliki 12 tetangga terdekat dengan posisi
1
2
(ˆ ˆ
a y−k ) 1
2
( ˆ ˆ
a − y−k ) 1
2
( ˆ ˆ
a− y+k ) 1
2
(ˆ ˆ
a y+k )
1
2 a(x + y )
ˆ ˆ 1
2 a(x − y )
ˆ ˆ 1
2 a(− x − y )
ˆ ˆ 1
2 a(− x + y )
ˆ ˆ
1
2
(ˆ ˆ
a x−k ) 1
2
(ˆ ˆ
a x+k ) 1
2
( ˆ ˆ
a −x+k ) 1
2
( ˆ ˆ
a −x−k )
Buktikan bahwa ungkapan energi untuk kristal FCC adalah
E(k) = Eo - α - 4β [cos ½ kya cos ½ kza + cos ½ kza cos ½ kxa
+ cos ½ kxa cos ½ kya]
03.a. Dengan menggunakan model ikatan kuat, hitunglah massa efektif elektron
dalam kisi dimensi satu! Gambarkan massa m* terhadap k, dan tunjukkan
bahwa massa tersebut tidak bergantung pada k hanya di dekat pusat dan di
dekat ujung zona!
b. Hitunglah massa efektif pada pusat zona dalam suatu kisi SC!
c. Sama dengan soal b), tetapi pada ujung zona sepanjang arah [111]!
04. Dengan menggunakan model ikatan kuat, hitunglah massa efektif elektron pada
kristal SC! Isotropkah massa tersebut?
05.a. Hitunglah kecepatan elektron untuk kristal satu dimensi dalam model ikatan
kuat dan buktikan bahwa kecepatan tersebut nol pada batas zona!
b. Sama dengan soal a), tetapi untuk kisi bujursangkar! Tunjukkan bahwa
kecepatan pada batas zona adalah paralel terhadap batas tersebut! Jelaskan hasil
ini dengan menggunakan refleksi Bragg!
c. Sama dengan soal a), tetapi untuk kisi SC tiga dimensi, dan tunjukkan bahwa
kecepatan elektron pada permukaan zona adalah paralel terhadap permukaan
tersebut! Jelaskan hal ini dengan menggunakan refleksi Bragg! Kemukakan
pernyataan umum tentang arah kecepatan pada permukaan zona tersebut!
06. Semikonduktor Si dan Ge mempunyai relasi dispersi berkontur ellips
E (k ) = α 1 k x2 + α 2 k y + α 3 k z2
2

a. Buktikanlah bahwa bahan tersebut mempunyai massa elektron anisotrop!



b. Apa yang akan terjadi jika αi dalam ungkapan relasi dispersi di atas berharga
negatip?
07. Elektron Bloch berosilasi periodik dalam pengaruh medan listrik.
a. Tuliskan ungkapan perioda gerakan dalam “reduced-zone scheme”!
b. Jika perioda tersebut berorde 10-5 s dan waktu tumbukan elektron berorde 10-14s,
maka hitunglah jumlah tumbukan yang dialami elektron selama satu putaran
geraknya! Apakah konsekuensi dari jumlah tumbukan tersebut?
08. Medan listrik statik dikenakan pada sebuah elektron pada waktu t=0 saat elektron
berada di dasar pita energi.
a. Tunjukkan bahwa dalam satu dimensi posisi elektron dalam ruang sebenarnya
1 ⎛ F ⎞
pada saat t adalah X = X o + E ⎜ k = t ⎟ , dengan Xo adalah posisi awal dan
F ⎝ ⎠
F=-eε adalah gaya listrik!
b. Apakah gerakan dalam soal a) periodik? Jelaskan!
09.a. Tentukan harga k yang mana kecepatan elektron mencapai maksimum pada kisi
kristal satu dimensi!
b. Bagaimana ungkapan m* pada harga k soal a)?
10. Turunkan ungkapan konstanta Hall (4.63) untuk sistem elektron-hole!
2 2
11. Suatu kristal mempunyai kontur energi E (k ) = *
k +
2
x *
2
k y . Jika medan
2m 1 2m 2

magnet tegak lurus terhadap bidang kontur, maka buktikan bahwa frkuensi

e2
siklotron adalah ω C = * *
B !
m1 m2


BAB V
SEMIKONDUKTOR

Semikonduktor, umumnya, diklasifikasikan berdasarkan harga resistivitas
listriknya pada suhu kamar, yakni dalam rentang (10-2 sampai 109) Ωm. Resistivitas
yang lebih tinggi dimiliki oleh bahan isolator, dan yang lebih rendah oleh bahan
konduktor. Resistivitas listrik dipengaruhi oleh suhu, cahaya yang menyinari, medan
listrik dan medan magnet.
Semikonduktor sangat luas pemakaiannya, terutama, sejak ditemukannya
transistor pada akhir tahun 1940-an. Oleh karena itu semikonduktor dipelajari secara
intensif dalam fisika zat padat. Namun, dalam bab ini, hanya dibahas sifat fisis dasar
semikonduktor saja.
Permulaan bab ini menyajikan pengelompokan semikonduktor berdasarkan
unsur pembentuknya, beserta jenis struktur kristal dan ikatannya. Berdasarkan murni
atau tidak murninya bahan, semikonduktor dibedakan menjadi dua jenis, yaitu
semikonduktor intrinsik dan ekstrinsik.
Semikonduktor intrinsik adalah semikonduktor murni, yang sifat
kelistrikannya ditentukan oleh sifat alam yang melekat pada unsur yang
bersangkutan. Sedangkan semikonduktor ekstrinsik adalah semikonduktor tidak
murni, yang sifat kelistrikannya dikendalikan oleh sifat dan jumlah pengotor yang
diberikan pada bahan itu.
Dalam menyajikan sifat fisis dasar semikonduktor, bab ini membahas rapat
elektron dan hole, yakni partikel pembawa muatan dalam semikonduktor. Umumnya,
jarang ditemukan semikonduktor murni, melainkan dalam keadaan dengan

5 SEMIKONDUKTOR 140

ketidakmurnian. Bab ini juga membahas pengaruh ketakmurnian pada rapat elektron
dan hole. Disamping itu, juga dibahas konduktivitas listrik dalam semikonduktor.
Akhirnya, bab ini ditutup oleh bahasan metode optik yang dapat digunakan untuk
mengukur celah energi.

5.1 KLASIFIKASI SEMIKONDUKTOR

Dilihat dari unsur pembentuknya, semikonduktor diklasifikasikan menjadi
beberapa kelompok berikut.
a. Semikonduktor elemental kelompok IV, misalnya Ge dan Si. Kelompok ini
memiliki struktur kristal intan dan ikatan kovalen homopolar.
b. Senyawa kelompok III-V, misalnya GaAs, GaP, InSb, InAs dan GaSb. Senyawa ini
memiliki struktur seng sulfida. Ikatannya berbentuk kovalen heteropolar, karena
distribusi elektron sepanjang ikatan lebih banyak menuju ke arah atom yang
elektronegativitasnya lebih tinggi, sehingga tidak simetri. Karena sifat polar inilah
kisi senyawa III-V dapat dipolarisasikan oleh pemakaian medan listrik.
c. Senyawa kelompok II-VI, misalnya CdS dan ZnS yang berstruktur seng sulfida dan
berikatan kovalen heteropolar.
d. Senyawa kelompok IV-VI, misalnya PbTe.

5.2 SEMIKONDUKTOR INTRINSIK

Pada T=0 K, pita valensi semikonduktor terisi penuh elektron, sedangkan pita
konduksi kosong. Kedua pita tersebut dipisahkan oleh celah energi kecil, yakni dalam
rentang (0,18 – 3,7) eV. Pada suhu kamar, Si dan Ge masing-masing memiliki celah
energi 1,11 eV dan 0,66 eV. Pita konduksi dan pita valensi semikonduktor, masing-
masing sebagai pita antibonding dan bonding dari keadaan elektron valensi atom
yang bersangkutan.
Bila mendapat cukup energi, elektron dapat melepaskan diri dari ikatan
kovalen dan tereksitasi menyeberangi celah energi. Elektron ini bebas bergerak di
antara atom. Sedangkan tempat kekosongan elektron disebut hole, segera terisi
elektron ikatan kovalen lainnya. Holepun berpindah, begitu seterusnya. Dengan


5 SEMIKONDUKTOR 141

demikian dasar pita konduksi dihuni oleh elektron, dan puncak pita valensi dihuni
hole. Sekarang, kedua pita terisi sebagian, dan dapat menimbulkan arus netto bila
dikenakan medan listrik.
Elektron dan hole, masing-masing sebagai pembawa muatan bebas negatip
dan positip dalam semikonduktor, mengikuti distribusi Fermi-Dirac. Dalam
semikonduktor murni, elektron dan hole mempunyai konsentrasi sama.
Semikonduktor yang demikian disebut semikonduktor intrinsik.
Distribusi elektron dalam pita konduksi mengikuti distribusi Fermi-Dirac
sama seperti persamaan (3.27), yaitu
1
f e (E) = E − EF
(5.1a)
1+ e kT

Dengan mengandaikan bahwa (E-EF)>>kT, maka distribusi (5.1a) di atas menjadi
EF − E

f e (E) ≅ e kT
(5.1b)

Tampak bahwa probabilitas orbital elektron konduksi untuk terisi elektron sangat
kecil fe(E)<<1. Energi elektron dalam pita konduksi adalah
2
k2
E (k ) = E c + (5.2)
2me
dengan Ec = tingkat energi dasar pita konduksi
me = massa efektif elektron
Oleh karena itu rapat keadaan elektron, dengan mengacu pada persamaan (3.26),
adalah
3/ 2
1 ⎛ 2me ⎞
g e (E) = ⎜ ⎟ (E − Ec )1 / 2 (5.3)
2π 2 ⎝ 2 ⎠
dengan tingkat energi referensi diambil pada dasar pita konduksi Ec. Dengan
mengggunakan (5.1b) dan (5.3) diperoleh rapat elektron di pita konduksi
∞ 3/ 2 ∞ EF − E
1 ⎛ 2me ⎞
∫ ∫ (E − E c ) e
1/ 2
ne = f e ( E ) g e ( E ) dE = ⎜ ⎟ kT
dE (5.4)
Ec 2π 2 ⎝ 2 ⎠ Ec

Dengan mengubah variabel, dan menggunakan bentuk


5 SEMIKONDUKTOR 142

∞
π
∫x e − x dx =
1/ 2

0
2

maka konsentrasi elektron (5.4) dapat direduksi menjadi
3/ 2 Ec − E F
⎛ 2π me kT ⎞ −
ne = 2⎜ 2
⎟ e kT
(5.5)
⎝ h ⎠
3/ 2
⎛ 2π me kT ⎞
Faktor 2⎜ 2
⎟ menyatakan rapat keadaan efektif dalam pita konduksi.
⎝ h ⎠
Dalam hubungan (5.5) di atas, energi Fermi EF belum diketahui.
Distribusi hole dalam pita valensi dapat dituliskan
E − EF
1
f h (E) = 1 − f e (E) = EF − E
≅e kT
(5.6)
1+ e kT

apabila dianggap bahwa (EF-E)>>kT. Energi hole dalam pita valensi
2
k2
E (k ) = E v + (5.7)
2mh
dengan Ev = tingkat energi puncak pita valensi
mh = massa efektif hole
Oleh karena itu rapat keadaan hole
3/ 2

g h (E) =
1 ⎛ 2m h ⎞
⎜ ⎟ (E −E )1/ 2
(5.8)
2π 2 ⎝ 2 ⎠
v

dengan mengambil tingkat referensi puncak pita valensi Ev. Dengan menggunakan
(5.6) dan (5.8) diperoleh rapat hole di pita valensi
Ev

nh = ∫f
−∞
h ( E ) g h ( E ) dE

3 / 2 Ev E − EF

∫ (E )
1 ⎛ 2m h ⎞ 1/ 2
= ⎜ ⎟ −E e kT
dE (5.9)
2π 2 ⎝ 2 ⎠
v
−∞
3/ 2 E F − Ev
⎛ 2π mh kT ⎞ −
= 2⎜ 2
⎟ e kT

⎝ h ⎠


5 SEMIKONDUKTOR 143

3/ 2
⎛ 2π m h kT ⎞
Faktor 2⎜ ⎟ menyatakan rapat keadaan efektif dalam pita valensi. Energi
⎜ ⎟
⎝ h2 ⎠
Fermi EF dalam hubungan inipun belum diketahui.
Sebenarnya, dalam menurunkan ungkapan rapat elektron dan hole di atas
tidak dinyatakan bahwa bahan tersebut semikonduktor intrinsik atau ekstrinsik.
Dengan demikian ungkapan di atas berlaku agak umum.
Bila rapat elektron (5.5) dikalikan dengan rapat hole (5.9) diperoleh
3
⎛ 2π kT ⎞
Eg
3/ 2 −
ne nh = 4⎜ 2 ⎟ (me mh ) e kT (5.10)
⎝ h ⎠
karena celah energi Eg=Ec-Ev. Hubungan ini disebut hukum Aksi-Massa.
Ungkapannya tidak bergantung pada EF, dan jenis bahan murni atau didoping. Pada
suhu tertentu T, perkalian nenh berharga konstan dan rapat pembawa muatan yang
satu dapat dihitung bila rapat pembawa muatan lainnya diketahui.
Semikonduktor intrinsik harus memenuhi hubungan
ne = nh (5.11)
Substitusi ne dari (5.5) dan nh dari (5.9) ke dalam (5.11) menghasilkan ungkapan
energi Fermi EF relatif terhadap energi puncak pita valensi Ev
Eg 3 m
Ec − E F = + kT ln e (5.12)
2 4 mh
Karena kT<<Eg, maka suku kedua dapat diabaikan, sehingga EF tepat di tengah-
tengah antara Ev dan Ec. Karena persamaan (5.11), maka dari persamaan (5.10) dapat
diperoleh rapat elektron atau hole dalam semikonduktor intrinsik
3/ 2
⎛ 2π kT ⎞
Eg
−
ne = nh = 2⎜ 2 ⎟ (me mh )3 / 4 e 2 kT
(5.13)
⎝ h ⎠
Tampak bahwa n naik secara tajam (secara eksponensial) terhadap suhu T. Pada
Gambar 5.1 berikut disajikan sketsa pita konduksi dan valensi, fungsi distribusi dan
rapat keadaan elektron dan hole.


5 SEMIKONDUKTOR 144

Gambar 5.1 a. Pita valensi dan konduksi
b. Fungsi distribusi
c. Rapat keadaan elektron dan hole
Ungkapan konsentrasi (5.13) di atas dapat dipergunakan untuk menetapkan Eg
bagi bahan semikonduktor intrinsik. Jika μe dan μh, masing-masing menyatakan
mobilitas elektron dan hole, maka dengan menggunakan (5.13) diperoleh
konduktivitas total
σ = e ne μ e + e n h μ h
3/ 2
⎛ 2π kT ⎞
Eg
−
= 2e⎜ 2 ⎟ (me mh )
3/ 4
e 2 kT
(μ e + μ h ) (5.14)
⎝ h ⎠
Eg
−
= f (T ) e 2 kT

dengan f(T) adalah fungsi yang bergantung lemah terhadap suhu. Dengan membuat
grafik ln σ sebagai fungsi 1/T, dari data eksperimen, maka didapatkan kemiringan
kurva –Eg/2k. Dengan demikian celah energi Eg dapat ditentukan. Pada awal
perkembangan semikonduktor, cara ini merupakan prosedur standard dalam
menentukan celah energi Eg.

5.3 SEMIKONDUKTOR EKSTRINSIK

Ketidakmurnian dalam semikonduktor dapat menyumbangkan elektron
maupun hole dalam pita energi. Dengan demikian, konsentrasi elektron dapat menjadi


5 SEMIKONDUKTOR 145

tidak sama dengan konsentrasi hole, namun masing-masing bergantung pada
konsentrasi dan jenis bahan ketidakmurnian. Semikonduktor yang didoping dengan
ketidakmurnian disebut semikonduktor ekstrinsik.

5.3.1 Ketidakmurnian Donor dan Aseptor
Dalam aplikasi, kadang hanya diperlukan bahan dengan pembawa muatan
elektron saja, atau hole saja. Hal ini dilakukan dengan doping ketidakmurnian ke
dalam semikonduktor.

5.3.1.1 Donor
Misalnya, Si didoping dengan As. Atom As menempati titik kisi yang
sebelumnya ditempati tuan rumah Si secara acak. As adalah pentavalen, sedangkan
Si tetravalen. Kelebihan sebuah elektron dari setiap atom As, yang tidak turut dalam
ikatan tetrahedral Si, bebas bergerak dalam kristal sebagai elektron konduksi dalam
pita konduksi. Oleh karena itu, ketidakmurnian menjadi ion positip As+. Hal ini
berarti ketidakmurnian As menyumbangkan elektron ke dalam pita konduksi, dan
disebut donor.
Orbit elektron bebas di sekitar donor tersebut ternyata menyerupai atom
hidrogen model Bohr. Dengan demikian, interaksi yang terjadi adalah interaksi
Coulomb. Dengan memakai model Bohr, maka jari-jari elektron donor
⎛m ⎞
rd = ε r ⎜ o
⎜m ⎟ao
⎟ (5.15)
⎝ e ⎠
dengan εr = konstanta dielektrik kristal
ao = radius Bohr (=0,53 Å)
mo= massa bebas elektron
me= massa efektif elektron
Si memiliki konstanta dielektrik εr=11,7 dan (me/mo)=0,2. Oleh karena itu, harga rd
untuk Si kira-kira 60 kali lebih besar daripada ao. Karena itu orbit elektron donor
melingkupi banyak atom “tuan rumah” Si, seperti ditunjukkan oleh Gambar 5.2
berikut.


5 SEMIKONDUKTOR 146

Gambar 5.2 Orbit elektron mengelilingi donor
Sedangkan energi ikat yang bersesuaian dengan keadaan dasar energi

1 ⎛ me ⎞
Ed = + ⎜ ⎟ Eo (5.16)
ε r 2 ⎜ mo
⎝
⎟
⎠

dengan Eo adalah energi dasar atom hidrogen (-13,6 eV). Hal ini berarti, untuk Si,
harga Ed kira-kira 700 kali lebih kecil daripada Eo. Dengan demikian, tingkatan
energi donor dalam semikonduktor berada dalam celah energi sedikit di bawah dasar
pita konduksi, seperti ditunjukkan oleh Gambar 5.3 berikut.

Gambar 5.3 Tingkat energi donor Ed dalam semikonduktor

Pada suhu kamar (kT=0,025 eV), sebagian besar donor terionisasi dan elektronnya
tereksitasi ke dalam pita konduksi. Jika semua donor terionisasi, maka konsentrasi
elektron dalam pita konduksi hampir sama dengan jumlah donor.


5 SEMIKONDUKTOR 147

5.3.1.2 Aseptor

Misalnya, kristal Si didoping dengan atom Ga. Karena atom Ga trivalen, maka
pada salah satu ikatan elektronnya terjadi hole. Hole segera terisi oleh elektron dari
ikatan yang lain sehingga terjadi hole pada ikatan yang lain tadi. Pada akhirnya, hole
tersebut secara bebas bergerak ke seluruh bagian kristal. Karena cenderung menerima
elektron untuk melengkapi ikatan tetrahedralnya, ketidakmurnian Ga menjadi ion
negatip dan disebut aseptor.

Orbit hole di sekitar aseptor juga menyerupai atom hidrogen model Bohr.
Energi ikat hole pada aseptor juga sangat kecil harga numeriknya, dan terletak dalam
celah energi, sedikit di atas pita valensi, seperti ditunjukkan dalam Gambar 5.4
berikut.

Gambar 5.4 Tingkat energi aseptor Ea dalam semikonduktor

Saat aseptor terionisasi (karena hole terisi elektron yang tereksitasi dari puncak pita
valensi), hole jatuh ke puncak pita valensi, dan menjadi pembawa muatan bebas.

Tingkat energi donor dan aseptor dalam celah energi (pita energi terlarang)
merupakan konsekuensi dari ketidaksempurnaan kristal. Kedua tingkatan ini
terlokalisasi dan tidak bisa menghantarkan listrik.


5 SEMIKONDUKTOR 148

Umumnya, tidak ada semikonduktor yang benar-benar murni, melainkan
mengandung donor maupun aseptor. Elektron dalam pita konduksi dapat tercipta
melalui eksitasi antarpita atau ionisasi termal donor. Hole dalam pita valensi dapat
terbentuk melalui eksitasi antarpita atau eksitasi termal elektron dari pita valensi ke
dalam tingkatan aseptor. Dapat juga, elektron jatuh dari tingkat donor ke tingkat
aseptor.

Semikonduktor intrinsik diperoleh bila doping ketidakmurnian kecil. Dengan
demikian, konsentrasi pembawa muatan sangat ditentukan oleh transisi antarpita
secara induksi termal, sehingga diperoleh pendekatan ne=nh (persamaan (5.11)) dan
konsentrasi elektron atau hole sama seperti persamaan (5.13), yaitu
3/ 2
⎛ 2π kT ⎞
Eg
−
ne = nh = ni = 2⎜ 2 ⎟ (me mh )3/ 4
e 2 kT
(5.17)
⎝ h ⎠

Pada suhu yang cukup tinggi, semua semikonduktor berada dalam keadaan intrinsik,
yaitu ni naik secata tajam (secara eksponensial) terhadap suhu T (kecuali konsentrasi
ketidakmurnian tinggi sekali).

Semikonduktor ekstrinsik diperoleh bila doping ketidakmurnian cukup besar,
sehingga konsentrasi intrinsik sudah jauh lebih kecil pada suhu kamar. Daerah
ekstrinsik terbagi menjadi dua kelompok berikut.

a. Konsentrasi donor Nd jauh lebih besar daripada aseptor Na

Dianggap semua donor terionisasi, sehingga diperoleh pendekatan

ne = Nd (5.18)

Bila hukum Aksi-Massa dikaitkan dengan konsentrasi intrinsik, maka diperoleh

ne nh = ni2 (5.19)

Substitusi konsentrasi donor (5.18) ke dalam (5.19) menghasilkan konsentrasi hole

ni2
nh = (5.20)
Nd


5 SEMIKONDUKTOR 149

Di daerah ekstrinsik berlaku ni<<Nd, sehingga nh<<Nd. Dengan demikian, konsentrasi
elektron (dari donor) jauh lebih besar daripada hole. Semikonduktor yang demikian
disebut semikonduktor jenis-n.

b. Konsentrasi aseptor Na jauh lebih besar daripada donor Nd

Analisa yang sama dengan di atas memberikan pendekatan

nh = Na (5.21)

Konsentrasi elektron kecil, yang diungkapkan oleh

ni2
ne = (5.22)
Na

Semikonduktor yang demikian disebut semikonduktor jenis-p.

5.4 PENGUKURAN CELAH ENERGI DENGAN METODE OPTIK

Nilai terendah kurva dispersi pita konduksi semikonduktor, ternyata, tidak
hanya satu nilai pada k=0, melainkan bisa juga terjadi beberapa nilai pada k≠0. hal ini
ditunjukkan oleh sketsa dalam Gambar 5.5 berikut.

pita
konsuksi

Eg Eg

pita pita
valensi valensi

a b

Gambar 5.5 a. Semikonduktor celah-langsung
b. Semikonduktor celah-tidak langsung
Pada semikonduktor celah-langsung, misalnya GaAs dan InSb, elektron
mengabsorbsi foton dan langsung melompat ke dalam pita konduksi. Energi foton
harus sama atau lebih besar dari celah energi. Koefisien absorbsi α=α(λ) mencapai


5 SEMIKONDUKTOR 150

harga maksimum pada panjang gelombang ambang foton λ0. Dengan demikian celah
energi dapat ditentukan melalui hubungan

hc
Eg = (5.23)
λ0

Pada semikonduktor celah-tidak langsung, misalnya Si dan Ge, elektron
mengabsorbsi foton dan fonon sekaligus. Proses ini memenuhi hukum kekekalan
energi

Efoton + Efonon = Eg (5.24)

Karena Efonon(=0,05 eV) sangat kecil bila dibandingkan dengan Efoton(=1 eV), maka

hc
E g = E foton = (5.25)
λ0

sehingga dalam hal ini sama dengan kasus transisi langsung pada semikonduktor
celah-langsung.

RINGKASAN
01. Dilihat dari unsur pembentuknya, semikonduktor diklasifikasikan menjadi
beberapa kelompok berikut: (a). elemental kelompok IV, yang berstruktur kristal
intan dan ikatan kovalen homopolar, (b). kelompok III-V, yang berstruktur seng
sulfida dan ikatannya berbentuk kovalen heteropolar, (c). kelompok II-VI, yang
berstruktur seng sulfida dan berikatan kovalen heteropolar, dan (d). kelompok IV-
VI.
02. Pada T=0 K, pita valensi semikonduktor terisi penuh elektron, sedangkan pita
konduksi kosong. Kedua pita tersebut dipisahkan oleh celah energi kecil, yakni
dalam rentang (0,18 – 3,7) eV. Dasar pita konduksi dihuni oleh elektron, dan
puncak pita valensi dihuni hole. Sekarang, kedua pita terisi sebagian, dan dapat
menimbulkan arus netto bila dikenakan medan listrik. Keduanya mengikuti
distribusi Fermi-Dirac. Dalam semikonduktor murni, elektron dan hole


5 SEMIKONDUKTOR 151

mempunyai konsentrasi sama. Semikonduktor yang demikian disebut
semikonduktor intrinsik.
3/ 2 Ec − E F
⎛ 2π me kT ⎞ −
03. Konsentrasi elektron dalam pita valensi adalah ne = 2⎜ 2
⎟ e kT
.
⎝ h ⎠
3/ 2 E F − Ev
⎛ 2π mh kT ⎞ −
Sedangkan hole di pita valensi adalah n h = 2⎜ 2
⎟ e kT
. Hukum Aksi-
⎝ h ⎠
Massa adalah perkalian antara rapat elektron dengan rapat hole
04. Letak tingkat energi Fermi EF relatif terhadap energi puncak pita valensi Ev untuk
semikonduktor intrinsik adalah tepat di tengah-tengah antara Ev dan Ec.
Eg
−
05. Konduktivitas sebagai fungsi suhu dinyatakan oleh σ = f (T ) e 2 kT
. Dengan
membuat grafik ln σ sebagai fungsi 1/T, dari data eksperimen, maka didapatkan
kemiringan kurva –Eg/2k. Dengan demikian celah energi Eg dapat ditentukan.
06. Semikonduktor yang didoping dengan ketidakmurnian disebut semikonduktor
ekstrinsik. Semikonduktor yang tetravalen, didoping dengan atom pentavalen.
Akibatnya, kelebihan sebuah elektron dari setiap atom donor, bebas bergerak
dalam kristal sebagai elektron konduksi dalam pita konduksi. Tetapi, jika
didoping dengan atom trivalen, maka pada salah satu ikatan elektronnya terjadi
hole sehingga atom pendoping tersebut menjadi aseptor.
07. Orbit elektron bebas di sekitar donor dan hole di sekitar aseptor tersebut, ternyata,
menyerupai atom hidrogen model Bohr. Dengan demikian, interaksi yang terjadi
adalah interaksi Coulomb. Jari-jarinya kira-kira 60 kali lebih besar daripada radius
Bohr sehingga melingkupi banyak atom “tuan rumah”. Tingkat energi donor
dalam semikonduktor berada dalam celah energi sedikit di bawah dasar pita
konduksi. Sedangkan energi ikat hole pada terletak dalam celah energi, sedikit di
atas pita valensi.
08. Dalam semikonduktor ekstrinsik, jika konsentrasi donor Nd jauh lebih besar
daripada aseptor Na, konsentrasi elektron (dari donor) jauh lebih besar daripada
hole. Semikonduktor yang demikian disebut semikonduktor jenis-n. Tetapi
sebaliknya, jika konsentrasi aseptor Na jauh lebih besar daripada donor Nd, maka


5 SEMIKONDUKTOR 152

konsentrasi elektron kecil. Semikonduktor yang demikian disebut semikonduktor
jenis-p.

09. Pengukuran celah energi dengan menggunakan metode optik memenuhi rumus
hc
hubungan E g =
λ0

LATIHAN SOAL BAB V
01. Model sederhana menunjukkan bahwa Ge memiliki pita valensi dan pita konduksi
tunggal dengan celah energi 0,670 eV. Sedangkan massa efektifnya mh=0,370mo
dan me=0,550mo. Hitunglah
a. energi Fermi relatif terhadap puncak pita valensi!
b. probabilitas terisinya keadaan dasar pita konduksi pada suhu 300 K!
c. probabilitas kosongnya keadaan puncak pita valensi pada suhu 300 K!
d. konsentrasi elektron dalam pita konduksi pada suhu 300 K!
02. Suatu bahan semikonduktor mempunyai struktur intan dengan sisi kubus 5,4 Å,
massa efektif me=0,88mo dan mh=0,42mo serta celah energi antara pita valensi
dan konduksi sebesar 0,82 eV. Diandaikan bahan tersebut murni, maka hitunglah
a. energi Fermi!
b. rapat elektron dalam pita konduksi pada suhu 300 K!
c. rapat elektron dalam pita valensi pada suhu 300 K!
d. Buktikan bahwa rapat elektron dalam pita konduksi sama dengan rapat hole
dalam pita valensi pada suhu 300 K!
03.a. Hitunglah konsentrasi elektron dan hole dalam sampel murni Si pada suhu
kamar! Ambillah harga me=0,7mo; mh=mo dan Eg=1,1 eV!
b. Tentukan posisi tingkat energi Fermi dalam keadaan ini!
04. Diketahui bahwa rapat keadaan efektif elektron dalam pita konduksi 1,1.1019 cm-3
dan rapat keadaan efektif hole dalam pita valensi 0,51.1019 cm-3 dalam Ge pada
suhu kamar. Jika diambil harga Eg=0,7 eV, maka hitunglah


5 SEMIKONDUKTOR 153

a. massa efektif me dan mh untuk elektron dan hole!
b. konsentrasi pembawa muatan pada suhu kamar!
c. konsentrasi pembawa muatan pada suhu 77 K, jika dianggap energi celah tidak
bergantung pada suhu!
05. Galium Arsenit mempunyai konstanta dielektrik 10,4, massa efektif elektron
me=0,07mo dan hole mh=0,09mo.
a. Tentukan energi ionisasi donor dan aseptor!
b. Hitunglah radius Bohr untuk ikatan elektron donor dan hole aseptor!
06. Suatu sampel silikon didoping dengan donor arsen 1,0.1023 m-3. Sampel disimpan
dalam keadaan suhu kamar. Data untuk Si adalah Eg=1,1 eV, me=0,7mo dan
mh=mo.
a. Hitunglah konsentrasi elektron intrinsik, dan tunjukkan bahwa harga tersebut
dapat diabaikan bila dibandingkan dengan konsentrasi elektron sumbangan
donor!
b. Jika dianggap semua ketidakmurnian mengalami ionisasi, maka tentukan
posisi tingkat energi Fermi!
c. Bagaimana pengaruhnya terhadap tingkat energi Fermi jika terhadap sampel di
atas didopingkan aseptor sebanyak 6,0.1021 m-3?
07. Data untuk Si adalah μe=1350 cm2/Vs, μh=475 cm2/Vs, Eg=1,1 eV, me=0,7mo dan
mh=mo. Hitunglah konduktivitas intrinsik σ pada suhu kamar!
08. Turunkan persamaan (5.15) dan (5.16)!
09. Untuk Ge didapatkan εr=15,8 dan me/mo=0,1. Hitunglah jari-jari orbit keadaan
dasar dan energi ionisasi donor yang didopingkan ke dalam Ge!


B A B VI
BAHAN DIELEKTRIK

Bab ini membahas sifat dielektrik bahan, yang disertai dengan sifat optik dan
perubahan fasa bahan. Sifat tersebut meliputi rentang frekuensi yang sangat lebar,
yakni mulai dari daerah statik sampai ultraviolet, dan memberikan informasi penting
yang berkaitan dengan struktur bahan.
Bab ini diawali oleh bahasan rumusan dasar sifat dielektrik bahan.
Selanjutnya, dibahas konstanta dielektrik bahan sebagai besaran makroskopis, dan
merelasikannya dengan polarisabilitas molekul sebagai besaran mikroskopis. Sumber
polarisasi molekul adalah polarisabilitas polar, ionik dan elektronik. Akhirnya, bab
ini ditutup oleh bahasan gejala piezoelektrik dan ferroelektrik, dimana keduanya
berkaitan dengan polarisabilitas ionik

6.1 RUMUSAN DASAR POLARISASI BAHAN

Dua muatan listrik berlawanan, tetapi besarnya sama, yakni –q dan +q,
membentuk dipol listrik yang momennya
p = qd (6.1)

dengan d adalah vektor posisi dari muatan negatip ke positip, seperti ditunjukkan
oleh Gambar 6.1 berikut.

Gambar 6.1 Sebuah dipol listrik

6 BAHAN DIELEKTRIK 155

Suatu dipol listrik menimbulkan medan listrik di sekitarnya, yaitu
1 3( p • r )r − r 2 p
εr = (6.2)
4π ∈o r5
dengan r adalah vektor jarak yang menghubungkan dipol dengan titik medan yang
ditinjau. Ungkapan medan (6.2) di atas mengasumsikan bahwa r>>d.
Menempatkan suatu dipol dalam medan listrik eksternal ε o , menyebabkan

timbulnya torsi pada dipol, yaitu
τ = p ×εo (6.3)

seperti ditunjukkan oleh Gambar 6.2 berikut.

Gambar 6.2 Torsi pada suatu dipol yang ditimbulkan oleh medan listrik luar
Torsi berusaha membawa dipol menjadi searah medan. Disamping itu, interaksi
antara dipol dan medan menimbulkan energi potensial
V = − p • ε o = − pε o cosθ (6.4)

Tampak bahwa dipol memiliki energi potensial minimum bila orientasinya paralel
medan. Hal ini sesuai dengan kecenderungan torsi pada dipol seperti di atas.
Dalam bahan dielektrik, kumpulan momen dipol membentuk polarisasi P ,
yakni jumlah momen dipol persatuan volume. Untuk suatu kristal, polarisasi
merupakan jumlah momen dipol dalam suatu sel satuan dibagi dengan volume sel.
Jika bahan mengandung jumlah molekul persatuan volume sebanyak N, dan masing-
masing memiliki momen p , serta momen tersebut searah, maka polarisasinya

P=N p (6.5)



6.2 KONSTANTA DIELEKTRIK BAHAN (PANDANGAN
MAKROSKOPIS)
Bahan dielektrik yang ditempatkan dalam suatu medan listrik eksternal ε o

mengalami perpindahan listrik

D =∈o ε o (6.6)

dengan ∈o adalah permitivitas vakum. Disamping itu, bahan menjadi terpolarisasi,

sehingga sifat elektromekaniknya berubah melalui ungkapan
D =∈o ε + P (6.7)

dengan ε adalah medan listrik dalam bahan. Gabungan kedua persamaan (6.6) dan
(6.7) di atas menghasilkan
1
ε = εo − P (6.8)
∈o
Tampak bahwa polarisasi bahan menyebabkan terjadinya induksi medan. Hal ini
dijelaskan dalam Gambar 6.3 berikut.

εo

ε ε'
+ -
+ - + - + - + - + -
+ - + - + - + - + -
+ - + - + - + - + -
+ - + - + - + - + -
+ - + - + - + - + -

Gambar 6.3 Medan ε ' melawan medan luar ε o . Resultan medan internal adalah ε

Polarisasi menyebabkan terjadinya muatan polarisasi pada permukaan bahan, yakni
muatan positip di sebelah kanan dan negatip di kiri. Muatan ini menimbulkan medan
listrik ε ' yang arahnya ke kiri melawan medan luar ε o . Akibatnya medan internal

resultan, yakni ε lebih kecil daripada ε o .



Suseptibilitas listrik χ bahan didefinisikan oleh hubungan

P =∈o χ ε (6.9)
Hubungan (6.9) berlaku untuk bahan dielektrik linier isotropik, misalnya bahan kubik
dan amorf. Substitusi polarisasi (6.9) ke dalam perpindahan listrik (6.7) di atas
menghasilkan
D =∈o ε + ∈o χ ε =∈o (1 + χ )ε =∈o ∈r ε =∈ ε (6.10)

dengan ∈ = permitivitas listrik (mutlak)
∈r = permitivitas listrik relatif (terhadap ∈o ) = konstanta dielektrik

Konstanta dielektrik ∈r dan suseptibilitas listrik χ merupakan besaran karakteristik
makroskopis bahan.

6.3 POLARISABILITAS BAHAN (PANDANGAN MIKROSKOPIS)
6.3.1 Persamaan Clausius-Mosotti
Polarisasi bahan, yakni pensejajaran momen dipol molekul, terjadi karena
medan listrik. Oleh karena itu diambil asumsi bahwa momen dipol molekul p
sebanding dengan medan listrik lokal ε l pada molekul yang bersangkutan

p = α εl (6.11)

dengan α adalah polarisabilitas molekul.
Untuk memperoleh ε l dipergunakan perumusan Lorentz, yaitu suatu dipol

tertentu dibayangkan dikelilingi oleh rongga bola yang berjari-jari R cukup besar
sehingga titik-titik di permukaan bola luar dapat dianggap sebagai medium kontinu.
Medan lokal yang bekerja pada dipol di pusat bola
ε l = ε o + ε1 + ε 2 + ε 3 (6.12)

dimana
ε o = medan eksternal
ε 1 = medan yang terjadi karena muatan polarisasi pada permukaan eksternal bahan
ε 2 = medan yang terjadi karena muatan polarisasi pada permukaan bola Lorentz
ε 3 = medan yang terjadi karena semua dipol dalam bola Lorentz



Bagian antara bola dan permukaan eksternal menghasilkan muatan total nol karena
muatan polarisasinya saling menetralkan satu sama lain. Pada ungkapan (6.12) di
atas, ε o dan ε 1 merupakan medan makroskopis. Hal di atas ditunjukkan oleh

Gambar 6.4 berikut.

+ -
- + +
+ -
- + +
+ + -
- + θ +
+ -
- + +
+ εl -
- + +
+ + + -
- +
+ -

Gambar 6.4 Prosedur menghitung ε l pada dipol yang terletak pada pusat bola Lorentz

Medan ε 1 . Medan ini dikenal sebagai medan depolarisasi karena arahnya melawan
medan eksternal ε o . Untuk bahan berbentuk keping tak berhingga, dengan

menggunakan hukum Gauss, nilai medan ini
1
ε1 = − P (6.13)
∈o

Medan ε 2 . Karena bola cukup besar, maka muatan polarisasi pada permukaan
rongga Lorentz dapat dianggap memiliki distribusi kontinu dengan kerapatan
n • P = P cosθ
ˆ
ˆ
dengan n adalah normal (arah keluar) permukaan bola. Elemen luas permukaan bola
dS = R2 sin θ dθ dφ. Medan yang ditimbulkan oleh muatan ini adalah
π 2π
1 ⎛ P cosθ ⎞
ε2 = ∫ φ∫ ⎜ ⎟ cosθ R sin θ dθ dφ
2
(6.14)
4π ∈o θ=0 ⎝
=0 R 2
⎠

Faktor cos θ muncul karena integrasi hanya mengambil medan sepanjang arah P
(komponen lain lenyap karena simetri). Hasil integrasi di atas
1
ε2 = P (6.15)
3 ∈o



Medan ε 3 . Dipol dalam bola berdistribusi secara diskrit dan masing-masing
menimbulkan medan listrik (persamaan (6.2)) di sekitarnya. Oleh karena itu medan
total diperoleh dengan menjumlahkan seluruhnya. Medan total ini bergantung pada
struktur kristal bahan. Untuk bahan berstruktur kubik, nilai medan total ini adalah
nol. Jadi
ε3 = 0 (6.16)

Dengan demikian substitusi medan (6.13), (6.15) dan (6.16) ke dalam (6.12)
menghasilkan medan lokal
2
εl = εo − P (6.17)
3 ∈o
Bila ditulis dalam bentuk medan makroskopis bahan dielektrik ε , dengan
menggunakan persamaan (6.8), maka ungkapan medan lokal (6.17) di atas menjadi
1
εl = ε + P (6.18)
3 ∈o

Tampak bahwa medan lokal ε 1 lebih besar dari medan rata-rata ε . Ungkapan (6.18)
sering dinamakan hubungan Lorentz.
Medan Maxwell, ε , merupakan besaran makroskopis dan medan konstan
rata-rata dari seluruh jumlah molekul. Sedangkan medan Lorentz, ε 1 , merupakan
besaran mikroskopis yang nilainya berfluktuasi, yaitu sangat besar pada tempat di
sekitar molekul. Oleh sebab itu, molekul akan lebih efektif terpolarisasi dalam ε 1
daripada dalam ε . Hal ini dilukiskan dalam Gambar 6.5 berikut.

Gambar 6.5 Perbedaan antara medan Maxwell ε dan medan Lorentz ε 1 .
Bulatan padat adalah molekul



Substitusi medan lokal (6.18) ke dalam persamaan (6.5) melalui persamaan
(6.11) menghasilkan polarisasi bahan dielektrik
Nα
P= (6.19)
Nα
1−
3 ∈o

Sedangkan substitusi polarisasi (6.19) ke dalam perpindahan listrik (6.7)
menghasilkan ungkapan konstanta dielektrik
2
1+ Nα
3 ∈o
∈r = (6.20)
Nα
1−
3 ∈o

Hasil ini menunjukkan bahwa besaran makroskopis ∈r dapat diungkapkan dalam
bentuk besaran mikroskopis α. Ungkapan konstanta dielektrik (6.20) di atas
seringkali ditulis dalam bentuk
∈r −1 Nα
= (6.21)
∈r +2 3 ∈o
dan disebut sebagai hubungan Clausius-Mosotti. Bentuk (6.21) di atas dapat juga
ditulis menjadi

W ⎛ ∈r −1 ⎞ N Aα
⎜ ⎟= (6.22)
ρ ⎜ ∈r +2 ⎟ 3 ∈o
⎝ ⎠
Hal ini menunjukkan bahwa polarisabilitas α dapat ditentukan asalkan besaran berat
molekul W, rapat massa ρ, dan konstanta dielektrik ∈r diketahui. Ungkapan ruas
kanan (dan ruas kiri) dalam (6.22) di atas dinamakan polarisabilitas molar.
Persamaan Clausius-Mosotti cukup valid untuk bahan muatan dan cairan.
N Aα
Untuk gas, dimana N kecil, penyebut (6.20) menunjukkan << 1 sehingga dapat
3 ∈o
dideretkan. Bila dari deret tersebut diambil orde pertama, maka diperoleh ungkapan
konstanta dielektrik
Nα
∈r = 1 + (6.23)
∈o



Hal ini berarti, untuk gas, medan lokal ε 1 lebih kurang berharga sama dengan medan
rata-rata ε bahan.

6.3.2 Sumber Polarisabilitas
Sehubungan dengan proses polarisasi bahan, struktur molekul/atom yang
membangun suatu bahan dapat dikelompokkan menjadi berikut.
a. Molekul polar, yakni molekul yang mempunyai resultan momen dipol permanen
tidak sama dengan nol. Contohnya H2O.
b. Molekul nonpolar, yakni molekul yang mempunyai resultan momen dipol
permanen sama dengan nol. Contohnya CO2.
c. Molekul ionik, yakni molekul yang berikatan ionik. Contohnya NaCl.
d. Atom kristal kovalen bersifat nonpolar dan nonionik. Contohnya Si dan Ge.

Berdasarkan jenis molekul/atom di atas dan perilakunya saat dikenakan medan, maka
polarisabilitas bahan dapat terdiri dari beberapa jenis sebagai berikut.
a. Polarisabilitas polar/orientasional (αp)
Momen dipol permanen bahan terdistribusi secara acak sehingga polarisasi sama
dengan nol. Saat dikenakan medan momen dipol cenderung mensejajarkan diri
terhadap arah medan sehingga polarisasi tidak sama dengan nol.
b. Polarisabilitas ionik (αi)
Medan menyebabkan ion positip bergerak searah medan dan ion negatip bergerak
berlawanan arah medan, sehingga panjang ikatan antarion menjadi longgar.
Perpindahan relatif ion bermuatan ini menghasilkan momen dipol dalam satuan
sel, yang sebelumnya tidak ada.
c. Polarisabilitas elektronik (αe)
Masing-masing ion atau atom dalam molekul terdiri dari inti (nukleus) dan
elektron. Bila dikenakan medan, maka ion atau atom individual tersebut menjadi
terpolarisasi karena elektron mengalami perpindahan relatif terhadap inti ke arah
yang berlawanan dengan arah medan. Hal yang sama terjadi juga pada atom netral.
Dari uraian di atas, umumnya, polarisabilitas total suatu bahan dapat ditulis



α = αe + αi + αp (6.24)
Bentuk αe terjadi pada semua jenis bahan. Sedangkan bentuk αi hanya terjadi pada
bahan ionik. Pada bahan polar dapat terjadi proses ketiga polarisasi di atas.
Terdapat ciri khusus yang membedakan satu sama lain dari ketiga polarisasi di
atas, yakni sebagai berikut.
a. Polarisasi polar menunjukkan kebergantungan yang kuat terhadap suhu, sedangkan
dua yang lain tidak. Konstanta dielektrik bahan polar mengalami penurunan
dengan naiknya suhu.
b. Perilaku polarisabilitas bolak-balik, yakni saat pada bahan dikenakan medan listrik
bolak-balik, seperti ditunjukkan pada Gambar 6.6 berikut.

Gambar 6.6 Sketsa polarisabilitas total α terhadap frekuensi ω dalam bahan polar

Terlihat bahwa pada ω>ωp (p=polar), sumbangan αp menghilang karena dipol
tidak mampu mengikuti gerakan medan yang berosilasi sedemikian cepatnya
sehingga dipol dalam keadaan stasioner. Pada daerah ω>ωi (i=ionik), ion dengan
massa yang berat tidak sanggup untuk mengikuti osilasi medan yang sangat cepat
sehingga polarisabilitas αi sama dengan nol; dan pada daerah ini hanya terdapat
polarisabilitas elektronik αe saja. Tetapi pada ω>ωe (e=elektronik), αe sama
dengan nol karena elektron terlalu berat untuk mengikuti medan yang berosilasi



sangat cepat. Dengan demikian konstanta dielektrik bahan polar menurun dengan
kenaikan frekuensi dari daerah statik sampai ke optik.
6.3.2.1 Polarisabilitas Polar
6.3.2.1.1 Polarisabilitas Polar Statik
Semula, momen dipol mempunyai orientasi acak sehingga resultan polarisasi
rata-rata bahan sama dengan nol. Bila pada bahan dikenakan medan listrik, misalnya
ε, maka energi potensial dipol sama seperti persamaan (6.4), yakni
V = − p • ε = − pε cosθ (6.25)
dengan θ adalah sudut antara arah dipol dan medan. Medan menyebabkan adanya
torsi dan distribusi dipol tidak lagi acak, melainkan cenderung mensejajarkan diri
dalam arah medan. Probabilitas untuk mendapatkan dipol dalam arah θ memenuhi
fungsi distribusi Maxwell-Boltzmann
f (θ ) = e −V / koT = e pε cosθ / koT (6.26)
Terlihat bahwa dipol lebih menyukai arah θ=0o, yakni searah medan.
Harga rata-rata dipol dalam arah-X

px =
∫ p f (θ )dΩ
x
(6.27)
∫ f (θ )dΩ
dimana integrasi dilakukan atas semua arah dipol dalam sudut ruang Ω. Dalam hal ini
px = p cos θ θ = (0 s/d π) dΩ = sin θ dθ dφ dan φ = (0 s/d 2π)
Hasil integrasi di atas adalah
p x = p L(u ) (6.28)

dengan L(u) = coth u – 1/u dan u = pε/koT. Fungsi Langevin L(u) mempunyai bentuk
sketsa seperti ditunjukkan dalam Gambar 6.7 berikut.



L(u)

1

u= ( pε
k oT
)
3

Gambar 6.7 Fungsi Langevin L(u) terhadap u
Pada suhu kamar dan medan yang sedang, u<<1 dan fungsi naik secara linier dan
dengan mengekspansikan coth (u) dapat diperoleh L(u)≅(1/3)u. Sedangkan untuk
suhu tinggi dan medan yang sangat besar, u>>1 fungsi mempunyai harga saturasi,
yakni L(u)=1, sehingga semua dipol berdistribusi searah medan.
Untuk kebanyakan eksperimen, diambil pendekatan medan yang sedang,
sehingga
p2
px = ε (6.29)
3k oT
Terlihat bahwa momen berbanding lurus dengan medan dan berbanding terbalik
dengan suhu. Dengan demikian polarisabilitas polarnya
p2
αp = (6.30)
3k oT
Substitusi harga polarisabilitas polar (6.30) ke dalam persamaan Clausius-Mosotti
(6.22) menghasilkan
W ⎛ ∈r −1 ⎞ N A ⎛ p2 ⎞
⎜ ⎟= ⎜α ei + ⎟ (6.31)
ρ ⎜ ∈r +2 ⎟ 3 ∈o ⎜
⎝ ⎠ ⎝ 3k oT ⎟
⎠
dengan αei adalah kombinasi polarisabilitas elektronik dan ionik yang tidak
bergantung suhu. Dengan menggrafikkan polarisabilitas molar (ruas kiri) terhadap
kebalikan suhu 1/T, maka dapat ditentukan momen dipol permanen molekul polar p
dan polarisabilitas nonpolar αei suatu bahan. Untuk molekul nonpolar, grafik tersebut
berbentuk horisontal.



6.3.2.1.2 Polarisabilitas Polar Bolak-balik

Dalam mengikuti osilasi medan listrik, dipol mengalami gesekan karena
bertumbukan dengan molekul lain dalam sistem. Penyerapan energi medan ini
menimbulkan panas. Hal ini sering disebut “dielectric loss”.
Gerakan polarisasi polar digambarkan oleh persamaan
dp d (t ) 1
= {p ds (t ) − p d (t )} (6.32)
dt τ
dengan pd(t) = momen dipol polar pada saat t
pds(t) = momen dipol saturasi (setimbang)
τ = waktu relaksasi
Misalnya, medan listrik statik dikenakan pada t=0. Dalam hal ini pds(t) =αpε=po,
dimana αp adalah polarisabilitas polar statik dan po adalah momen dipol permanen
molekul. Oleh karena itu persamaan di atas menjadi
dp d (t ) p d (t ) p o
+ = (6.33)
dt τ τ
yang mempunyai solusi
pd(t) = po (1 – e-t/τ) (6.34)
Jika medan listrik statik dikenakan cukup lama pada bahan sehingga dicapai nilai
setimbang po, dan tiba-tiba medan dihentikan pada t=0, maka pds=0 dalam persamaan
(6.32) sehingga solusinya adalah
pd(t) = po e-t/τ (6.35)
Untuk medan listrik bolak-balik
ε(t) = A e-iωt (6.36)
keadaan setimbangnya dinyatakan oleh
pds(t) = αp(0) ε(t) (6.37)
dengan αp(0) adalah polarisabilitas polar statik; dan persamaan geraknya dinyatakan
oleh
dp d (t ) p d (t ) α p (0)
+ = ε (t ) (6.38)
dt τ τ



Diambil solusi berbentuk
ps(t) = αp(ω) ε(t) = αp(ω) A e-iωt (6.39)
dengan αp(ω) adalah polarisabilitas bolak-balik. Substitusi bentuk solusi (6.39) ke
dalam persamaan gerak (6.38) menghasilkan
α p (0)
α p (ω ) = (6.40)
1 − iω τ

Terlihat bahwa polarisabilitas αp(ω) merupakan besaran komplek, artinya polarisasi
tidak sefasa dengan medan. Hal ini berarti terjadi absorbsi energi.
Bila kontribusi ionik cukup kecil sehingga dapat diabaikan, maka konstanta
dielektrik ∈r (ω ) dapat ditulis
∈r (ω ) = 1 + χ e (ω ) + χ p (ω )

dengan χ e (ω ) dan χ p (ω ) , masing-masing adalah suseptibilitas elektronik dan polar.

Dalam dispersi polar, yakni daerah gelombang mikro, suseptibilitas elektronik relatif
konstan, sehingga kontribusi polar dapat ditulis
∈r (ω ) = n 2 + χ p (ω ) (6.41)

dengan n 2 = 1 + χ e (ω ) = konstanta dielektrik optik
n = indek bias
Kontribusi polar χ p (ω ) tidak sepenuhnya mampu mengikuti osilasi medan sehingga

terjadi keterlambatan fasa. Karena χ p sebanding dengan αp, maka χ p (ω )

merupakan besaran komplek yang bentuknya sama dengan αp(ω) dalam (6.40)
sehingga konstanta dielektrik (6.40) dapat ditulis
χ p (0)
∈r (ω ) = n 2 + (6.42)
1 − iω τ

dengan χ p (0) =∈r (0) − n 2 adalah suseptibilitas polar statik. Terlihat bahwa

konstanta dielektrik (6.42) di atas bergantung pada frekuensi. Hal ini berarti bahan
menunjukkan gejala dispersi. Dalam bentuk bagian riil dan imaginer, konstanta
dielektrik ∈r (ω ) dapat ditulis



∈r (ω ) =∈'r (ω ) + i ∈" (ω )
r (6.43)
dengan
∈r (0) − n 2
∈'r (ω ) = n 2 + (6.44a)
1 + ω 2τ 2
⎛ ∈r (0) − n 2 ⎞
∈ (ω ) = ⎜
"
r ⎜ 1 + ω 2τ 2 ⎟ω τ
⎟ (6.44b)
⎝ ⎠
Ungkapan (6.44) ini disebut persamaan Debye, yang secara grafik ditunjukkan oleh
Gambar 6.8 berikut.

Gambar 6.8 Sketsa bagian riil ∈r (ω ) dan bagian imaginer ∈r (ω )
' "

terhadap ln ωτ untuk bahan polar

Terlihat bahwa grafik ∈'r (ω ) − ln ω τ merupakan kurva dispersi; dan ∈" (ω ) − ln ω τ
r

kurva absorbsi. Bagian riil ∈'r (0) berharga konstan, yakni ∈r (0) pada daerah
ω<<1/τ, dan berharga n2 (konstanta dielektrik frekuensi tinggi) pada daerah ω>>1/τ.
Besaran 1/τ sering disebut frekuensi tumbukan, yang mencakup semua frekuensi
sampai dengan daerah gelombang mikro. Sedangkan bagian imaginer ∈" (ω )
r

mencapai harga maksimum, yakni 1
2
{∈
r }
(0) − n 2 , pada ω=1/τ.

6.3.2.2 Polarisabilitas Ionik
Kristal ionik diatomik satu dimensi ditunjukkan dalam Gambar 6.9 berikut.



2n 2n+1
+ - + -

M2 M1

Gambar 6.9 Kisi ionik diatomik satu dimensi
Dalam satuan sel terdapat dua atom, masing-masing dengan massa M1 dan M2 dan
muatan listrik e* dan –e*. Muatan efektif e* lebih kecil daripada muatan elektron e
karena transfer elektron dalam ikatan ionik molekul tidak sempurna. Jika medan
listrik bolak-balik ε dikenakan terhadap kristal, persamaan gerak masing-masing ion
adalah
∂ 2U 2 n +1
M1 = −α {2U n +1 − U 2 n − U 2 n + 2 } + e * ε (6.45)
∂t 2
∂ 2U 2 n
M2 = −α {2U 2 n − U 2 n −1 − U 2 n +1 } − e * ε (6.46)
∂t 2
Terlihat bahwa kristal mengalami gaya interaksi antaratom dan gaya listrik. Hal ini
berarti kisi mengalami vibrasi yang dipaksakan.
Misalnya, medan ε berbentuk gelombang bidang
ε = εx ei(kx - ωt) (6.47)
Jika diasumsikan λ>>d (atau k→0), maka semua atom sejenis mempunyai
perpindahan yang sama. Dalam keadaan mapan, M1 dan M2 masing-masing
mempunyai perpindahan U+ dan U- yang berbentuk sama seperti medan gaya (6.47)
U+ = Uo+ e-iωt (6.48a)
U- = Uo- e-iωt (6.48b)
Dengan harga k=0. Substitusi (6.47) dan (6.48) ke dalam persamaan gerak (6.45) dan
(6.46) di atas menghasilkan perpindahan ionik
⎛ e* ⎞
U o+ = ⎜ 2
⎟
⎜ M (ω − ω ) ε
2 ⎟ x
(6.49)
⎝ 1 t ⎠
⎛ e* ⎞
U o − = −⎜ ⎟ε x (6.50)
⎝ 2 t (
⎜ M ω 2 −ω 2 ) ⎟
⎠



⎛ 1 1 ⎞
dengan ω t2 = 2α ⎜
⎜M + M ⎟ . Tampak bahwa ωt adalah frekuensi fonon optik
⎟
⎝ 1 2 ⎠
transversal pada k=0. Perbedaan perpindahan kedua ion ini menyebabkan timbulnya
momen dipol listrik molekul. Dengan demikian polarisasi ionik Pi yang terjadi
Pi = N e* (Uo+ -Uo-) (6.51)
Selain itu, pada kristal terjadi juga polarisasi elektronik Pe.
Polarisasi total Pie (ionik dan elektronik) disubstitusikan ke dalam persamaan
(6.7) sehingga menghasilkan konstanta dielektrik
Pe N (e*) 2 1
∈r (ω ) = 1 + + (6.52)
∈o ε ∈o ω t2 μ ω2
1− 2
ωt
M 1M 2
dengan μ = adalah massa tereduksi kedua ion. Pada ruas kanan, suku
M1 + M 2
kedua merupakan kontribusi elektronik, dan suku ketiga kontribusi ionik.
Untuk ω<<ωt, kedua kontribusi ada dan membentuk fungsi dielektrik statik ∈r (0) .

Untuk ω>>ωt, kontribusi ionik menjadi nol.
Konstanta dielektrik pada frekuensi tinggi, yang hanya terdiri dari kontribusi
elektronik, disimbolkan dengan ∈r (∞) = n 2 , dengan n adalah indek bias optik.
Dengan demikian ungkapan konstanta dielektrik (6.52) di atas dapat ditulis dalam
bentuk
∈r (0) − n 2
∈r (ω ) = n 2 + (6.53)
ω2
1− 2
ωt
Suku kedua ruas kanan merupakan polarisabilitas ionik bolak-balik, dan besaran
∈r (0) − n 2 = χ i (0) merupakan suseptibilitas ionik statik. Sketsa ∈r (ω ) terhadap ω

disajikan dalam Gambar 6.10 berikut.



∈r (ω )

∈r (0)
n2

0 ω
ωt ωl

Gambar 6.10 Sketsa konstanta dielektrik ∈r (ω ) terhadap ω molekul ionik

Pada gambar di atas tampak bahwa ∈r (ω ) <0 dalam rentang ωt<ω<ωl, dengan ωl

adalah frekuensi dimana ∈r (ω ) =0.
Fungsi konstanta dielektrik dapat digunakan untuk mempelajari sifat optik
medium. Jika indek bias optik berbentuk komplek, maka konstanta dielektrik dapat
dituliskan dalam bentuk
∈r = (n + i Χ )
2
(6.54)
dengan Χ adalah koefisien pemadaman. Refleksivitas R dan absorbsi medium αab
diungkapkan melalui hubungan

R=
(n − 1)2 + Χ 2 (6.55)
(n + 1)2 + Χ 2
α ab = 2Χk (6.56)

Jika ∈r (ω ) <0, maka menurut (6.54) haruslah n=0 dan Χ ≠ 0 , sehingga refleksivitas
(6.55) berharga R = 1. Hal ini berarti gelombang datang dengan frekuensi dalam
rentang ωt<ω<ωl mengalami refleksi total, dan tidak dapat merambat dalam kristal.
Daerah ini disebut celah terlarang.
Pada gambar di atas tampak pula bahwa ∈r (ω ) menunjukkan dispersi yang
kuat ( ∈r (ω ) →∞) di dekat frekuensi fonon optik ωt. Di daerah ini, disamping terjadi
absorbsi maksimum, juga terjadi kondisi resonansi, yakni dimana frekuensi sinyal
sama dengan frekuensi alami sistem ionik sehingga respon sistem menjadi tak



berhingga. Absorbsi dan refleksi optik secara kuat di atas terjadi dalam daerah
inframerah.

6.3.2.3 Polarisabilitas Elektronik
6.3.2.3.1 Polarisabilitas Elektronik Statik
Dengan asumsi distribusi elektron uniform di sekitar atom, dikenakannya
medan ε pada atom, melalui hukum elektrostatik, menyebabkan inti mengalami
perpindahan terhadap pusat atom sebesar
⎛ 4π ∈o ra3 ⎞
x=⎜
⎜ Ze ⎟ε
⎟ (6.57)
⎝ ⎠
dengan ra adalah radius atom dan Ze adalah muatan inti. Dengan demikian atom
terpolarisasi dengan momen dipol
P=Zex
sehingga polarisasi elektronik yang terjadi
α e = 4π ∈o ra3 (6.58)

6.3.2.3.2 Polarisabilitas Elektronik Bolak-balik
Dalam hal ini diasumsikan bahwa elektron dalam atom mengalami gaya pulih
elastik yang bersesuaian dengan frekuensi resonansi ωo. Persamaan gerak elektron
saat dikenakan medan bolak-balik dengan polarisasi dalam arah-X
d 2x
m + mω o x = −e ε
2
(6.59)
dt 2
Jika medan ε = εx e-iωt, maka dapat ditentukan solusi untuk perpindahan x dan
polarisasi P. Polarisabilitas elektronik yang diperoleh
e2 / m
α e (ω ) = 2 (6.60)
ωo − ω 2
Jika terdapat Z elektron peratom dan N atom persatuan volume, maka suseptibilitas
listriknya



NZe 2 1
χ e (ω ) = (6.61)
∈o m ω o − ω 2
2

dan indek refraksi
NZe 2 1
n 2 (ω ) = 1 + (6.62)
∈o m ω o − ω 2
2

Secara grafik n2(ω) terhadap ω disajikan dalam Gambar 6.11 berikut.

n 2 (ω )

n 2 (0)
1

ω
0
ωo

Gambar 6.11 Sketsa kuadrat indek bias n2(ω) terhadap ω

Tampak bahwa dispersi tajam terjadi pada frekuensi resonansi ωo (daerah ultraviolet).
Jika kita memulai ωo=0, maka elektron berperilaku sebagai partikel bebas. Pada
frekuensi tinggi, ωo<<ω, harga n2(ω)→1, seperti halnya untuk vakum. Pada frekuensi
ini elektron tidak mampu mengikuti osilasi medan yang kuat.

6.4 GEJALA PIEZOELEKTRIK
Gejala piezoelektrik berkait dengan polarisasi ionik. Efek langsung
piezoelektrik menunjukkan bahwa bila pada kristal terjadi regangan, maka akan
terjadi pula medan listrik. Sedangkan efek balik, pemakaian medan listrik
menghasilkan regangan . Dengan demikian, gejala piezoelektrik dapat digunakan
untuk mengkonversikan energi listrik menjadi energi mekanik, atau sebaliknya,
seperti yang terjadi pada transduser.



Gejala piezoelektrik hanya terjadi pada bahan nonsentrosimetri. Pada bahan
sentrosimetri, distorsi yang terjadi juga bersifat sentrosimetri sehingga polarisasi nol,
seperti ditunjukkan oleh Gambar 6.12 berikut.

Gambar 6.12 Kristal sentrosimetri tidak menunjukkan efek piezoelektrik
Sedangkan dalam bahan nonsentrosimetri, distorsi menghasilkan polarisasi. Distorsi
menyebabkan terjadinya perpindahan muatan ionik dalam kristal, yang semula
berimpit, karena dikenakannya tekanan, seperti ditunjukkan oleh Gambar 6.13
berikut.

Gambar 6.13 Gejala piezoelektrik pada kwarsa

6.5 GEJALA FERROELEKTRIK
Umumnya, suseptibilitas ionik tak bergantung pada suhu. Tetapi, pada
kelompok bahan ferroelektrik konstanta dielektrik berubah terhadap suhu melalui
hubungan hukum Curie-Weiss
C
∈r = (6.63)
T − TC



dengan C adalah konstanta Curie dan TC adalah suhu Curie. Hal ini ditunjukkan

∈r

0 T
TC

Gambar 6.14 Sketsa konstanta dielektrik ∈r terhadap suhu T dalam bahan ferroelektrik

Hubungan di atas berlaku bila T>TC. Dalam daerah ini, bahan berada dalam fasa
paraelektrik, yang mana polarisasi hanya dapat terjadi jika pada bahan dikenakan
medan eksternal dan polarisasinya lenyap bila medan dihilangkan.
Dalam daerah T<TC, bahan menjadi terpolarisasi secara spontan. Dalam
daerah ini bahan berada dalam fasa ferroelektrik. Dengan demikian, suhu Curie TC
merupakan tempat transisi fasa. Polarisasi spontan PS semakin naik bila suhu turun,
seperti ditunjukkan dalam Gambar 6.15 berikut.

PS

0 T
TC

Gambar 6.15 Sketsa polarisasi spontan PS terhadap suhu T dalam bahan ferroelektrik
Dalam fasa ferroelektrik, pusat muatan positip kristal tidak berimpit dengan pusat
muatan negatip. Gejala ferroelektrik hanya terjadi pada kelas nonsentrosimetri polar.
Arah polarisasi spontan ferroelektrik tidak sama dalam keseluruhan bagian
bahan. Oleh karena itu bahan terdiri dari sejumlah domain, yakni daerah dimana



polarisasinya konstan. Domain berbeda mempunyai polarisasi berbeda pula sehingga
polarisasi total bahan menjadi nol saat setimbang. Pensejajaran domain terjadi bila
dikenakan medan listrik eksternal; yakni domain yang polarisasinya searah medan
bertambah banyak, dan sebaliknya. Polarisasi ini dapat dibalik oleh medan listrik
dalam arah sebaliknya. Dengan demikian bahan ferroelektrik menunjukkan loop
histerisis, seperti ditunjukkan oleh Gambar 6.16 berikut.

Gambar 6.16 Loop histerisis bahan ferroelektrik
Contoh bahan ferroelektrik adalah jenis perovskit, misalnya barium titanat
(BaTiO3). Di atas suhu Curie (TC=120oC), BaTiO3 berstruktur kubik, seperti
ditunjukkan oleh Gambar 6.17 berikut.



=Ba2+

=O2-

=Ti4+

Gambar 6.17 Struktur BaTiO3 dalam fasa kubik
Tetapi, di bawah suhu Curie strukturnya berubah menjadi tetragonal. Dalam fasa ini,
ion Ti4+ dan O2- bergeser terhadap ion Ba2+, seperti ditunjukkan oleh Gambar 6.18
berikut.

a=b=0,398 nm
=Ti4+

c=0,403 nm =O2-

0,006 nm
0,006 nm

Gambar 6.18 Pergeseran Ti4+ dan O2- terhadap Ba2+ pada tetragonal BaTiO3
Akibatnya, terjadilah pemisahan pusat muatan positip dan negatip sejauh 0,012 nm,
sehingga terjadi polarisasi spontan.

RINGKASAN



01. Dua muatan listrik berlawanan, tetapi besarnya sama, yakni –q dan +q,
membentuk dipol listrik yang momennya p. Suatu dipol listrik menimbulkan
medan listrik di sekitarnya. Jika suatu dipol dalam medan listrik eksternal, maka
timbul torsi dan energi potensial pada dipol. Dalam bahan dielektrik, kumpulan
momen dipol membentuk polarisasi, yakni jumlah momen dipol persatuan
volume.
02. Bahan dielektrik yang ditempatkan dalam suatu medan listrik eksternal ε o

mengalami perpindahan listrik D, bahan menjadi terpolarisasi P, dan terjadi
induksi medan ε. Hubungan antara P dan ε melahirkan suseptibilitas listrik χ, dan
antara D dan ε melahirkan konstanta dielektrik ∈r . Kedua besaran ini merupakan
besaran karakteristik makroskopis bahan.
03. Polarisasi bahan terjadi karena medan listrik. Diambil asumsi bahwa momen
dipol molekul p sebanding dengan medan listrik lokal ε l pada molekul yang

bersangkutan, yakni p = α ε l , dengan α adalah polarisabilitas molekul.
Untuk memperoleh ε l dipergunakan perumusan Lorentz, yaitu suatu dipol

tertentu dibayangkan dikelilingi oleh rongga bola yang berjari-jari R cukup besar
sehingga titik-titik di permukaan bola luar dapat dianggap sebagai medium
kontinu. Jika jumlah dipol molekul adalah N, maka didapatkan ungkapan
hubungan besaran makroskopis konstanta dielektrik ∈r dan besaran mikroskopis
∈r −1 Nα
polarisabilitas molekul α, yaitu = , yang disebut sebagai hubungan
∈r +2 3 ∈o

Clausius-Mosotti.
04. Sehubungan dengan proses polarisasi bahan, struktur molekul/atom yang
membangun suatu bahan dapat dikelompokkan menjadi molekul polar, nonpolar,
ionik, dan atom kristal kovalen bersifat nonpolar dan nonionik. Berdasarkan jenis
molekul/atom di atas dan perilakunya saat dikenakan medan, maka polarisabilitas
bahan dapat terdiri dari beberapa jenis, yaitu polarisabilitas polar/orientasional
(αp), ionik (αi), dan elektronik (αe). Oleh karena itu polarisabilitas total suatu



bahan dapat ditulis α = αe + αi + αp. Bentuk αe terjadi pada semua jenis bahan.
Sedangkan bentuk αi hanya terjadi pada bahan ionik. Pada bahan polar dapat
terjadi proses ketiga polarisasi di atas.
05. Polarisabilitas polar terdiri dari dua macam, yaitu statik dan bolak-balik. Jenis
p2
yang pertama menghasilkan α p = ; dan yang kedua menghasilkan
3k oT

α p (0)
α p (ω ) = yang merupakan besaran komplek, artinya polarisasi tidak
1 − iω τ
sefasa dengan medan (terjadi absorbsi energi). Pada jenis yang kedua juga
χ p (0)
didapatkan konstanta dielektrik ∈r (ω ) = 1 + χ e (ω ) + χ p (ω ) = n 2 + .
1 − iω τ
06. Pada frekuensi tinggi, yang hanya terdiri dari kontribusi elektronik, ungkapan
∈r (0) − n 2
konstanta dielektrik dapat ditulis dalam bentuk ∈r (ω ) = n 2 + . Suku
ω2
1− 2
ωt
kedua ruas kanan merupakan polarisabilitas ionik bolak-balik.
07. Polarisabilitas elektronik terdiri dari dua macam, yaitu statik dan bolak-balik.
Jenis yang pertama menghasilkan polarisasi elektronik α e = 4π ∈o ra3 . Sedangkan

e2 / m
jenis yang kedua menghasilkan polarisabilitas elektronik α e (ω ) = 2 .
ωo − ω 2
08. Gejala piezoelektrik berkait dengan polarisasi ionik dan hanya terjadi pada bahan
nonsentrosimetri. Gejala piezoelektrik dapat digunakan untuk mengkonversikan
energi listrik menjadi energi mekanik (efek balik), atau sebaliknya (efek langsung),
seperti yang terjadi pada transduser.
09. Pada kelompok bahan ferroelektrik konstanta dielektrik berubah terhadap suhu
C
melalui hubungan hukum Curie-Weiss ∈r = . Bila T>TC, polarisasi hanya
T − TC
dapat terjadi jika pada bahan dikenakan medan eksternal dan polarisasinya lenyap
bila medan dihilangkan (fasa paraelektrik); dan bila T<TC, bahan menjadi



terpolarisasi secara spontan (fasa ferroelektrik). Dalam fasa ferroelektrik juga
terdapat domain dan loop histerisis.

LATIHAN SOAL BAB VI
01. Bertolak dari medan lokal dalam persamaan (6.18), maka
a. Buktikan bahwa untuk bahan dielektrik linier isotropik medan lokal tersebut
dapat ditulis
⎛ χ⎞
ε l = ⎜1 + ⎟ε
⎝ 3⎠
b. Dari soal (a) buktikan bahwa suseptibilitas listrik bahan adalah
Nα / ∈o
χ=
Nα
1−
3 ∈o

(Ungkapan ini disebut hubungan Clausius-Mosotti antara suseptibilitas listrik
χ dan polarisabilitas molekul α)
c. Jika medan lokal sama dengan medan rata-rata dalam bahan, maka buktikan
bahwa suseptibilitas listrik soal (b) dapat ditulis
χ = Nα / ∈o
02. Di antara kedua plat kapasitor diisikan selenium amorf dengan konstanta
dielektrik 6,0 dan konsentrasi 3,67.1028 atom/m3.
a. Hitunglah polarisabilitas atomnya!
b. Hitunglah medan lokal pada atomnya, jika muatan plat menghasilkan medan
1500 V/m!
c. Hitunglah momen dipol atomnya dalam medan soal (b)!
d. Berapakah harga konstanta dielektriknya, jika medan lokal sama dengan medan
makroskopis?
03. Andaikanlah bahwa titik asal sistem koordinat bertempat pada pusat bola Lorentz
dan polarisasi dalam arah sumbu-Z, maka buktikan bahwa komponen medan ε2
(karena muatan polarisasi pada permukaan bola Lorentz) dalam arah sumbu-X dan
sumbu-Y berharga nol!



04. Momen dipol untuk distribusi muatan secara umum didefinisikan sebagai
p = ∑ qi ri , dengan qi dan ri , masing-masing adalah muatan dan vektor posisi
i

dari muatan ke-i, dan penjumlahan dilakukan atas semua muatan yang ada.
Pengambilan titik asal adalah sebarang.
a. Tunjukkan bahwa ungkapan di atas akan menjadi (6.1) bila hanya ada dua
muatan yang sama besar dan berlawanan tanda!
b. Buktikan bahwa jika muatan listrik sistem secara keseluruhan netral, maka
momen dipol tidak bergantung pada pengambilan titik asal!
05. Turunkanlah persamaan (6.13)!
06. Konstanta gaya untuk atom berdekatan dalam NaCl berharga 36 N/m. Jarak
setimbang kristal ini 2,82 Å.
a. Jika besar masing-masing muatan adalah e, maka hitunglah momen dipol pada
jarak setimbangnya!
b. Hitunglah perubahan jarak pisahnya karena medan listrik lokal 1500 V/m!
c. Hitunglah perubahan momen dipolnya!
d. Taksirlah polarisabilitas ionik statiknya!
07. Suatu kristal berstruktur kubik sederhana (dengan rusuk a) dan masing-masing
atomnya memiliki momen dipol sama, yaitu p .
a. Tunjukkan bahwa medan listrik pada suatu atom tertentu karena semua atom
yang berjarak a bernilai nol!
b. Ulangi soal (a) untuk medan dari semua atom yang berjarak a√2.
c. Ulangi soal (a) untuk medan dari semua atom yang berjarak a√3.
08. Suatu kristal berstruktur tetragonal sederhana (dengan sisi bujursangkar a dan
ketinggian c) dan masing-masing atomnya memiliki momen dipol p .
a. Tunjukkan bahwa medan listrik pada suatu atom tertentu karena semua atom
yang berjarak a adalah
1 p − 3 pZ z
ˆ
p1 =
2π ∈o a3
ˆ
dengan z adalah sumbu derajat-4 (tetrad)!


b. Tuliskan ungkapan medan yang dihasilkan semua atom yang berjarak c!
c. Tunjukkan bahwa resultan medan dari soal (a) dan (b) berharga nol bila c=a!
09. Polarisabilitas elektronik statik Na+ dan Cl-, masing-masing adalah 3,47.10-41
C2m/N dan 3,41.10-40 C2m/N. Sedangkan polarisabilitas ionik statik pasangan ion
NaCl adalah 3,56.10-40 C2m/N. NaCl berstruktur FCC dengan sisi 5,64 Å.
a. Dengan menggunakan hubungan Clausius-Mosotti, hitunglah konstanta
dielektrik NaCl!
b. Jika medan listrik 1500 V/m diarahkan tegak lurus sisi kubus, maka hitunglah
medan lokal pada pasangan ion! Hitung pula medan makroskopis dan medan
polarisasi dalam sampel!

10. Suatu bahan polar mempunyai konsentrasi molekul polar 1,6.1028 molekul/m3 dan
tiap molekul mempunyai momen dipol permanen 3,5.10-26 Cm. Dengan
menggunakan formulasi Langevin
a. hitunglah polarisasi saturasi!
b. hitunglah polarisasi pada 300 K dalam medan listrik 2,5.104 V/m!
c. Abaikan efek medan lokal dan hitunglah suseptibilitasnya pada 300 K!

11. Cahaya 500 nm diarahkan tegak lurus pada sampel dengan indek bias n=1,653
dan koefosien pemadaman Χ =2,35.10-2.
a. Hitunglah kecepatan gelombang dalam sampel!
b. Hitunglah panjang gelombang dalam sampel!
c. Hitunglah jarak dalam sampel sehingga intensitas gelombang tinggal
setengahnya, jika fraksi intensitas gelombang yang diteruskan
I = I o e −2 kΧz

dengan k = vektor gelombang datang
z = jarak tempuh gelombang dalam sampel
d. Hitunglah refleksivitasnya!
e. Hitunglah bagian riil dan imaginer konstanta dielektriknya!



12. Medan ε 3 dalam persamaan (6.12) karena dipol dalam rongga bola bergantung
pada simetri kristal, dan umumnya berharga tidak nol dalam kristal nonkubik.
Anggaplah bahwa medan ini berharga
b
ε3 = P
∈o

dengan b adalah konstanta, hitunglah konstanta dielektrik ∈r dalam bahan
tersebut!

13. a. Deretkanlah fungsi Langevin L(u) persamaan (6.28) dalam pangkat u, dan
tunjukkan bahwa
L(u) = u/3 – u3/45 + … , dimana u<<1
b. Hitunglah medan yang diperlukan untuk menghasilkan polarisasi dalam air
sebesar 10% polarisasi saturasi pada suhu kamar, jika diketahui polarisasi air
p=1,9.10-29 Cm!
14. Polarisabilitas molar air naik dari 4.10-5 menjadi 6,8.10-5 m3 jika suhu diturunkan
dari 500 K menjadi 300 K. Hitunglah momen permanen molekul air!
15. Ion Na+ dan Cl- dalam NaCl, masing-masing mempunyai polarisabilitas
elektronik 0,20.10-40 dan 2,65.10-40 farad m2. NaCl berstruktur FCC.
a. Hitunglah jarak terdekat antara atom Na dan Cl!
b. Hitunglah konstanta kisi NaCl!
16. Hitunglah polarisabilitas statik untuk atom hidrogen, jika diasumsikan bahwa
muatan pada elektron terdistribusi seragam dalam keseluruhan bola dengan jari-
jari Bohr!


B A B VII
BAHAN MAGNETIK

Bahan magnetik mempunyai banyak aplikasi, mulai dari teras penstransfer
dalam bidang kelistrikan sampai pada pita magnetik dalam bidang komputer. Oleh
karena itu, pengetahuan tentang sifat magnetik bahan banyak menarik minat para ahli
fisika, kimia dan teknik.
Bagian awal bab ini membahas perilaku magnetik dari atom bebas, dan
kemudian dilanjutkan dengan sifat magnetik elektron konduksi dalam logam.
Bahasan gejala ferromegnetik dibagi menjadi dua kelompok, yakni pada isolator dan
logam. Namun keduanya menitikberatkan pada bahasan medan magnet (internal)
molekuler yang berperan dalam gejala ferromagnetik. Akhirnya, bab ini ditutup oleh
bahasan tentang gejala antiferromagnetik dan ferrimagnetik.

7.1 SUSEPTIBILITAS MAGNETIK BAHAN

Pada bahan yang ditempatkan dalam medan magnet luar yang berintensitas
H , terjadi magnetisasi M , yakni momen dipol magnet persatuan volume. Untuk
kristal, magnetisasi merupakan momen dipol total dalam sel satuan tunggal dibagi
volume sel. Pada bahan, juga, terjadi induksi magnet B yang memenuhi hubungan
B = μo H + μo M (7.1)

Dengan demikian, induksi magnet dalam bahan terdiri dari dua bagian, yakni μ o H

karena sumber luar dan μ o M karena magnetisasi bahan.

Magnetisasi timbul karena medan luar. Untuk medan lemah M sebanding
dengan H (bahan isotropik linier)

7 BAHAN MAGNETIK 184

M =χ H (7.2)
dengan suseptibilitas magnetik χ sebagai tetapan pembandingnya. Asumsi tersebut
mengabaikan medan demagnetisasi, koreksi medan lokal dan lain-lain karena M
sangat kecil terhadap harga H (harga χ=M/H=10-5). Tetapi dalam bahasan
ferromagnetik, dimana M berharga besar, pengabaian ini ditiadakan. Dengan
mensubstitusikan M ke dalam (7.1) diperoleh
B = μ o (1 + χ ) H = μ H (7.3)

dengan μ=μo(1+χ) disebut permeabilitas bahan. Seringkali digunakan besaran
permeabilitas relatif
μ
μr = = 1+ χ (7.4)
μo
Berdasarkan tanda dan besar nilai suseptibilitas magnet suatu bahan
dikelompokkan menjadi sebagai berikut.
a. Bahan paramagnet, yang mempunyai harga χ positip dengan order 10-5 cm-3.
Berarti M paralel terhadap H . Contohnya, ion transisi dan ion tanah-jarang. Ion
ini mempunyai sel atomik yang tidak komplit.
b. Bahan diamagnet, yang mempunyai harga χ negatip dengan order 10-5 cm-3.
Berarti M berlawanan arah dengan H . Contohnya, kristal kovalen, ionik dan
atom gas mulia yang mempunyai sel penuh. Perilaku diamagnetiknya muncul
karena medan magnet menyebabkan distorsi gerakan orbitalnya.
c. Bahan ferromagnet, yang mempunyai harga χ besar sekali dengan order 105 cm-3
dan mengalami magnetisasi spontan di bawah suhu tertentu. Contohnya, logam Fe,
Co dan Ni.

7.2 GEJALA DIAMAGNETIK LANGEVIN

Perhatikanlah sebuah elektron beredar mengelilingi inti atom dalam medan
magnet B , seperti ditunjukkan dalam Gambar 7.1 berikut.



B

FL
inti
Fo
velektron

Gambar 7.1 Gejala awal diamagnetik atomik
Sebelum medan dikenakan, pada elektron bekerja gaya Coulomb
Fo = mω o r
2
(7.5)
dan terjadi momen magnetik elektron
e e
μ o = IA = π r 2 = ωor 2 (7.6)
T 2
Setelah medan dikenakan, pada elektron bekerja gaya lain, yakni gaya Lorentz
FL = −e(v × B) yang melawan arah gaya Coulomb. Dengan demikian, persamaan
gerak (7.5) berubah menjadi
Fo − eBr ω = mω 2 r (7.7)

yang merupakan persamaan kuadrat dalam ω. Jika medan kecil, maka bentuk
solusinya
eB
ω = ωo − (7.8)
2m
Tampak bahwa rotasi elektron lebih pelan. Reduksi frekuensi ini menimbulkan
perubahan momen magnetik, bertolak dari (7.6), yaitu
⎛ e2r 2 ⎞
Δμ = −⎜
⎜ 4m ⎟B
⎟ (7.9)
⎝ ⎠
Tampak bahwa momen induksi berlawanan arah dengan medan. Dengan kata lain,
respon elektron terhadap kehadiran medan adalah diamagnetik.


Dalam atom, orbit elektron berada dalam permukaan sferik. Tetapi, respon
diamagnetik efektif hanyalah pada penampang yang tegak lurus terhadap medan.
Dengan demikian, rata-rata r2 dalam ungkapan perubahan momen (7.9) di atas harus
diganti menjadi (2/3)r2, sehingga
⎛ e2r 2 ⎞
Δμ = −⎜
⎜ 6m ⎟B
⎟ (7.10)
⎝ ⎠
dengan r adalah radius bola. Apabila atom mempunyai Z elektron dan dalam satuan
volume terdapat N atom, maka suseptibilitas magnetik

χ=
M NZ Δμ
H
=
B / μo
μ e2
=− o
6m
NZ r 2( ) (7.11)

dengan r 2 adalah rata-rata kuadrat jari-jari elektron. Perata-rataan dilakukan atas
semua orbital elektron dalam atom. Tampak bahwa suseptibilitas tidak bergantung
pada suhu. Respon diamagnetik ini terjadi pada padatan yang sel atomiknya terisi
penuh. Seringkali digunakan ungkapan suseptibilitas molar yang didefinisikan
χmolar=NAχ/N.

7.3 GEJALA PARAMAGNET
Momentum angular orbital total suatu atom didefinisikan sebagai L = ∑ Li .
i

Sedangkan momentum angular spin totalnya S = ∑ S i . Pada keduanya, penjumlahan
i

dilakukan terhadap semua elektron, dan berharga tidak nol hanya untuk suatu sel
yang tidak penuh.
Momentum angular L dan S berinteraksi, sehingga menimbulkan
momentum angular total
J = L+S (7.12)
yang relatif konstan. Dengan demikian, L dan S berpresisi mengelilingi J , seperti



Gambar 7.2 Interaksi spin-orbit

⎛ e ⎞ ⎛e⎞
Momen dipol orbital μ L = −⎜ ⎟ L dan spin μ S = −⎜ ⎟ S , juga berpresisi di sekitar
⎝ 2m ⎠ ⎝m⎠

J . Momen dipol totalnya μ = μ L + μ S tidak segaris dengan J , dan juga berpresisi

di sekitar J dengan sudut θ. Karena frekuensi presisi yang cukup tinggi, maka yang

teramati hanyalah kompnen dari μ sepanjang J , yakni

⎛ e ⎞
μ rata − rata = μ cosθ = g ⎜ − ⎟J
⎝ 2m ⎠
dengan
j ( j + 1) + s ( s + 1) − l (l + 1)
g = 1+ (7.13)
2 j ( j + 1)
adalah faktor Lande.
Penentuan l, j dan s suatu atom memenuhi aturan Hund, yakti
(1). bilangan spin s cenderung mengambil harga maksimum dengan tetap berpegang
pada prinsip Pauli,
(2). demikian pula l, dan



(3). jika sel kurang dari separoh maksimum, maka j=|l-s|, dan jika sel sama atau lebih
dari separoh maksimum, maka j=l+s.
Dengan demikian, dapatlah dikatakan bahwa suatu atom yang selnya tidak penuh
mempunyai suatu momen magnetik permanen, yang terjadi dari kombinasi gerakan
orbital dan spin elektronnya.

Teori Klasik
Selanjutnya, untuk sederhananya, μ rata −rata disingkat μ saja. Energi potensial

dipol magnet dalam suatu medan magnet
V = −μ • B (7.14)
Dengan analisa yang sama dengan bahasan polarisasi listrik polar (subbab 6.3.2.1.1),
didapatkan momen dipol rata-rata dalam arah medan (misalnya, sumbu-Z)
μ 2B
μZ = (7.15)
3k oT
Magnetisasinya
μ 2B
M = N μZ = N (7.16)
3k o T
dan suseptibilitasnya
M μ μ2
χ= =N o (7.17)
H 3k oT

Tampak bahwa χ berbanding terbalik terhadap T. Hubungan ini disebut hukum Curie
dan suseptibilitasnya disebut suseptibilitas paramagnet Langevin.

Teori Kuantum
Saat medan magnet (misalnya, dalam arah sumbu-Z) dikenakan pada atom,
terjadilah “Zeeman splitting”
E = − μ • B = gμ B B m j (7.18)

e
dengan μ B = =9,3.10-24 Jm2/N disebut magneton Bohr.
2m



Misalnya, untuk j=1/2 dihasilkan tingkatan energi yang terpisah menjadi dua,
yang masing-masing bersesuaian dengan momen dipol paralel dan antiparalel dengan
arah medan, seperti ditunjukkan oleh Gambar 7.3 berikut.

mj=+1/2

ΔE=gμBB

mj=-1/2

Gambar 7.3 Zeeman splitting untuk j=1/2
Magnetisasinya
M = g μB (N1 –N2) (7.19)
Dengan g μB = komponen momen dalam arah-Z
N1 = konsentrasi atom di tingkat energi bawah
N2 = konsentrasi atom di tingkat energi atas
Perbandingan antara kedua konsentrasi memenuhi distribusi Boltzmann
N1
= e − ΔE / koT (7.20)
N2
dan hubungan N1+N2=N, dengan N adalah jumlah total konsentrasi. Oleh karena itu
magnetisasi (7.19) menjadi
e X − e−X
M = Ngμ B = Ngμ B tanh(x) (7.21)
e X + e−X
gμ B B
dengan x = . Sketsa M terhadap x ditunjukkan dalam Gambar 7.4 berikut.
k oT

M

NgμB

x

Gambar 7.4 Sketsa M terhadap x untuk sistem j=1/2



Tampak bahwa M sebanding dengan x untuk medan lemah dan M mencapai saturasi
saat medan listrik besar. Bila diambil kasus medan lemah, x<<1 dan tanh (x) ≅ x,
maka substitusi ke dalam (7.21) didapatkan suseptibilitas
μ o N ( gμ B ) 2
χ= (7.22)
k oT
Ungkapan ini sama dengan hasil teori klasik, tetapi dengan mengasumsikan momen
efektif atom μef=gμB√3.
Bentuk yang lebih umum, suatu atom dengan j tertentu akan mengalami
pembelahan tingkat energi sebanyak (2j+1) buah. Sedangkan suseptibilitasnya

μ o Nμ ef
2

χ= (7.23)
3k oT

dengan
μef = p μB dan p = g (j[j+1])1/2 (7.24)
Bilangan p disebut bilangan efektif magneton Bohr untuk suatu atom.
Eksperimen menunjukkan bahwa kristal ion tanah-jarang memenuhi hukum
Curie, dengan bilangan efektif magneton Bohr p seperti yang dijelaskan dalam teori
interaksi spin-orbit di atas. Dalam ion ini (La s/d Lu), sel 4f, yang menunjukkan
perilaku magnetik, terisi tidak penuh. Sel yang lebih luar, yaitu 5p terisi penuh, 5d
dan 6s berperan dalam pembentukan ion. Karena letaknya yang jauh lebih dalam,
maka elektron dalam sel 4f tidak dipengaruhi oleh ion lain dalam kristal. Perilaku
magnetiknya seperti ion bebas, sehingga momentum angular L dan S berkopel
sangat kuat.
Sedangkan untuk ion logam transisi, eksperimen menunjukkan bahwa j=s.
Dalam hal ini, sel terluar 3d terisi tidak penuh. Elektron dalam sel 3d ini berinteraksi
sangat kuat dengan ion tetangga, sehingga gerakan orbitalnya hanyut, dan tinggal
momen spin yang mengkontribusi terhadap proses magnetisasi. Gejala demikian
disebut “quenching”.

7.4 GEJALA MAGNETIK DALAM LOGAM


Kebanyakan logam bersifat paramagnet. Elektron konduksi dalam logam
mempunyai dua kontribusi, yaitu sifat paramagnet karena spinnya dan sifat
diamagnetik karena gerakan orbital yang diinduksikan oleh medan magnet.
Suseptibilitas elektronik nettonya adalah resultan dari kontribusi keduanya
χelektron = χspin + χorbital (7.25)

Paramagnetik Pauli
Apabila hanya memperhitungkan spin elektron saja, yakni j=s=1/2 dan g=2,
maka suseptibilitas bahan paramagnet (7.23) menjadi
μ o Nμ B
2
χ= (7.26)
k oT

Terlihat bahwa χ berbanding terbalik dengan T.
Tetapi, eksperimen menunjukkan bahwa suseptibilitas spin dalam logam,
pada pokoknya, tidak bergantung pada suhu. Disamping itu, nilai pengamatan
menunjukkan harga yang lebih kecil daripada ungkapan di atas. Perlu diketahui
bahwa elektron konduksi dalam logam bersifat delokalisasi dan mengikuti distribusi
Fermi-Dirac.
Sehubungan dengan paramagnetisme spin ini, perhatikanlah Gambar 7.5
berikut.

s=1/2
EFo

s=-1/2
B B

½g(E) ½g(E) 2μBB 2μBB

a b c

Gambar 7.5 Variasi tingkat energi karena pemakaian medan magnet
a. Distribusi elektron pada keadaan energi dimana medan nol
b. Perubahan tingkat energi saat medan baru dikenakan
c. Penyusunan kembali elektron ke dalam keadaan energi terendah saat
medan setimbang H



Ketika medan belum dikenakan, sebagian elektron berspin dalam arah-Z positip dan
sebagian lagi dalam arah-Z negatip sehingga resultan magnetisasi M=0. Tetapi, ketika
medan B dikenakan, tingkat energi spin yang paralel B mengalami penurunan sebesar
μBB; dan tingkat energi spin yang antiparalel B naik sebesar μBB. Kondisi yang tidak
stabil ini menyebabkan beberapa elektron dengan spin antiparalel B di dekat tingkat
Fermi berpindah ke spin paralel B sehingga magnetisasinya M≠0. Banyaknya
elektron yang sanggup berpindah (T=0 K) tersebut
E Fo + μ B B
1 1
Δn = ∫
E Fo
2
g ( E )dE ≅ g ( E Fo ) μ B B
2

Karena masing-masing spin mengalami perubahan sebesar 2μB (dari -μB ke +μB),
maka magnetisasi yang terjadi
M ≅ Δn 2 μ B = μ B g ( E Fo ) B
2

sehingga suseptibilitasnya
χ spin = μ o μ B g ( E F )
2
o
(7.27)

Tampak bahwa suseptibilitas bergantung pada rapat keadaan pada tingkat energi
Fermi; dan tidak bergantung pada suhu. Pengaruh suhu terhadap distribusi elektron
Fermi-Dirac memang kecil.
3 N
Mengingat bahwa harga g ( E Fo ) = (lihat persamaan (3.26) dan (3.30))
2 E Fo

untuk pita energi standard (E∼k2) dan EFo=koTF , maka suseptibilitas logam
3 T
χ spin ≅ χ (7.28)
2 TF

dengan χ adalah suseptibilitas klasik (Boltzmann) (7.26). Karena harga suhu Fermi
TF=30.000 K, maka harga χspin lebih kecil daripada χ dengan faktor pengecil 10-2,
yang sesuai pula dengan hasil eksperimen.
Pada logam transisi, suseptibilitas paramagnet besar sekali. Hal ini terjadi
karena g(EF) besar sebagai akibat sempit dan tingginya pita 3d.

Diamagnetik



Elektron konduksi dalam logam menunjukkan pula sifat diamagnetisme
karena gerakan siklotronnya di bawah pengaruh kehadiran medan magnet.
Pendekatan klasik menunjukkan kontribusi diamagnetisme total seluruh elektron
sama dengan nol. Tetapi, pendekatan kuantum menunjukkan bahwa kontribusi
suseptibilitas diamagnetik
1
χ orbital = χ spin (7.29)
3
Dengan demikian, suseptibilitas elektronik netto merupakan respon paramagnet.
Dalam membandingkan hasil teoritis dengan eksperimen, harus disertakan
efek diamagnetik ion “core” (diamagnetik Langevin). Misalnya, bila dalam
eksperimen diperoleh χtotal dan χcore, maka suseptibilitas elektronik konduksi logam
χelektron =χtotal - χcore

7.5 GEJALA FERROMAGNETIK
Gejala ferromagnetik adalah gejala terjadinya magnetisasi secara spontan
pada suatu bahan magnet. Ferromagnetik menyangkut pensejajaran sebagian besar
momen magnetik molekuler ke dalam suatu arah tertentu yang disukai dalam kristal.
Gejala ini terjadi pada elemen transisi dan tanah-jarang, yang mana sel 3d dan 4f
tidak terisi penuh. Contoh bahan ini adalah logam transisi, seperti Fe, Co dan Ni;
logam tanah-jarang, seperti Gd dan Dy; dan oksida logam transisi isolator CrO2.
Ferromagnetisme terjadi hanya di bawah suhu tertentu, yakni suhu Curie. Di
atas suhu Curie, momen berorientasi secara acak sehingga magnetisasinya nol dan
bahan menjadi paramagnet. Seperti halnya ferroelektrik, bahan ferromagnetik juga
menunjukkan adanya domain dan kurva histerisis.

7.5.1 Gejala Ferromagnetik pada Isolator
7.5.1.1 Teori Medan Molekuler
Antara momen yang berdekatan terjadi interaksi model Heisenberg, yang
bergantung pada spin, satu sama lain. Misalnya, interaksi antara atom i dan j, yang
masing-masing berspin si dan s j , menimbulkan energi pertukaran



Vex = − J ' s i • s j (7.30)

dengan J’ adalah konstanta pertukaran. Agar terjadi gejala ferromagnet, maka spin si
dan sj harus paralel, si = s j . Dengan demikian, agar energinya minimal, maka

konstanta J’ haruslah positip.
Jika diasumsikan bahwa interaksi pertukaran dipol hanya terjadi antartetangga
terdekat saja (konstanta J’ menurun tajam terhadap bertambahnya jarak antardipol),
maka energi pertukaran total dipol
Vex = - Z J’ s2
Dengan Z adalah jumlah tetangga terdekat dipol. Ekivalensi energi ini terhadap
medan magnet molekuler HW adalah melalui hubungan
Z J’ s2 = (g s μB) (μo HW) (7.31)
Dengan (gsμB) adalah momen dipol magnet. Dengan demikian, dapatlah dikatakan
bahwa interaksi pertukaran spin dipol dalam kristal terjadi karena adanya medan
molekuler; atau medan internal molekuler HW inilah yang menyebabkan terjadinya
magnetisasi spontan.
Weiss mengasumsikan bahwa medan internal sebanding dengan magnetisasi
HW = λ M (7.32)
dengan λ adalah konstanta Weiss. Nimal maksimum HW, yakni sama dengan
λM(0)=λNgsμB, terjadi pada T=0 K. Substitusi HW maksimum ke dalam (7.31)
menghasilkan
μ o N ( gμ B ) 2
J '= λ (7.33)
Z
Tampak bahwa J’ sebanding dengan λ dan masing-masing memiliki nilai 0,1 eV dan
104.

7.5.1.2 Magnetisasi Spontan dan Hukum Curie-Weiss
Magnetisasi spontan hanya disebabkan oleh adanya medan internal molekuler
HW. Bila diambil kasus untuk j=1/2, dengan analisa yang sama dengan bahasan gejala
paramagnet secara kuantum, maka dari persamaan (7.21) diperoleh magnetisasi



⎛ μ gμ λ M ⎞
M = N g μ B tanh ⎜ o B
⎜ ⎟
⎟ (7.34)
⎝ k oT ⎠
Solusi ungkapan ini dapat diselesaikan dengan metode grafik. Bila diambil
⎛ μ gμ λ M ⎞
tanh ⎜ o B
⎜ ⎟ = tanh ( x)
⎟
⎝ k oT ⎠
maka didapatkan dua ungkapan magnetisasi, yakni
k oT
M = x (7.35)
μ o gμ B λ
M = N g μ B tanh ( x ) (7.36)
Keduanya diplot bersamaan dalam grafik M terhadap x untuk mendapatkan titik
perpotongan sebagai solusinya, seperti ditunjukkan dalam Gambar 7.6 berikut.

M
T>TC
T=TC
M∼x

T<TC
M∼tanh(x)
A

x
Gambar 7.6 Kurva garis lurus M∼x dan M∼tanh(x) terhadap x.
Titik perpotongan A merepresentasikan magnetisasi spontan (keadaan ferromagnetik)

Suhu kritik (Curie) TC adalah suhu dimana garis lurus (grafik M∼x) merupakan
tangensial kurva hiperbolik pada titik asal. Tampak bahwa untuk T<TC, dua kurva
berpotongan di titik A, yang berarti bahwa magnetisasi spontan terjadi pada bahan
(karena adanya medan molekuler HW).
Pendekatan tanh(x)≅x, untuk x kecil, menjadikan kesamaan M dalam dua
persamaan (7.35) dan (7.36) menghasilkan ungkapan konstanta Weiss
k oTC
λ= (7.37)
μ o N ( gμ B )2
Bila harga TC=103 K dan N=1029m-3, maka didapatkan pendekatan harga λ≅104.



Dari grafik terlihat bahwa magnetisasi maksimum Ms(0)=NgμB terjadi jika
T→0 K. Dengan mengingat ungkapan konstanta Weiss (7.37), maka persamaan
(7.34) juga dapat ditulis dalam bentuk
M ⎛T ⎞
= tanh ⎜
⎜T ⎟
⎟ (7.38)
M ( 0) ⎝ C ⎠
yang secara grafik disajikan pada Gambar 7.7 berikut.

M/M(0)

1

0 T/TC
1

Gambar 7.7 Sketsa M(T)/M(0) terhadap T/TC untuk j=1/2
Grafik di atas adalah kurva universal untuk semua bahan magnet dengan nilai j=1/2.
Dalam daerah paramagnet, T>TC, medan total
Htotal = H + HW
Dengan H adalah medan eksternal yang dipasang. Bila diambil kasus untuk j=1/2
dalam medan total kecil, dengan analisa yang sama dengan bahasan gejala
paramagnet secara kuantum, maka dari persamaan (7.21) diperoleh
μ o gμ B
M = M ( 0) (H + λ M ) (7.39)
k oT

Dengan mengingat ungkapan λ dalam (7.37), maka diperoleh magnetisasi
C
M = H (7.40)
T − TC

TC μ o N ( gμ B ) 2
dengan C= = disebut konstanta Curie. Dengan demikian
λ k oT
suseptibilitas dalam daerah paramagnet



C
χ= (7.41)
T − TC
Ungkapan suseptibilitas ini sering disebut hukum Curie-Weiss.

7.5.2 Gejala Ferromagnetik pada Logam
Bahan ferromagnetik isolator tidak dapat digunakan secara langsung pada
logam. Misalnya, bilangan efektif magneton Bohr p untuk logam transisi adalah p=gs.
Tetapi, eksperimen menunjukkan bahwa bilangan tersebut adalah 2,22; 1,72 dan 0,54
masing-masing untuk Fe, Co dan Ni. Kegagalan ini terjadi karena bahasan
ferromagnetik isolator mengasumsikan bahwa elektron terlokalisasi di sekitar titik
kisi dan mengikuti distribusi Boltzmann. Sedangkan untuk elektron konduksi dalam
logam bersifat delokalisasi di seluruh ruang kristal dan mengikuti distribusi Fermi-
Dirac.
Bahasan ferromagnetik dalam menggunakan model elektron-itinerant yang
dikembangkan oleh Stoner. Perhatikanlah Gambar 7.8 berikut.

Bω=μoHω

a b

Gambar 7.8 Proses magnetisasi dalam model itinerant
Pita dibagi menjadi dua subpita, masing-masing dengan orientasi spin “up’ dan
“down”. Keadaan nonmagnetik (Gambar 7.8.a) ditandai oleh populasi sama dalam
dua subpita sehingga resultan magnetisasi nol.
Karena interaksi pertukaran, momen berusaha dalam arah “up” (energi yang
lebih rendah). Untuk itu, elektron harus berpindah dari daerah “down” ke “up”; dan
hal ini menimbulkan magnetisasi. Akibatnya, energi kedua subpita tidak sama lagi.
Kedua pita mengalami perpindahan relatif satu sama lain (Gambar 7.8.b). Dengan



demikian, magnetisasi bergantung pada perpindahan relatif subpita (atau interaksi
pertukaran) dan bentuk pita.
Energi pertukaran yang hilang dari sebuah elektron yang berpindah dari arah
“down” (-μB) ke “up” (+μB)
1
2 BW M = 1
2
(μ o H W )M = 1 μ o λ M 2 = 2μ o λ μ B
2
2

karena M=2μB. Ternyata, tidak semua elektron dalam arah “down” dapat berpindah,
melainkan hanya elektron yang berada di dekat energi Fermi EF. Misalnya, ΔE
merupakan rentang energi dalam subpita “up” yang hendak ditempati elektron yang
berpindah, maka jumlah elektron yang berpindah tersebut

n = 1 g ( E Fo ) ΔE
2

dengan g(EFo) adalah rapat keadaan pada tingkat Fermi. Jika n=1, maka diperoleh

2
ΔE =
g ( E Fo )

Dengan demikian, syarat agar terjadi gejala ferromagnetik adalah

2
2μ o λ μ B >
2
(7.42))
g ( E Fo )

Untuk memenuhi syarat tersebut, maka konstanta pertukaran harus besar, yakni jika
sel atomik beradius kecil. Juga, g(EFo) harus besar, yang berarti menuntut pita sempit.
Sel beradius lebih kecil mempunyai kemungkinan overlap fungsi gelombang
lebih kecil dan karenanya pita menjadi lebih sempit. Hal ini dipenuhi oleh pita 3d
dalam Fe, Co dan Ni; dan pita 4f dalam Gd dan Dy. Nilai g(EFo) besar menyebabkan
pita dapat menampung elektron lebih banyak dalam rentang energi kecil. Tetapi,
g(EFo) kecil menyebabkan pita melebar, seperti pita 4s, yang tidak menunjukkan
gejala ferromagnetik.

7.6 GEJALA ANTIFERROMAGNETIK DAN FERRIMAGNETIK



Berkaitan dengan keteraturan magnetik pada bahan, maka perhatikanlah
Gambar 7.9 berikut.

a b c

Gambar 7.9 Susunan magnetik
a. ferromagnetik, b. antiferromagnetik, dan c. ferrimagnetik

Ferromagnetik
Semua dipol disejajarkan dalam arah yang sama sehingga bahan berada dalam
keadaan termagnetisasi penuh.

Antiferromagnetik
Masing-masing dipol mempunyai momen yang sama. Tetapi dipol yang
berdekatan berlawanan arahnya. Dengan demikian, masing-masing dipol saling
meniadakan satu sama lain, sehingga magnetisasi netto sama dengan nol. Gejala ini
banyak ditunjukkan oleh senyawa logam transisi, seperti kristal MnF2.

Ferrimagnetik
Dipol yang berdekatan berlawanan arah. Tetapi karena masing-masing
momen tidak sama, maka terdapat magnetisasi netto yang tidak sama dengan nol.
Bahan ferrimagnetik sering disebut ferrit, yakni kristal oksida ionik Xfe2O4, dimana
X adalah logam divalen. Contoh ferrit adalah magnetit (“lodestone”) Fe3O4.

RINGKASAN
01. Pada bahan yang ditempatkan dalam medan magnet luar yang berintensitas H ,
terjadi magnetisasi M , dan juga, terjadi induksi magnet B . M dan H
direlasikan oleh suseptibilitas magnetik χ; sedangkan B dan H direlasikan oleh
permeabilitas bahan μ. Berdasarkan tanda dan besar nilai suseptibilitas magnet
suatu bahan dikelompokkan menjadi (a). paramagnet, (b). diamagnet, dan (c).
ferromagnet.



02. Elektron yang beredar mengelilingi inti atom dalam medan magnet B mengalami
gejala diamagnetik Langevin, yakni momen induksi berlawanan arah dengan
medan. Respon diamagnetik ini terjadi pada padatan yang sel atomiknya terisi
penuh.
03. Momentum angular orbital dan spin total suatu atom, masing-masing adalah L
dan S berinteraksi membentuk momentum angular total J, sehingga L dan S
berpresisi mengelilingi J. L dan S berharga tidak nol hanya untuk suatu sel yang
tidak penuh. Demikian pula, momen dipol orbital μL dan spin μS berpresisi
terhadap J, tetapi momen dipol totalnya μ = μ L + μ S tidak segaris dengan J .

Karena itu dicari momen dipol total rata-rata sepanjang J, yaitu
⎛ e ⎞ j ( j + 1) + s ( s + 1) − l (l + 1)
μ rata − rata = μ cosθ = g ⎜ − ⎟ J dengan g = 1 + adalah
⎝ 2m ⎠ 2 j ( j + 1)
faktor Lande.
04. Hasil bahasan teori klasik adalah bahwa suseptibilitas paramagnet Langevin χ
berbanding terbalik terhadap T. Sedangkan teori kuantum memperoleh
μ o Nμ ef
2

suseptibilitas χ = dengan μef = p μB dan p = g (j[j+1])1/2. Bila gerakan
3k oT

orbitalnya hanyut, dan tinggal momen spin yang mengkontribusi terhadap proses
magnetisasi, maka disebut “quenching”.
05. Elektron konduksi dalam logam mempunyai dua kontribusi, yaitu sifat
paramagnet karena spinnya dan sifat diamagnetik karena gerakan orbital yang
diinduksikan oleh medan magnet. Oleh karaean itu gejala magnetik dalam logam
meliputi dua hal, yaitu Paramagnetik Pauli dan diamagnetik. Bahasan
Paramagnetik Pauli memperoleh suseptibilitas χ spin = μ o μ B g ( E F ) , yang
2
o

bergantung pada rapat keadaan pada tingkat energi Fermi; dan tidak bergantung
pada suhu. Sedangkan bahasan diamagnetik, melalui pendekatan kuantum
1
menunjukkan bahwa kontribusi suseptibilitas diamagnetik χ orbital = χ spin
3
sehingga suseptibilitas elektronik netto merupakan respon paramagnet.


06. Gejala ferromagnetik adalah gejala terjadinya magnetisasi secara spontan pada
suatu bahan magnet dan terjadi hanya di bawah suhu tertentu, yakni suhu Curie.
Bahan ferromagnetik juga menunjukkan adanya domain dan kurva histerisis.
Bahasan gejala ferromagnetik meliputi dua hal, yaitu pada isolator dan logam.
07. Gejala ferromagnetik dalam isolator memakai teori medan molekuler. Teori ini
C
menghasilkan suseptibilitas dalam daerah paramagnet χ = , yang sering
T − TC
disebut hukum Curie-Weiss.
08. Gejala ferromagnetik dalam logam menasumsikan bahwa elektron konduksi
dalam logam bersifat delokalisasi di seluruh ruang kristal dan mengikuti distribusi
Fermi-Dirac. Bahasan ini menggunakan model elektron-itinerant yang
dikembangkan oleh Stoner. Model ini memiliki syarat agar terjadi gejala
2
ferromagnetik, yaitu 2μ o λ μ B >
2
. Berarti sel atomik harus beradius kecil.
g ( E Fo )
Juga, g(EFo) harus besar, yang berarti menuntut pita sempit.

09. Berkaitan dengan keteraturan magnetik pada bahan, maka terdapat (a)
ferromagnetik, (b) antiferromagnetik, dan (c) ferrimagnetik.

LATIHAN SOAL BAB VII

01. Sebuah elektron yang bergerak melingkar beraturan mempunyai momen dipol
magnetik μ seperti persamaan (7.6). Jika momentum angular elektron tersebut
adalah L, maka buktikan bahwa
e
μ=− L
2m
02. Pada suhu 4 K padatan Argon mempunyai konsentrasi 2,66.1028 atom/m3. Jika
jarak kuadrat rata-rata sebuah elektron terhadap inti terdekat 0,62 Å, maka
a. hitunglah suseptibilitasnya!



b. hitunglah magnetisasinya dalam medan induksi 2,0 T!
03. Hitunglah faktor Lande g untuk keadaan dasar
a. ion Praseodymium 59Pr yang mempunyai 2 elektron pada subkulit f!
b. ion Erbium 68Er yang mempunyai 11 elektron pada subkulit f!

04. Nikel mempunyai 8 elektron dalam sel 3d.
a. Hitunglah bilangan efektif magneton Bohr ion Nikel bila
(1). Momentum angular orbital tidak “quenching”!
(2). Terjadi “quenching”!
b. Nilai eksperimen menunjukkan bahwa harga p=3,2. Apa komentar Anda?
05. Kontribusi teras (“core”) diamagnetik natrium terhadap suseptibilitas molar
adalah sebesar -6,1.10-12 m3/mol.
a. Hitunglah jarak rata-rata elektron teras terhadap inti terdekat!
b. hitunglah momen dipol teras dalam medan magnet induksi 0,5 T!
06. Dengan menggunakan aturan Hund, hitunglah bilangan kuantum l, s, j, faktor
Lande g dan momen dipol magnet untuk ion Vanadium 23V dengan 3 elektron
dalam sel 3d, bila dianggap momentum angular orbital
a. tidak mengalami “quenching”!
b. mengalami “quenching”!
07. Dengan menggunakan aturan Hund, hitunglah faktor Lande
a. untuk setiap bilangan yang mengisi sel d (1 s/d 10)! Anggaplah bahwa atom
berada dalam keadaan dasar dan momentum angular orbital tidak
“quenching”.
b. untuk bilangan berapakah momen dipol magnetnya nol? Atom apakah itu?
c. untuk bilangan berapakah momen dipol magnetnya terbesar? Atom apakah itu?
d. Ulangi soal (b) dan (c) bila momentum angular orbital mengalami
“quenching”.
08. Ion magnetik paramagnetik dalam pengaruh medan magnet akan memperoleh
energi seperti persamaan (7.18). Bila bahan paramagnet tersebut mempunyai



momentum angular total ђ, faktor Lande g=2 dan medan magnet induksi 0,7 T
serta memenuhi distribusi Maxwell-Boltzmann, maka
a. hitunglah fraksi atom dengan JZ=+ђ, dengan JZ=0 dan dengan JZ=-ђ pada suhu
300 K!
b. hitunglah momen dipol atomik rata-rata!
09. Pada suhu kamar Oksigen merupakan gas paramagnetik dengan suseptibilitas
molar 4,33.10-8 m3/mol.
a. Hitunglah bilangan efektif magneton Bohr peratom!
b. Tunjukkan bahwa soal (a) sesuai dengan sel s dengan 2 elektron!
10. Dua bahan ferromagnetik mempunyai struktur kristal dan ukuran sel satuan yang
identik. Spin atomnya identik, tetapi koefisien pertukaran J’ yang satu berharga
dua kali yang lain. Bandingkan konstanta Weiss λ, konstanta Cuire C,
magnetisasi saturasi M(0) dan suhu Cuire TC antara keduanya!
11. Suseptibilitas diamagnetik karena ion teras (“cores”) dalam logam Tembaga
adalah -0,2.10-6. Jika diketahui bahwa kerapatan Cu adalah 8,93 gr/cm3 dan berat
atomnya 63,5 gr/mol, maka hitunglah jari-jari rata-rata ion tersebut!
12. Germanium mempunyai kerapatan 5,38 gr/cm3 dan berat atom 72,6 gr/mol.
a. Jika diketahui bahwa suseptibilitasnya -0,8.10-5 dan radius ion teras (“core”)
0,44 Å, maka hitunglah persentase dari kontribusi ikatan kovalen terhadap
suseptibilitasnya!
b. Jika dikenakan medan H=5.104 A/m, maka hitunglah magnetisasi dan induksi
magnetnya!
13. Suatu sistem dengan spin j=s=1/2 ditempatkan dalam suatu medan magnet
H=5.104 A/m,. Hitunglah
a. fraksi ion yang paralel terhadap medan pada suhu kamar!
b. komponen rata-rata momen dipol searah medan pada suhu kamar!
c. medan untuk u Z =0,5μB!
d. Ulangi soal (a) dan (b) pada suhu sangat rendah 1 K!
14. Turunkanlah persamaan (7.23)!



15. Buktikanlah bahwa momen dipol rata-rata auatu atom, yang mengandung efek
interaksi spin-orbit, mempunyai ungkapan
⎛ e ⎞
u rata − rata = g ⎜ − ⎟J
⎝ 2m ⎠
dengan g adalah faktor Lande (7.13)!
16. a. Suseptibilitas spin elektron konduksi pada T=0 K diberikan oleh persamaan
(7.27). Nyatakalah hasil ini dalam bentuk konsentrasi elektron untuk pita energi
standard!
b. Hitunglah suseptibilitas spin logam K, bila diketahui kerapatan 0,87 gr/cm3
dan berat atom 39,1 gr/mol!
c. Hitunglah suseptibilitas diamagnetik elektron konduksi logam K!
d. Hitung jari-jari rata-rata ion K dalam keadaan logam!
17. Data untuk Fe: magnetisasi saturasi M(0)=1,74.106 A/m, suhu Fermi TF=1043 K,
kerapatan ρm=7,92 gr/cm3 dan berat atom M=55,6 gr/mol.
a. Buktikanlah bahwa momen dipol sebuah atom Fe adalah 2,22 μB!
b. Hitunglah konstanta pertukaran Weiss λ dan medan molekuler HW!
c. hitunglah konstanta Curie!
d. Hitunglah energi pertukaran untuk suatu interaksi dipol antartetangga terdekat!


DAFTAR RUJUKAN
Alonso, M., Finn, EJ. 1972. Fundamental University Physics III: Quantum and
Statistical Physics. California: Addison Wesley Publishing Company

Ashcroft, NW,. Mermin, ND. 1976. Solid State Physics. Philadelphia: Sounders
College

Chrisman, FR. 1984. Fundamental of Solid State Physics. Singapura: John Wiley
& Sons, Inc

Kittel, C. 1991. Introduction to Solid State Physics. Singapura: John Wiley &
Sons, Inc

Omar, MA. 1975. Elementary Solid State Physics. Reading-Massachusetts:
Addison Wesley Publishing Company

Pointon, AJ. 1976. An Introduction to Statistical Physics for Student. London:
Longman

Supangkat, H. Diktat Matakuliah Susunan Zat. Bandung: Jurusan Fisika FMIPA
ITB

Suwitra, N. 1989. Pengantar Fisika Zat Padat. Jakarta: Depdikbud Dirjendikti
P2LPTK

Zat padat parno

More Related Content

What's hot

Similar to Zat padat parno

Zat padat parno