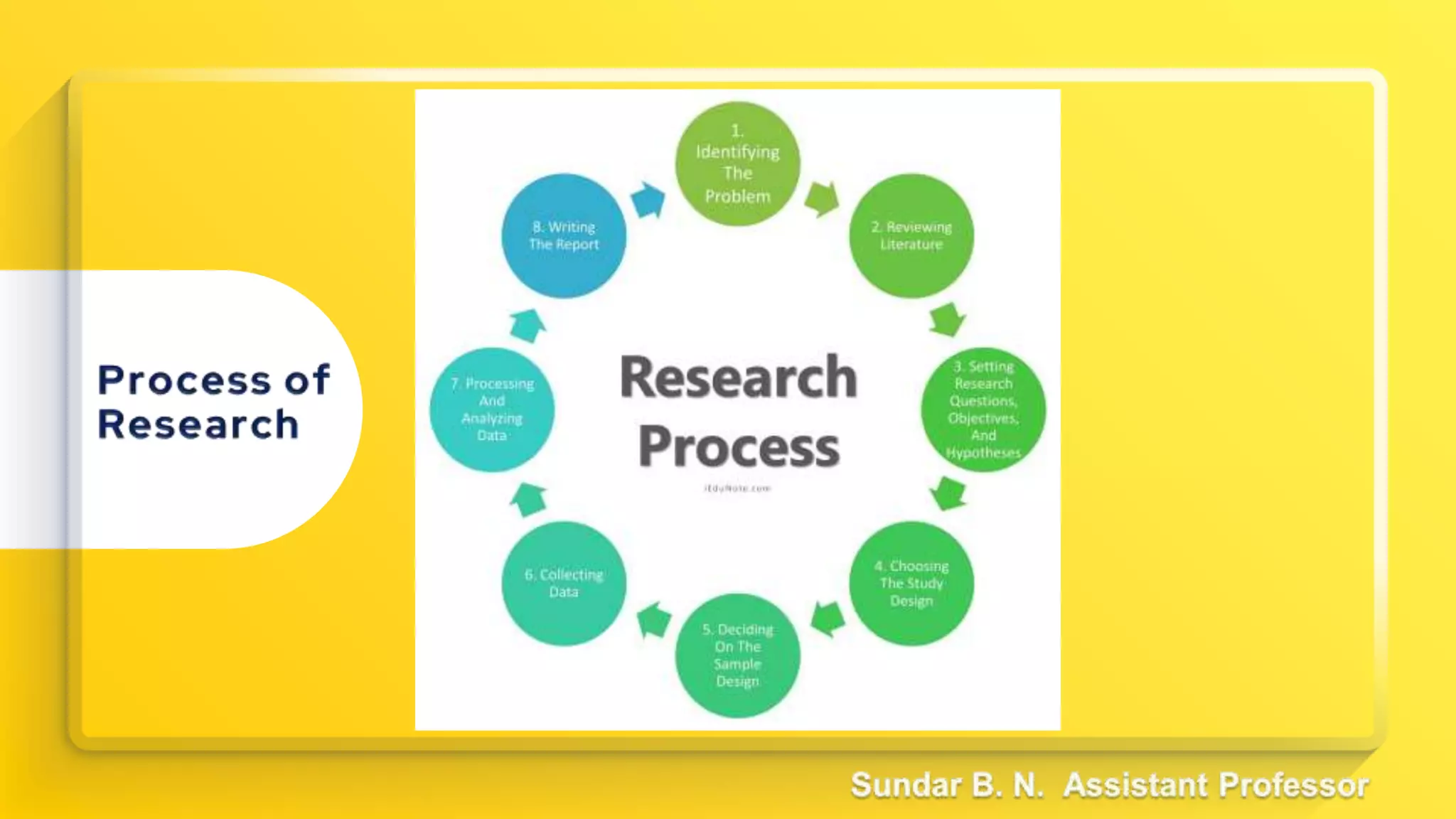
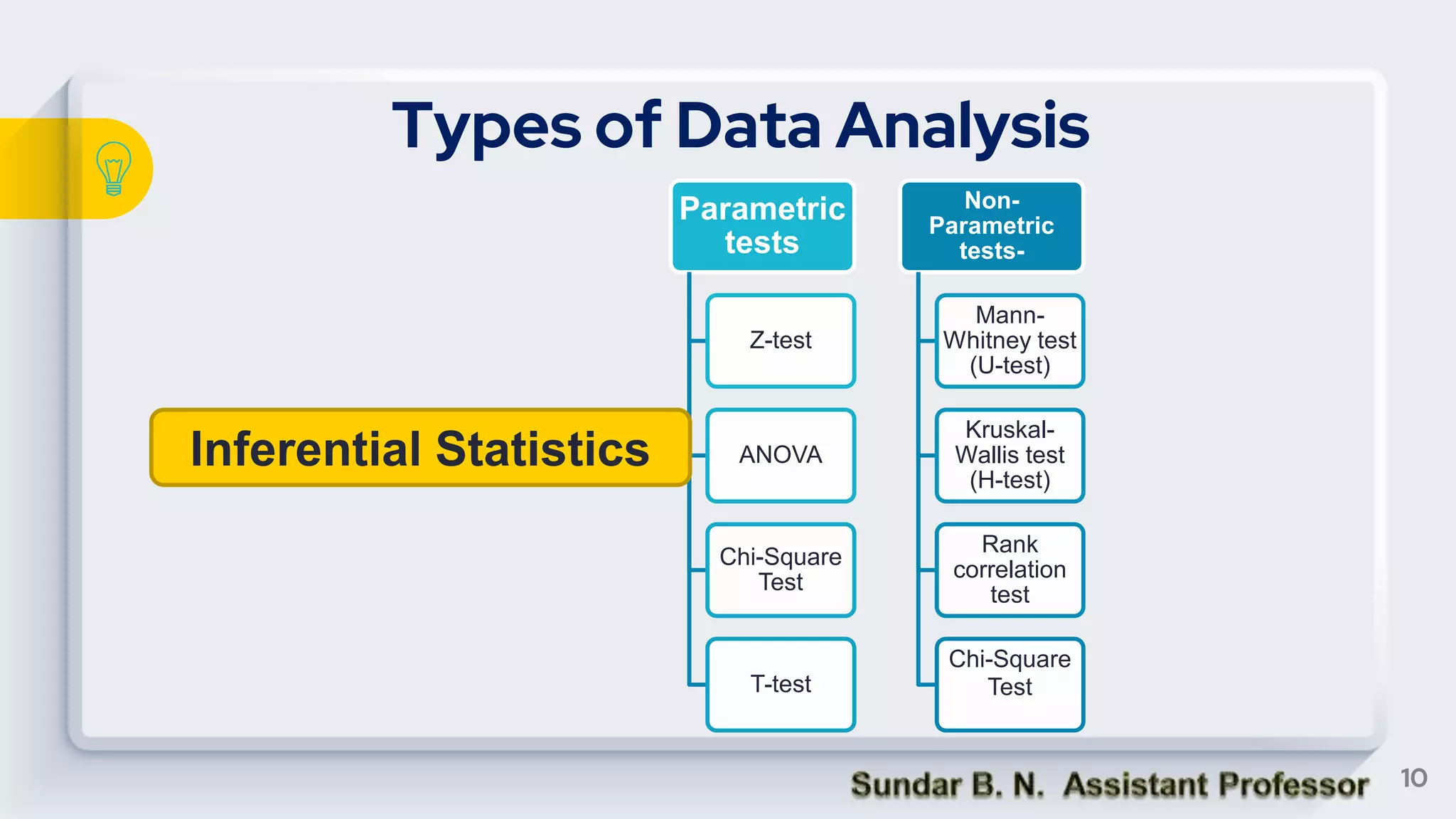
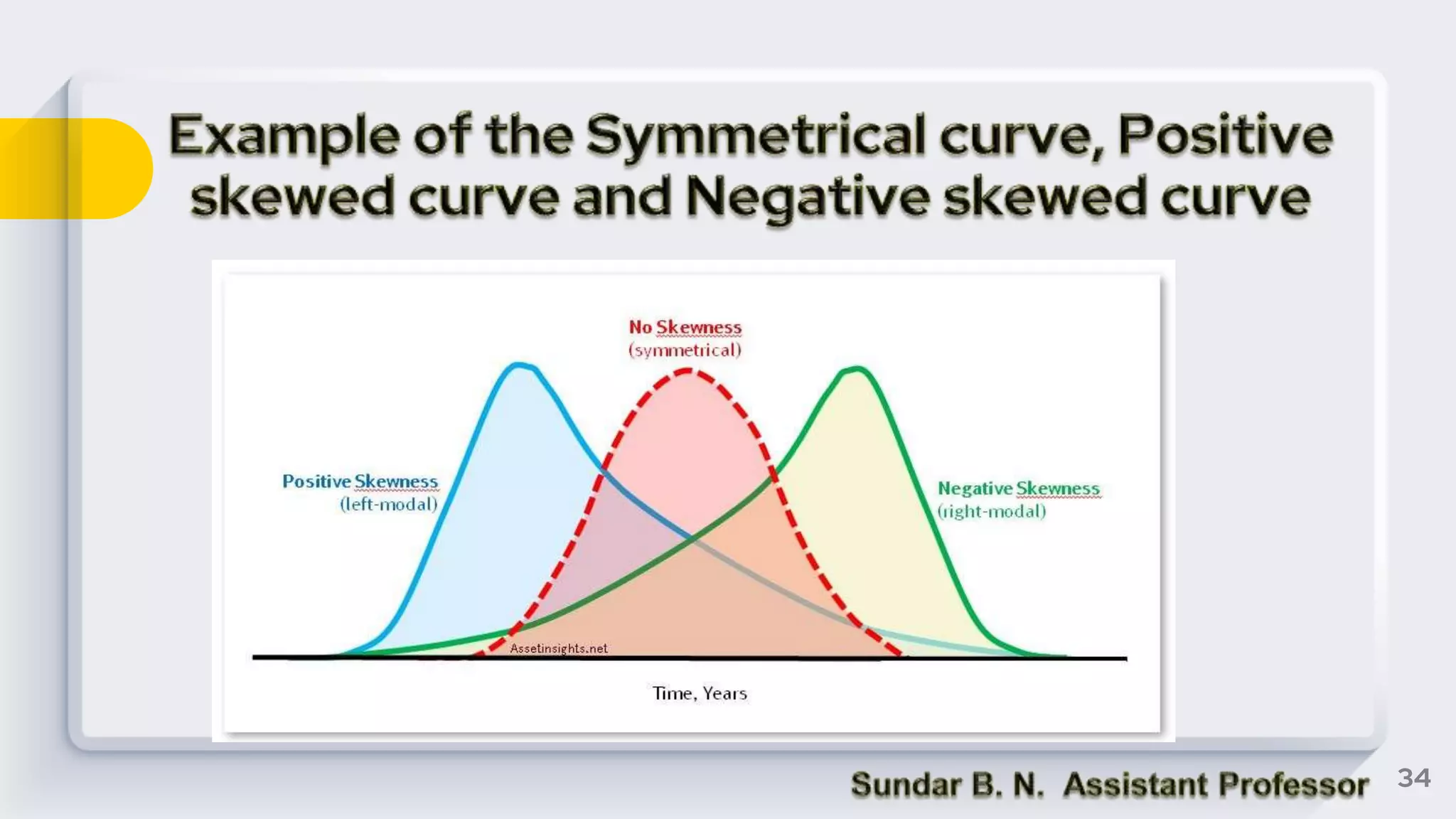
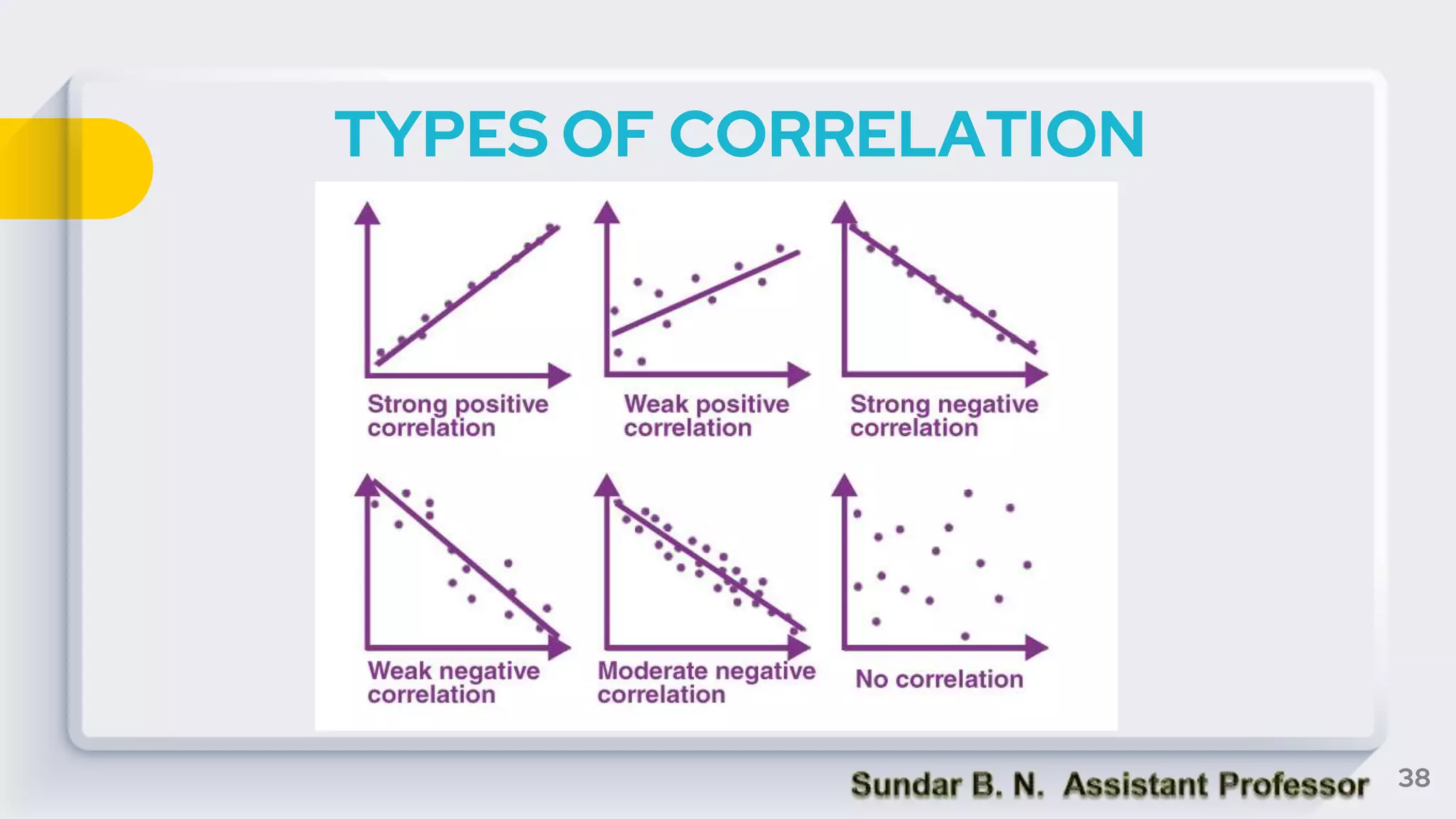
The document provides an overview of key statistical concepts including measures of central tendency, measures of dispersion, data analysis techniques, and the differences between correlation and regression. It details various types of data, methods for analyzing data, and their significance in interpreting statistical findings. Additionally, it describes different statistical measures such as mean, median, mode, variance, and standard deviation, as well as concepts like skewness and its impact on data interpretation.

2. 2
Measures of Central Tendency
Measures of Position
Measures of Dispersion
Skewness
Correlation
Regression Analysis

3. Meaning of Research
Research is an investigative process of finding reliable solution to a
problem through a systematic selection, collection, analysis and
interpretation of data relating to problem.
3

5. Data analysis is the process of systematically
applying statistical and logical techniques to
describe, illustrate, condense and recap and
evaluate data
Technically speaking, processing implies editing,
coding, classification and tabulation of collected
data so that they are amenable to analysis.
5

6. DATA
Data play the role of raw material for any statistical
investigation and defined in a single sentence as
“The values of different objects collected in a survey or
recorded values of an experiment over a time period taken
together constitute what we call data in Statistics”
Each value in the data is known as observation.
6

7. DEFINITION OF STATISTICS
“Statistics are the numerical statements of facts in any department of
enquiry placed in relation to each other.” – A.L. Bowly.
“The science which deals with the collection, tabulation, analysis and
interpretation of numerical data.” – Croxton and Cowden.
“Statistics is a branch of science which deals with collection,
classification, tabulation, analysis and interpretation of data.”
7

8. Types of Data Analysis
 Descriptive Statistics - provide an overview of the attributes
of a data set. These include measurements of central tendency
(frequency, histograms, mean, median, & mode) and dispersion
(range, variance & standard deviation)
 Inferential Statistics - provide measures of how well your
data support your hypothesis and if your data are generalizable
beyond what was tested (significance tests).
These include hypothesis testing and estimates.
8

9. Types of Data Analysis
Descriptive
Statistics
9

10. Types of Data Analysis
10
Parametric
tests
Z-test
ANOVA
Chi-Square
Test
T-test
Non-
Parametric
tests-
Mann-
Whitney test
(U-test)
Kruskal-
Wallis test
(H-test)
Rank
correlation
test
Chi-Square
Test
Inferential Statistics

11. Measures of Central Tendency
● According to Professor Bowley, averages are “statistical constants
which enable us to comprehend in a single effort the
significance of the whole”.
● Measures of central tendency show the tendency of some central
value around which data tend to cluster.
11

12. Arithmetic Mean
Weighted Mean
Geometric Mean
Harmonic Mean
Median
Mode
12

13. Arithmetic mean (also called mean) is
defined as the sum of all the observations
divided by the number of observations.
It is particularly useful when we are
dealing with a sample as it is least
affected by sampling fluctuations.
It is the most popular average and should
always be our first choice unless there is a
strong reason for not using it.
13

14. WEIGHTED MEAN
A weighted mean is a kind of average .
Instead of each data point contributing
equally to the final mean, some data
points contribute more “weight” than
others.
If all the weights are equal, then the
weighted mean equals the arithmetic
mean.
Weighted means are very common in
statistics, especially when
studying populations.
14

15. Geometric Mean
15

16. Harmonic Mean
HM is defined as the value
obtained when the number of
values in the data set is divided by
the sum of reciprocals.
The harmonic mean (HM) is
defined as the reciprocal (inverse)
of the arithmetic mean of the
reciprocals of the observations of
a set.
16

17. MEDIAN
Median is that value of the variable which
divides the whole distribution into two
equal parts.
The data should be arranged in
ascending or descending order of
magnitude.
When the number of observations is odd
then the median is the middle value of
the data.
For even number of observations, there
will be two middle values.
17

18. MODE
Highest frequent observation in the
distribution is known as mode.
In other words, mode is that
observation in a distribution which has
the maximum frequency.
For example, when we say that the
average size of shoes sold in a shop is 7
it is the modal size which is sold most
frequently.
18

19. Relationship between Mean, Median
and Mode
For a symmetrical distribution
the mean, median and mode
coincide.
But if the distribution is
moderately asymmetrical, there
is an empirical relationship
between them.
19

20. 20

21. PARTITION VALUES
Partition values are those values of
variable which divide the
distribution into a certain
number of equal parts.
Here it may be noted that the data
should be arranged in ascending or
descending order of magnitude.
21

22. Deciles divide whole distribution in
to ten equal parts.
There are nine deciles.
D1, D2,...,D9 are known as 1st Decile,
2nd Decile,...,9th Decile
respectively and ith Decile contains
the (iN/10)th part of data.
Here, it may be noted that the data
should be arranged in ascending or
descending order of magnitude.
22

23. PERCENTILE
Percentiles divide whole distribution
in to 100 equal parts.
There are ninety nine percentiles.
P1, P2, …,P99 are known as 1st
percentile, 2nd percentile,…,99th
percentile and ith percentile contains
the (iN/100)th part of data.
Here, it may be noted that the data
should be arranged in ascending or
descending order of magnitude.
23

24. QUARTILES
Quartiles divide whole distribution in to four
equal parts.
There are three quartiles- 1st Quartile
denoted as Q1, 2nd Quartile denoted as Q2
and 3rd Quartile as Q3, which divide the
whole data in four parts.
1st Quartile contains the ¼ part of data, 2nd
Quartile contains ½ of the data and 3rd
Quartile contains the ¾ part of data.
Here, it may be noted that the data should be
arranged in ascending or descending order of
magnitude.
24

25. 25
Measure of dispersion is
calculated to get an idea
about the variability in
the data.
According to Spiegel, the
degree to which
numerical data tend to
spread about an average
value is called the
variation or dispersion of
data.

26. 26
Actually, there are two basic kinds of a measure of
dispersion
(i) Absolute measures - used to measure the
variability of a given data expressed in the same unit.
(ii) Relative measures - used to compare the
variability of two or more sets of observations

27. 27
MEASURES OF
DISPERSION
Absolute
measures
Range
Quartile
Deviation
Mean
Deviation
Standard
Deviation
Variance
Relative
measures
Coefficient
of Range
Coefficient
of Quartile
Deviation
Coefficient
of Mean
deviation
Coefficient
of
variation

28. Range
Range is the simplest measure of dispersion.
It is defined as the difference between the
maximum value of the variable and the
minimum value of the variable in the
distribution.
Its merit lies in its simplicity.
The demerit is that it is a crude measure
because it is using only the maximum and the
minimum observations of variable.
R=X max-X min
where, X max : Maximum value of variable and
X min : Minimum value of variable
28

29. Quartile Deviation
Quartile deviation is a statistic that
measures the deviation in the
middle of the data.
Quartile deviation is also referred
to as the semi interquartile
range and is half of the difference
between the third quartile and
the first quartile value.
29

30. Mean Deviation
Mean deviation is defined as
average deviation from any
arbitrary value viz. mean, median,
mode, etc.
It is often suggested to calculate it
from the median because it gives
least value when measured from the
median.
30

31. VARIANCE
While calculating the mean deviation,
negative deviations are straightaway
made positive.
To overcome this drawback we move
towards the next measure of dispersion
called variance.
Variance is the average of the square of
deviations of the values taken from mean.
Taking a square of the deviation is a
better technique to get rid of negative
deviations.
31

32. Standard Deviation
The standard deviation of a
random variable, sample, statistical
population, data set, or probability
distribution is the square root of
its variance.
A low SD and high SD
32

33. SKEWNESS
In addition to measures of central
tendency and dispersion,
we also need to have an idea about the
shape of the distribution.
Measure of Skewness gives the
direction and the magnitude of the
lack of symmetry.
Skewness means lack of symmetry.
In Statistics, a distribution is called
symmetric if mean, median and mode
coincide.
33

34. 34

35. VARIOUS MEASURES OF SKEWNESS
Measures of skewness help us to know to what degree and in which
direction (positive or negative) the frequency distribution has a departure
from symmetry.
Although positive or negative skewness can be detected graphically
depending on whether the right tail or the left tail is longer but, we don’t
get idea of the magnitude.
Besides, borderline cases between symmetry and asymmetry may be
difficult to detect graphically.
Hence some statistical measures are required to find the magnitude of lack
of symmetry.
35

36. VARIOUS MEASURES OF SKEWNESS
Absolute Measures of Skewness
Following are the absolute measures of
skewness:
1. Skewness (Sk) = Mean – Median
2. Skewness (Sk) = Mean – Mode
3. Skewness (Sk) = (Q3-Q2)-(Q2-Q1)
Relative Measures of Skewness
 Karl Pearson’s coefficient of
skewness=
Sk=Mean-Mode/SD
Sk(P)=3(Mean-Mode)/SD
 Bowley’s coefficient of skewness
Sk(B)=Q3+Q1-2Md/Q3-Q1
36

37. CORRELATION
Correlation was developed in 1885
by Francis Galton
Observations are available on two or more
variables.
When two variables are related in such a
way that change in the value of one
variable affects the value of another
variable, then variables are said to be
correlated or there is correlation
between these two variables.
Examples
1. Heights and weights of persons of
a certain group;
2. Sales revenue and advertising
expenditure in business; and
3. Time spent on study and marks
obtained by students in exam.

38. TYPES OF CORRELATION
38

39. COEFFICIENT OF CORRELATION
Scatter diagram tells us whether variables are
correlated or not.
But it does not indicate the extent of which they
are correlated.
If X and Y are two random variables then
correlation coefficient between X and Y is
denoted by r and defined as
Coefficient of correlation measures the intensity
or degree of linear relationship between two
variables.
It was given by British Biometrician Karl
Pearson (1867-1936).
39
Coefficient of correlation gives the
exact idea of the extent of which
they are correlated.

40. LINEAR REGRESSION
If two variables are correlated significantly, then
it is possible to predict or estimate the values of
one variable from the other.
Regression analysis is a statistical technique which is
used to investigate the relationship between
variables.
40
Examples for Simple Regression
 The effect of price increase on
demand
 The effect of change in the money
supply on the increase rate
 Effect of change in expenditure on
advertisement on sales and profit in
business are such examples
where investigators or researchers try to
construct cause and affect relationship.

41. The concept of Regression Analysis
developed by Sir Fransis Galton (1822-
1911) in his article “Regression towards
mediocrity in hereditary structure”
The term, regression, was originally
used in 1885 by Sir Francis Galton in his
analysis of the relationship between the
heights of children and parents.
41
Who
developed
Regression
Analysis

42. DISTINCTION BETWEEN CORRELATION
AND REGRESSION
(i) Correlation studies the linear relationship between two variables while
regression analysis is a mathematical measure of the average relationship
between two or more variables.
(ii) Correlation has limited application because it gives the strength of linear
relationship while the purpose of regression is to "predict" the value of the
dependent variable for the given values of one or more independent variables.
(iii) Correlation makes no distinction between independent and dependent variables
while linear regression does it, i.e. correlation does not consider the concept of
dependent and independent variables while in regression analysis one variable is
considered as dependent variable and other(s) is/are as independent variable(s).
42