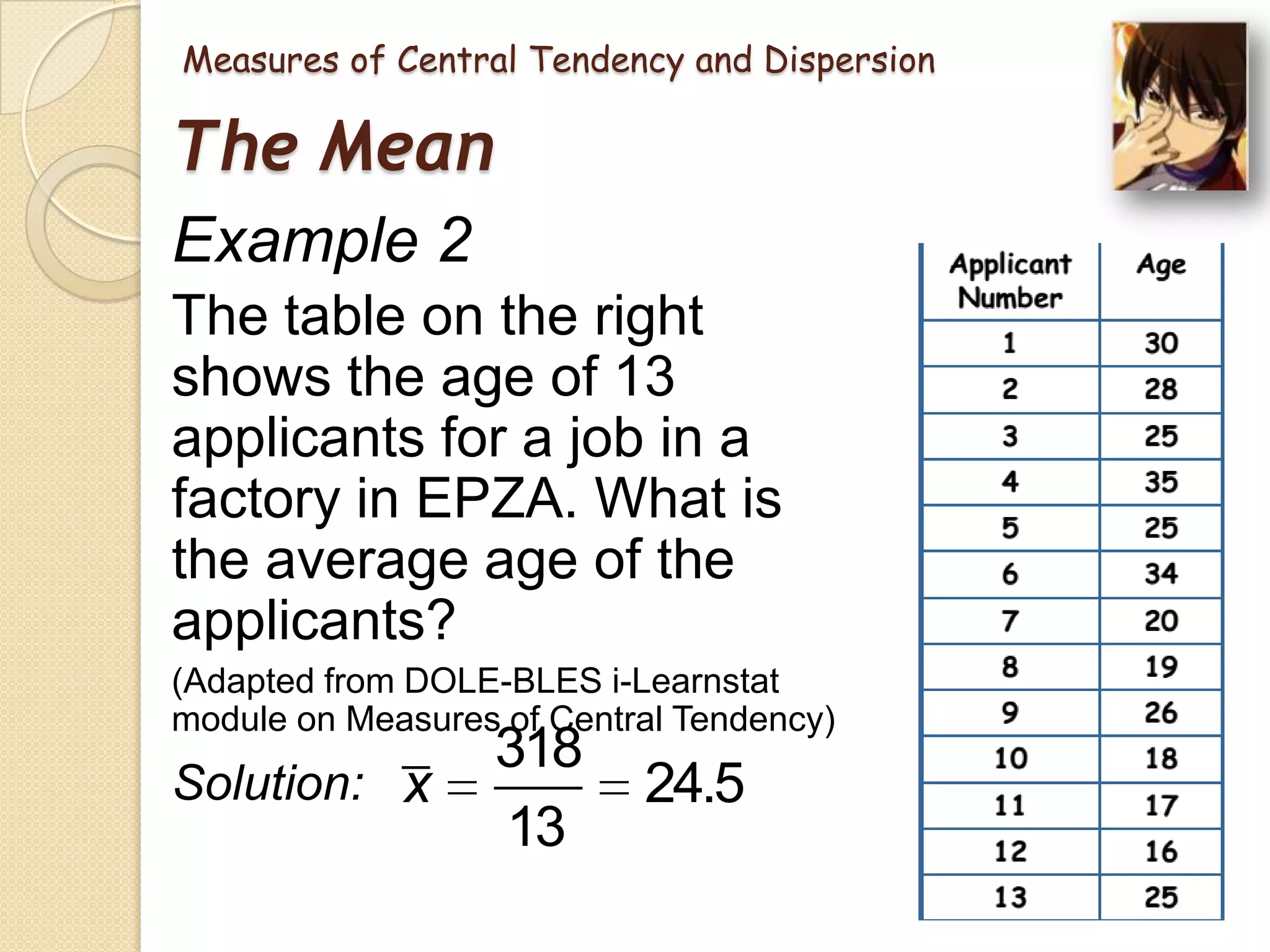
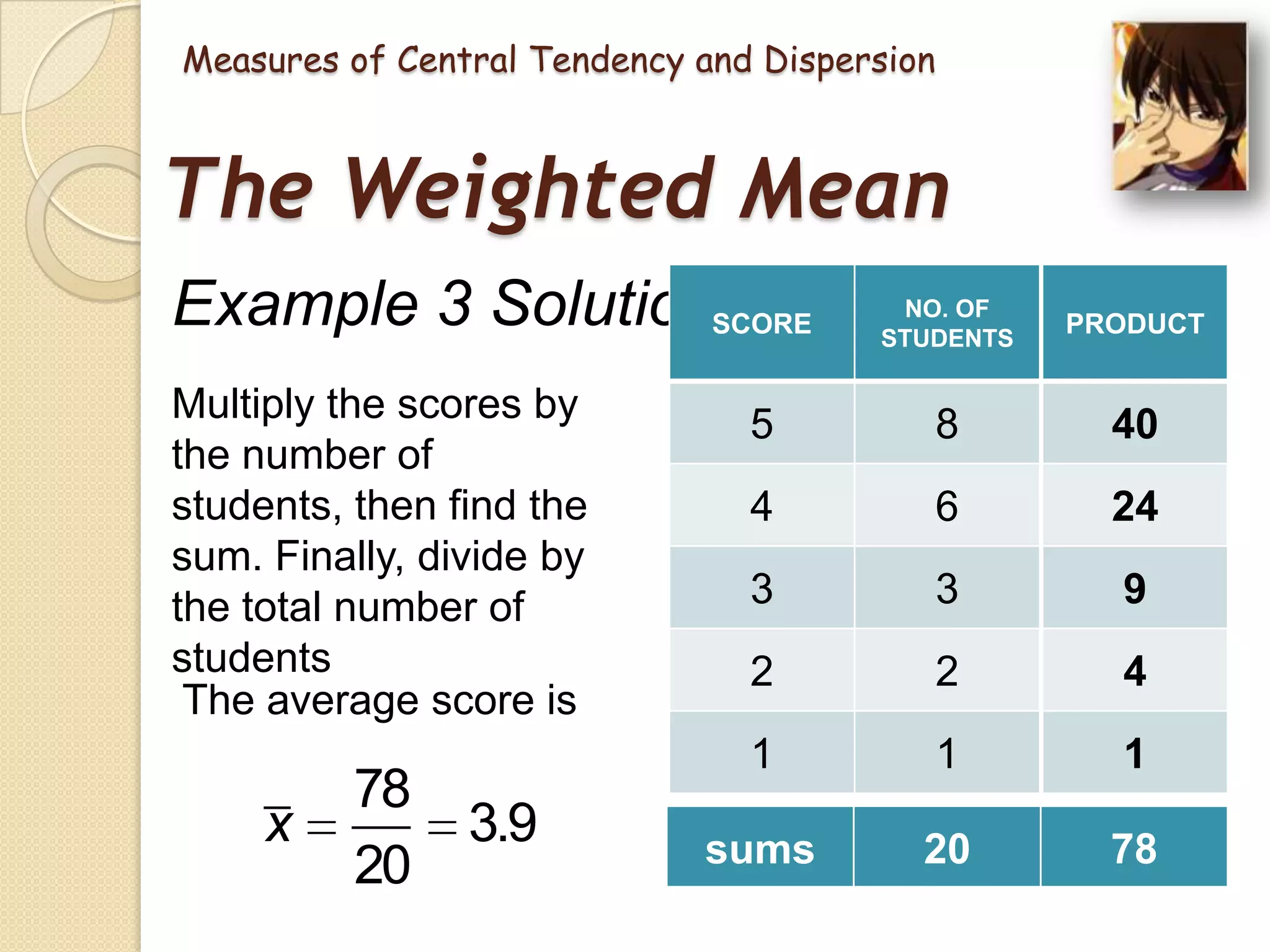
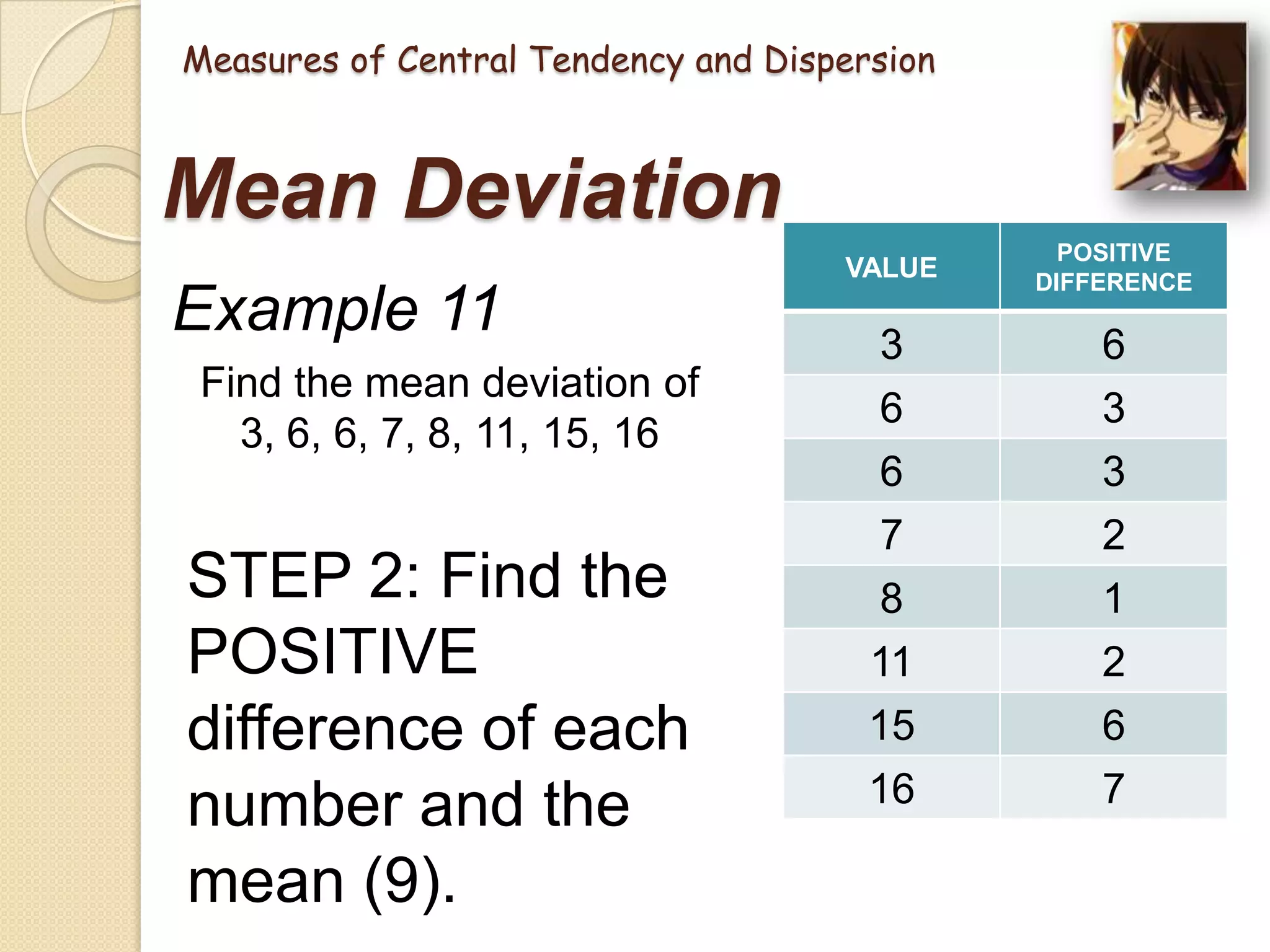
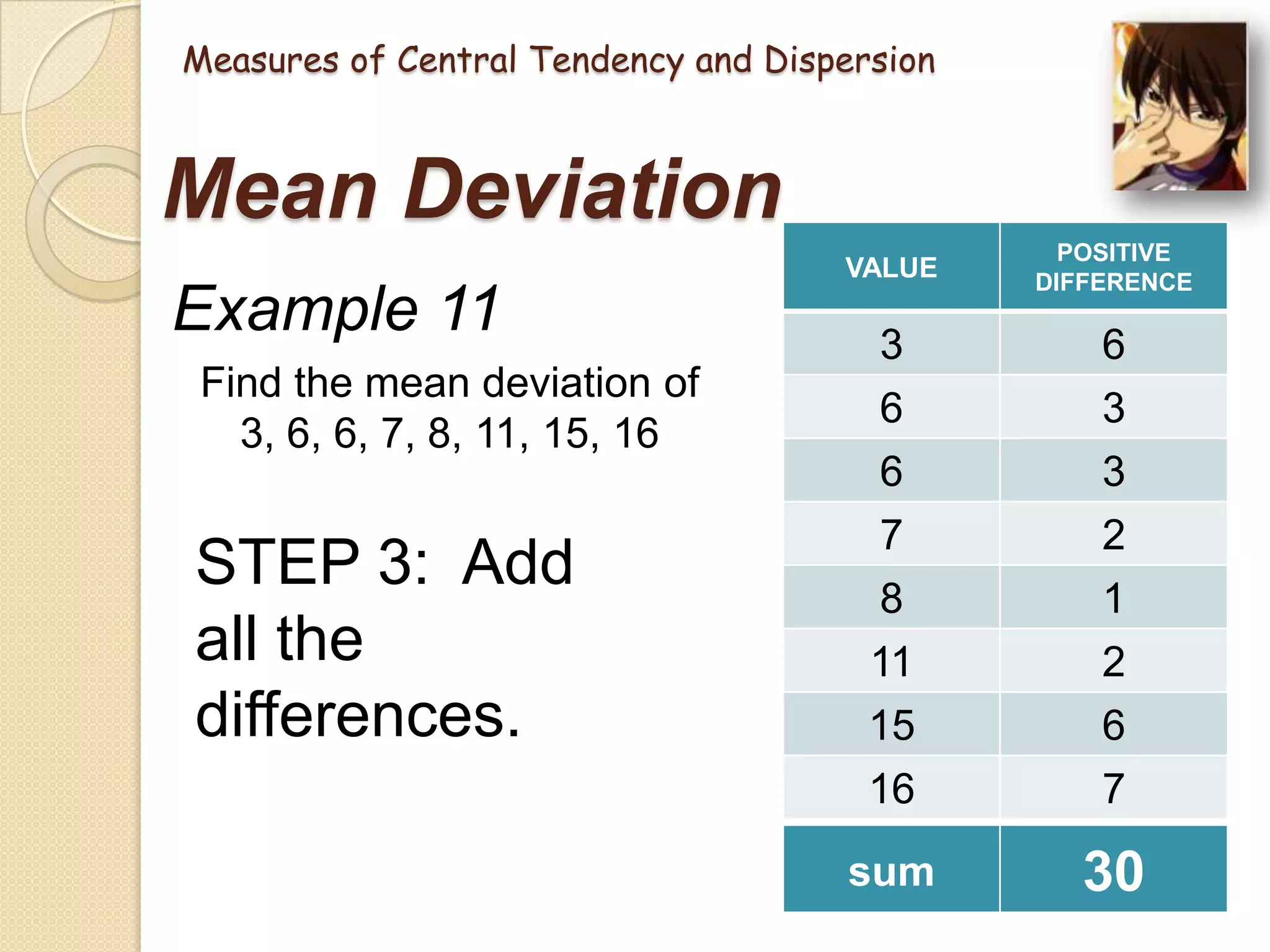
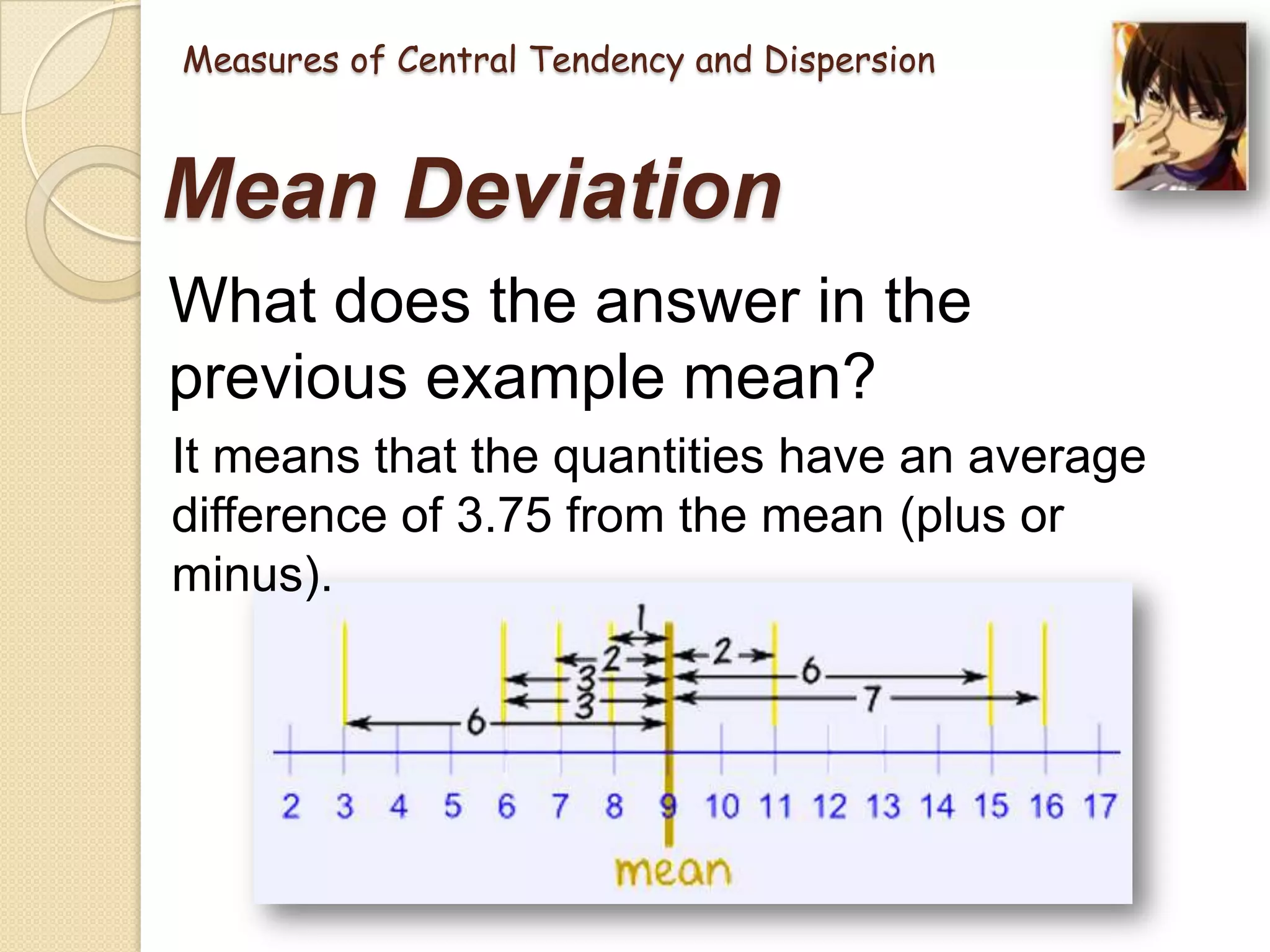
This document provides an introduction to statistics. It discusses what statistics is, the two main branches of statistics (descriptive and inferential), and the different types of data. It then describes several key measures used in statistics, including measures of central tendency (mean, median, mode) and measures of dispersion (range, mean deviation, standard deviation). The mean is the average value, the median is the middle value, and the mode is the most frequent value. The range is the difference between highest and lowest values, the mean deviation is the average distance from the mean, and the standard deviation measures how spread out values are from the mean. Examples are provided to demonstrate how to calculate each measure.

4. A Brief Introduction to Statistics
What is Statistics
What is Statistics?
1. The science that deals with the collection,
organization, presentation, analysis, and
interpretation of numerical data to obtain
useful and meaningful information
2. A collection of quantitative data pertaining
to a subject or group. Examples are blood
pressure statistics etc.

5. A Brief Introduction to Statistics
Branches of Statistics
Two branches of statistics:
1. Descriptive Statistics:
Describes the characteristics of a product or
process using information collected on it.
2. Inferential Statistics (Inductive):
Draws conclusions on unknown process
parameters based on information contained in
a sample.
Uses probability

6. A Brief Introduction to Statistics
Data
DATA is any quantitative or qualitative
information.
Types of Data:
1.
Quantitative – numerical information obtained
from counting or measuring (e.g. age, qtr.
exam scores, height)
2.
Qualitative – descriptive attributes that cannot
be subjected to mathematical operations (e.g.
gender, religion, citizenship)

7. Measures of Central Tendency and Dispersion
The Measures of Central
Tendency and Dispersion
Statistics use numerical values used to
summarize and compare sets of data.
 Measure of Central Tendency:
number used to represent the center or
middle set of a set of data
 Measure of Dispersion (or
Variability): refers to the spread of
values about the mean.

(i.e., how spread out the values are with respect to the mean)

8. The Measures of
Central Tendency

9. Measures of Central Tendency and Dispersion
Measures of Central
Tendency
The Measure of Central Tendency:
1. Mean - the (arithmetic) average (or
the sum of the quantities divided by the number of
quantities)
Median – the middle value of a set
of ordered data
3. Mode – number in a data set that
occurs most frequently
2.

10. Measures of Central Tendency and Dispersion
The Mean
It‘s known as the typical ―average.‖
 It is the most common measure of central
tendency.
 Symbolized as:
◦ x for the mean of a sample
◦ μ (Greek letter mu) for the mean of a
population
• It‘s equal to the sum of the quantities in the
data set divided by the number of quantities

x
x
n

11. Measures of Central Tendency and Dispersion
The Mean
Example 1
Find the mean of the numbers in the
following data sets:
a.
b.
3, 5, 10, 4, 3
x
3 5 10 4 3
5
85, 87, 89, 90, 91, 98 x
540
6
90
25
5
5

12. Measures of Central Tendency and Dispersion
The Mean
Example 2
The table on the right
shows the age of 13
applicants for a job in a
factory in EPZA. What is
the average age of the
applicants?
(Adapted from DOLE-BLES i-Learnstat
module on Measures of Central Tendency)
Solution: x
318
13
24.5

13. Measures of Central Tendency and Dispersion
The Weighted Mean
It is a mean where some values contribute
more than others.
 Each quantity is assigned a corresponding
WEIGHT

(e.g. frequency or number, units, per cent)

The weighted mean is equal to the sum of the
products of the quantities (x) and their
corresponding weights (w), divided by the sum
of the weights.
x
wx
w

14. Measures of Central Tendency and Dispersion
The Weighted Mean
Example 3
SCORE
NO. OF
STUDENTS
5
8
4
6
3
3
2
2
1
1
The table shows the scores
of 20 students in a 5-item
Math IV seatwork.
Find the average score of
the class.

15. Measures of Central Tendency and Dispersion
The Weighted Mean
Example 3 SolutionSCORE
x
78
20
3.9
PRODUCT
5
8
40
4
6
24
3
3
9
2
2
4
1
Multiply the scores by
the number of
students, then find the
sum. Finally, divide by
the total number of
students
The average score is
NO. OF
STUDENTS
1
1
sums
20
78

16. Measures of Central Tendency and Dispersion
The Median
Used to find the middle value (center) of a
distribution.
 Used when one must determine whether
the data values fall into either the upper
50% or lower 50% of a distribution.
 Used when one needs to report the
typical value of a data set, ignoring the
outliers (few extreme values in a data
set).

◦ Example: median salary, median home prices in a market

17. Measures of Central Tendency and Dispersion
The Median
How to find the median:


Order the data in increasing order.
If the number of data is ODD, the
median is the middle number.
If n is odd, the middle number in n observations is the
(n + 1)/2 th observation

If the number of data is EVEN, the
median is the mean of the two middle
numbers.
If n is even the middle number in n observations is the
average of the (n/2)th and the (n/2+1)th observation

18. Measures of Central Tendency and Dispersion
The Median
Example 4
Find the median of each set of data.
a. 1, 2, 2, 3, 3, 4, 4, 5, 5
b. 1, 2, 2, 3, 3, 4, 4, 4, 5, 5
Answers
a. Me = 3 (the 5th number)
b. The average of 5th and 6th numbers:
3 4
Me
2
3.5

19. Measures of Central Tendency and Dispersion
The Median
Example 5
Find the median of the following:
3, 5, 6, 10, 9, 8, 7, 8, 9, 10, 7, 2, 5, 7
Solution:
Arrange from lowest to highest:
2, 3, 5, 5, 6, 7, 7, 7, 8, 8, 9, 9, 10, 10
The median is 7.

20. Measures of Central Tendency and Dispersion
The Mode
It is the number that appears most
frequently in a set of data.
 It is used when the most typical
(common) value is desired.
 It is not always unique. A distribution
can have no mode, one mode, or more
than one mode. When there are two or
more modes, we say the distribution is
multimodal.

(for two modes, we say that the distribution is
bimodal)

21. Measures of Central Tendency and Dispersion
The Mode
Example 6
The table shows the
scores of 20 students in
a 5-item AP quiz.
SCORE
NO. OF
STUDENTS
5
6
4
7
3
4
What is the modal
score?
2
2
Answer: 4
1
1

22. Measures of Central Tendency and Dispersion
The Mode
Example 7
Find the mode of each set of data.
a.
1, 2, 2, 3, 3, 4, 4, 4, 5, 5 Mo = 4
a.
1, 2, 2, 3, 3, 3,4, 4, 4, 5, 5Mo = 3 and 4
a.
1, 2, 3, 4, 5
No mode

23. Measures of Central Tendency and Dispersion
The Mode
Example 8
Find the mode of the following:
3, 5, 6, 10, 9, 8, 7, 8, 9, 10, 7, 2, 5, 7
Solution:
Arrange from lowest to highest:
2, 3, 5, 5, 6, 7, 7, 7, 8, 8, 9, 9, 10, 10
The mode is 7.

24. Measures of Central Tendency and Dispersion
Check your understanding
4, 8, 12, 15, 3, 2, 6, 9, 8, 7
The data set above gives the waiting times
(in minutes) of 10 students waiting for a
bus. Find the mean, median, and mode of
the data set.

25. Measures of Central Tendency and Dispersion
Check your understanding
4, 8, 12, 15, 3, 2, 6, 9, 8, 7
The data set above gives the waiting times (in minutes)
of 10 students waiting for a bus. Find the mean, median,
and mode of the data set.
Solution
Arrange the data first in increasing order:
2, 3, 4, 6, 7, 8, 8, 9, 12, 15
Mean : x
74
10
7.4 min
Median : Me
Mode : Mo 8 min
7 8
2
7.5 min

26. The Measures of
Dispersion

27. Measures of Central Tendency and Dispersion
Measures of Dispersion
The Measure of Dispersion or Variability
1. Range – the difference of the largest
and smallest value
2. Mean Absolute Deviation – the
average of the positive differences
from the mean
3. Standard deviation – involves the
average of the squared differences
from the mean.
(related: variance)

28. Measures of Central Tendency and Dispersion
Range
Simply the difference between the largest and
smallest values in a set of data
 Useful for analysis of fluctuations and for
ordinal data
 Is considered primitive as it considers only
the extreme values which may not be useful
indicators of the bulk of the population.
 The formula is:

Range = largest observation - smallest observation

29. Measures of Central Tendency and Dispersion
Range
Example 10
Find the range of the following data sets:
a.
3, 5, 10, 4, 3
range 10 3 7
b.
85, 87, 89, 90, 91, 98
range 98 85 13
c.
3, 5, 6, 10, 9, 8, 7, 8, 9, 10, 7, 2, 5, 7
range 10 2 8

30. Measures of Central Tendency and Dispersion
Mean Deviation
It measures the ‗average‘ distance of each
observation away from the mean of the data
 Gives an equal weight to each observation
 Generally more sensitive than the range, since
a change in any value will affect it
 The formula is

MD
x x
n
x
where x is a quantity in the set,
and n is the number of data.
is the mean,

31. Measures of Central Tendency and Dispersion
Mean Deviation
To find the mean deviation:MD
1.
2.
x x
n
Compute the mean.
Get all the POSITIVE difference of each
number and the mean.
(It‘s the same as getting the absolute value of each difference)
3.
4.
Add all the results in step 2.
Divide by the number of data.

32. Measures of Central Tendency and Dispersion
Mean Deviation
Example 11
Find the mean deviation of
3, 6, 6, 7, 8, 11, 15, 16
Solution
x
STEP 1: Find the mean:
72
8
9

33. Measures of Central Tendency and Dispersion
Mean Deviation
VALUE
Example 11
Find the mean deviation of
3, 6, 6, 7, 8, 11, 15, 16
STEP 2: Find the
POSITIVE
difference of each
number and the
mean (9).
POSITIVE
DIFFERENCE
3
6
6
3
6
7
8
11
15
16
3
2
1
2
6
7

34. Measures of Central Tendency and Dispersion
Mean Deviation
VALUE
Example 11
Find the mean deviation of
3, 6, 6, 7, 8, 11, 15, 16
STEP 3: Add
all the
differences.
POSITIVE
DIFFERENCE
3
6
6
3
6
7
8
11
15
16
3
2
1
2
6
7
sum
30

35. Measures of Central Tendency and Dispersion
Mean Deviation
VALUE
Example 11
Find the mean deviation of
3, 6, 6, 7, 8, 11, 15, 16
STEP 4: Divide the result
by the number of data to
get the MD:
MD
30
8
3.75
POSITIVE
DIFFERENCE
3
6
6
3
6
7
8
11
15
16
3
2
1
2
6
7
sum
30

36. Measures of Central Tendency and Dispersion
Mean Deviation
What does the answer in the
previous example mean?
It means that the quantities have an average
difference of 3.75 from the mean (plus or
minus).

37. Measures of Central Tendency and Dispersion
Standard Deviation
Measures the variation of observations
from the mean
 The most common measure of
dispersion
 Takes into account every observation
 Measures the ‗average deviation‘ of
observations from the mean
 Works with squares of residuals, not
absolute values—easier to use in further


38. Measures of Central Tendency and Dispersion
Standard Deviation

The formula for the standard deviation
is
2
x x
n
where x is a quantity in the set,
x is the
mean, and n is the number of data.

39. Measures of Central Tendency and Dispersion
Variance
 The
variance is simply the square of
the standard deviation, or 2
Variance :
2
x x
n
2

40. Measures of Central Tendency and Dispersion
Standard Deviation
x x
To find the standard deviation:
n
1. Compute the mean.
2. Get the difference of each number and the
mean.
3. Square each difference
4. Add all the results in step 3.
5. Divide by the number of data.
6. Get the square root.
Note: If the VARIANCE is to be computed, skip
the last step.
2

41. Measures of Central Tendency and Dispersion
Standard Deviation
Population versus Sample Standard
Deviation
 The standard deviation used here is
called the POPULATION standard
deviation.
 For very large populations, the SAMPLE
standard deviation (s) is used. Its
2
formula is
x x
s
n 1

42. Measures of Central Tendency and Dispersion
Standard Deviation
Alternative Formula for the Standard
Deviation formula for standard deviation
 Another
uses only the sum of the data as well the
sum of the squares of the data. This is
n
x
2
x
n
2

43. Measures of Central Tendency and Dispersion
Standard Deviation
To find the standard deviation using the
alternative formula:
n x
x
n
1. Compute the squares of the data.
2. Get the sum of the data and the sum of the
squares of the data.
3. Multiply the sum of the squares by the
number of data, then subtract to the square
of the sum of the data.
4. Get the square root of the result in step 3.
5. Divide the result by the number of data.
2
2

44. Measures of Central Tendency and Dispersion
Standard Deviation
Example 12
Find the standard deviation of
3, 6, 6, 7, 8, 11, 15, 16
using the given and the alternative
formulas.
Solution
Before using the formulas, it‘s better to
tabulate all results.

45. Measures of Central Tendency and Dispersion
Standard Deviation
Using the given formula
x
x–x
x x
2
n
(x – x)2
3
–6
36
6
6
7
8
11
15
16
–3
–3
–2
–1
2
6
7
sum
9
9
4
1
4
36
49
148
x x
n
148
8
4.3
2

46. Measures of Central Tendency and Dispersion
Standard Deviation
Using the alternative formula
x
3
sum
x2
9
6
6
7
8
11
15
16
72
36
36
49
64
121
225
256
796
n
x2
x
2
n
n
x
2
x
2
n
8 796
72
2
8
1
,184
8
4.3
Ano ang
pipiliin
mo?

47. Measures of Central Tendency and Dispersion
Standard Deviation
Remark:
For both cases, the variance is simply
the square of the standard deviation.
The value2is 74
Woohoo…

48. Measures of Central Tendency and Dispersion
Check your understanding
Find the standard deviation
and variance of the following
data set:
4, 8, 12, 15, 3, 2, 6, 9, 8, 7

49. Measures of Central Tendency and Dispersion

50. Thank
you!