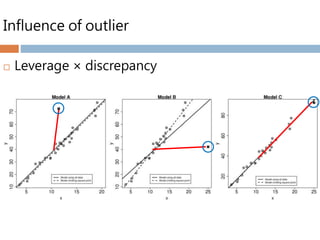
This document discusses important concepts for screening data, including detecting and handling errors, missing data, outliers, and ensuring assumptions of analyses are met. It describes why data screening is important to obtain accurate results and avoid bias. Key topics covered include identifying patterns of missing data, different types of missing data (MCAR, MAR, MNAR), and various methods for treating missing values. Outliers are defined and their impact explained. Common transformations are presented to achieve normality, linearity, and homoscedasticity. Checklists are provided for conducting data screening.

1. DATA SCREENING
Wei-Jiun, Shen Ph. D.

2. Anything that can
go wrong will go
wrong

3. Why do we need to
screen data?

4. Purpose
 Detect and correct data errors
 Detect and treat missing data
 Detect and handle insufficiently sampled variables
 Conduct transformations and standardizations
 Detect and handle outliers

5. First concern
 Accuracy of data file
 Descriptive statistics
 Graphic representations
 Honest correlations
 Missing data
 Pattern or amount
 Random or not
 Outliers

6. MISSING DATA
“blank” part in data set

7. Why is missing data a problem?
 Systematical problem
 Bias sampling
 Demographic variables
 Inappropriate measuring procedure
 Behavioral items
 Insufficient amount for analysis
 Small sample
 Misleading research results
 Biased data in, _______ out

8. Probability distribution of missingness
 Consider the probability of missingness
 Are certain groups more likely to have missing values?
 Respondents in female less likely to report age?
 Are certain responses more likely to be missing?
 Respondents with high SPA less likely to report anxiety?
 Certain analysis methods assume a certain probability
distribution

9. Missing completely at random (MCAR)
 Missing data is independent of any other
measured variable (y2) and independent of the
variable itself (y1)
 I.e., SES=y2; depression=y1.
 If participants dropped out across a range of SES
levels, then the missing on depression would be
independent of SES
 Little’s MCAR test in MVA indicates whether MCAR
or not (want ns)

10. Missing at random (MAR)
 Missing data may be dependent on another
measured variable (y2), but is independent of the
variable itself (y1).
 I.e., SES=y2; depression=y1.
 If participants only from high levels of SES dropped
out , then the missing on depression would be
dependent on SES. SES.
 MAR can be inferred if Little’s test is significant but
missingness predictable from other vars (other than
the variable itself) –tested by Separate Variance Test.
MNAR indicated if this test reveals missingness
related to the DV

11. Treatment for missing data
 Deleting cases or variables
 Descriptive statistics
 Estimating missing data
 Using missing data correlation matrix
 Treating missing data as data
 Repeating analyses with and without missing data
 Choosing among methods for dealing with
missing data
 Pattern or amount

12. Deletion or preservation?
 Deletion
 <5%
 MCAR/MAR
 Preservation
 MNAR
 Small sample
 Replacement
 Mean (grand or group)
 Regression (predict missing value by other IVs)
 Expectation Maximization (form missing data r matrix by
assumed distribution)

13. OUTLIER
Cases with extreme value on variables

14. Why is outlier a problem?
 Systematical problem
 Bias sampling
 Wrong population
 Statistical problem
 ↑error variance
 ↓statistical power
 ↑typeⅠ, Ⅱ error
 ↓normality
 Misleading research results
 Biased data in, _______ out

15. Influence of outlier
 Leverage × discrepancy

16. Treatment for outlier
 Estimating outlier
 Standardized score (z>2, 2.5, 3)
 Graphical methods (p-p, q-q plot)
 Mahalanobis distance (χ2 test)
 Deletion or transformation
 Critical to analysis or not
 Preservation
 Transformation
 Score alternation

17. NORMALITY,
LINEARITY &
HOMOSCEDASTICITY
Basic assumption

18. Key assumptions in GLM
 Normality
 Linearity
 Homogeneity of variance
 Interval level data
 Independence of observations

19. Normality
 Normal distribution

20. Test for normality
 Skewness & Kurtosis

21. Test for normality
 T-test for skewness & kurtosis score
 Kolmogorov-Smirnov test & Shaprio-wilk test
Z=
𝑠−0
𝑠 𝑠/𝑘
w=
( 𝑖=1
𝑛
𝑎 𝑖 𝑥 𝑖)
2
𝑖=1
𝑛
(𝑥 𝑖−𝐴)
2

22. Test for normality
 Plotting cumulative distribution function

23. Test for normality
 P-P plot (probability) & Q-Q plot (quantile)

24. Linearity
 Straight-line relationship between 2 variables

25. Homoscedasticity
 Homogeneity of variance
 Homogeneity of variance-covariance matrix

26. Homoscedasticity
 Residual

27. COMMON DATA
TRANSFORMATIONS

28. Data transformations
Directio
n
Skewness Treatment
+
Moderate New X = SQRT (X)
Substantial New X = LG10 (X)
Substantial with zero New X = LG10 (X+C)
Severe New X = 1/X
L-shaped with zero New X = 1 (X+C)
-
Moderate New X = SQRT (K-X)
Substantial New X = LG10 (K-X)
J-shaped New X = 1 (K-X)
C = a constant added to each score so that the smallest score is 1.
K = a constant from which each score is subtracted so that the smallest score is 1;
usually equal to the largest score + 1.

29. PRACTICE

30. Check list
 Descriptive statistics
 Range
 Mean & SD
 Skewness & kurtosis
 Missing data (missing value analysis)
 Normal distribution
 Kolmogorov-Smirnov test (n>50)
 Shapiro-Wilk test (n<50)
 Skewness & kurtosis
 PP plot
 Outlier (single/multiple: z-score/Mahalanobis distance)
 Linearilty
 Homoscedasticity
 Multiconllinearity

31. Report
 Try