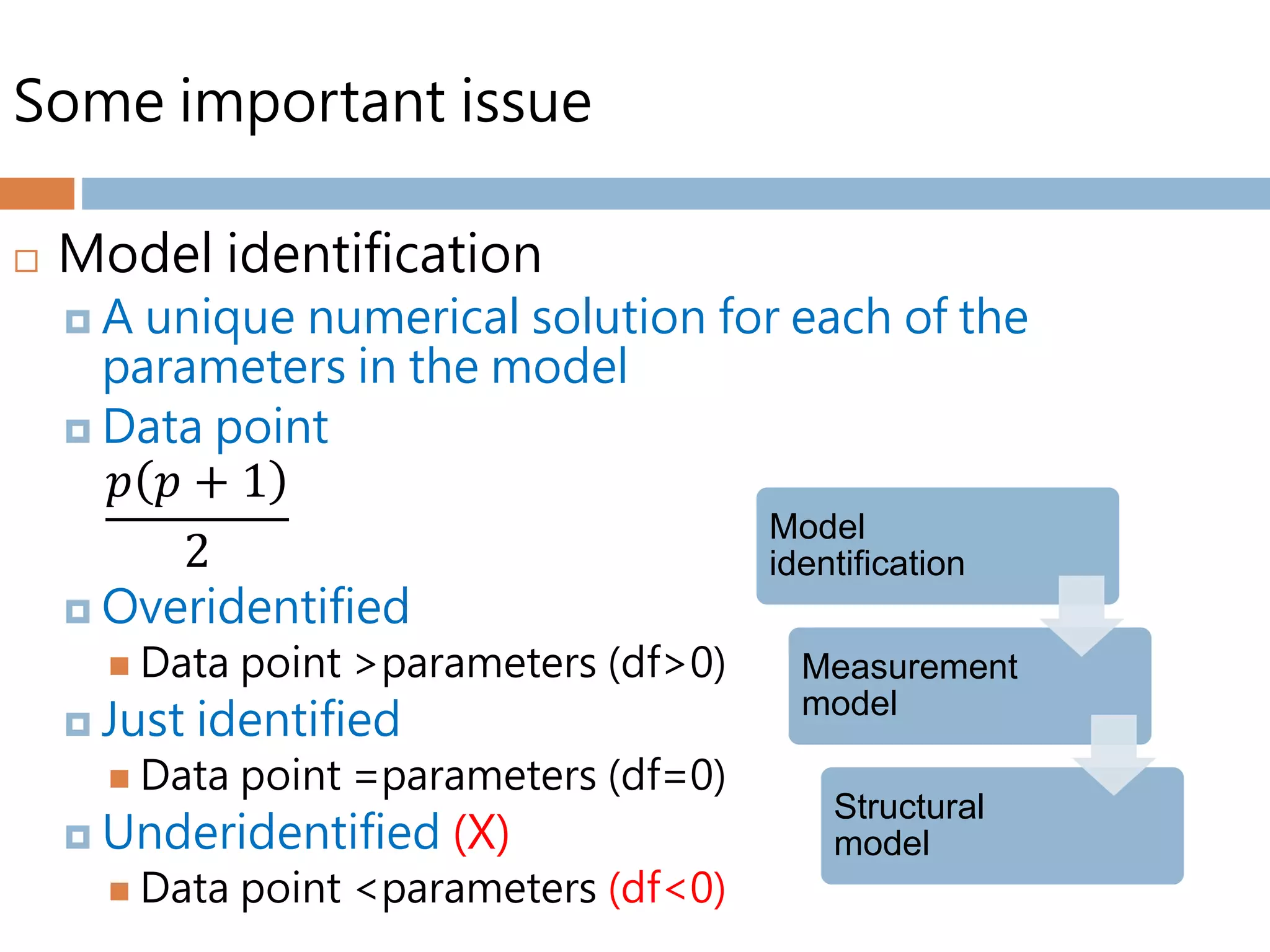
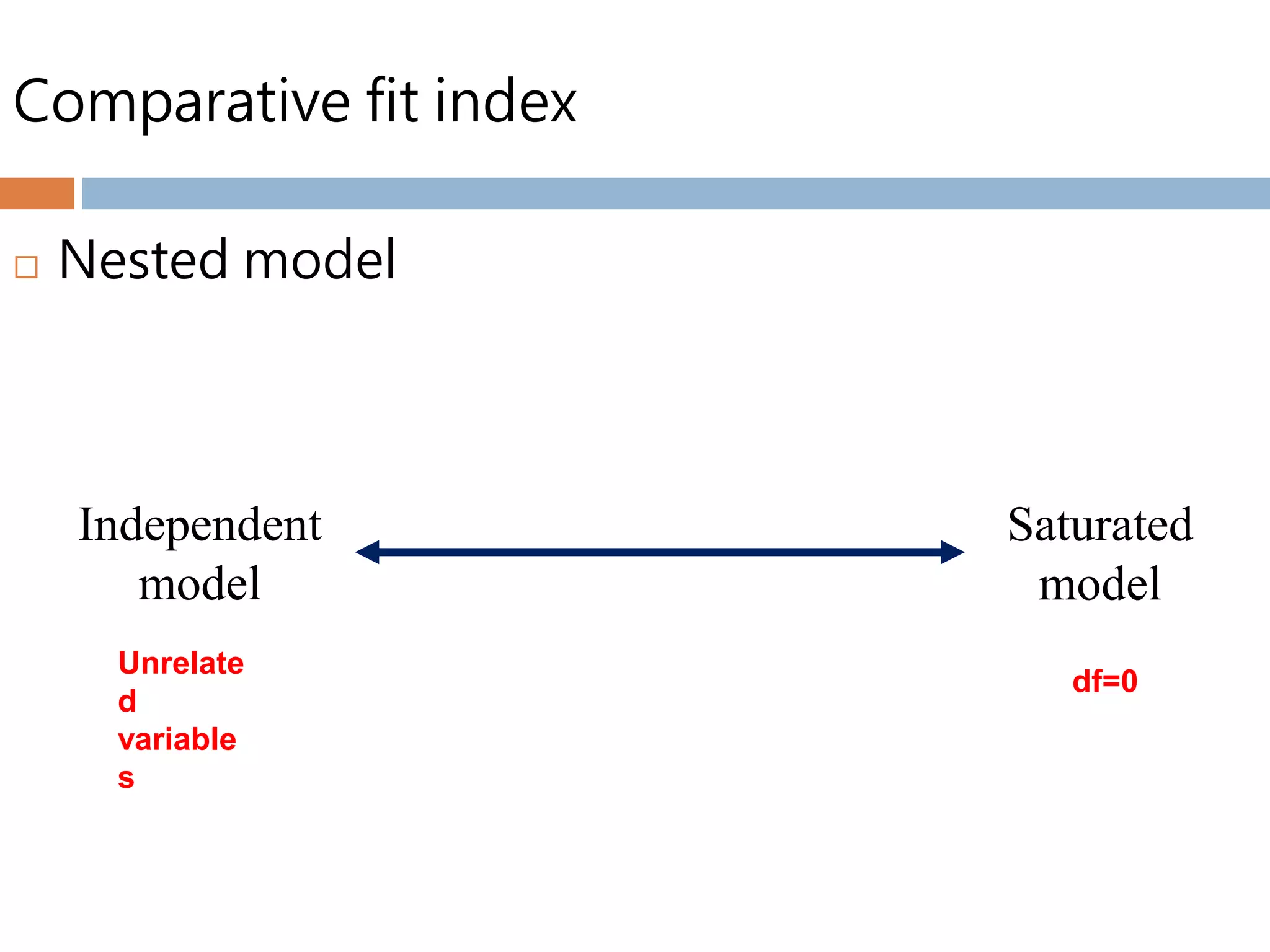
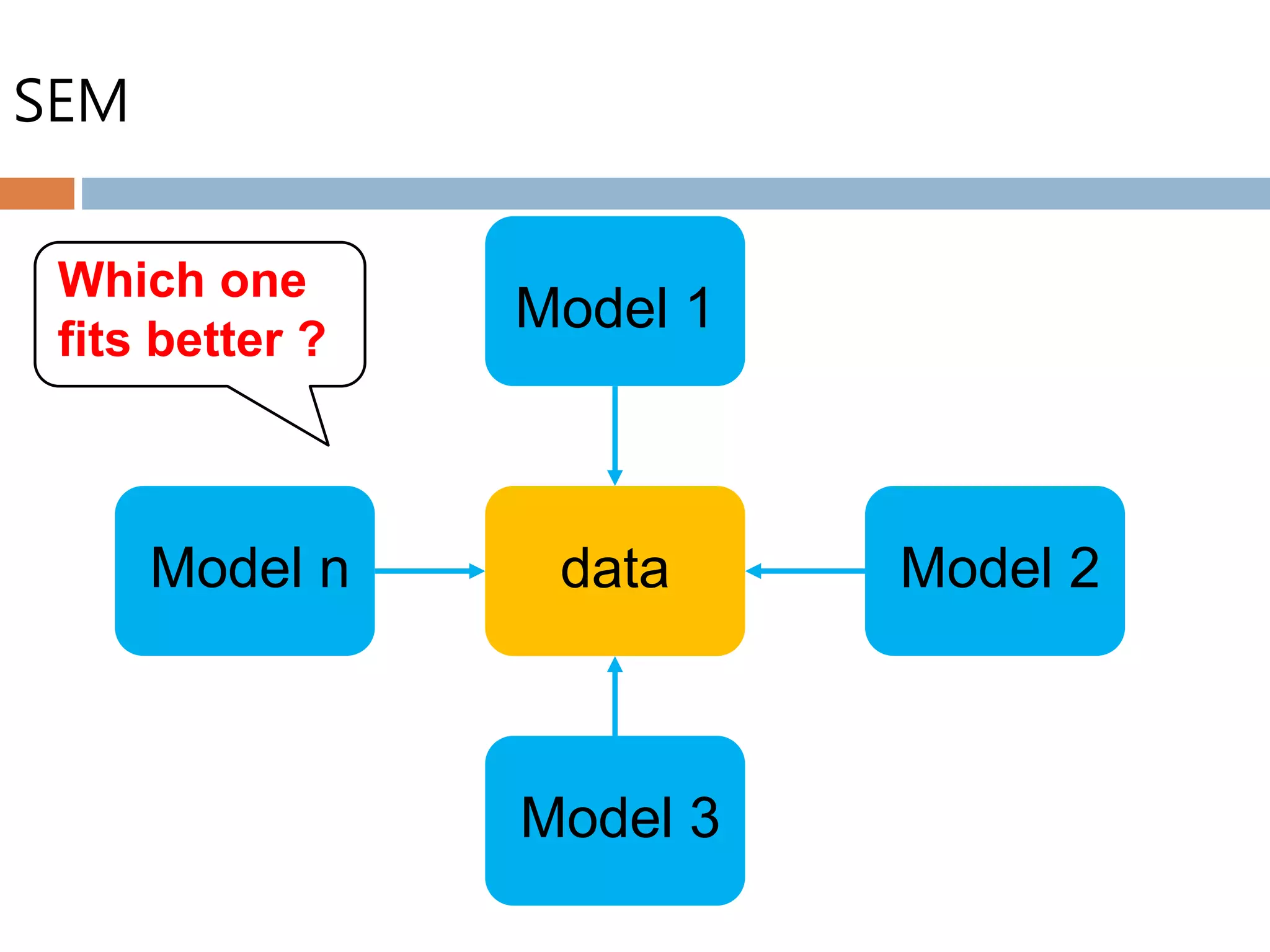
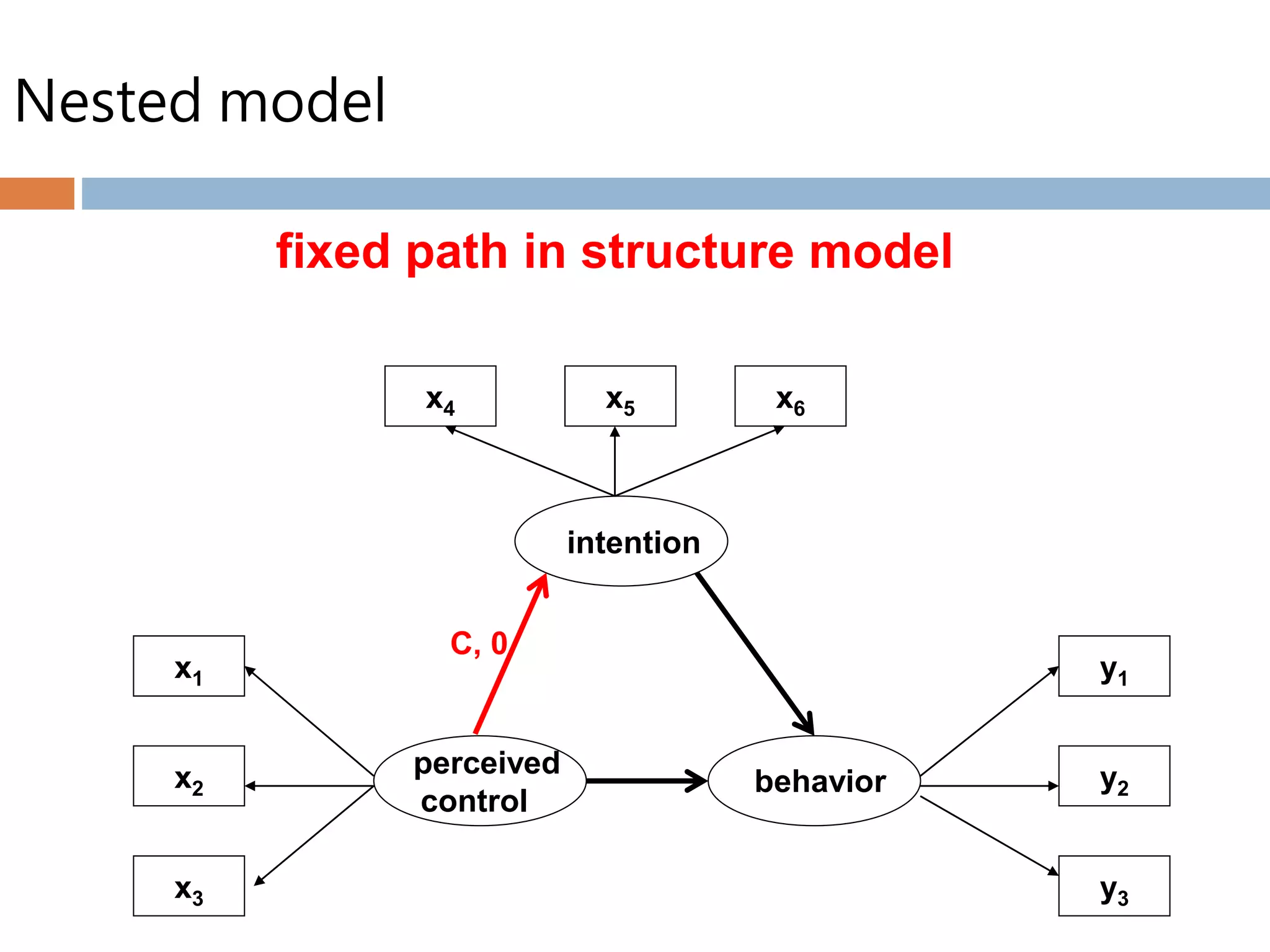
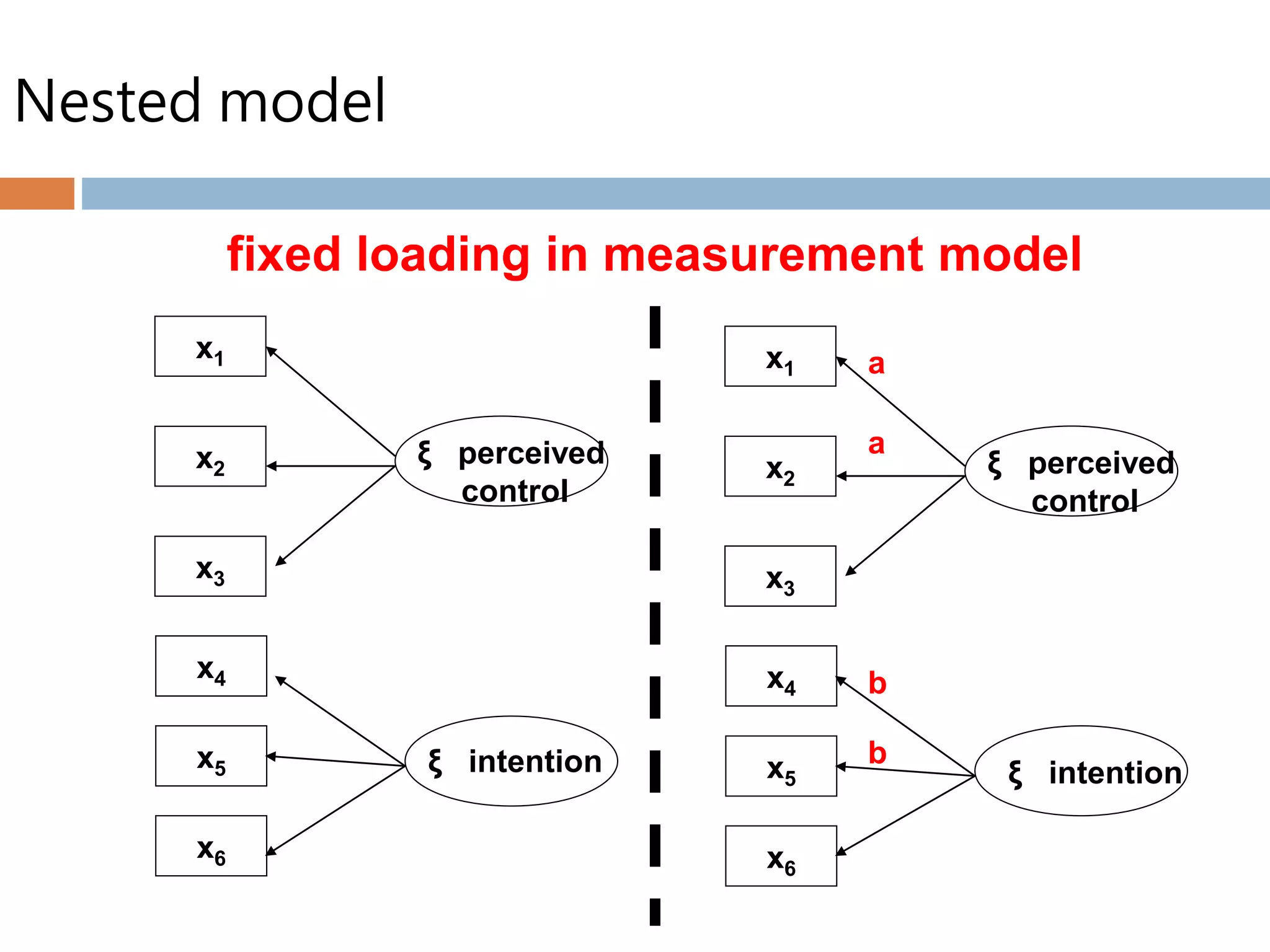
Structural equation modeling (SEM) is used to analyze relationships between multiple independent and dependent variables. It allows for simultaneous testing of these relationships while accounting for measurement error. The goal of SEM is to determine if the estimated population covariance matrix from the model fits the sample covariance matrix. It can be used to test theories, account for variance, and assess reliability and parameter estimates. Key considerations include sample size, normality, linearity, and identification of the model. Model fit is assessed using absolute, comparative, and parsimonious fit indices. Modification indices can also indicate how to improve model fit.

1. STRUCTURAL
EQUATIONS
MODELING (SEM)
Wei-Jiun, Shen Ph. D.

2. Purpose
 To analyze a set of relationships between one or
more IVs, either continuous or discrete, and one
or more DVs, either continuous or discrete.
 Multiple IVs
 Multiple DVs
 Confirmatory purpose
 Advantage
 Estimation of errors
 Simultaneous test

3. Kinds of research questions
 The goal of SEM is to examine whether the model
produce an estimated population covariance matrix
is fitted to the sample covariance matrix or not.
 Adequacy of model
 Testing theory
 Amount of variance in the variables accounted for by the
factors
 Reliability of the indicators
 Parameter estimates
 Intervening variables (indirect effect)
 Group difference
 Longitudinal difference
 Multilevel modeling

4. Limitations to factor analysis
 Theoretical issues
 Theory
 causality
 Practical issues
 Sample size and missing data
 15* umber of variable (Stevens, 1996)
 5* number of estimated parameter (Bentler & Chou, 1987)
 100 (Loehiln, 1992)
 Multivariate normality and outliers
 Linearity
 Absence of multicollinearity and singularity
 Residual

5. Fundamental equation for SEM
 Regression coefficients
 Variance-covariance matrices
 Data point
𝑌𝑗 = 𝛾𝑗𝑖 𝑋𝑖 + 𝜖1
𝐶𝑂𝑉 𝑋𝑖, 𝑌𝑗 = 𝐶𝑂𝑉(𝑋𝑖, 𝛾𝑗𝑖 𝑋𝑖 + 𝜖1)
= 𝛾𝑗𝑖 𝐶𝑂𝑉(𝑋𝑖, 𝑋𝑖)
= 𝛾𝑗𝑖 𝛿 𝑋 𝑖 𝑋 𝑖
η = 𝐵η + 𝛾ξ + ζ
𝑝 𝑝+1
2
variance +covariance

6. Graphical representation for SEM
x1
x2
x3
ξ belief η behavior
y1
y2
y3
δ１ ε１
λx1
γ
ζ
ε２
ε３
δ２
δ３
Error
Exogenous
observed
variable
Factor loading
Exogenous
latent variable
Structural parameter
Endogenous
latent variable
Factor loading
Endogenous
observed
variable
Structural
model
measurement
model
Error
λx2
λx3
λy1
λy2
λy3
measurement
model

7. Graphical representation for SEM
 Measurement model
 Confirmatory factor analysis (CFA)
x1
x3
x2
δ1
δ 2
δ 3
ξ1
λ11
λ21
λ31
δ[delta] ; λ[lambda]; ξ[xi]
x1= λ11 ξ1+ δ1
x2= λ21 ξ1+ δ2
x3= λ31 ξ1+ δ3

8. Some important issue
 Model identification
 A unique numerical solution for each of the
parameters in the model
 Data point
 Overidentified
 Data point >parameters (df>0)
 Just identified
 Data point =parameters (df=0)
 Underidentified (X)
 Data point <parameters (df<0)
𝑝 𝑝 + 1
2
Model
identification
Measurement
model
Structural
model

9. Assessing the fit of the model
Category Index
Absolute fit index
χ2, χ2/df
GFI
AGFI
Comparative fit index
RMSEA
CFI
NFI
NNFI
IFI
Parsimonious fit
index
PGFI
PNFI
CN
Residual
RMR
SRMR

10. Absolute fit index
 Chi-square test
 N.S.
 Chi-square / df < 2 (3)
 Indices of proportion of variance accounted
𝑔𝑜𝑜𝑑𝑛𝑒𝑠𝑠 − 𝑜𝑓 − 𝑓𝑖𝑡 𝑖𝑛𝑑𝑒𝑥 𝑮𝑭𝑰 =
𝑡𝑟( 𝜎′ 𝑊 𝜎)
𝑡𝑟(𝑠′ 𝑊𝑠)
𝑎𝑑𝑗𝑢𝑠𝑡𝑒𝑑 𝑔𝑜𝑜𝑑𝑛𝑒𝑠𝑠 − 𝑜𝑓 − 𝑓𝑖𝑡 𝑖𝑛𝑑𝑒𝑥 𝑨𝑮𝑭𝑰 =
1 − 𝐺𝐹𝐼
1 −
𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑒𝑠𝑡. 𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑟𝑠
𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑑𝑎𝑡𝑎 𝑝𝑜𝑖𝑛𝑡

11. Comparative fit index
 Nested model
Independent
model
Saturated
model
Unrelate
d
variable
s
df=0

12. Nested model
Phenome
na
Theor
y
Systematic
description
Data
Objectively
exist
Model
0
Framed by
theoretical
basement
fit or not
parameter estimation

13. Nested model
Saturated model
Model 1
Model 2
Model 3
Parent model or
Full model
all parameters are freely
estimated
restriction nested in
restriction nested in
restriction nested in
χ2 、df ↑

14. Comparative fit index
 Assessing the fit of the model
𝑐𝑜𝑚𝑝𝑎𝑟𝑎𝑡𝑖𝑣𝑒 𝑓𝑖𝑡 𝑖𝑛𝑑𝑒𝑥 𝑪𝑭𝑰 = 1 −
𝜏 𝑒𝑠𝑡.𝑚𝑜𝑑𝑒𝑙
𝜏𝑖𝑛𝑑𝑒𝑝.𝑚𝑜𝑑𝑒𝑙
𝜏 𝑒𝑠𝑡.𝑚𝑜𝑑𝑒𝑙 = χ𝑖𝑛𝑑𝑒𝑝.𝑚𝑜𝑑𝑒𝑙
2
− 𝑑𝑓𝑖𝑛𝑑𝑒𝑝.𝑚𝑜𝑑𝑒𝑙
𝜏 𝑒𝑠𝑡.𝑚𝑜𝑑𝑒𝑙 = χ 𝑒𝑠𝑡.𝑚𝑜𝑑𝑒𝑙
2
− 𝑑𝑓𝑒𝑠𝑡.𝑚𝑜𝑑𝑒𝑙
𝜏𝑖 = 𝑣𝑎𝑙𝑢𝑒 𝑜𝑓 𝑚𝑖𝑠𝑠𝑝𝑒𝑐𝑖𝑓𝑖𝑐𝑎𝑡𝑖𝑜𝑛
𝑟𝑜𝑜𝑡 𝑚𝑒𝑎𝑛 𝑠𝑞𝑢𝑎𝑟𝑒 𝑒𝑟𝑟𝑜𝑟 𝑜𝑓 𝑎𝑝𝑝𝑟𝑜𝑥𝑖𝑚𝑎𝑡𝑖𝑜𝑛 𝑹𝑴𝑺𝑬𝑨 =
𝐹0
𝑑𝑓 𝑚𝑜𝑑𝑒𝑙
𝐹0 =
χ 𝑚𝑜𝑑𝑒𝑙
2
− 𝑑𝑓 𝑚𝑜𝑑𝑒𝑙
𝑁
Compare to
independent
model
Compare to
saturated
model

15. Comparative fit index
𝑛𝑜𝑟𝑚𝑒𝑑 𝑓𝑖𝑡 𝑖𝑛𝑑𝑒𝑥 𝑵𝑭𝑰 =
χ𝑖𝑛𝑑𝑒𝑝
2
− χ 𝑚𝑜𝑑𝑒𝑙
2
χ𝑖𝑛𝑑𝑒𝑝
2
𝑛𝑜𝑛 − 𝑛𝑜𝑟𝑚𝑒𝑑 𝑓𝑖𝑡 𝑖𝑛𝑑𝑒𝑥 𝑵𝑵𝑭𝑰/𝑻𝑳𝑰 =
χ𝑖𝑛𝑑𝑒𝑝
2
−
𝑑𝑓𝑖𝑛𝑑𝑒𝑝
𝑑𝑓 𝑚𝑜𝑑𝑒𝑙
χ 𝑚𝑜𝑑𝑒𝑙
2
χ𝑖𝑛𝑑𝑒𝑝
2
− 𝑑𝑓𝑖𝑛𝑑𝑒𝑝
Underestimate with small N
Too sensitive to stable
𝑖𝑛𝑐𝑟𝑒𝑚𝑒𝑛𝑡𝑎𝑙 𝑓𝑖𝑡 𝑖𝑛𝑑𝑒𝑥 𝑰𝑭𝑰 =
χ𝑖𝑛𝑑𝑒𝑝
2
− χ 𝑚𝑜𝑑𝑒𝑙
2
χ𝑖𝑛𝑑𝑒𝑝
2
− 𝑑𝑓 𝑚𝑜𝑑𝑒𝑙

16. Parsimonious fit index
𝑝𝑎𝑟𝑠𝑖𝑚𝑜𝑛𝑦 𝐺𝐹𝐼 𝑷𝑮𝑭𝑰 = 1 −
𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑒𝑠𝑡. 𝑝𝑎𝑟𝑎𝑚𝑒𝑡𝑒𝑡𝑠
𝑛𝑢𝑚𝑏𝑒𝑟 𝑜𝑓 𝑑𝑎𝑡𝑎 𝑝𝑜𝑖𝑛𝑡𝑠
𝐺𝐹𝐼
𝐴𝑘𝑎𝑖𝑘𝑒 𝑖𝑛𝑓𝑜𝑟𝑚𝑎𝑡𝑖𝑜𝑛 𝑐𝑟𝑖𝑡𝑒𝑟𝑖𝑜𝑛 (𝑨𝑰𝑪) = χ 𝑚𝑜𝑑𝑒𝑙
2
− 2𝑑𝑓 𝑚𝑜𝑑𝑒𝑙
𝑐𝑜𝑛𝑠𝑖𝑠𝑡𝑒𝑛𝑡 𝐴𝑘𝑎𝑖𝑘𝑒 𝑖𝑛𝑓𝑜𝑟𝑚𝑎𝑡𝑖𝑜𝑛 𝑐𝑟𝑖𝑡𝑒𝑟𝑖𝑜𝑛 (𝑪𝑨𝑰𝑪) = χ 𝑚𝑜𝑑𝑒𝑙
2
− (𝑙𝑛𝑁 + 1)2𝑑𝑓 𝑚𝑜𝑑𝑒𝑙

17. Residual-based fit indices
 Average difference between sample and
estimated population variance-covariance
𝑟𝑜𝑜𝑡 𝑚𝑒𝑎𝑛 𝑠𝑞𝑢𝑎𝑟𝑒 𝑟𝑒𝑠𝑖𝑑𝑢𝑎𝑙 𝑹𝑴𝑹 = 2
𝑖=1
𝑞
𝑗=1
𝑖
𝑠𝑖𝑗 − 𝜎𝑖𝑗
2
𝑞 𝑞 + 1
1
2

18. Recommended value of index
Index Value
χ2 N.S.
Χ2/df <2 (3)
NFI >.95 (.90)
NNFI >.95 (.90)
IFI >.95 (.90)
CFI >.95 (.90)
GFI >.90
AGFI >.90
PGFI >.90
AIC Small
CAIC Small
RMSEA <.05 (.06)
SRMR <.08

19. What indices should be presented?
 Diamantopoulo & Siguaw (2000)
 χ2, χ2/df, RMSEA, SRMR, GFI/AGFI, CFI, ECVI
 Hoyle & Panter (1995)
 χ2, χ2/df, GFI/AGFI, CFI, NNFI, IFI, RNI

20. Model modification
 Chi-square difference test
 (χ2
2
− χ1
2
)/(𝑑𝑓2 − 𝑑𝑓1)
 Lagrange multiplier (LM) test
 Add parameters
 Wald test
 Delete parameters

21. CONFIRMATORY
FACTOR ANALYSIS
(CFA)

22. Application of SEM
 Measurement model
 Confirmatory factor analysis (CFA)
x1
x3
x2
δ1
δ 2
δ 3
ξ1
λ11
λ21
λ31
x1= λ11 ξ1+ δ1
x2= λ21 ξ1+ δ2
x3= λ31 ξ1+ δ3

23. Indices
 Goodness-of fit
 Factor loading (λ >.70)
 R2
 Convergent validity
 Composite reliability
 𝜌𝑐 =
λ 2
λ 2+ 𝜃
 Average variance extracted (AVE)
 𝜌 𝑣 =
λ2
λ 2+ 𝜃
 Discriminant validity

24. PRACTICE

25. 運動團隊默契量表的效化檢驗
 運動團隊默契會反應在三種向度上，分別是正確
的：
 1.任務知識
 2.能力評價
 3.情緒覺察
 請進行驗證性因素分析提供進一步的效度證據。

26. SEM
MODEL COMPARISON

27. SEM
Phenome
na
Theor
y
Systematic
description
Data
Objectively
exist
Model
0
Framed by
theoretical
basement
fit or not
parameter estimation

28. SEM
data
Model 1
Model 2
Model 3
Model n
Which one
fits better ?

29. Nested model
Saturated model
Model 1
Model 2
Model 3
Parent model or
Full model
all parameters are freely
estimated
restriction nested in
restriction nested in
restriction nested in
χ2 、df ↑

30. Nested model
fixed path in structure model
x1
x2
x3
perceived
control
behavior
y1
y2
y3
x4 x5 x6
intention
C, 0

31. Nested model
fixed loading in measurement model
x1
x2
x3
ξ perceived
control
x4
x5
x6
ξ intention
x1
x2
x3
ξ perceived
control
x4
x5
x6
ξ intention
a
a
b
b

32. Nested model
fixed correlation between latent variables
in measurement model
x1
x2
x3
ξ perceived
control
x4
x5
x6
ξ intention
x1
x2
x3
ξ perceived
control
x4
x5
x6
ξ intention
C, 0

33. Which one fits better?
 Nested model
 △χ2 test
 Target coefficient
 Initial model χ𝑖
2
 Restricted model χ 𝑟
2
 T= χ𝑖
2
/ χ 𝑟
2
 Non-nested model
 AIC
 CAIC

34. Parsimonious purpose
 General concept and multiple dimensions
 1 order
 2 order
 Nested model
 Required number of lower order dimension
 >3
 3 (equivalent model)

35. PRACTICE

36. 控制型教練領導行為量表的效化檢驗
 根據相關學理，教練的控制傾向會反應在四種向度
上，分別是：
 1.酬賞控制
 2.有條件式的關愛
 3.威嚇
 4.過度控制
 研究生康挫依中文化了控制型領導行為量表，請幫
他進行驗證性因素分析提供進一步的效度證據。

37. SEM
MEASUREMENT
INVARIANCE

38. Generalization
model
data 1
Population 1
fit
fit
Can we generalize the
psychological
phenomenon of P1 to P2 ?
Population 2
data 2
are the constructs comparable
between the two populations?
(mean, variance, covariance or
correlation)

39. Measurement invariance
 Measurement equivalence
 Construct comparability
 Advantage
 Identical operational definition
 Generalizability
 Minimize bias (culture, translation, or survey)
 However…

40. So, how
 Multiple group mean and covariance structure
analysis (MACS)(Little, 1997)
 Parameters (Meredith, 1993)
 Configural invariance
 Weak factorial invariance
 Strong factorial invariance
 Strict factorial invariance
 Structural invariance

41. Configural invariance
 Baseline model
𝑌1 = 𝑏0 + 𝑏11 𝑋1 + 𝑏21 𝑋2 + ⋯ + 𝑏 𝑝1 𝑋 𝑝 + 𝑒1
𝑌𝑞 = 𝑏0 + 𝑏1𝑞 𝑋1 + 𝑏2𝑞 𝑋2 + ⋯ + 𝑏 𝑝𝑞 𝑋 𝑝 + 𝑒 𝑞
⋮⋮ ⋮ ⋮ ⋮
intercept
(mean)
slope
(loading)
error
(Meredith, 1993)

42. Weak factorial invariance 𝜦 𝟏 = 𝜦 𝟐
 Measurement weight
𝑌1 = 𝑏0 + 𝑏11 𝑋1 + 𝑏21 𝑋2 + ⋯ + 𝑏 𝑝1 𝑋 𝑝 + 𝑒1
𝑌𝑞 = 𝑏0 + 𝑏1𝑞 𝑋1 + 𝑏2𝑞 𝑋2 + ⋯ + 𝑏 𝑝𝑞 𝑋 𝑝 + 𝑒 𝑞
⋮⋮ ⋮ ⋮ ⋮
intercept
(mean)
slope
(loading)
error
(Meredith, 1993)

43. Strong factorial invariance 𝝉 𝟏 = 𝝉 𝟐
 Mean
𝑌1 = 𝑏0 + 𝑏11 𝑋1 + 𝑏21 𝑋2 + ⋯ + 𝑏 𝑝1 𝑋 𝑝 + 𝑒1
𝑌𝑞 = 𝑏0 + 𝑏1𝑞 𝑋1 + 𝑏2𝑞 𝑋2 + ⋯ + 𝑏 𝑝𝑞 𝑋 𝑝 + 𝑒 𝑞
⋮⋮ ⋮ ⋮ ⋮
intercept
(mean)
slope
(loading)
error
(Meredith, 1993)

44. Strict factorial invariance 𝜽 𝟏 = 𝜽 𝟐
 Measurement residual
𝑌1 = 𝑏0 + 𝑏11 𝑋1 + 𝑏21 𝑋2 + ⋯ + 𝑏 𝑝1 𝑋 𝑝 + 𝑒1
𝑌𝑞 = 𝑏0 + 𝑏1𝑞 𝑋1 + 𝑏2𝑞 𝑋2 + ⋯ + 𝑏 𝑝𝑞 𝑋 𝑝 + 𝑒 𝑞
⋮⋮ ⋮ ⋮ ⋮
intercept
(mean)
slope
(loading)
error
(Meredith, 1993)

45. Structural invariance 𝝋 𝟏 = 𝝋 𝟐
 Variance and covariance
𝑌1 = 𝑏0 + 𝑏11 𝑋1 + 𝑏21 𝑋2 + ⋯ + 𝑏 𝑝1 𝑋 𝑝 + 𝑒1
𝑌𝑞 = 𝑏0 + 𝑏1𝑞 𝑋1 + 𝑏2𝑞 𝑋2 + ⋯ + 𝑏 𝑝𝑞 𝑋 𝑝 + 𝑒 𝑞
⋮⋮ ⋮ ⋮ ⋮
intercept
(mean)
slope
(loading)
error
(Meredith, 1993)

46. Model comparison-nested model
 Baseline model
 𝜦 𝟏 = 𝜦 𝟐
 𝜦 𝟏 = 𝜦 𝟐 + 𝝉 𝟏 = 𝝉 𝟐
 𝜦 𝟏 = 𝜦 𝟐 + 𝝉 𝟏 = 𝝉 𝟐 + 𝜽 𝟏 = 𝜽 𝟐
 𝜦 𝟏 = 𝜦 𝟐 + 𝝉 𝟏 = 𝝉 𝟐 + 𝜽 𝟏 = 𝜽 𝟐 + 𝝋 𝟏 = 𝝋 𝟐
(Meredith, 1993)
Configural invariance
Weak factorial
invariance
Strong factorial
invariance
Strict factorial
invariance
Structural invariance

47. Which one fits better?
 Nested model
 △χ2 test
 Fit index (Cheug & Rensvold, 2002; Little, 1997; McGaw & Joredkog, 1971)
 △ NNFI <.05 (.02)
 △ IFI <.05
 △CFI <.01
 △RFI <.05

48. PRACTICE

49. 運動正念量表的效化檢驗
 根據相關學理，運動員的正念特性會反應在三個
向度上，分別是：
 1.覺察
 2.再專注
 3.不評價
 研究生歐芷觀發展了一份測量工具，請幫她進行
性別不變性的檢驗。