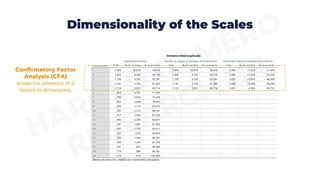
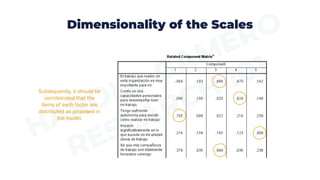
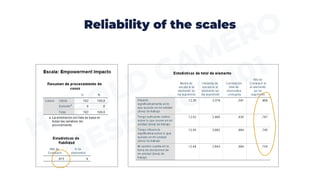
This document provides an overview of important steps in data preparation for research, including data coding, entry, checking for missing values and outliers, testing for normality, assessing dimensionality and reliability of scales. Specifically, it discusses coding survey responses numerically, entering data into statistical programs, identifying and addressing missing data, transforming variables as needed, identifying outlier data, testing data for normal distribution, confirming the dimensionality of multi-dimensional constructs using factor analysis, and calculating reliability coefficients of scales. The goal is to prepare data for statistical analysis and ensure it meets necessary assumptions of different statistical tests.

1. Research 101: Data Preparation
Harold Gamero

2. Data preparation
Data coding
Data entry
Missing values
Data transformation
Patterns in outlier data
Normality tests
Dimensionality of the scales
Reliability of the scales
1
2
3
4
5
6
7
8

3. Data Coding
• Coding is the process of converting data to numerical values.
• A codebook is a document that details the scales of each variable, the responses to each
item and what numerical values correspond to each response category.
• In some cases, it is possible to directly code the respondent's answer (age, income).
• Sometimes it is necessary to assign values to represent each variable (sex, profession).
• Qualitative results (such as interviews) cannot be “coded” and analysed statistically.

4. Data Coding

5. Data Entry
• Data can be entered into spreadsheets, databases or specialized statistical programs
(SPSS, Mplus, Stata, R, etc.).
• In the case of SPSS, rows represent individuals and columns represent variables, items
or response categories.
• The data entered should be constantly monitored for errors or invalid questionnaires (e.g.
meaningless patterns: all 1 or 5).
• Surveys with these errors should be discarded from further statistical analysis.

6. Missing Values
• Missing values may be unavoidable.
• Identify whether they appear randomly or show a pattern.
• If there is a pattern, the problem lies in the instrument or in the method applied (pilot
test).
• Examine the extent of the missing data.
• Select the way in which these values will be (not) used.
• By default, programs delete questionnaires with missing data (listwise deletion).
• Some allow the estimation and replacement of them (imputation).
• 2 types of unbiased imputation: maximum likelihood and multiple imputation methods.

7. Data Transformation
In some cases, data must be presented in a different way than collected.
For example:
➢ Scales that have items posed inversely
➢ Items that must be summed to obtain scores per dimension or variable
➢ Variables to be aggregated to obtain indexes
➢ Data that should be grouped into categories or ranges (age groups)

8. Patterns in Outlier Data
• Atypical data may appear due to:
➢ Errors in the data collection process
➢ Accumulated effect of external factors
➢ Extraordinary events
➢ Extraordinary remarks
• Outliers should be excluded from the analysis when they are an error (e.g., illogical or
erroneously entered responses).
• Outliers can be identified using steam & leaf plots.

9. Patterns in Outlier Data
Outliers
Less
dispersion
More
dispersion

10. Normality Test
• To use the normal statistical indicators (parametric statistics), we must verify that the
statistical assumptions are met.
• For this we can use:
Histograms Q-Q normality plots

11. Normality Test
• To use the normal statistical indicators (parametric statistics), we must verify that the
statistical assumptions are met.
• For this we can use:
Kolmogorov–Smirnov
test
Shapiro–Wilk test

12. Dimensionality of the Scales
• The next step is to verify that the items of our scales have been correctly distributed
across the dimensions of the construct of interest.
• For example, Empowerment is a multidimensional construct with 5 factors or
dimensions (Spreitzer, 1995):
➢ Meaning
➢ Competition
➢ Self-determination
➢ Impact
➢ Security

13. Dimensionality of the Scales
Confirmatory Factor
Analysis (CFA)
shows the presence of 5
factors or dimensions.

14. Dimensionality of the Scales
Subsequently, it should be
corroborated that the
items of each factor are
distributed as proposed in
the model.

15. Reliability of the scales
• We must confirm the reliability of the scales in our sample.
• Depending on the type of scale used, the method for calculating this indicator will be
different.
• For scales with additive Likert-type items, the recommended method is Cronbach’s
Alpha coefficient or the Composite Reliability Test
• In the case of multidimensional constructs, reliability coefficients are calculated per
dimension.
• Reliability coefficients can range from 0 to 1. Being 1 = perfect reliability, and 0 = null
reliability (Commonly, values above 0.7 are acceptable).

16. Reliability of the scales

17. Thank you.
Harold Gamero