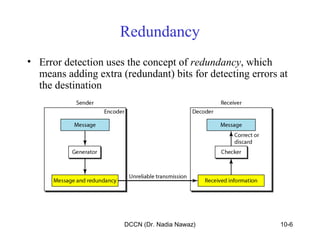
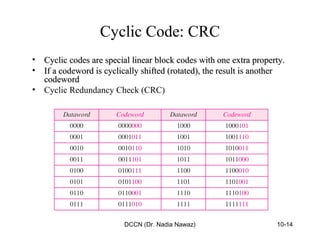
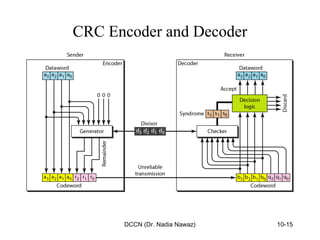
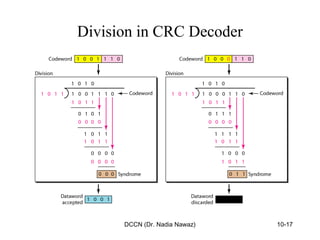
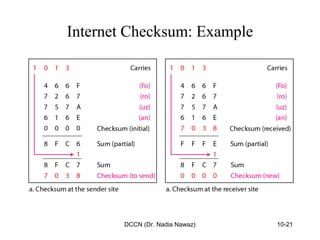
The document discusses error detection and correction in data communication, highlighting types of errors such as single-bit and burst errors. It covers methods for error control including redundancy, block coding, and cyclic codes, as well as checksum techniques for error checking. Additionally, it provides examples to illustrate how errors can be detected and corrected during data transmission.