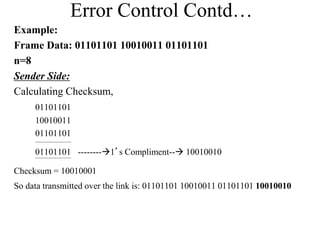
This document discusses different types of errors that can occur during data transmission and various error detection and correction techniques. It describes single-bit errors where one bit is changed and burst errors where multiple consecutive bits are changed. It then explains techniques like two-dimensional parity, checksums, and cyclic redundancy checks which add redundant bits to detect errors by checking for discrepancies between transmitted and received data. The document provides examples of how internet checksums and cyclic redundancy checks work to detect errors.

2. Types of Error
• Whenever bits flow from one point to another, they
are subject to unpredictable changes because of
interference and thermal noise.
Error Control

3. Single Bit Error
• single-bit error means that only 1 bit of a given data unit (such as
a byte, character, or packet) is changed from 1 to 0 or from 0 to1.
Burst Error
• The term burst error means that 2 or more bits in the data unit
have changed from 1 to 0 or from 0 to 1.
Error Control Contd…

4. Error Control
Error Control Contd…
Error Control
Error Detection Error Correction
Two Dimensional Parity
Internet Checksum
Cyclic Redundant Check (CRC)
Hamming Code

5. Error Detection Techniques
 Two approaches when the recipient detects an error
 Notify the sender that the message was corrupted, so the sender can
send again, if the error is rare, then the retransmitted message will
be error-free
 Using some error correct detection and correction algorithm, the
receiver reconstructs the message.
 Common technique for detecting transmission error
 CRC (Cyclic Redundancy Check)
 Used in HDLC, DDCMP, CSMA/CD
 Other approaches
 Two Dimensional Parity (used in BISYNC)
 Checksum (used in IP)
Error Control Contd…

6. Basic Idea of Error Detection
– To add redundant information to a frame that can be used
to determine if errors have been introduced
– Imagine (Extreme Case)
• Transmitting two complete copies of data
– Identical  No error
– Differ  Error
– Poor Scheme ???
» n bit message, n bit redundant information
» Error can go undetected
• In general, we can provide strong error detection technique
– k redundant bits, n bits message, k << n
– In Ethernet, a frame carrying up to 12,000 bits of data requires only 32-
bit CRC.
Error Control Contd…

7. TWO-DIMENSIONAL PARITY
 It is based on “simple” (one-dimensional) parity, which usually
involves adding one extra bit to a 7-bit code to balance the
number of 1s in the byte. For example,
 Odd parity sets the eighth bit to 1 if needed to give an odd number of
1s in the byte.
 Even parity sets the eighth bit to 1 if needed to give an even number
of 1s in the byte.
 Two-dimensional parity does a similar calculation for each bit
position across each of the bytes contained in the frame
 This results in an extra parity byte for the entire frame, in addition
to a parity bit for each byte
 Two-dimensional parity catches all 1-, 2-, and 3-bit errors and
most 4-bit errors
Error Control Contd…

8. Error Control Contd…

9. Internet Checksum:
Error Control Contd…
In internet checksum n=16

10.  Add up all the words that are transmitted and then transmit the
result of that sum
o The result is called the checksum.
 The receiver performs the same calculation on the received data
and compares the result with the received checksum
 If any transmitted data, including the checksum itself, is
corrupted, then the results will not match, so the receiver knows
that an error occurred
 Consider the data being checksummed as a sequence of 16-bit
integers.
• Add them together using 16-bit ones complement arithmetic and
then take the ones complement of the result. That 16-bit number
is the checksum.
• In ones complement arithmetic, a negative integer −x is
represented as the complement of x;
– Each bit of x is inverted.
Error Control Contd…

11.  When adding numbers in ones complement arithmetic, a
carryout from the most significant bit needs to be added to the
result (Wrapping).
Sender Side:
 The message is divided into 16-bit words.
 The value of the checksum word is set to 0.
 All words including the checksum are added using one's complement
addition.
 The sum is complemented and becomes the checksum.
 The checksum is sent with the data.
Receiver Side:
 The message (including checksum) is divided into 16-bit words.
 All words are added using one's complement addition.
 The sum becomes the new checksum.
 If the value of checksum is 0, the message is accepted; otherwise, it is
rejected.
Error Control Contd…

12. Example:
Frame Data: 01101101 10010011 01101101
n=8
Sender Side:
Calculating Checksum,
01101101
10010011
01101101
---------------------------
01101101 --------1’s Compliment-- 10010010---------------------------
Checksum = 10010001
So data transmitted over the link is: 01101101 10010011 01101101 10010010
Error Control Contd…

13. Receiver Side: (without Error)
Received Data: 01101101 10010011 01101101 10010001
Calculating Sum,
01101101
10010011
01101101
10010010
---------------------------
11111111 ----> All 1’s So accepted (No error)---------------------------
Receiver Side: (with Error)
Received Data: 11101101 10010011 01101101
11101101
10010011
01101101
10010010
---------------------------
01111111 ---> Not all 1’s. So not accepted (Contains Error)---------------------------
Error Control Contd…