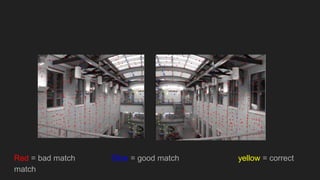
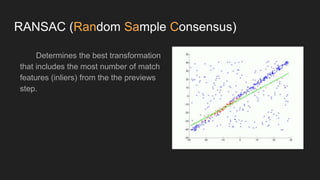
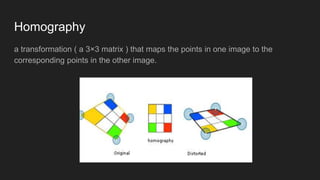
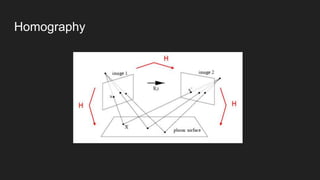
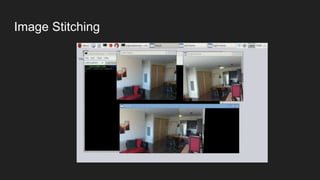
This document discusses feature matching and RANSAC algorithms. It begins by explaining feature matching, which determines correspondences between descriptors to identify good and bad matches. RANSAC is then introduced as a method to determine the best transformation that includes the most inlier feature matches. The document provides details on how RANSAC works including selecting random samples, computing transformations, and iteratively finding the best model. Applications like image stitching, panoramas, and video stabilization are mentioned.

1. Feature Matching w/
RANSAC
Autor | Calcaben | Obero

2. Previously on CMSC170
Feature Detection

3. Previously on CMSC170
Feature Detection

4. Previously on CMSC170
Feature Detection

5. Previously on CMSC170
Feature Descriptions

6. Previously on CMSC170
Feature Descriptions

7. Feature Matching w/
RANSAC
Autor | Calcaben | Obero

8. Feature Matching
Purpose: to determine correspondence between
descriptors in two views.
Strategy: which correspondences are passed on to
the next stage.

9. Feature Matching

10. Feature Matching

11. Measure difference as Euclidean distance between feature vectors:
Several possible matching strategies:
● Return all feature vectors with d smaller than a threshold.
● Nearest neighbor: feature vector with smallest d.
● Nearest neighbor distance ratio:
❖ d1, d2: distances to the nearest and 2nd nearest neighbors.
❖ If NNDR is small, nearest neighbor is a good match.
Feature Matching

15. Feature Matching
● Feature matching methods can give false matches.
● Manually select good matches, or use robust method to remove false
matches.
● Nearest neighbor search is computationally expensive.
○ Need efficient algorithm, e.g., using k-D Tree.
○ k-D Tree is not more efficient than exhaustive search for large
dimensionality, e.g., > 20.

17. Red = bad match Blue = good match yellow = correct
match

18. RANSAC (Random Sample Consensus)
Determines the best transformation
that includes the most number of match
features (inliers) from the the previews
step.

19. RANSAC (Random Sample Consensus)
RANSAC loop:
1. Select four feature pairs (at random)
2. Compute homography H (exact)
3. Compute inliers where SSD(pi’, Hpi) < ε
4. Keep largest set of inliers
5. Re-compute least-squares H estimate on all of the inliers

20. Homography
a transformation ( a 3×3 matrix ) that maps the points in one image to the
corresponding points in the other image.

21. Homography
Four corresponding points in
four different colors — red,
green, yellow and orange

22. Homography
Now since a homography is a 3×3 matrix we can write it as:
Let us consider the first set of corresponding points —(x1,y1) in the first image
and (x2,y2) in the second image. Then, the Homography H maps them in the
following way:

23. Homography

24. Pros and Cons

25. Pros
1. Simple and General
2. Applicable to many different problems
3. Often works well in practice
a. Robust estimation
b. Output acquire relatively high accuracy

26. Cons
1. Random Nature
2. Lots of Parameters to tune
3. High Computation Time
a. Number of iterations required
4. Can fail for extremely Low Inlier Ratios
a. Extremely sensitive to its threshold value

28. Applications

29. Image Stitching

30. Panorama

31. Long Screenshot
Screen #1
Screen #2
Screen #3
Screen #4
Screen #5
Screen #6

32. Video Stabilization

33. 360-degree image
Google Map - Street view

34. Code Demo

35. References
https://www.learnopencv.com/homography-examples-using-opencv-python-c/
https://docs.opencv.org/3.4.1/d9/dab/tutorial_homography.html
https://people.cs.umass.edu/~elm/Teaching/ppt/370/370_10_RANSAC.pptx.pdf