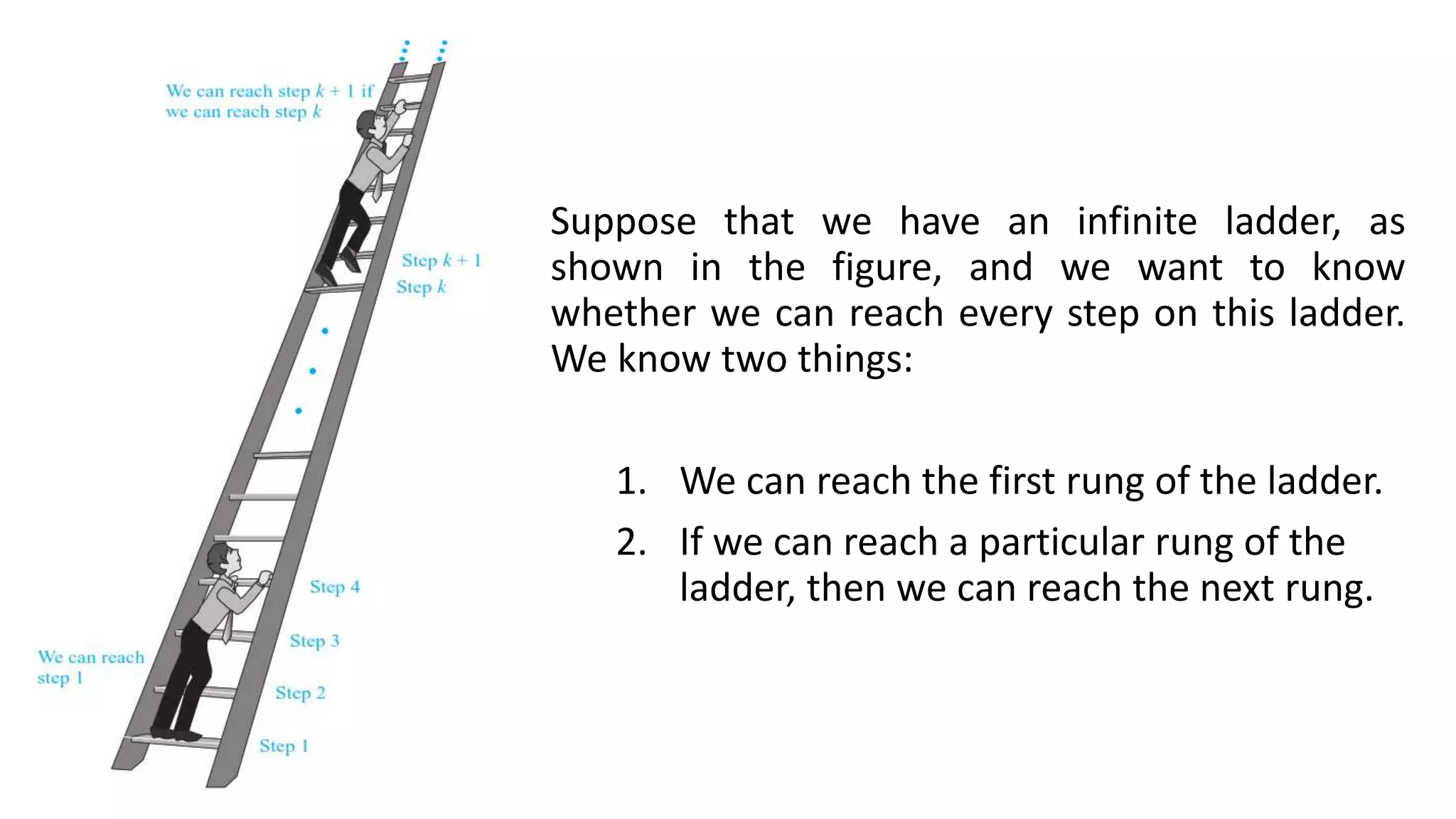
This document discusses the principles of mathematical induction, illustrating how to prove propositions for all positive integers using two main steps: the basis step and the inductive step. It includes examples such as reaching every rung of an infinite ladder and summation formulas to demonstrate the technique's applicability. Additionally, it highlights the limitations of mathematical induction and presents exercises for further practice.

1. Mathematical Induction
Lecture 11, CMSC 56
Allyn Joy D. Calcaben

2. Find the sum and the product of each pairs of numbers. Express
your answers as a binary expansion.
1. (100 0111)2 , (111 0111)2
2. (1110 1111)2 , (1011 1101)2
3. (10 1010 1010)2 , (1 1111 0000)2
Assignment (1 whole Sheet Paper)

3. Suppose that we have an infinite ladder, as
shown in the figure, and we want to know
whether we can reach every step on this ladder.
We know two things:
1. We can reach the first rung of the ladder.
2. If we can reach a particular rung of the
ladder, then we can reach the next rung.

4. Can we conclude that we are able to
reach every rung of this infinite
ladder?

5. The answer is yes, something we can verify using an important
proof technique called mathematical induction.

6. To prove that P(n) is true for all positive integers n, where P(n) is a
propositional function, we complete two steps:
Principle of Mathematical Induction

7. To prove that P(n) is true for all positive integers n, where P(n) is a
propositional function, we complete two steps:
Basis Step: We verify that P(1) is true.
Inductive Step: We show that the conditional statement
P(k) → P(k + 1) is true for all positive integers k.
Principle of Mathematical Induction

8. The assumption that P(k) is true is called the inductive hypothesis.
When we use mathematical induction to prove a theorem, we first
show that P(1) is true. Then we know that P(2) is true, because
P(1) → P(2). Further, we know that P(3) is true, P(2) → P(3).
Continuing along these lines, we see that P(n) is true for every
positive integer n.
Principle of Mathematical Induction

9. 1. We can reach the first rung of the ladder.
2. If we can reach a particular rung of the ladder, then we reach
the next rung.
Infinite Ladder

10. 1. We can reach the first rung of the ladder.
2. If we can reach a particular rung of the ladder, then we reach
the next rung.
Basis Step: Verify that P(1) is true.
Inductive Step: P(k) → P(k + 1) is true for all positive integers k
Therefore, P(n) is true for all positive integers n, where P(n) is the statement
that we can reach the nth rung of the ladder. Consequently, we can invoke
mathematical induction to conclude that we can reach every rung.
Infinite Ladder

11. How Mathematical Induction Works

12. “Domino Effect”
Step 1. The first domino falls
Step 2. When any domino falls, the next domino falls

13. “Domino Effect”
Step 1. The first domino falls
Step 2. When any domino falls, the next domino falls
….. all dominos will fall!
This is how Mathematical Induction works.

14. Example
There are infinitely many stations on a train route. Suppose
that the train stops at the first station and suppose that if the train
stops at a station, then is stops at the next station. Show that the
train stops at all stations.

15. Solution
Let P(n) be the statement that the train stops at station n.
Basis Step: We are told that P(1) is true.
Inductive Step: We are told that P(k) implies P(k+1) for each n ≥ 1.
Therefore by the principle of the mathematical induction, P(n) is
true for all positive integers n.

16. Proving Summation Formulae
Mathematical Induction is particularly well suited for proving that
such formulae are valid. However, summation formulae can be
proven in other ways.
major disadvantage of using mathematical induction:
1. you cannot use it to derive this formula.

17. Example
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2

18. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Let P (n) be the proposition that the sum of the first n positive integers, 1 + 2
+ ··· n =
𝑛 (𝑛+1)
2
, is
𝑛 (𝑛+1)
2
. We must do two things to prove that P (n) is true
for n = 1, 2, 3,.... Namely, we must show that P(1) is true and that the
conditional statement P(k)implies P(k+1) is true for k = 1, 2, 3,....

19. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Basis Step: P(1) is true, because 1 =
1 (1+1)
2

20. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Basis Step: P(1) is true, because 1 =
1 (1+1)
2
Inductive Step: We show that the conditional statement
P(k) → P(k + 1) is true for all positive integers k.

21. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Basis Step: P(1) is true, because 1 =
1 (1+1)
2
Inductive Step: First, assume P(k) is true for all positive integers k.

22. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Basis Step: P(1) is true, because 1 =
1 (1+1)
2
Inductive Step: First, assume P(k) is true for all positive integers k.
(Inductive Hypothesis)

23. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Basis Step: P(1) is true, because 1 =
1 (1+1)
2
Inductive Step: Inductive Hypothesis:
1 + 2 + . . . + 𝑘 =
𝑘 (𝑘+1)
2

24. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Basis Step: P(1) is true, because 1 =
1 (1+1)
2
Inductive Step: Under this assumption, it must be shown that
P(𝑘 + 1) is true.

25. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Basis Step: P(1) is true, because 1 =
1 (1+1)
2
Inductive Step: Under this assumption, it must be shown that
P(𝑘 + 1) is true.
1 + 2 + . . . + 𝑘 + (𝑘 + 1) =
𝑘+1 [(𝑘+1)+1]
2
=
𝑘+1 (𝑘+2)
2

26. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Basis Step: P(1) is true, because 1 =
1 (1+1)
2
Inductive Step: Add 𝑘 + 1 to both sides of the equation in P(𝑘)
P(𝑘): 1 + 2 + . . . + 𝑘 =
𝑘 (𝑘+1)
2

27. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Basis Step: P(1) is true, because 1 =
1 (1+1)
2
Inductive Step: Add 𝑘 + 1 to both sides of the equation in P(𝑘)
Left Side:
P(𝑘): 1 + 2 + . . . + 𝑘 =
𝑘 (𝑘+1)
2

28. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Basis Step: P(1) is true, because 1 =
1 (1+1)
2
Inductive Step: Add 𝑘 + 1 to both sides of the equation in P(𝑘)
Left Side:
P(𝑘): 1 + 2 + . . . + 𝑘 + (𝑘 + 1) =
𝑘 (𝑘+1)
2

29. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Basis Step: P(1) is true, because 1 =
1 (1+1)
2
Inductive Step: Add 𝑘 + 1 to both sides of the equation in P(𝑘)
Right Side:
P(𝑘): 1 + 2 + . . . + 𝑘 + (𝑘 + 1) =
𝑘 (𝑘+1)
2
+ (𝑘 + 1)

30. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Basis Step: P(1) is true, because 1 =
1 (1+1)
2
Inductive Step: Add 𝑘 + 1 to both sides of the equation in P(𝑘)
P(𝑘): 1 + 2 + . . . + 𝑘 + (𝑘 + 1) =
𝑘 𝑘+1 + 2 𝑘+1
2

31. Solution
Show that if 𝑛 is a positive integer, then
1 + 2 + . . . + 𝑛 =
𝑛 (𝑛+1)
2
Basis Step: P(1) is true, because 1 =
1 (1+1)
2
Inductive Step: Add 𝑘 + 1 to both sides of the equation in P(𝑘)
P(𝑘): 1 + 2 + . . . + 𝑘 + (𝑘 + 1) =
𝑘+1 𝑘+2
2

32. Example
Use mathematical induction to show that
1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for all nonnegative integers 𝑛.

33. Solution
Use mathematical induction to show that
1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for all nonnegative integers 𝑛.
Let P(𝑛) be the proposition that 1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for the integer 𝑛.

34. Solution
Use mathematical induction to show that
1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for all nonnegative integers 𝑛.
Basis Step: Let P(0) is true, because 20 = 1 = 2
1
− 1

35. Solution
Use mathematical induction to show that
1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for all nonnegative integers 𝑛.
Basis Step: Let P(0) is true, because 20 = 1 = 2
1
− 1
Inductive Step: Assume P(k) is true for an arbitrary nonnegative integer k.

36. Solution
Use mathematical induction to show that
1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for all nonnegative integers 𝑛.
Basis Step: Let P(0) is true, because 20 = 1 = 2
1
− 1
Inductive Step: Assume P(k) is true for an arbitrary nonnegative integer k.
(Inductive Hypothesis)

37. Solution
Use mathematical induction to show that
1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for all nonnegative integers 𝑛.
Basis Step: Let P(0) is true, because 20 = 1 = 2
1
− 1
Inductive Step: Inductive Hypothesis:
1 + 2 + 22 + . . . + 2 𝑘 = 2
(𝑘 + 1)
− 1

38. Solution
Use mathematical induction to show that
1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for all nonnegative integers 𝑛.
Basis Step: Let P(0) is true, because 20 = 1 = 2
1
− 1
Inductive Step: Under this assumption, it must be shown that P(𝑘 + 1) is
true.

39. Solution
Use mathematical induction to show that
1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for all nonnegative integers 𝑛.
Basis Step: Let P(0) is true, because 20 = 1 = 2
1
− 1
Inductive Step: Under this assumption, it must be shown that P(𝑘 + 1) is
true.
1 + 2 + 22 + . . . + 2 𝑘 + 2
(𝑘 + 1)
= 2
(𝑘 + 1) + 1
−1 = 2
(𝑘 + 2)
−1

40. Solution
Use mathematical induction to show that
1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for all nonnegative integers 𝑛.
Basis Step: Let P(0) is true, because 20 = 1 = 2
1
− 1
Inductive Step: Add 2
(𝑘 + 1)
to both sides of the equation in P(𝑘)
P(𝑘): 1 + 2 + 22 + . . . + 2 𝑘 = 2
(𝑘 + 1)
− 1

41. Solution
Use mathematical induction to show that
1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for all nonnegative integers 𝑛.
Basis Step: Let P(0) is true, because 20 = 1 = 2
1
− 1
Inductive Step: Add 2
(𝑘 + 1)
to both sides of the equation in P(𝑘)
Left Side:
P(𝑘): 1 + 2 + 22 + . . . + 2 𝑘 + 2
(𝑘 + 1)
= 2
(𝑘 + 1)
− 1

42. Solution
Use mathematical induction to show that
1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for all nonnegative integers 𝑛.
Basis Step: Let P(0) is true, because 20 = 1 = 2
1
− 1
Inductive Step: Add 2
(𝑘 + 1)
to both sides of the equation in P(𝑘)
Right Side:
P(𝑘): 1 + 2 + 22 + . . . + 2 𝑘 + 2
(𝑘 + 1)
= 2
(𝑘 + 1)
− 1 + 2
(𝑘 + 1)

43. Solution
Use mathematical induction to show that
1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for all nonnegative integers 𝑛.
Basis Step: Let P(0) is true, because 20 = 1 = 2
1
− 1
Inductive Step: Add 2
(𝑘 + 1)
to both sides of the equation in P(𝑘)
P(𝑘): 1 + 2 + 22 + . . . + 2 𝑘 + 2
(𝑘 + 1)
= 2 ⋅ 2
(𝑘 + 1)
− 1

44. Solution
Use mathematical induction to show that
1 + 2 + 22 + . . . + 2 𝑛 = 2
(𝑛 + 1)
− 1
for all nonnegative integers 𝑛.
Basis Step: Let P(0) is true, because 20 = 1 = 2
1
− 1
Inductive Step: Add 2
(𝑘 + 1)
to both sides of the equation in P(𝑘)
P(𝑘): 1 + 2 + 22 + . . . + 2 𝑘 + 2
(𝑘 + 1)
= 2
(𝑘 + 2)
− 1

45. 1. Prove that 12 + 32 + 52 + . . . + (2𝑛 + 1) 2 =
( 𝑛 + 1) (2 𝑛 + 1)(2 𝑛 + 3)
3
whenever 𝑛 is a nonnegative integer.
2. Prove that 3 + 3 ⋅ 5 + 3 ⋅ 52 + . . . + 3 ⋅ 5n =
3(5
𝑛 +1
− 1)
4
whenever
𝑛 is a nonnegative integer.
Challenge (1/2 Sheet Paper)