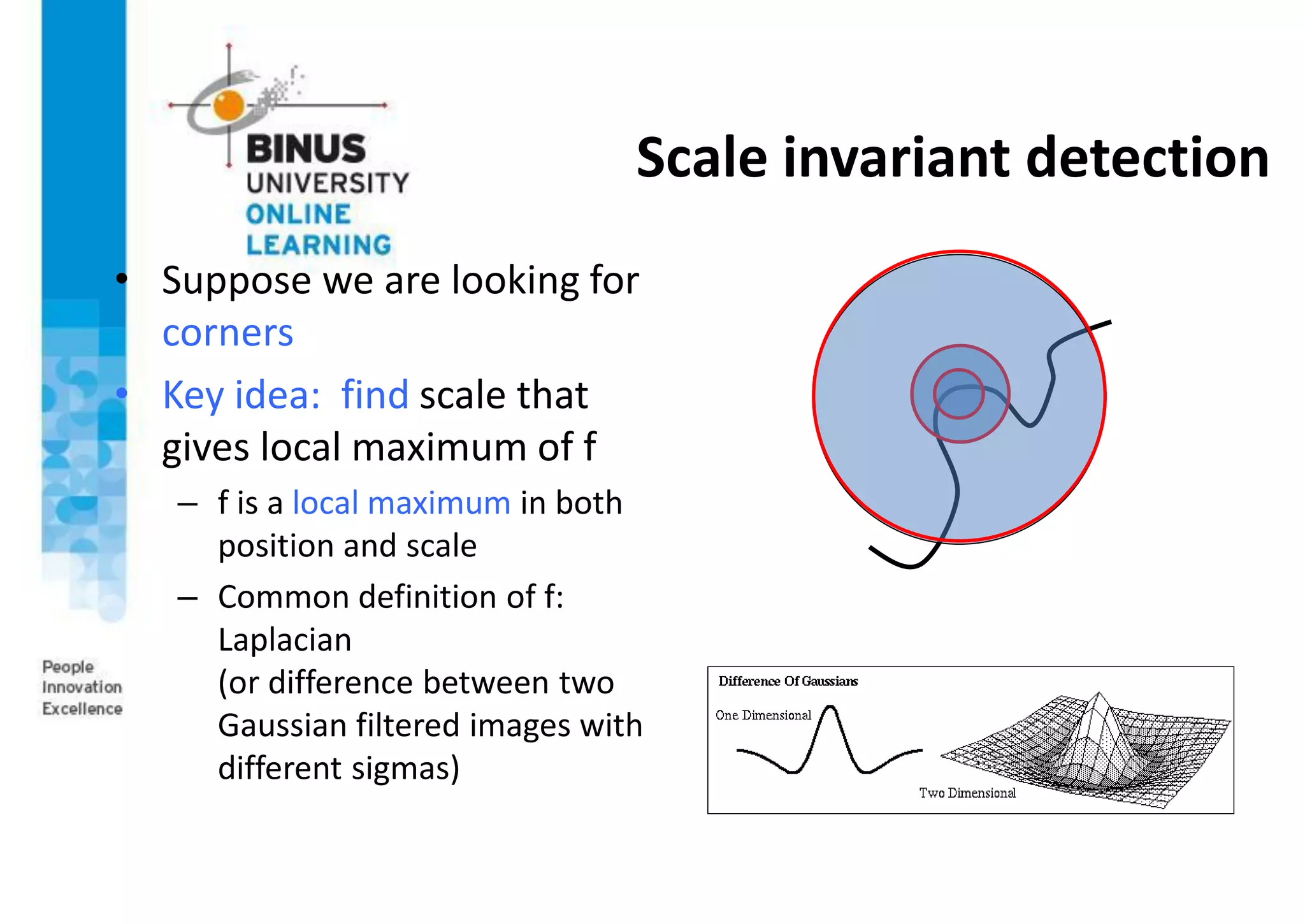
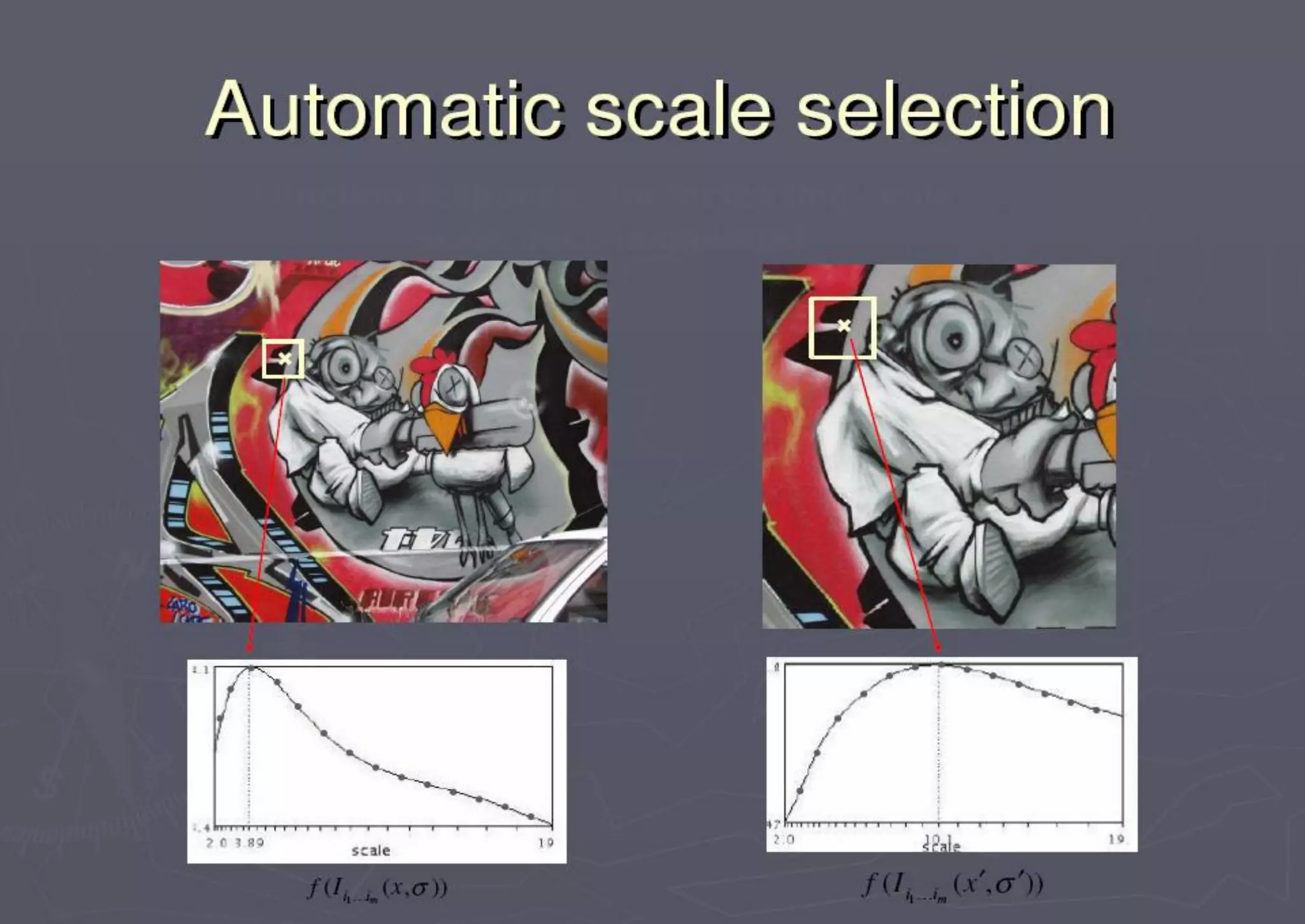
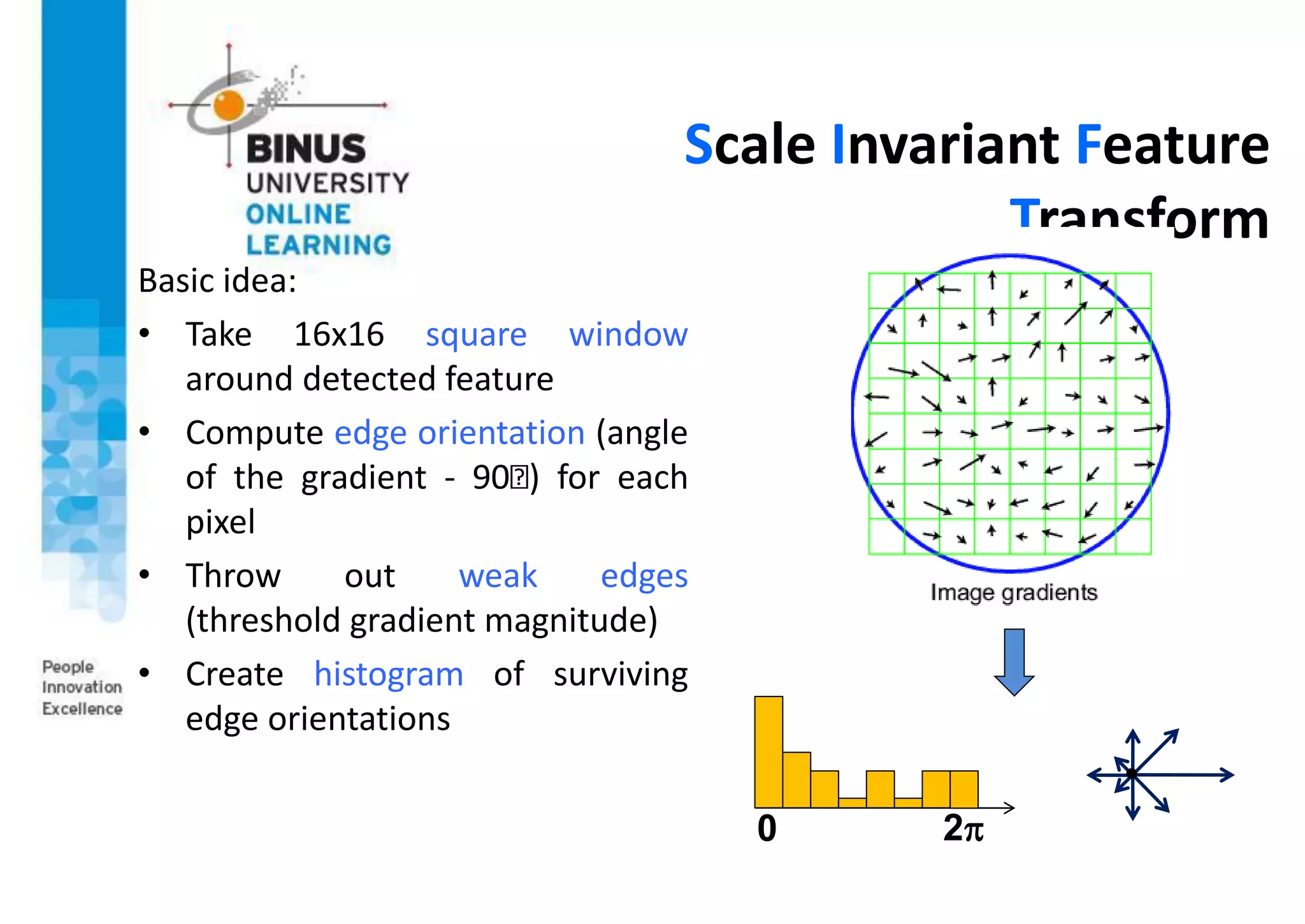
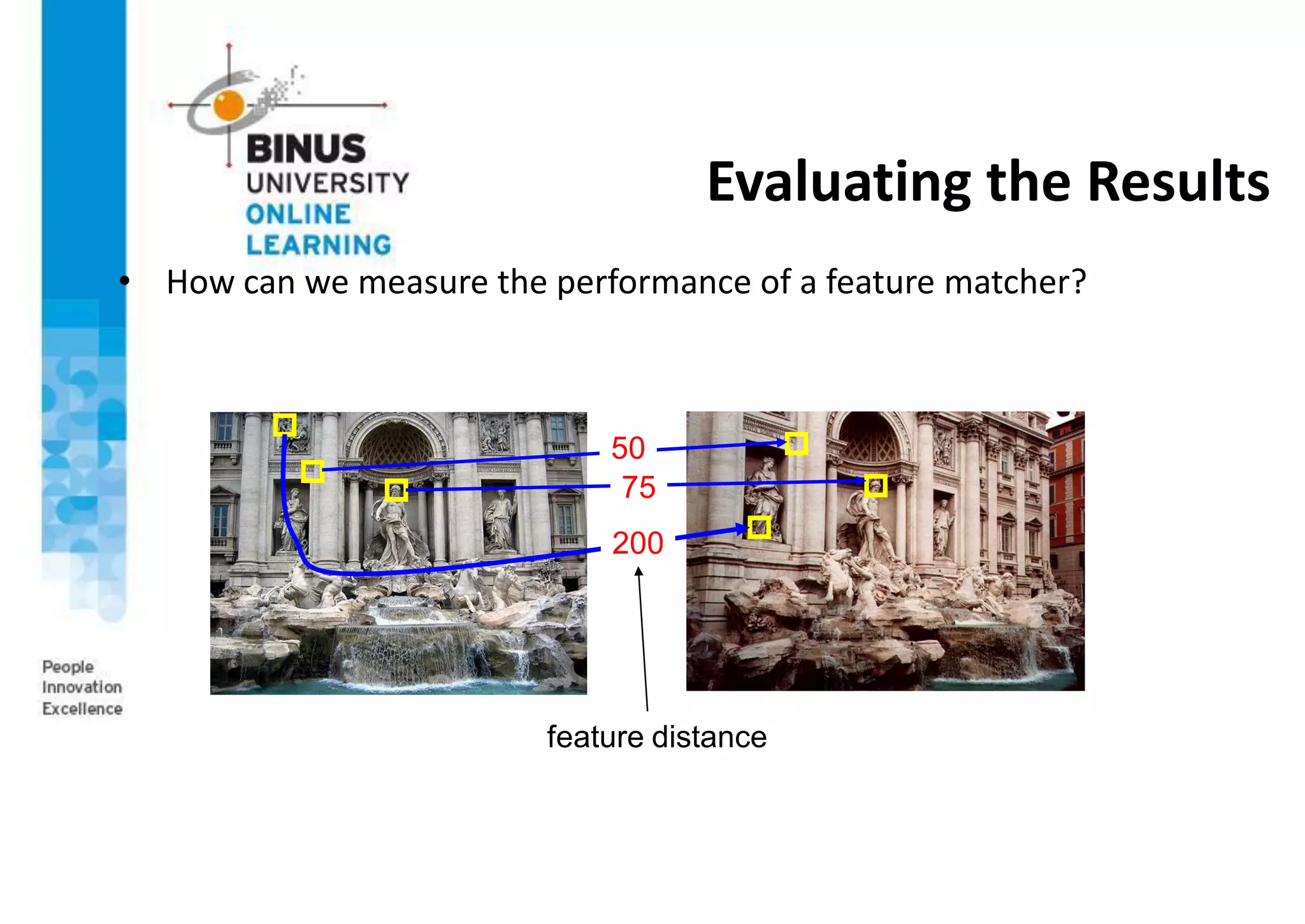
This document provides an overview of image matching techniques. It defines image matching as geometrically aligning two images so corresponding pixels represent the same scene region. Key aspects covered include detecting invariant local features, describing features in a scale and rotation invariant way using SIFT, and matching features between images. SIFT is highlighted as an extraordinarily robust technique that can handle various geometric and illumination changes. Feature matching is used in many computer vision applications such as image alignment, 3D reconstruction, and object recognition.