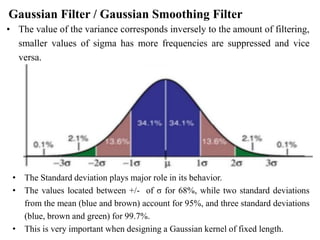
The document covers image processing, defining types of images, image formation, and various noise types encountered in images. It details noise reduction techniques and filtering methods such as mean, median, and Gaussian filters to address different types of noise like salt and pepper, Gaussian, and periodic noise. The document also discusses adaptive filtering methods and their advantages in processing images with varying impulse noise densities.

1. Image Processing
Dr. P. Kuppusamy

2. Content
• Types of images
• Image Processing Definition
• Digital Image
• Image Formation
• Types of digital images
• Histogram
• Noise in images
• Types of noise in image
• Salt and pepper noise / Impulse noise/ Shot noise / Spike noise
• Gaussian noise
• Uniform noise
• Rayleigh noise
• Erlang (Gamma) noise
• Exponential noise (Gamma Noise)

3. Content
• Noise removal filters
• Arithmetic and geometric mean filters
• Contraharmonic filters
• Mean / average filter
• Median filter
• Adaptive median Filters
• Max and min filter
• Midpoint filter
• Alpha trimmed mean filter
• Gaussian Filter / Gaussian Smoothing Filter
• Band Reject Filters
• Inverse filter
• Maximum Mean Square Error (Wiener) Filtering

4. Two Types of Images
1. Vector Images – Images made up of vectors which lead through locations
called control points. Each of these control points defined on the X and Y axes
of the work plain.
2. Digital Images - A digital image is an 2 dim-array of real numbers. 2-D
image is divided into N-rows and M-columns.
The intersection of these rows & columns is known as pixels.

5. Digital image is formation
• Capturing an image from a camera is a physical process. The
sunlight is used as a source of energy.
• A sensor array is used for the acquisition (digitization) of the
image.
• When the sunlight falls upon the object, the amount of light
reflected by that object is sensed by the sensors, and a continuous
voltage signal is generated by the sensed data.
• To create a digital image, convert this data into a digital form. This
involves sampling and quantization.
• The result of sampling and quantization is two dimensional array
or matrix of numbers is called a digital image.

6. Image processing
• Image processing is a method to perform some operations on an
image, like enhancing the image or extract some useful information
from the image.
• It is a type of signal processing in which input is an image and
output may be image or characteristics/features of the image.
Two types of methods:
1. Analogue image processing – It can be used for the hard copies
like printouts and photographs.
2. Digital image processing - use of a digital computer to process
digital images through an algorithm.

7. Digital Image
• An image is a two dimensional signal. It is defined by the mathematical function
f(x,y) where x and y are the two spatial (plane) co-ordinates horizontally and
vertically.
– The amplitude of f at pair of (x,y) is intensity of the image.
– If x, y and amplitude values of f are finite, it is called digital image.
– An image can be defined by a two-dimensional array specifically arranged
in rows and columns.
– The value of f(x,y) at any point gives the pixel value at that point of an
image.
– Each pixel has a particular location and value.
• f(x,y) = H(x,y) + B(x,y),
• f(x,y) = function of noisy image, H(x,y)= function of image noise , B(x,y)= function of
original image.
• Theoretically, a picture is a function of image intensity at a particular position
in the image. i.e I(x,y) is an image function where I = Intensity at position
(x,y) in an image.

8. Images as functions

9. f(1,1) = 103
83 82 82 82 82 82
82 82 82 81 81 81
82 82 81 81 80 80
82 82 81 80 80 79
80 79 78 77 77 77
80 79 78 78 77 77
f(2724,2336) = 88
f(645:650,1323:1328) =
Pixel intensity value
Pixel location
In 8-bit representation,
Pixel intensity values change
between 0 (Black) and 255
(White)
rows columns
Consider the image (2724x2336 pixels) to be 2D function or a matrix with
rows and columns

10. Types of digital images
1. Binary Images
– output of the function is either the brightest pixel 1(255) or the darkest pixel 0
2. Gray Scale Images
– the output of the function is a range of possible values from the brightest
pixel 255 to the darkest pixel 0
3. Color Images
– vector valued function represent red, blue and green pixel values range 0-
255.

11. HISTOGRAM
• Histogram of image describe the intensity value of pixels that occur in an image.
• It is a plot that shows the frequency of occurrence of an event.
Image Histogram

12. Noise in images
• Image noise is random variation of brightness or color information in the
captured images.
• It is degradation in image signal caused by external sources.
• Images containing multiplicative noise have the characteristic that brighter the
area the noisier it. But mostly it is additive.

13. Noise in images
• Model a noisy image as
g(x, y) = f(x, y) + η(x, y)
g(x, y)= function of noisy image, η(x, y) = function of image noise ,
f(x, y) = function of original image.
Sources of Image noise:
• While image being sent electronically from one place to another through satellite,
wireless, etc
• Sensor heat while clicking an image.
• With varying ISO Factor which varies with the capacity of camera to absorb light.
h(x, y) = Spatial representation of H.
Convolution in Spatial domain = multiplication
in Frequency Domain

14. Types of Image Noise
1. Salt and pepper noise / Impulse noise/ Shot noise / Spike noise
• contains random occurrences of black or white or both pixels
• Probabilities Density Function (PDF), p(z) is distribution salt and pepper
noise in image
• Reasons for impulse noise:
– memory cell failure.
– malfunctioning of camera’s sensor cells.
– synchronization errors in image digitizing or transmission
• Filtering techniques for impulse noise
• Mean filtering
• Median filtering
• Gaussian filtering





=
=
=
otherwise
0
for
for
)
( b
z
P
a
z
P
z
p b
a

15. Types of Image Noise
2. Gaussian noise:
• variations (fluctuation) in intensity drawn from a Gaussian normal
distribution
• This noise contains pdf of the normal distribution
Z – random variable
Sources of Gaussian Noise
• It occurs during acquisition
o E.g. Sensor noise caused by poor illumination and/or high
temperature
• Transmission
o e.g. Electronic circuit noise .
Gaussian Noise filtering techniques
• Mean (convolution) filtering
• Median filtering
• Gaussian filtering Original
Image
Noisy Image
2
2
2
/
)
(
2
1
)
( 



−
−
= z
e
z
p

16. Types of Image Noise
3. Speckle Noise
• Speckle noise can be modeled by random values multiplied by
pixel values of an image
• Output from random fluctuations in the return signal from an
object is not bigger than a single image-processing element.
• It increases the mean grey level of a local area.
• The distribution noise can be expressed as g(n, m), is the observed
image, u(n, m) is the multiplicative component . and (n, m) is the
additive component of the speckle noise.
Speckle Noise filtering techniques
• Mean (convolution) filtering
• Median filtering
Original
Image
Noisy Image

17. Types of Image Noise
4. Uniform Noise
• The uniform noise cause by quantizing the pixels of image to a
number of distinct levels is known as quantization noise.
• Uniform noise can be analytically described by the gray level
values of the noise that are evenly (uniformly) distributed across a
specific range.
• Quantization noise has an approximately uniform distribution
Original
Image
Noisy Image







−
=
otherwise
0
if
1
)
(
b
z
a
a
b
z
p
2
b
a +
=

12
)
( 2
2 a
b −
=


18. Special Types of Image Noise
5. Rayleigh noise
Radar range and velocity images typically contain noise that
can be modeled by the Rayleigh distribution.
6. Erlang (Gamma) noise
It is a two-parameters positive integer for shape, positive real
number for rate of continuous probability distributions.
7. Exponential noise (Special Case of Gamma Noise)
Continuous probability distributions. It is used to model the
time elapsed between events

19. Noise Removal
• Use spatial filters to remove different kinds of noise.
• Noise reduction can be implemented in spatial and frequency domain.
• Techniques to reduce noise are:
• Uniform Filter / Averaging Filter
• Median Filter / Order statistic Filter
• Gaussian Filter / Band Reject Filter
• Inverse Filtering
• Weiner Filtering
• A general technique to noise reduction is smoothing and median filter.

20. Average / Mean / Uniform filter
• Spatial filter removes impulse noise (salt and pepper noise).
• The averaging filter of size 3x3 pixels is:
• m, n are no. of rows and no. of columns.
• g(s, t) is observed noisy image.
Filter mask

21. Average / Mean filter types
Mean Filter
Harmonic
(Arithmetic) Mean
Geometric Mean
Contraharmonic
Mean
• Arithmetic and geometric mean filters are suitable for Gaussian or uniform noise
• Contraharmonic filters are suitable for impulse noise

22. Harmonic Mean Filter
• Harmonic mean technique reduces the salt noise.
• But, it can’t reduce pepper noise well.
• This technique also can reduce damaged image due to Gaussian noise.
Geometric Mean Filter
• The result obtained from geometric mean produces blur image.
• The information of image will lost.

23. Contraharmonic Mean Filter
• Q is the order of the filter and adjusting its value changes the
filter’s behaviour.
• if the Q value is negative value, it can reduce salt noise.
• if the Q value is positive value, it can reduce pepper noise.
• This technique can’t eliminate both salt and pepper noise
concurrently.

24. Order Statistics Filters
• Spatial filters that are based on ordering the pixel values that make
up the neighbourhood operated on by the filter
• Spatial filters are
– Median filter
– Max and min filter
– Midpoint filter
– Alpha trimmed mean filter

25. Median Filter
• Median filter technique reduces impulse noise such as Salt and Pepper
well.
• Median filter is defined as:
• Center (median) value in the original image 3x3 pixels is replaced by
the median value.
• Median filter technique is applied for each non-overlapping block of 3x3
pixels, from top-left corner to top-right corner and from top to bottom.

26. Median Filter
164 156 145 96 168 188
146 135 90 185 200 198
137 83 189 199 214 199
94 191 215 211 201 198
179 221 200 218 222 201
185 210 221 220 198 214
164 156 145 96 168 188
146 135 90 185 200 198
137 83 191 199 214 199
94 189 215 211 201 198
179 221 200 218 222 201
185 210 221 220 198 214
ascending order : 83, 94, 137, 179, 189, 191, 200, 215, 221
• The 2 D array shows the grayscale image with 3x3 filter.
• Pixel intensity value 191 replaced by 3 x 3 filter median intensity value
189.

27. Median Filter
The computational
block overlap only
pixels that are in the
original image.
The computational block
overlap pixels outside
the original image, but
the center pixel overlaps
a pixel in the image.
The computational
block overlap pixels at
the edges only. The
center pixel is outside
the image.

28. Adaptive median Filters
• Adaptive median filters can perform better than media filter on impulse noise
such as pepper and salt noise.
• The results obtained from adaptive median filter produce slightly smooth image.
• The behaviour of adaptive filters changes depending on the characteristics of the
image inside the filter region.
• The median filter performs relatively well on impulse noise as long as the spatial
density of the impulse noise is not large.
• The adaptive median filter can handle much more spatially dense impulse noise,
and also performs some smoothing for non-impulse noise.
• The key insight in the adaptive median filter is that the filter size changes
depending on the characteristics of the image.
• Filtering looks at each original pixel image and generates a new filtered pixel.

29. Adaptive median Filters
– zmin = minimum grey level in Sxy
– zmax = maximum grey level in Sxy
– zmed = median of grey levels in Sxy
– zxy = grey level at coordinates (x, y)
– Smax = maximum allowed size of Sxy
Level A: A1 = zmed – zmin
A2 = zmed – zmax
if A1 > 0 and A2 < 0, Go to level B
else increase the window size
if window size ≤ repeat Smax level A
else output zmed
Level B: B1 = zxy – zmin
B2 = zxy – zmax
if B1 > 0 and B2 < 0, output zxy
else output zmed

30. Adaptive median Filters
• Adaptive median filter has three purposes:
– Remove impulse noise
– Provide smoothing of other noise
– Reduce distortion such as excessive thinning or thickening of
object boundaries

31. Max and Min Filter
Max Filter:
Min Filter:
• Max filter is good for pepper noise and min is good for salt
noise
)}
,
(
{
max
)
,
(
ˆ
)
,
(
t
s
g
y
x
f
xy
S
t
s 
=
)}
,
(
{
min
)
,
(
ˆ
)
,
(
t
s
g
y
x
f
xy
S
t
s 
=

32. Midpoint Filter
• Good for random Gaussian and uniform noise





 +
=


)}
,
(
{
min
)}
,
(
{
max
2
1
)
,
(
ˆ
)
,
(
)
,
(
t
s
g
t
s
g
y
x
f
xy
xy S
t
s
S
t
s
Alpha-Trimmed Mean Filter:
• Hybrid of median and mean filters
• Work on the monochrome images only 8 bit and 24 bits.
• Alpha parameter is d responsible for number of trimmed (discard) element
• Average the pixel values by Delete the d/2 lowest and d/2 highest grey level
values. So use the remaining mn – d pixels.
• Useful in situations involving multiple types of noise, such as a combination of
salt-and-pepper and Gaussian noise


−
=
xy
S
t
s
r t
s
g
d
mn
y
x
f
)
,
(
)
,
(
1
)
,
(
ˆ

33. Periodic Noise
• Periodic noise arises due to
electrical or electromagnetic
interference.
• Gives rise to regular noise
patterns in an image
• Frequency domain techniques in the
Fourier domain are most effective at
removing periodic noise.
• Frequency domain data range from 0 to
2π.

34. Gaussian Filter / Gaussian Smoothing Filter
• Gaussian filtering is used to blur images and remove noise using Gaussian
function.
• Blurring is used in preprocessing steps, such as removal of small details
from an image prior to object extraction, and bridging of small gaps in
lines or curves.
• Noise reduction can be accomplished by blurring
• In edge detection, Gaussian smoothing is done prior to Laplacian to
remove the effect of noise.
• σ - variance of the mask (filter)
• Gaussian filters design can be controlled by manipulating just one
variable- the variance.

35. Gaussian Filter / Gaussian Smoothing Filter
• The value of the variance corresponds inversely to the amount of filtering,
smaller values of sigma has more frequencies are suppressed and vice
versa.
• The Standard deviation plays major role in its behavior.
• The values located between +/- of σ for 68%, while two standard deviations
from the mean (blue and brown) account for 95%, and three standard deviations
(blue, brown and green) for 99.7%.
• This is very important when designing a Gaussian kernel of fixed length.

36. Band Reject Filters
• Removing periodic noise form an image involves removing a
particular range of frequencies from that image.
• Distance function - Band reject filters uses distance of each
element of the transfer function to the origin (0,0).
• An ideal band reject filter is









+

+


−
−

=
2
)
,
(
1
2
)
,
(
2
0
2
)
,
(
1
)
,
(
0
0
0
0
W
D
v
u
D
if
W
D
v
u
D
W
D
if
W
D
v
u
D
if
v
u
H
D(u,v) - Distance to the origin
D0 – Cutoff frequency i.e. Transition point between the pass and stop
bands of the filter
W – Band width

37. Band Reject Filters
– Butterworth band reject filter of order n determines the steepness
of the transition between the pass-band and stop-band.
• Better results can be achieved with a Gaussian shaped filter function.
• A commonly used discrete approximation to the Gaussian is the
Butterworth filter.
• Applying this filter in the frequency domain shows a similar result to the
Gaussian smoothing in the spatial domain.
n
D
v
u
D
W
v
u
D
v
u
H
2
2
0
2
)
,
(
)
,
(
1
1
)
,
(








−
+
=

38. Band Reject Filters
• The ideal band reject filter is shown along with Butterworth and
Gaussian versions of the filter.
Ideal
Band Reject Filter
Butterworth
Band Reject Filter (of order 1)
Gaussian
Band Reject Filter

39. Inverse filter
• Compute an estimate F’( u, v) of the transform of the original image by:
• 𝐹′ 𝑢, 𝑣 =
𝐺(𝑢,𝑣)
𝐻(𝑢,𝑣)
• Divisions are made between individual elements of the functions.
• 𝐹′ 𝑢, 𝑣 = 𝐹 𝑢, 𝑣 +
𝑁(𝑢,𝑣)
𝐻(𝑢,𝑣)
• Equation shows that even if we know degradation function, we can not
recover the undegraded image [Inverse Fourier Transform of F(u, v)]
exactly, because N(u, v) is random function whose Fourier Transform is
not known.
• If degradation has ZERO or less value then N(u, v) / H(u, v) dominates
the estimated F’(u, v).
• No explicit provision for handling Noise.

40. Maximum Mean Square Error (Wiener) Filtering
• Incorporates both degradation function and statistical characteristics of
noise into restoration process.
• Considers images and noise as random process.
• Find an estimate f’ of the uncorrupted image f such that mean square
error between them is minimized. Error measure is given by:
𝑒2 = 𝐸{ 𝑓 − 𝑓′ 2}
• E{.} = Expected value of the argument
• Assumptions:
• image and noise are uncorrelated.
• One or other has Zero mean
• Gray levels in the estimate are a linear function of levels in the
degraded image.

41. Maximum Mean Square Error (Wiener) Filtering
Based on these conditions:
• F’(u,v) =[1/H(u,v)] [ |H(u,v|2 / (|H(u,v|2 +S(u,v)/Sf(u,v))] G(u,v)
• H(u,v) – degraded function
• H * (u,v) – complecx conjugate of H(u,v)
• H(u,v) = H * (u,v)H(u,v)
• S(u,v) = |N(u,v)|2 power spectrum of noise
• Sf(u,v) = |F(u,v)|2 power spectrum of undegraded image

42. Relationship between a digital image and a signal
Signal
• In physical world, any quantity measurable through time over space considered
as a signal. A signal is a mathematical function, and it conveys some
information.
• A signal can be one dimensional or two dimensional or higher dimensional
signal.
• One dimensional signal is a signal that is measured over time. E.g. voice signal.
• The two dimensional signals are those that are measured over some other
physical quantities. E.g. digital image.
Relationship
• Anything that conveys information or broadcast a message in physical world
between two observers is a signal.
• When human speak, voice is converted to a sound wave/signal and transformed
with respect to the time to opponent person.
• Also, acquiring an image from a digital camera involves transfer of a signal from
one part of the system to the other.

43. References
• Richard Szeliski, Computer Vision: Algorithms and Applications,
Springer 2010