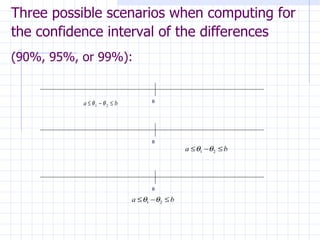
There are two main statistical techniques for comparing systems: independent sampling and correlated sampling. When comparing two systems, it is necessary to use confidence intervals. There are three possible scenarios when computing confidence intervals depending on if the sampling is independent or correlated. When comparing several designs, the goals may be to estimate each performance measure, compare to a present system, or select the best. The Bonferroni approach can be used to make statements about multiple alternatives while controlling the overall confidence level. Design of experiments tools like factorial designs, screening, and response surface methods can help understand the effect of design alternatives on performance measures.

1. Comparison and Evaluation of Alternative Designs Adapted from J. Banks

4. Three possible scenarios when computing for the confidence interval of the differences (90%, 95%, or 99%): 0 0 0