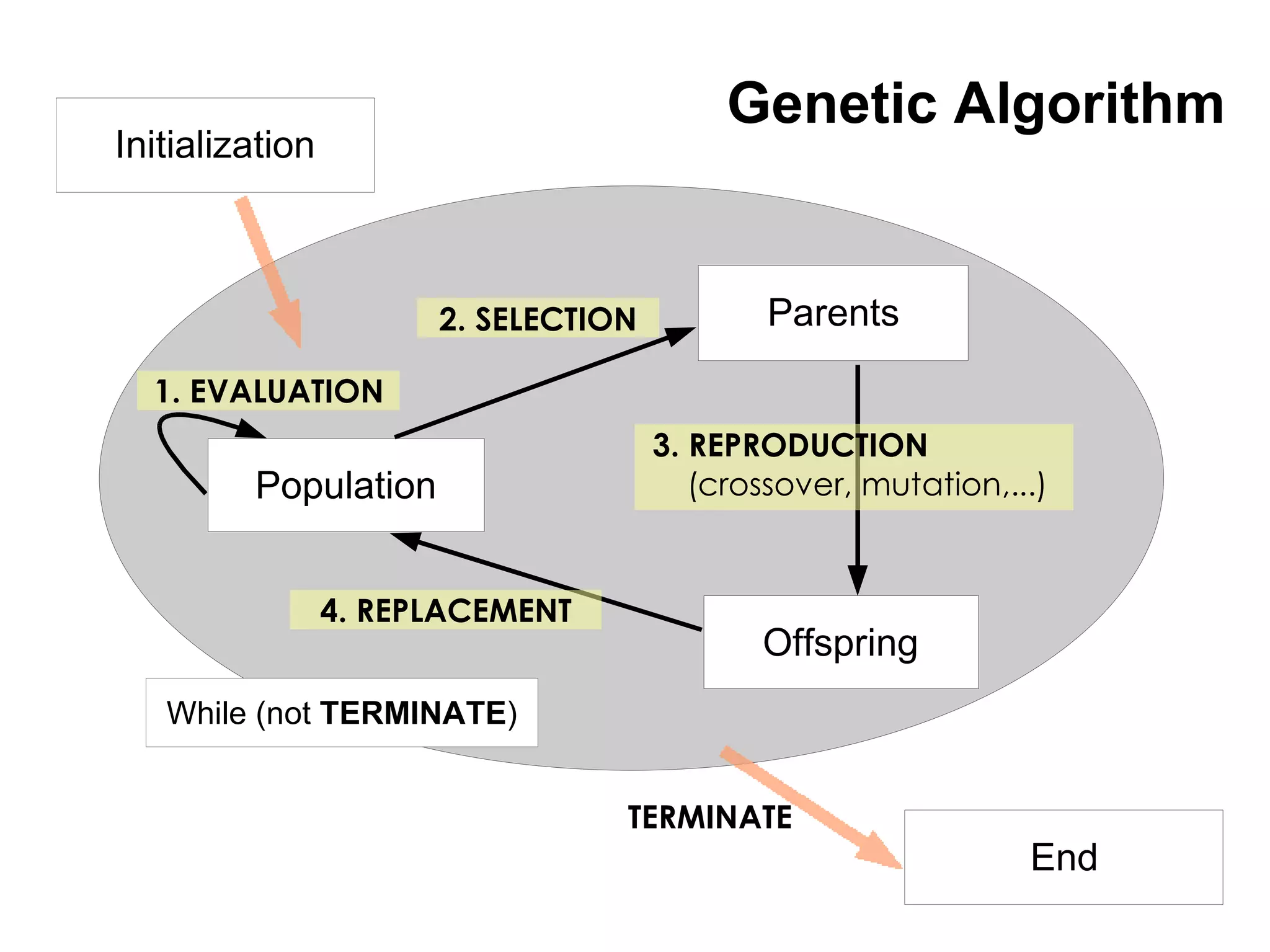
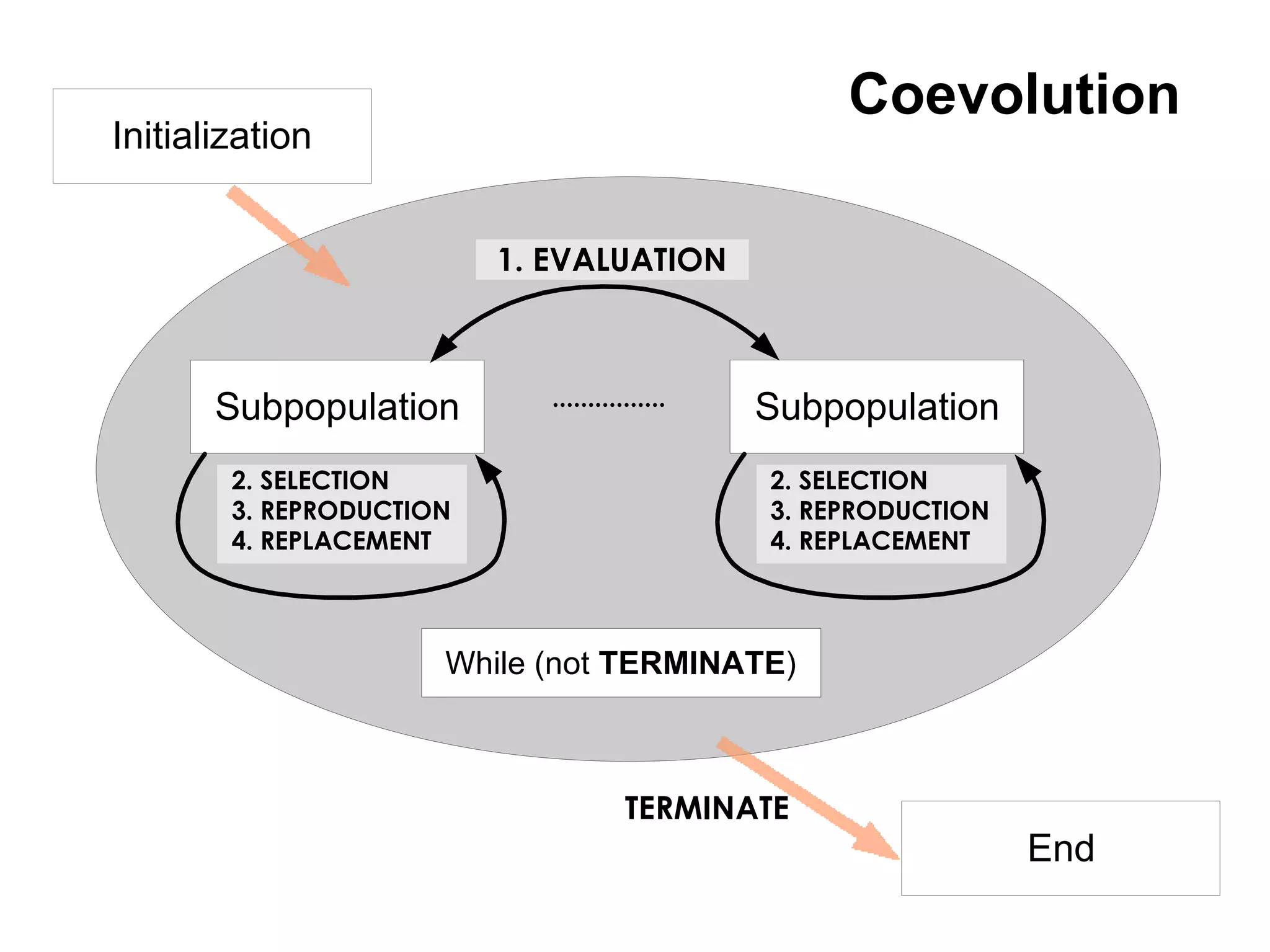
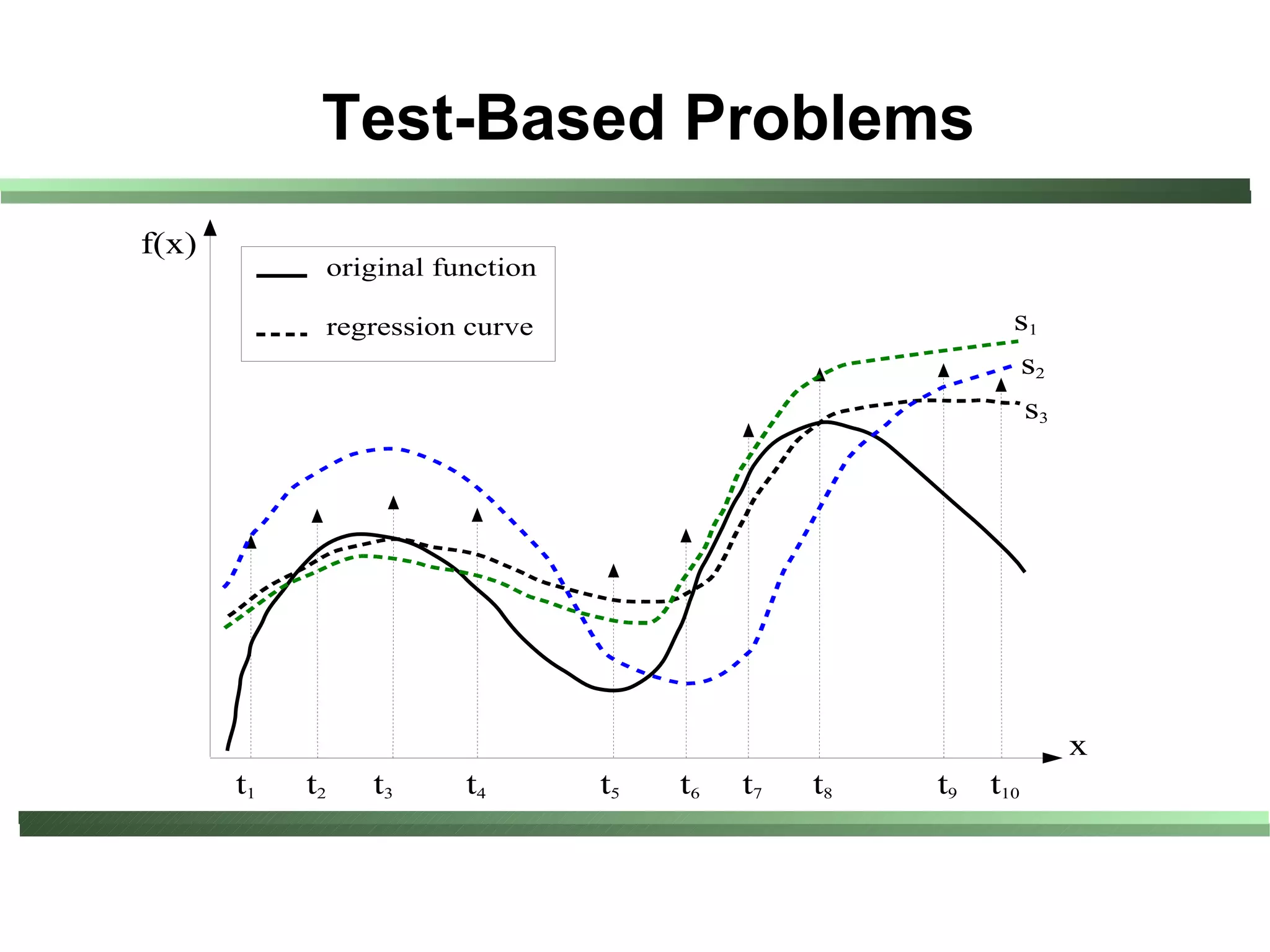
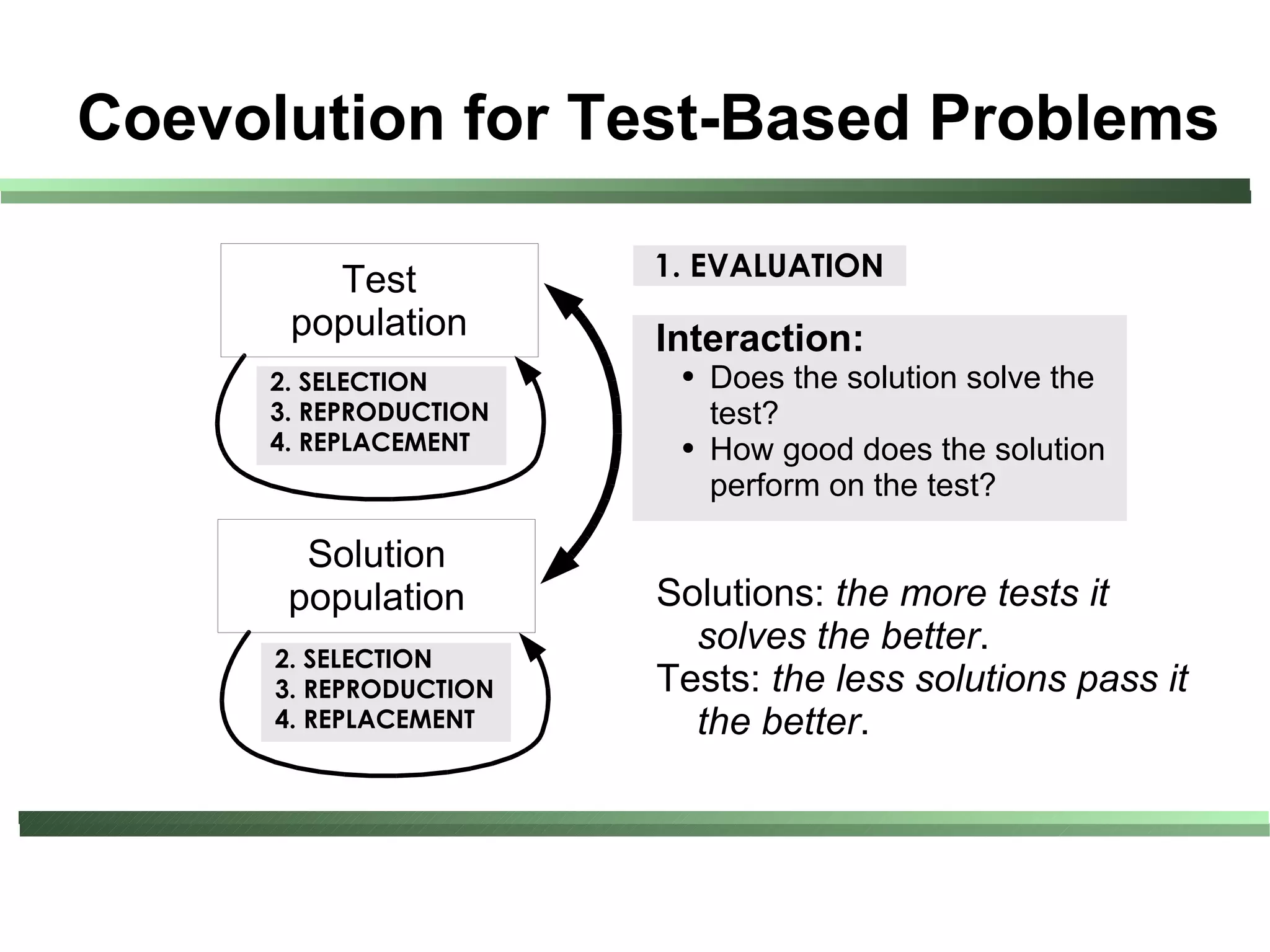
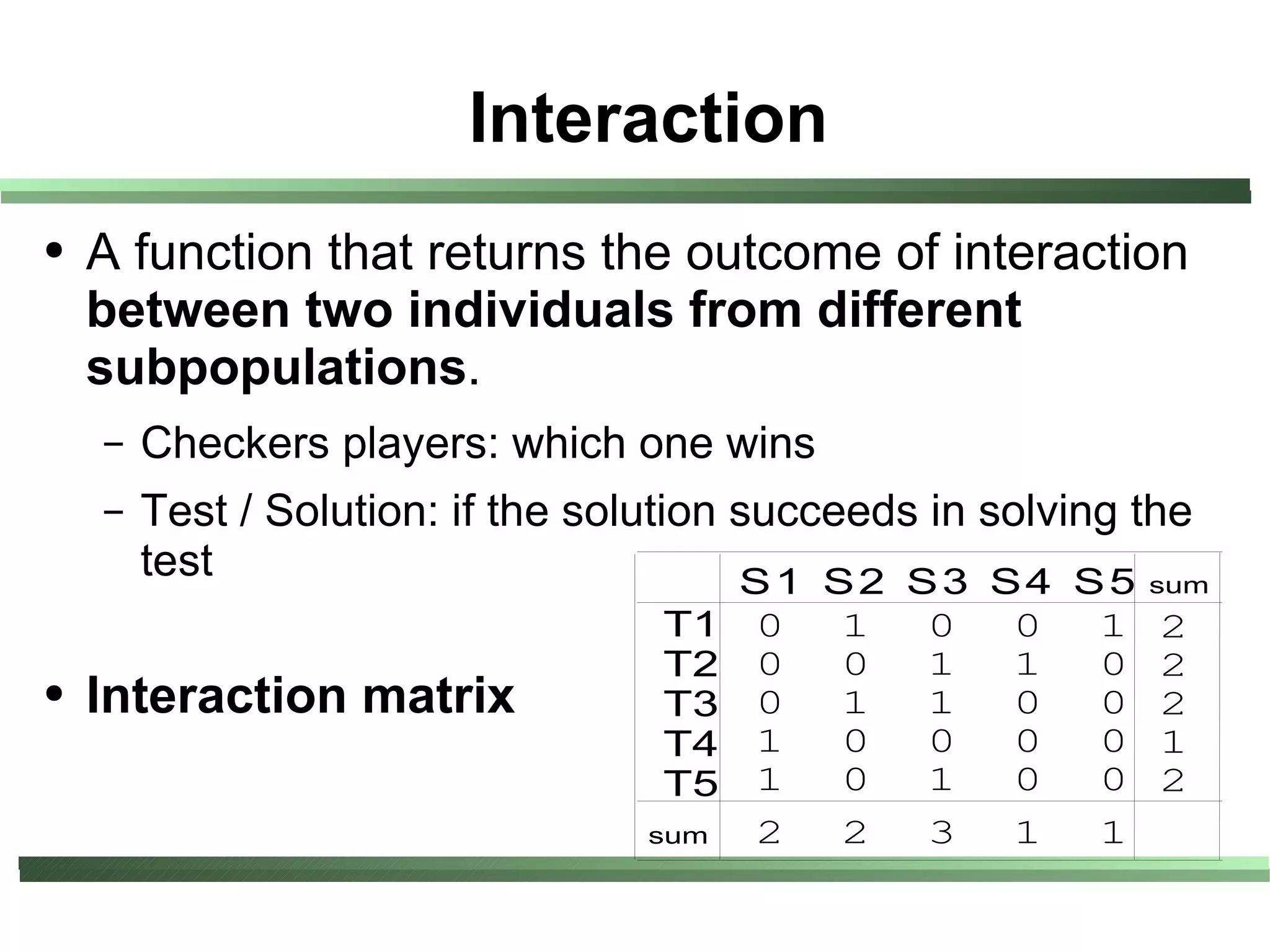
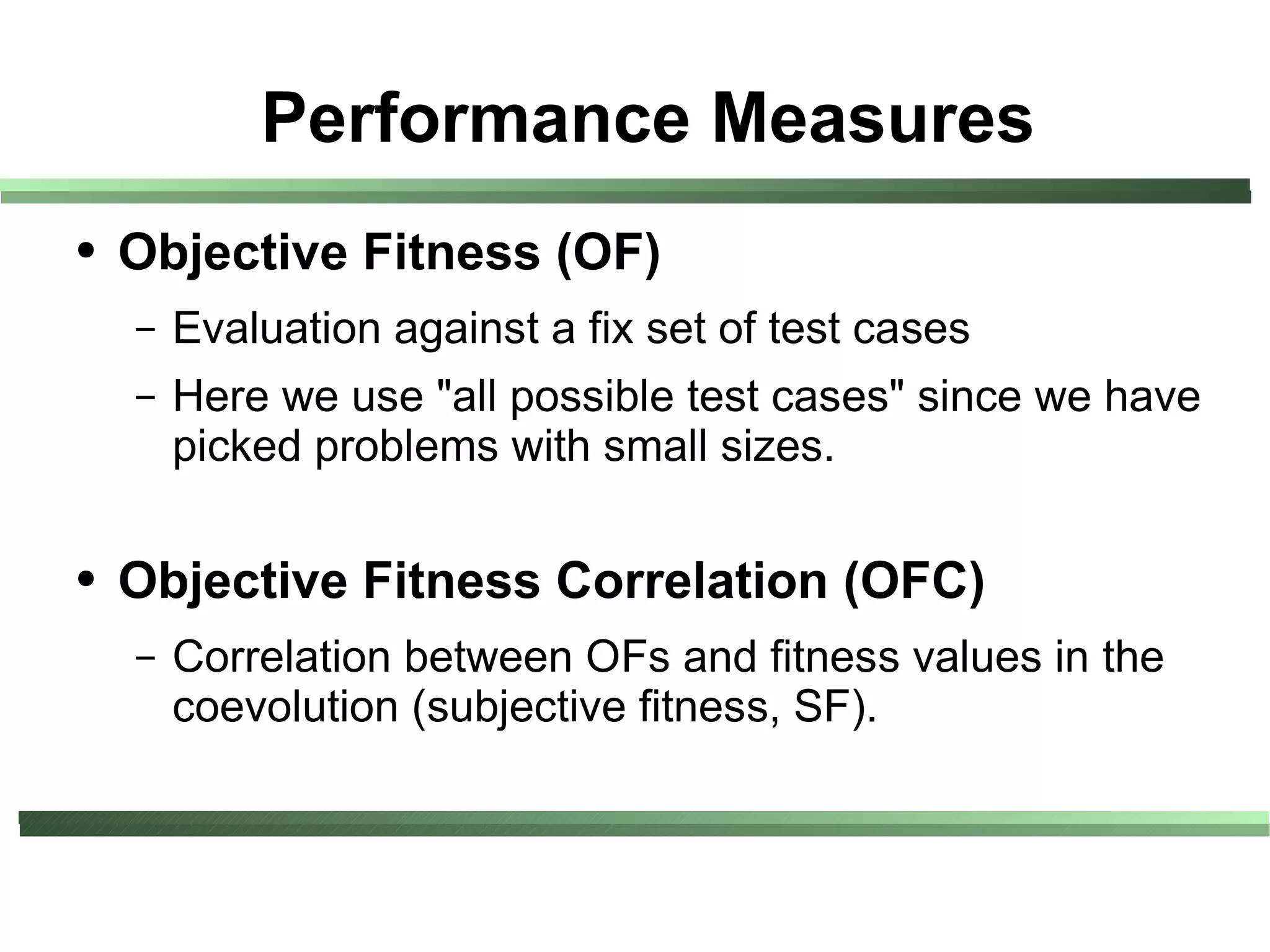
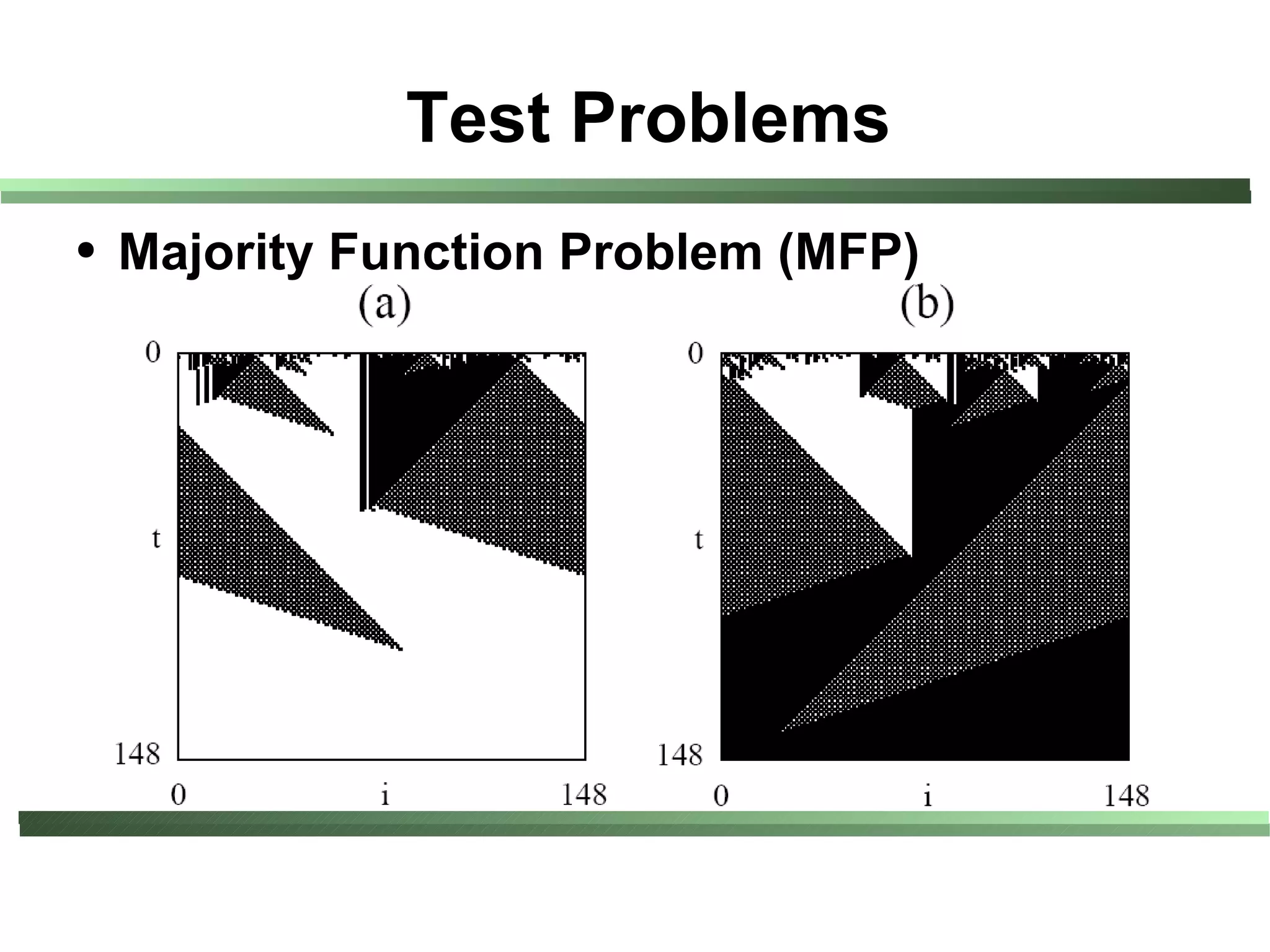
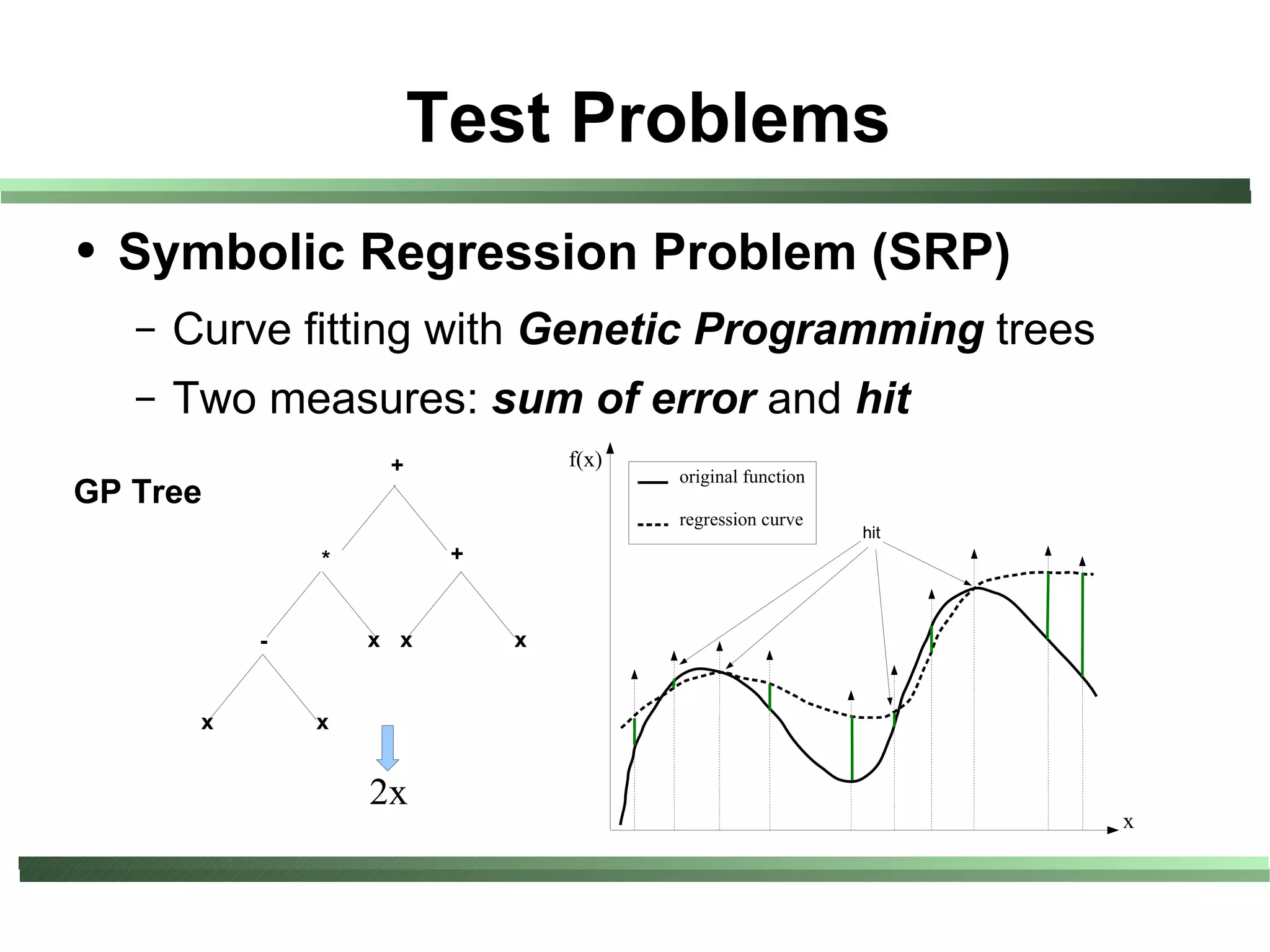
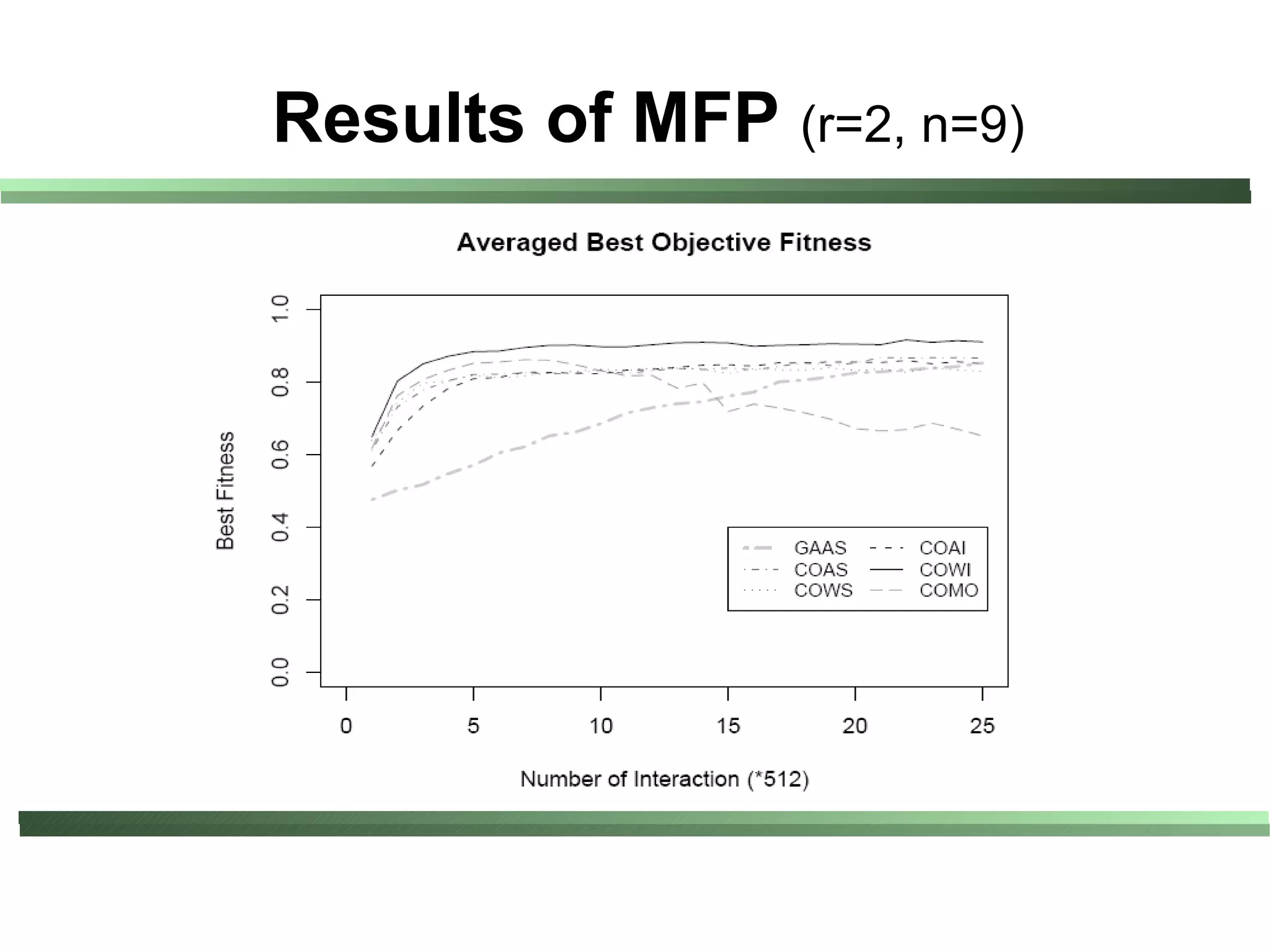
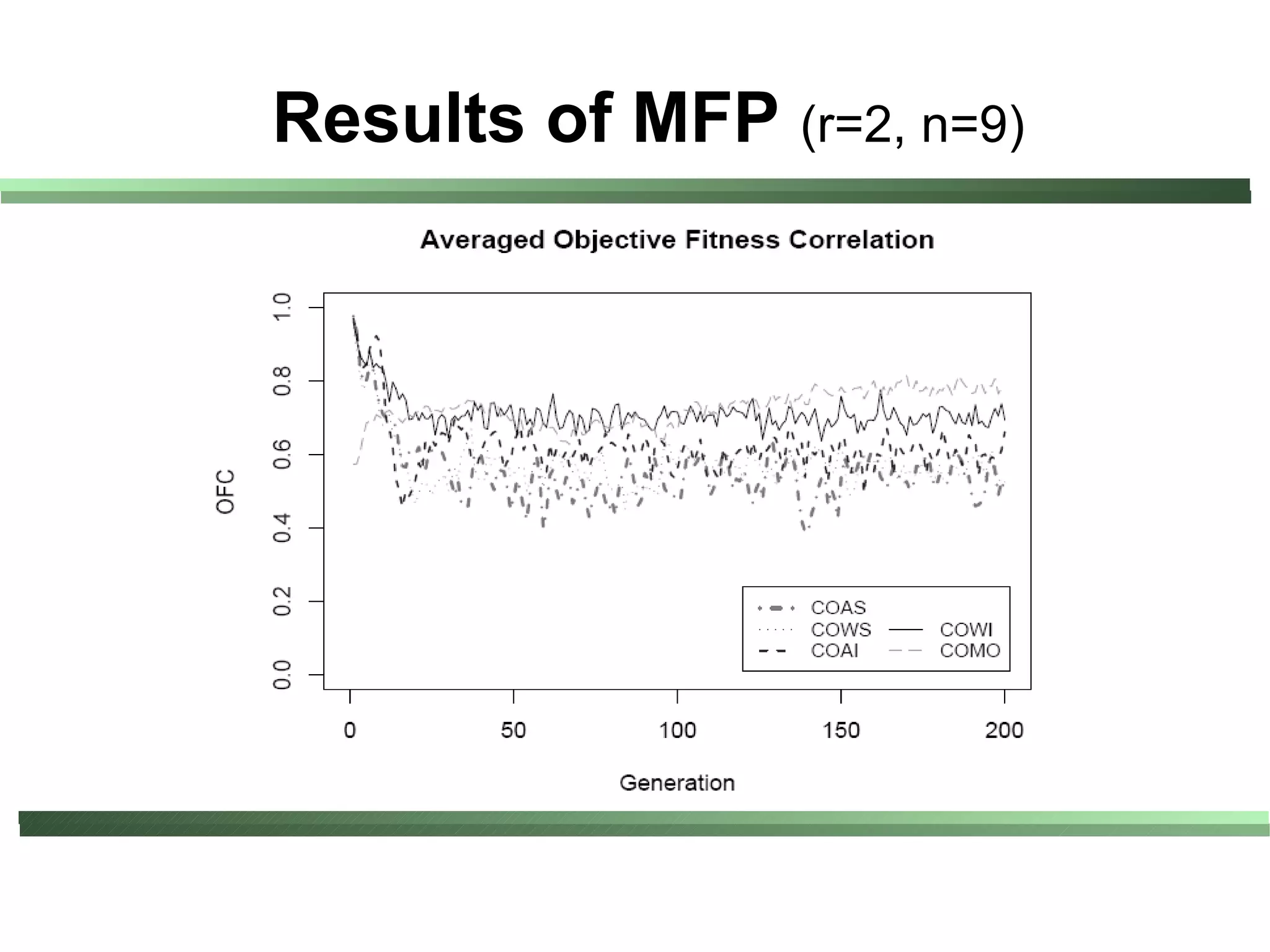
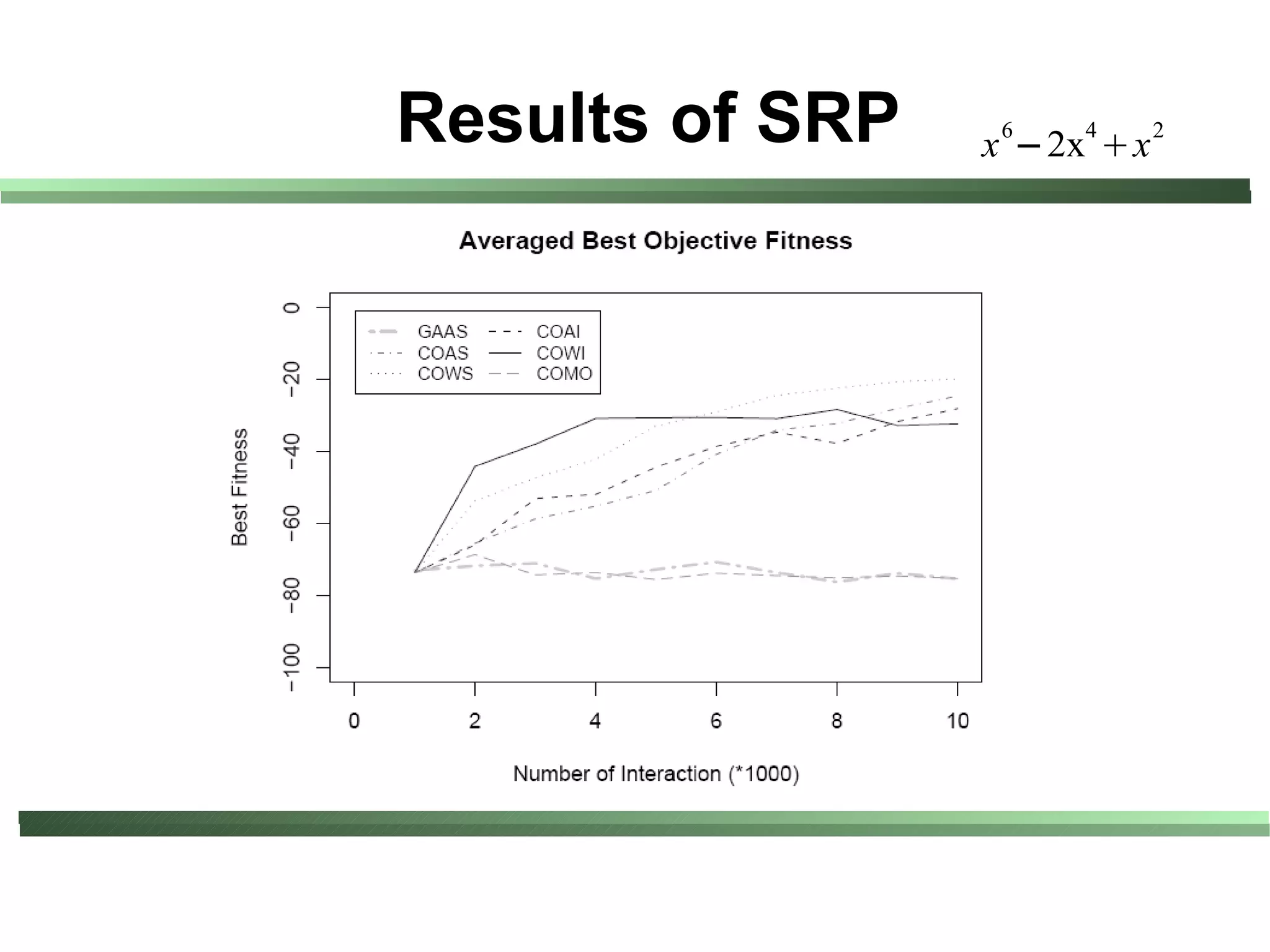
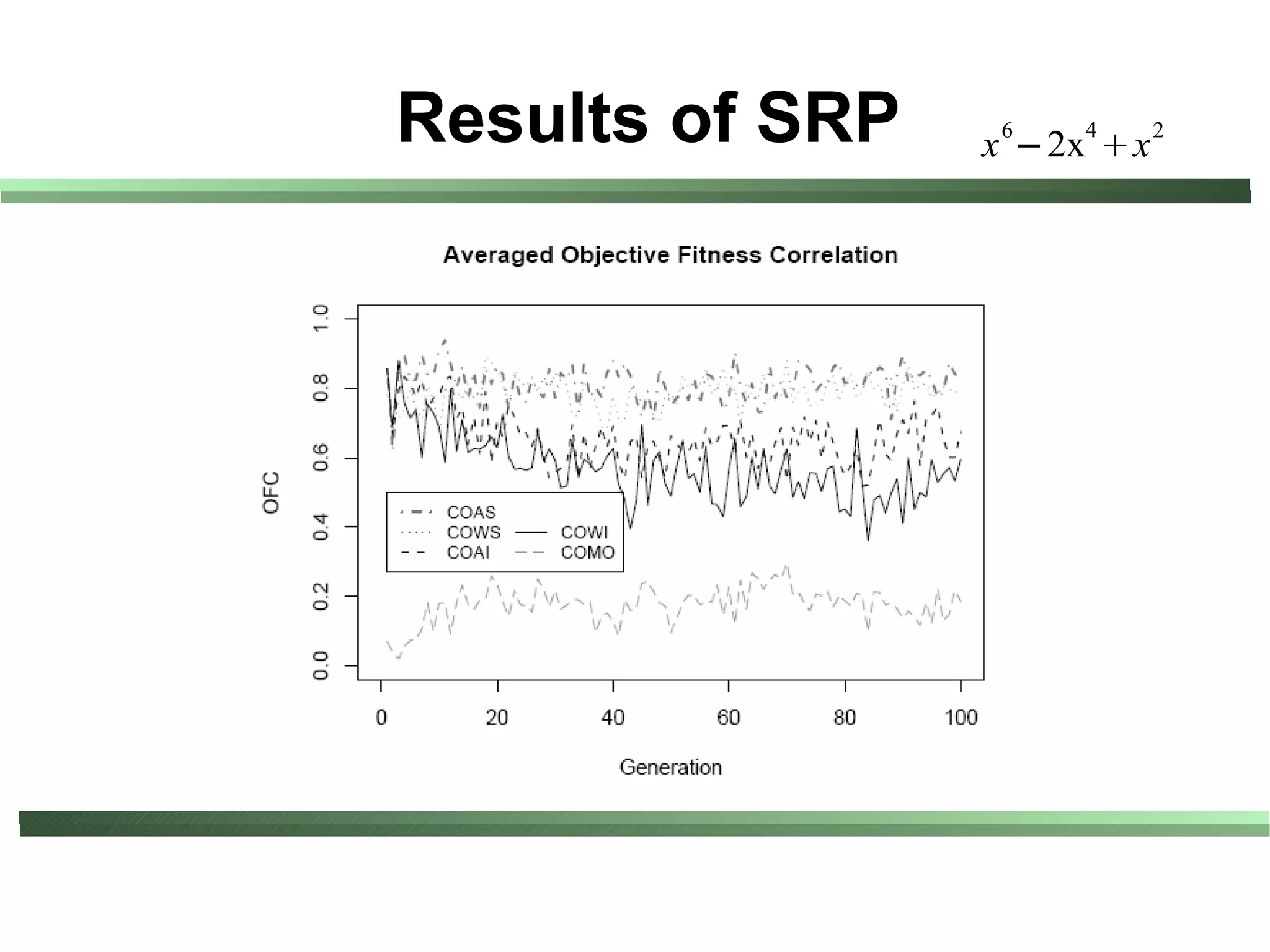
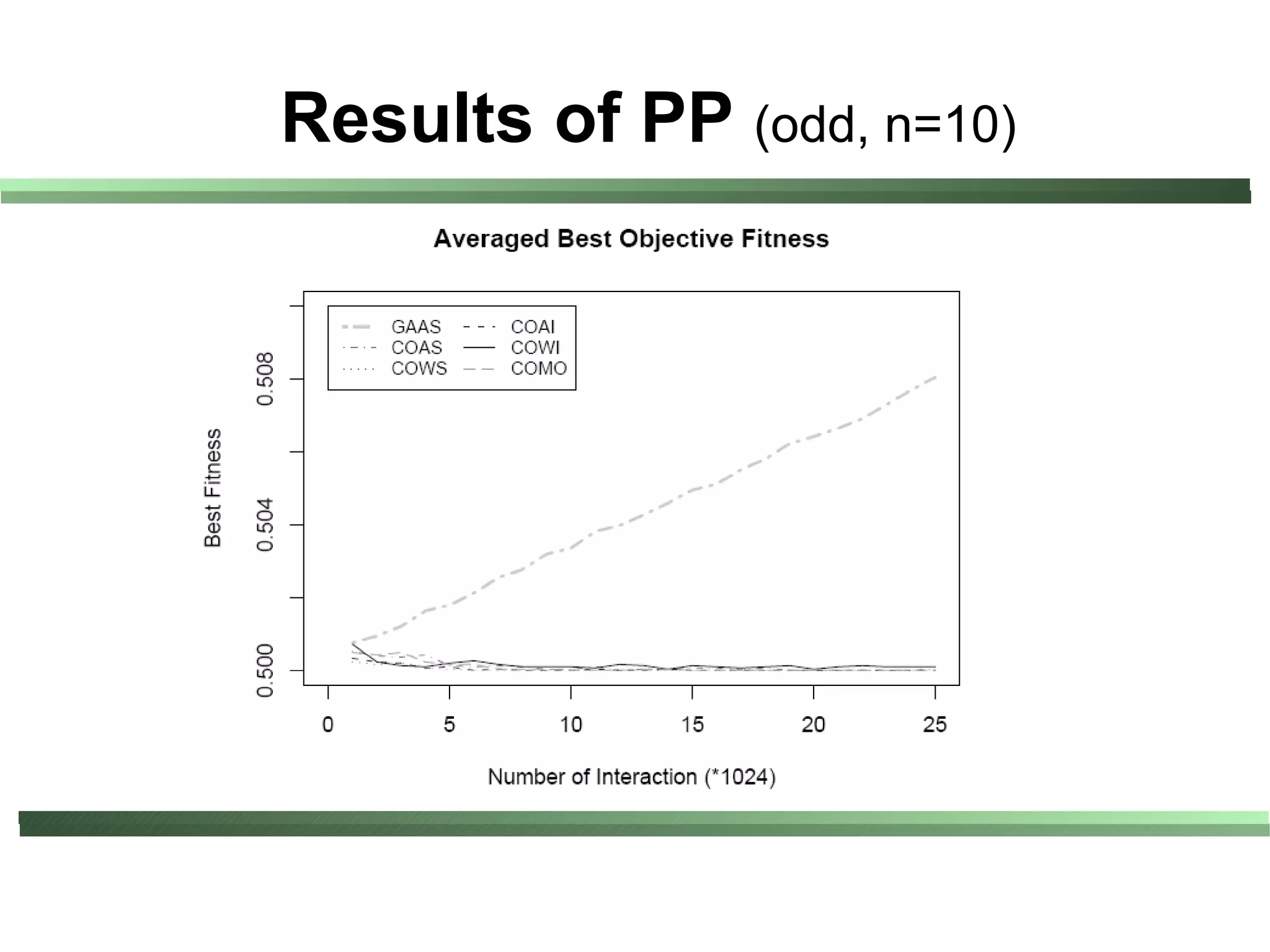
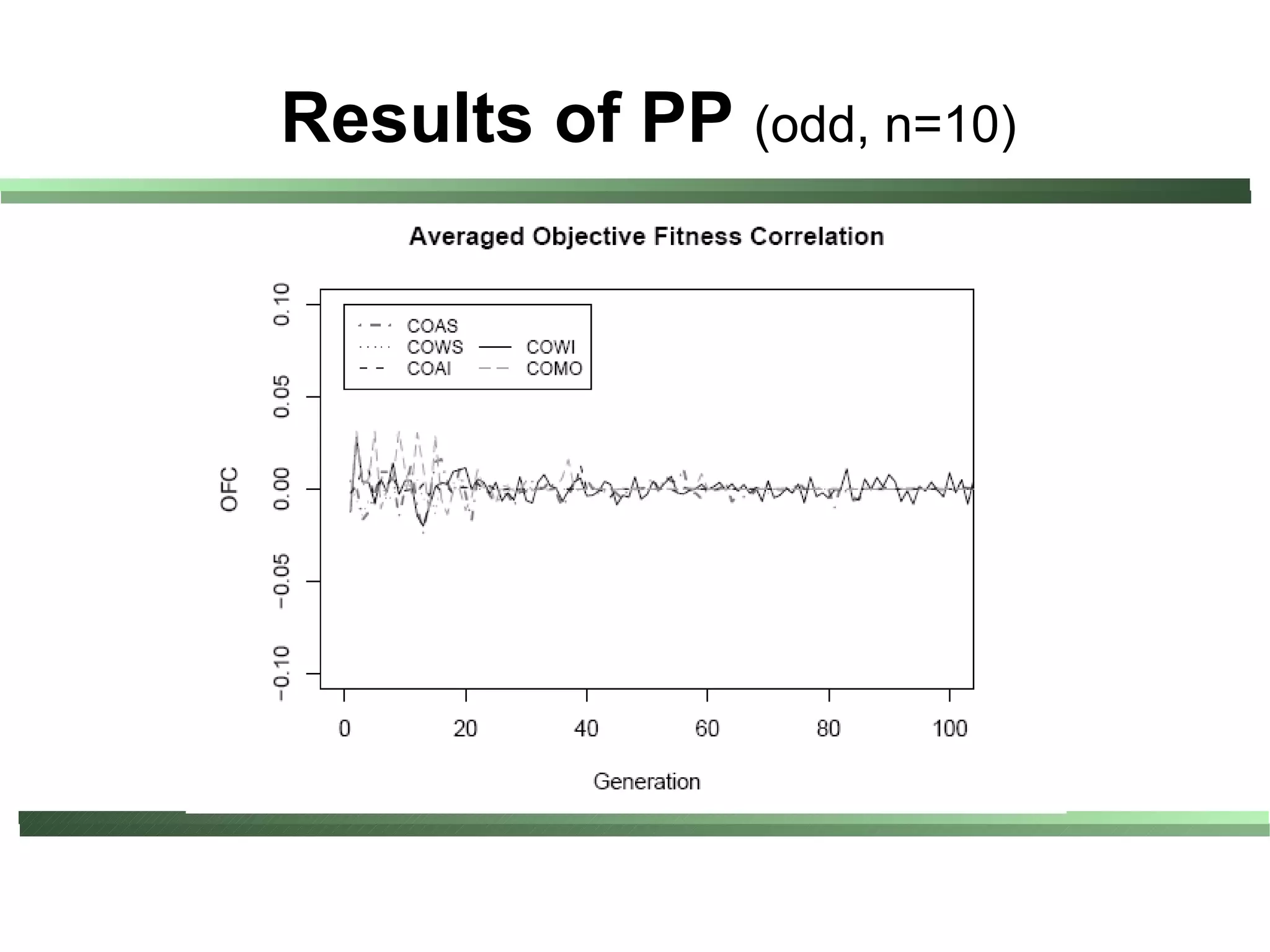
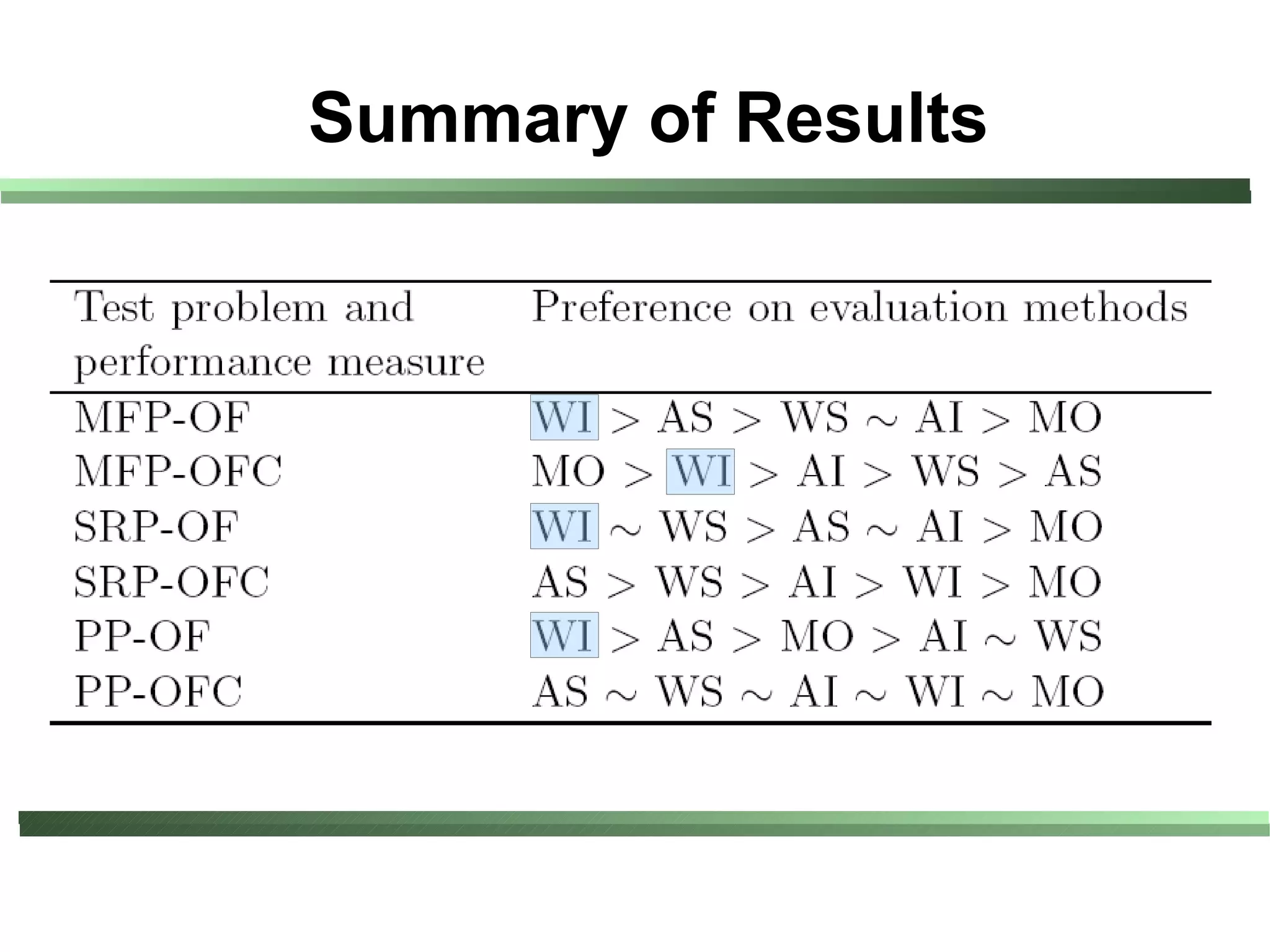
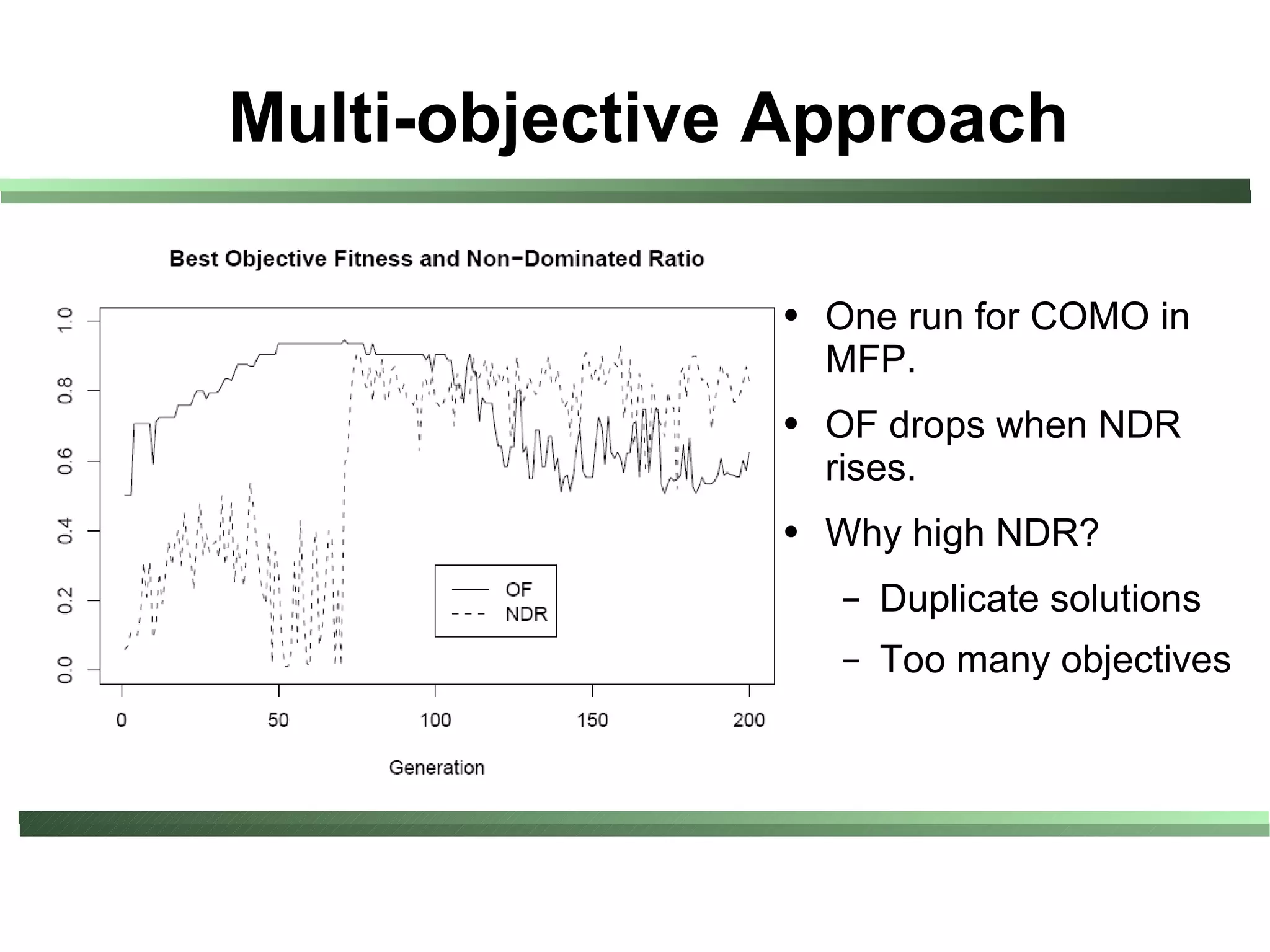
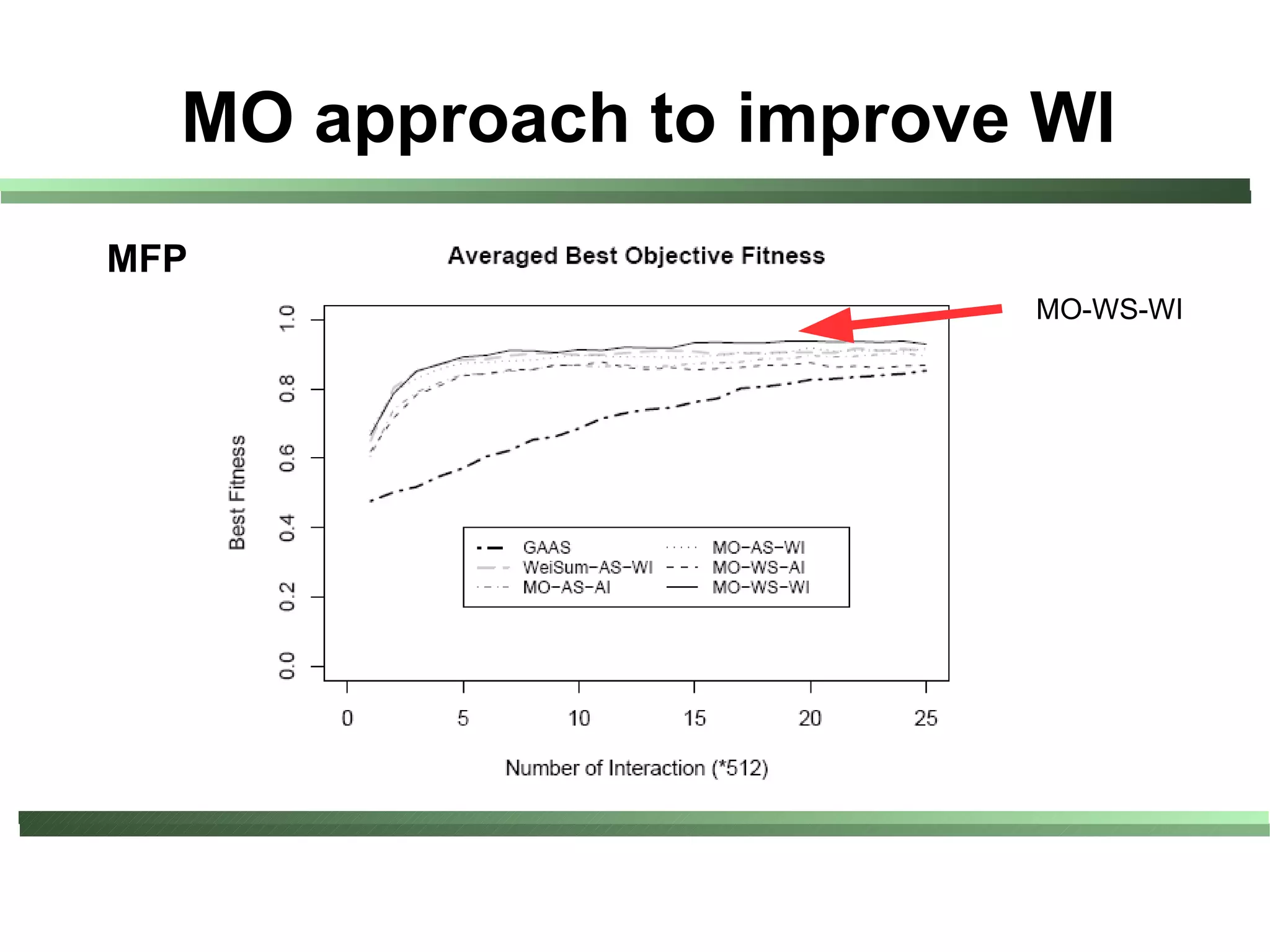
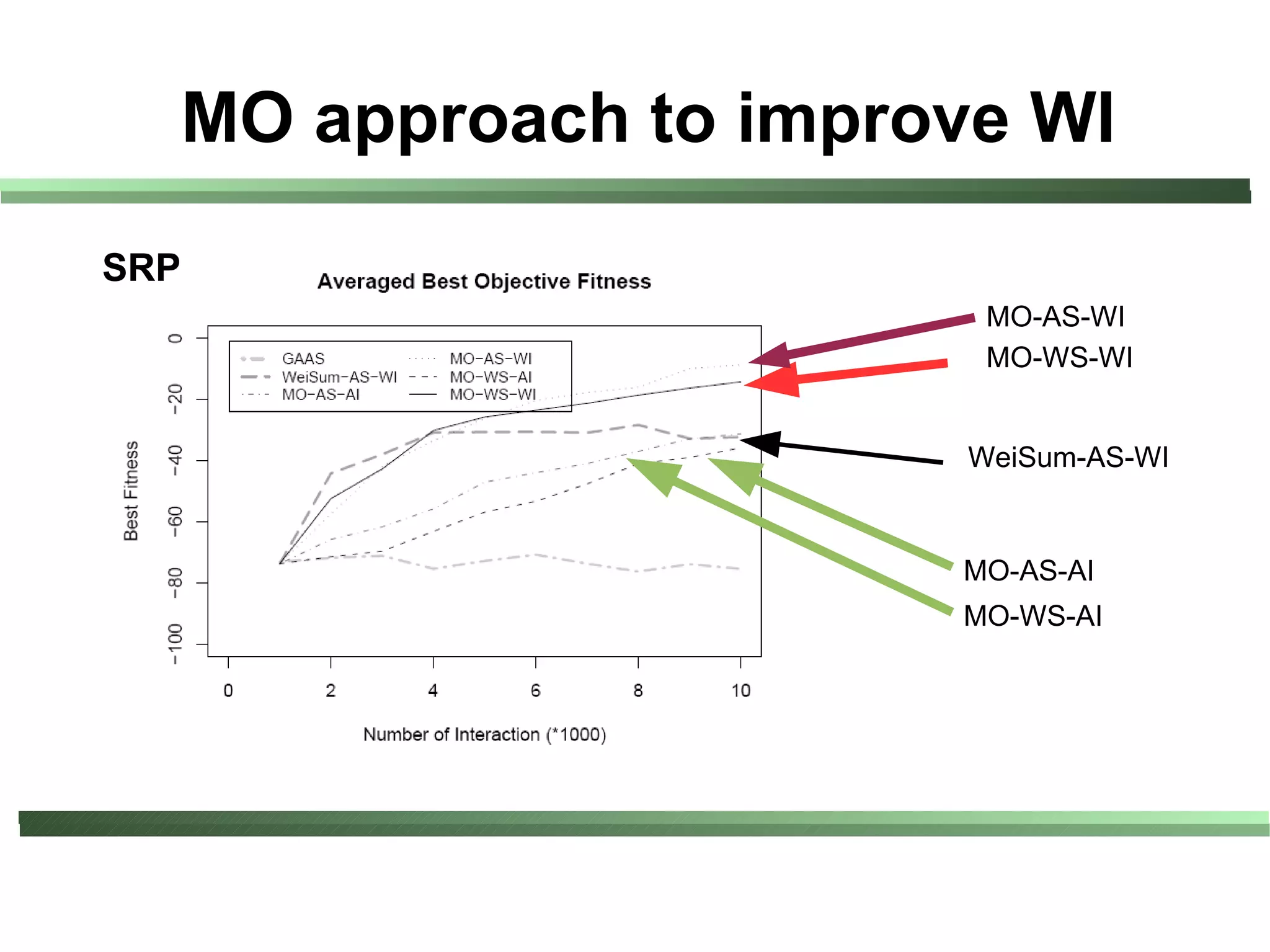
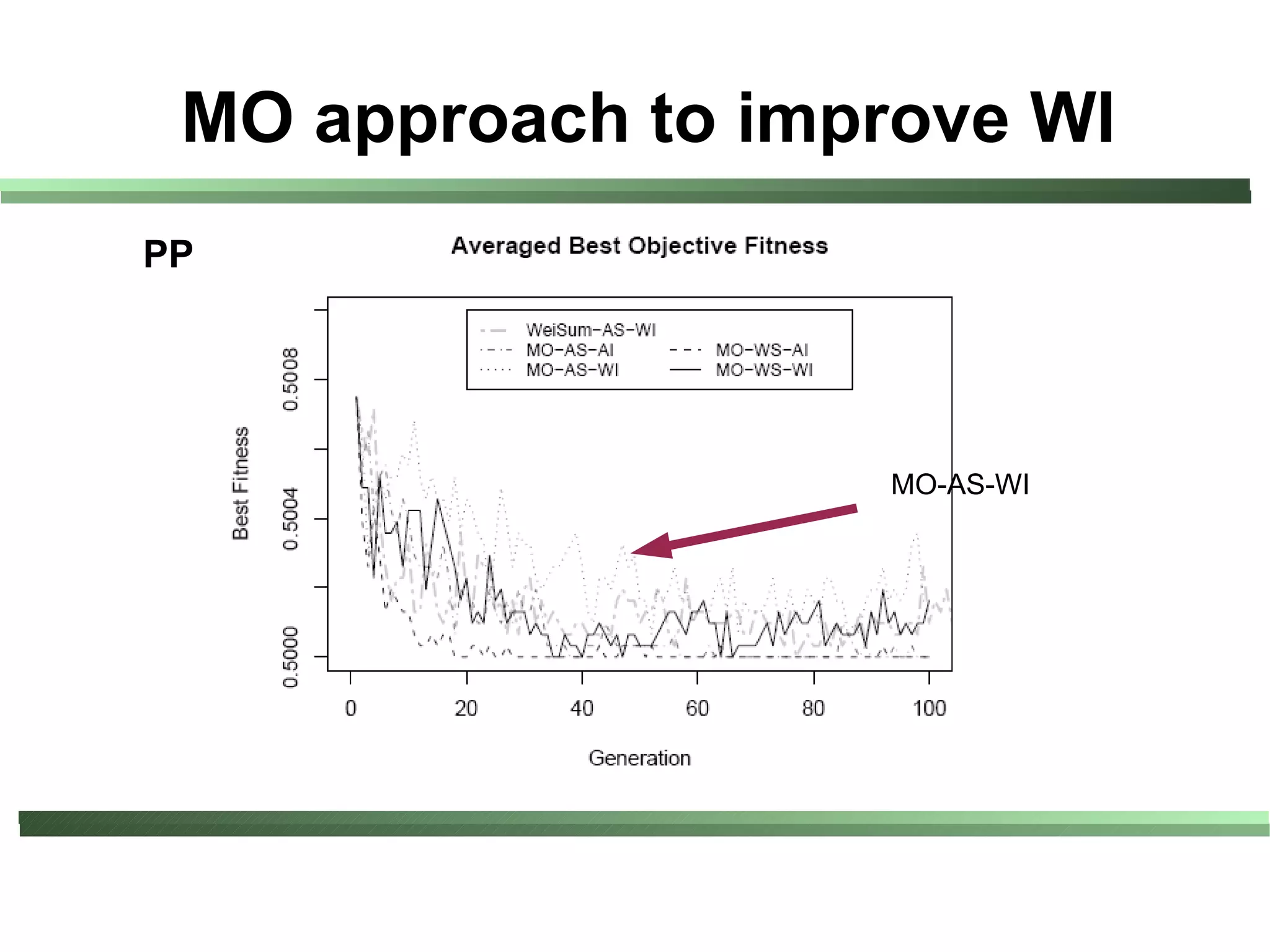
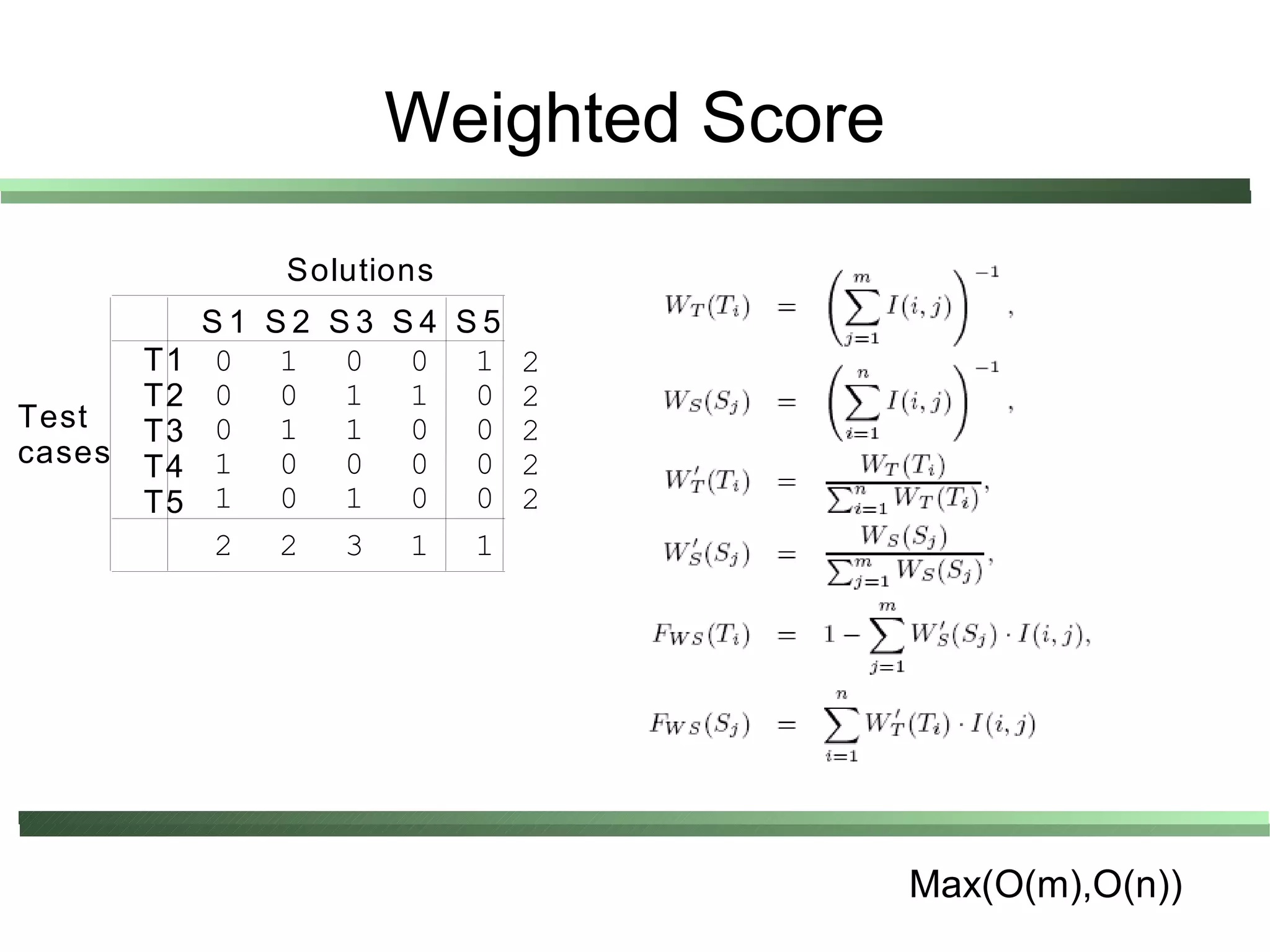
This document compares different evaluation methods in coevolution, including averaged score, weighted score, averaged informativeness, weighted informativeness, and a multi-objective approach. It presents results on three test problems: majority function problem, symbolic regression problem, and parity problem. The results show that the multi-objective approach achieves the best performance in terms of objective fitness and correlation between subjective and objective fitness.

1. Final Presentation INF/SCR-06-54
Applied Computing Science, ICS
A Comparison of Evaluation
Methods in Coevolution
Ting-Shuo Yo
Supervisor: Edwin D. de Jong
Arno P.J.M. Siebes

2. Outline
● Introduction
● Evaluation methods in coevolution
● Performance measures
● Test problems
● Results and discussion
● Concluding remarks

3. Introduction
● Evolutionary computation
● Coevolution
● Coevolution for test-based problems
● Motivation of this study

4. Genetic Algorithm
Initialization
2. SELECTION Parents
1. EVALUATION
3. REPRODUCTION
Population (crossover, mutation,...)
4. REPLACEMENT
Offspring
While (not TERMINATE)
TERMINATE
End

5. Coevolution
Initialization
1. EVALUATION
................
Subpopulation Subpopulation
2. SELECTION 2. SELECTION
3. REPRODUCTION 3. REPRODUCTION
4. REPLACEMENT 4. REPLACEMENT
While (not TERMINATE)
TERMINATE
End

6. Test-Based Problems
f(x)
original function
regression curve s1
s2
s3
x
t1 t2 t3 t4 t5 t6 t7 t8 t9 t10

7. Coevolution for Test-Based Problems
Test 1. EVALUATION
population Interaction:
2. SELECTION ● Does the solution solve the
3. REPRODUCTION test?
4. REPLACEMENT ● How good does the solution
perform on the test?
Solution
population Solutions: the more tests it
solves the better.
2. SELECTION
3. REPRODUCTION Tests: the less solutions pass it
4. REPLACEMENT the better.

8. Motivation
● Coevolution provides a way to select tests
adaptively → stability and efficiency
● Solution concept → stability
● Efficiency depends on selection and
evaluation.
● Compared to evaluation based on all relevant
information, how do different coevolutionary
evaluation methods perform?

9. Concepts for Coevolutionary
Evaluation Methods
● Interaction
● Distinction and informativeness
● Dominance and multi-objective approach

10. Interaction
● A function that returns the outcome of interaction
between two individuals from different
subpopulations.
– Checkers players: which one wins
– Test / Solution: if the solution succeeds in solving the
test S 1 S 2 S 3 S 4 S 5 sum
T1 0 1 0 0 1 2
T2 0 0 1 1 0 2
● Interaction matrix T3 0 1 1 0 0 2
T4 1 0 0 0 0 1
T5 1 0 1 0 0 2
sum 2 2 3 1 1

11. Distinction
Solutions T3
S1 S2 S3 S4 S5 sum S1 S2 S3 S4 S5 sum
T1 0 1 0 0 1 2 S1 - 0 0 0 0
T2 0 0 1 1 0 2 S2 1 - 0 1 1
Test T3 0 1 1 0 0 2 S3 1 0 - 1 1
cases T4 1 0 0 0 0 1 S4 0 0 0 - 0
T5 1 0 1 0 0 2 S5 0 0 0 0 -
sum 2 2 3 1 1 sum 2 0 0 2 2 6
● Ability to keep diversity on the other subpopulation.
● Informativeness

12. Dominance and MO approach
f2
non-dominated
S1 is dominated by S2 iff:
dominated
f1
● Keep the best for each objective.
● MO: number of individuals that dominate it

13. Evaluation Methods
● AS: Averaged Score
● WS: Weighted Score
● AI: Averaged Informativeness
● WI: Weighted Informativeness
● MO

14. AS and WS
● AS : (# positive interaction) / (# all interaction)
Solutions
S1 S2 S3 S4 S5 sum
T1 0 1 0 0 1 2 0.4
T2 0 0 1 1 0 2 0.4
Test T3 0 1 1 0 0 2 0.4
cases T4 1 0 0 0 0 1 0.2
T5 1 0 1 0 0 2 0.4
sum 2 2 3 1 1
0.4 0.4 0.6 0.2 0.2
● WS : each interaction is weighted differently.

15. AI and WI
● AI : # of distinctions it makes
● WI : each distinction is weighted differently.
S1>S2 S1>S3 S1>S4 S1>S5 .............
T1 1 1 0 1 .... 5
T2 0 0 0 1 .... 2
T3 1 1 0 0 .... 6
T4 0 1 0 1 .... 2
T5 0 0 0 0 .... 1
In the algorithm actually a weighted summation of AS and informativeness is used.
0.3 x informativeness + 0.7 x AS

16. MO
● Objectives : each individual in
the other subpopulation.
● MO: number of individuals that
dominate it. f2
non-dominated
● Non-dominated individuals dominated
have the highest fitness value.
f1

17. Performance Measures
● Objective Fitness (OF)
– Evaluation against a fix set of test cases
– Here we use "all possible test cases" since we have
picked problems with small sizes.
● Objective Fitness Correlation (OFC)
– Correlation between OFs and fitness values in the
coevolution (subjective fitness, SF).

18. Experimental Setup
● Controlled experiments: GAAS
– GA with AS from exhaustive evaluation.
● Compare the OF based on the same number of
interactions.

19. Test Problems
● Majority Function Problem (MFP)
– 1D cellular automata problem
– Two parameters: radius (r) and problem size (n)
A sample IC with n = 9 0 1 0 1 0 0 1 1 1
neighbor bits
target bit
Input 000 001 010 011 100 101 110 111
A sample rule with r = 1
Output 0 0 0 1 0 1 1 1
boolean-vector representation of this rule

20. Test Problems
● Majority Function Problem (MFP)

21. Test Problems
● Symbolic Regression Problem (SRP)
– Curve fitting with Genetic Programming trees
– Two measures: sum of error and hit
+ f(x)
original function
GP Tree
regression curve
hit
* +
- x x x
x x
2x
x

22. Test Problems
● Parity Problem (PP)
– Determine odd/even for the number of 1's in a bit
string
– Two parameter: odd/even and bit string length (n)
A problem with n = 10
0 1 0 1 0 0 1 1 11
A solution tree

23. Test Problems: PP
5-even Parity
Boolean-vector 0 0 0 1 0 false (0)
D0 D1 D2 D3 D4
0
AND false
GP Tree
1 0
OR AND
1 1 0
NOT AND D2 NOT OR AND
0
D0 D3 D0 D1 D1 D2
0 1 0 0 0 0

24. Results of MFP (r=2, n=9)

25. Results of MFP (r=2, n=9)

26. Results of SRP 6 4
x −2x x
2

27. Results of SRP 6 4
x −2x x
2

28. Results of PP (odd, n=10)

29. Results of PP (odd, n=10)

30. Summary of Results

31. Multi-objective Approach
● One run for COMO in
MFP.
● OF drops when NDR
rises.
● Why high NDR?
– Duplicate solutions
– Too many objectives

32. MO approach to improve WI
MFP
MO-WS-WI

33. MO approach to improve WI
SRP
MO-AS-WI
MO-WS-WI
WeiSum-AS-WI
MO-AS-AI
MO-WS-AI

34. MO approach to improve WI
PP
MO-AS-WI

35. Conclusions
● MO2 approach with weighted informativeness
(MO-AS-WI and MO-WS-WI) outperforms other
evaluation methods in coevolution.
● MO1 approach does not work well because
there are usually too many objectives. This can
be represented by a high NDR and results in a
random search.
● Coevolution is efficient for the MFP and SRP.

36. Issues
● Test problems used are small, and there is not
proof of generalizability to larger problems.
● Implication to statistical learning: select not only
difficult but also informative data for training.

37. Question?

38. Thank you!

39. Average Score
Solutions
S1 S2 S3 S4 S5
T1 0 1 0 0 1 2 0.4
T2 0 0 1 1 0 2 0.4
Test T3 0 1 1 0 0 2 0.4
cases T4 1 0 0 0 0 2 0.4
T5 1 0 1 0 0 2 0.4
2 2 3 1 1
0.4 0.4 0.6 0.2 0.2
Max(O(m),O(n))

40. Weighted Score
Solutions
S1 S2 S3 S4 S5
T1 0 1 0 0 1 2
T2 0 0 1 1 0 2
Test T3 0 1 1 0 0 2
cases T4 1 0 0 0 0 2
T5 1 0 1 0 0 2
2 2 3 1 1
Max(O(m),O(n))

41. Average Informativeness
Max(O(mn2),O(nm2))

42. Weighted Informativeness
Max(O(mn2),O(nm2))

43. MO
Max(O(mn2),O(nm2))