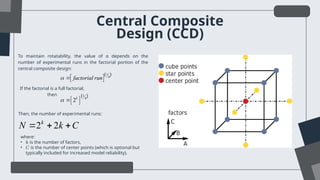
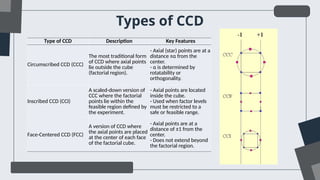
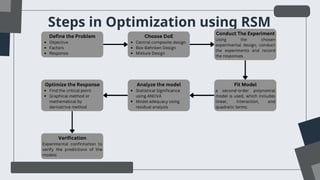
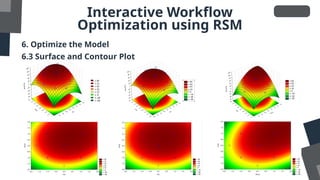
The document discusses the Design of Experiments (DOE) and Response Surface Methodology (RSM) for optimization in various fields such as engineering and science. It outlines the key components of DOE, types of experimental designs, and the steps involved in conducting experiments and analyzing results. Additionally, it demonstrates the application of RSM using TIBCO Statistica, focusing on optimizing the adsorption capacity of activated carbon for methylene blue removal.

1. TIBCO Statistica
OPTIMIZATION
USING RSM
Universitas Diponegoro | Faculty of Engineering | 2024
By: Dani Puji Utomo
Department of Chemical Engineering

2. DAFTAR ISI
Design of Experiment (DOE)
Optimization Method
Introduction of RSM
TIBCO Statistica
DOE using Statistica
RSM Optimization using Statistica
01
02
03
04
05
06

3. Design of Experiment (DoE) is a
systematic method used to plan,
conduct, analyze, and interpret
controlled tests to evaluate the
factors that influence a process or
product. The goal is to identify cause-
and-effect relationships while
maximizing information and
minimizing resource usage. DoE is
widely used in fields such as
engineering, science, and business
for process optimization, quality
improvement, and innovation.
Design of Experiment
Key Components of DoE
1.Factors: Independent variables that are hypothesized to
affect the outcome of the experiment. Examples include
temperature, pressure, or material type.
2.Levels: The specific values or settings of a factor, such as
"low" and "high," or numeric values like 50°C and 100°C.
3.Response Variable: The dependent variable that is measured
to evaluate the effect of the factors. For instance, the strength
of a material or the yield of a chemical reaction.
4.Treatment: A specific combination of factor levels used in the
experiment.
5.Replication: Repeated observations or measurements under
identical conditions to estimate variability and improve
accuracy.
6.Randomization: Random assignment of treatments to
experimental units to reduce bias and ensure that results are
generalizable.
7.Blocking: Grouping experimental units with similar
characteristics to control for variability that is not of interest.

4. Steps in Designing an Experiment
1.Define the Objective: Clearly state the problem, objective, and expected outcomes of the
experiment.
2.Select Factors and Levels: Identify the factors to be studied and the levels at which they will
be varied.
3.Choose an Experimental Design:
⚬ Full Factorial Design: Tests all possible combinations of factors and levels.
⚬ Fractional Factorial Design: Tests only a subset of combinations, useful for large numbers
of factors.
⚬ Randomized Complete Block Design: Controls for variability by dividing experiments into
blocks.
⚬ Response Surface Methodology (RSM): Explores relationships between factors and
responses, often used for optimization.
4.Randomize and Assign Treatments: Randomly assign treatments to ensure unbiased results.
5.Conduct the Experiment: Execute the plan, ensuring consistency and accuracy in
measurement.
6.Analyze the Results: Use statistical tools like ANOVA (Analysis of Variance), regression
analysis, or other models to interpret the effects of factors on the response.
7.Draw Conclusions and Verify: Validate findings with additional experiments or real-world

5. Full Factorial Design
Full Factorial Design is an experimental design method where all possible
combinations of the levels of factors are tested. This approach allows for a thorough
examination of the individual effects of each factor as well as the interactions between
factors. It is often considered the "gold standard" for experiments when the goal is to
gain complete understanding of the system being studied.
Commonly represented as k ,
where:
k = number of levels for each
factor.
n = number of factors.
n Example of a 2-Level Full Factorial Design
Consider an experiment with 2 factors:
• Factor A: Temperature (low, high)
• Factor B: Pressure (low, high)
Each factor has 2 levels. A full factorial design includes 2^2 =4
runs:
1.Low Temperature, Low Pressure
2.Low Temperature, High Pressure
3.High Temperature, Low Pressure
4.High Temperature, High Pressure

6. Fractional Factorial Design
Fractional Factorial Design is a variation of the Full Factorial Design that reduces the
number of experimental runs by only testing a selected subset of all possible
combinations of factor levels. It is particularly useful when a full factorial experiment is
impractical due to time, cost, or resource constraints, especially with a large number of
factors.
fractional factorial design may
involve a 2 subset:
• p : The fraction of runs
omitted.
• 2 : The number of runs
conducted.
k−
p
k−
p

7. Randomized Complete Block Design
Randomized Complete Block Design (RCBD) is an experimental design used to control
for variability among experimental units by grouping them into blocks based on certain
characteristics that might influence the response variable. Within each block, treatments
are randomly assigned to the experimental units, ensuring that the comparison
between treatments is not confounded by block effects.
Key Features of RCBD
• Blocking: Experimental units are divided into blocks based on known sources of variability (e.g.,
location, time, or other conditions). Each block should contain experimental units that are as
similar as possible.
• Randomization: reatments are randomly assigned within each block to eliminate bias.
• Completeness: Every block contains all treatments, ensuring that each treatment is tested under
similar conditions.
• Control for Variability: Variability between blocks is accounted for, improving the precision of the
treatment effect estimation.

8. Response Surface
Method
Response Surface Methodology (RSM) is a set of statistical and mathematical
techniques used to model and analyze problems where a response (dependent variable)
is influenced by several factors (independent variables). The goal is to optimize the
response by finding the best levels of the factors. RSM is particularly useful in situations
where there is a need to fine-tune a process or product.
Design Types in RSM
1. Central Composite Design (CCD):
• Most commonly used RSM design.
• Combines a factorial design, center points, and axial
points.
• Allows for the estimation of quadratic effects.
2. Box-Behnken Design (BBD):
• Does not include extreme (axial) points.
• Useful for experiments where the range of factor
levels is limited.
• Requires fewer runs compared to CCD.
3. Doehlert Design:
• Efficient for experiments with a high number of
factors.
• Ensures uniform precision over the experimental
space.
4. Face-Centered Central Composite Design
(FCCCD):
• A variation of CCD where axial points are located
on the faces of the factorial cube.
5. Mixture Design
• ‘In a mixture design, the sum of the component
proportions is always fixed

9. Central Composite
Design (CCD)
To maintain rotatability, the value of α depends on the
number of experimental runs in the factorial portion of the
central composite design:
If the factorial is a full factorial,
then
  
1
4
factorial run
 
 
1
4
2k
  
 
Then, the number of experimental runs:
2 2
k
N k C
  
where:
• 𝑘 is the number of factors,
• 𝐶 is the number of center points (which is optional but
typically included for increased model reliability).

10. Types of CCD
Type of CCD Description Key Features
Circumscribed CCD (CCC)
The most traditional form
of CCD where axial points
lie outside the cube
(factorial region).
- Axial (star) points are at a
distance ±α from the
center.
- α is determined by
rotatability or
orthogonality.
Inscribed CCD (CCI)
A scaled-down version of
CCC where the factorial
points lie within the
feasible region defined by
the experiment.
- Axial points are located
inside the cube.
- Used when factor levels
must be restricted to a
safe or feasible range.
Face-Centered CCD (FCC)
A version of CCD where
the axial points are placed
at the center of each face
of the factorial cube.
- Axial points are at a
distance of ±1 from the
center.
- Does not extend beyond
the factorial region.

11. Box-Behnken Design
(BBD)
Box-Behnken Design (BBD) is a type of experimental design used in Response
Surface Methodology (RSM) to explore the relationships between several explanatory
variables and a response variable. It is particularly useful for optimizing processes and
finding optimal settings for variables with fewer experimental runs compared to
traditional designs, such as full factorial designs.
 
2 1
N k k C
  
where:
• 𝑘 is the number of factors,
• 𝐶 is the number of center points (which is optional but
typically included for increased model reliability).
The experimental runs are designed using combinations of three levels for
each factor, but there are no combinations at the extremes of the factor
space. This results in a spherical or circular design structure.
In a Box-Behnken design for k factors, the experimental runs are
arranged as follows:
• The design includes factorial points and center points.
• There are no corner points (i.e., the extreme values for all factors
simultaneously).
• The runs are arranged so that each factor is varied at low, medium,
and high levels.

12. Optimization using RSM
Optimization in RSM refers to finding the input values (or factor settings) that
result in the best possible outcome (response), typically by maximizing or
minimizing a certain response variable.
Response Surface Methodology (RSM) is a collection of mathematical and
statistical techniques used to model and analyze the relationship between a
response variable and multiple input (predictor) variables. It is primarily used for
optimizing processes, improving product quality, and identifying optimal factor
settings in a system.
Typically, a second-order polynomial model is used, which includes linear,
interaction, and quadratic terms:
2 2 2
0 1 1 2 2 3 3 12 1 2 13 1 3 23 2 3 11 1 22 2 33 3
Y X X X X X X X X X X X X
         
          
Where:
• Y is the response variable
• X1, X2, X3​are the factors (independent variables),
• β0, β1, β2,… are the regression coefficients,
• ϵ is the error term.

13. Steps in Optimization using RSM

14. Tools in Optimization using RSM
TIBCO Statistica®
is a flexible analytics system, which allows users to, create analytic
workflows that are packaged and published to business users, explore interactively
and visualize, create and deploy statistical, predictive, data mining, machine learning,
forecasting, optimization, and text analytic models.
Latest Version : TIBCO Statistica™ 14.0.0
Design–Expert is a statistical software package from Stat-Ease Inc. that is specifically
dedicated to performing design of experiments (DOE). Design–Expert offers
comparative tests, screening, characterization, optimization, robust parameter
design, mixture designs and combined designs.
Latest Version: Design-Expert v23.1
JASP (Jeffreys’s Amazing Statistics Program) is a free and open-source program
for statistical analysis supported by the University of Amsterdam. It is designed to be
easy to use, and familiar to users of SPSS.
Latest Version: JASP 0.19.1.

15. User Interface TIBCO Statistica

16. Interactive Workflow
Optimization using RSM
1. Define The Problem
Optimization of adsorption capacity of Elaeis
guineensis-activated carbon for methylene blue
removal
Factors with coded value
Factors Low Level Mid Level High Level
Particle size (Mesh) 32 48 64
Temperature (C) 500 600 700
Time (h) 1 2 3
Response:
 
0
0
% 100%
t
C C
removal
C

 
In this equation,
• C0 are the solution concentrations at initial (mg/L)
• Ct are the solution concentration at time t (mg/L)
Factors Low Level Mid Level High Level
Particle size (Mesh) -1 0 1
Temperature (C) -1 0 1
Time (h) -1 0 1
 
0
i i
i
i
X X
x
X



Factors with original value
In this equation,
• xi is the coded value of ith
factors / independent
variables
• Xi is original value of ith
factors
• Xi
0
is original value of center point
• ΔXi is the difference between maximum and

17. Interactive Workflow
Optimization using RSM
2. Choose type of DoE
For this study, Central Composite Design is selected
• Define Number of Runs
k = number of factors = 3
2 2
k
N k C
  
3
3
2 2(3) 2 16
2 2(3) 3 17
N
N
   
   
• Define extreme points (star points)
 
1
4
2 1,6818
k
  
Standard
Run
2**(3) central composite, nc=8 ns=6 n0=2
Runs=16
PS/Mesh T/C t/h
1 -1,0000 -1,0000 -1,0000
2 -1,0000 -1,0000 1,0000
3 -1,0000 1,0000 -1,0000
4 -1,0000 1,0000 1,0000
5 1,0000 -1,0000 -1,0000
6 1,0000 -1,0000 1,0000
7 1,0000 1,0000 -1,0000
8 1,0000 1,0000 1,0000
9 -1,6818 0,0000 0,0000
10 1,6818 0,0000 0,0000
11 0,0000 -1,6818 0,0000
12 0,0000 1,6818 0,0000
13 0,0000 0,0000 -1,6818
14 0,0000 0,0000 1,6818
15 (C) 0,0000 0,0000 0,0000
16 (C) 0,0000 0,0000 0,0000

18. Interactive Workflow
Optimization using RSM
3. Conduct the experiment
Standard
Run
2**(3) central composite, nc=8 ns=6
n0=2 Runs=16 Response
(%)
PS/Mesh T/C t/h
1 -1,0000 -1,0000 -1,0000 8,0
2 -1,0000 -1,0000 1,0000 21,8
3 -1,0000 1,0000 -1,0000 15,5
4 -1,0000 1,0000 1,0000 67,8
5 1,0000 -1,0000 -1,0000 12,8
6 1,0000 -1,0000 1,0000 30,2
7 1,0000 1,0000 -1,0000 34,5
8 1,0000 1,0000 1,0000 92,0
9 -1,6818 0,0000 0,0000 38,3
10 1,6818 0,0000 0,0000 60,9
11 0,0000 -1,6818 0,0000 18,9
12 0,0000 1,6818 0,0000 75,1
13 0,0000 0,0000 -1,6818 20,2
14 0,0000 0,0000 1,6818 73,2
15 (C) 0,0000 0,0000 0,0000 72,8
16 (C) 0,0000 0,0000 0,0000 73,1
Experimental Results

19. Interactive Workflow
Optimization using RSM
4. Fitting Model
2 2 2
1 2 3 1 2 3
1 2 1 3 2 3
74,00 6,91 16,95 16,85 10,80 11,72 11,82
3,75 1,10 9,82
Y X X X X X X
X X X X X X
      
  
2 1
0
1 1 1
n n n n
i i i i ij i j
i i i j
Y x x x x
   

  
 
    
 
 
   

20. Interactive Workflow
Optimization using RSM
5. Model Analysis
5.1. Significance Analysis using ANOVA
a. Formulate the hypotheses
• Null Hypothesis = The model has no significant effect on the response
• Alternative Hypothesis: The model has significant effect on the response
b. Sum of Squares
• Total Sum of Squares (SST): Measures the total variability in the response variable.
• Regression Sum of Squares (SSR): Measures the variability explained by the model.
• Residual Sum of Squares (SSE): Measures the variability due to random error or unexplained
variation
c. Mean of Squares
• Mean Square for Regression (MSR): MSR=SSR/p with p is the number of model parameters
• Mean Square for Error (MSE): MSE= SSE/(n-p-1)​, where n is the total number of data points.
d. F-test
• The F-statistic is calculated by dividing the mean square for regression (MSR) by the mean
square for error (MSE)
d. p-value
• A low p-value (typically p<0.05) indicates that the model is statistically significant)

21. Interactive Workflow
Optimization using RSM
5. Model Analysis
5.1. Significance Analysis using ANOVA
• Red color indicates significant Effects
• Black color indicates non significant Effects

22. Interactive Workflow
Optimization using RSM
5. Model Analysis
5.1. Significance Analysis using ANOVA

23. Interactive Workflow
Optimization using RSM
5. Model Analysis
5.2. Model Adequacy Check
• R2
= 0,9666
• Adj-R2
= 0,9165

24. Interactive Workflow
Optimization using RSM
6. Optimize the Model
6.1 Single Response Optimization 6.2 Multiple Responses Optimization
(later)
• Put value 0 desirability for
undesired level value
• Put value 1 desirability for
desired level value
Suitable for optimizing
multiple responses with trade-
off profile,
for example in maximizing the
Yield and minimizing
Production Cost
Optimized Value
• PS =
0,6255
• Temp = 1,3738
• Time = 1,3125

25. Interactive Workflow
Optimization using RSM
6. Optimize the Model
6.3 Surface and Contour Plot

26. Interactive Workflow
Optimization using RSM
6. Verification
Conduct experimental verification
Optimized Value  Convert to original
value
• PS = 0,6255
• Temp = 1,3738
• Time = 1,3125
0
i i i i
X X x X
 
 
16 0,6255 48 58,01
PS    
 
100 1,3738 600 738
Temp    
 
1 1,3125 2 3,31
Time    
Verif Run Predicted Experiment SSR
Run 1 98,86 98,27 0,3481
Run 2 98,86 97,89 0,9409
Run 3 98,86 99,12 0,0676
Total 1,3566
Error 0,8236
% error 0,83%

27. Interactive Workflow
Optimization using RSM
6.2 Simultaneous Optimization for Multiple Responses
• From the Prediction & Profiling Tab  Click on Response
Desirability Profiling
• Checklist the show desirability function
• Put value of 0.00; 0.50; and 1.00 for undesired, mid desired, and
very desired value level, respectively
• Set factors at Optimum Value
• You may set the factor grid by approximately 20 steps
• Click View to show the compound desirability optimization
• Click 3D response and contour icons to show the plot

28. Interactive Workflow
Optimization using RSM
The Optimum Value for Desired Response

29. Interactive Workflow
Optimization using RSM
3D Surface and Contour Compound Plot