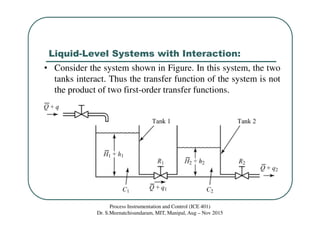
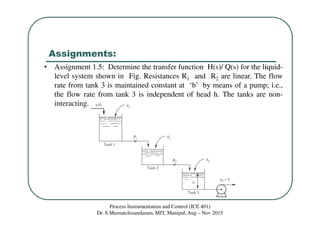
The document discusses mathematical modeling of interacting and non-interacting liquid-level systems in a process instrumentation and control class, outlining equations and transfer functions for each system type. It highlights the differences in transient responses for systems based on interaction between tanks, presenting specific assignments for calculating transfer functions. Relevant references for further reading on modern control engineering and measurement basics are also provided.

1. ICE401: PROCESS INSTRUMENTATION
AND CONTROL
Class 8: Mathematical Modeling of
Interacting and Non-Interacting Level
Systems
Dr. S. Meenatchisundaram
Email: meenasundar@gmail.com
Process Instrumentation and Control (ICE 401)
Dr. S.Meenatchisundaram, MIT, Manipal, Aug – Nov 2015

2. Liquid-Level Systems with Interaction:
Process Instrumentation and Control (ICE 401)
Dr. S.Meenatchisundaram, MIT, Manipal, Aug – Nov 2015
• Consider the system shown in Figure. In this system, the two
tanks interact. Thus the transfer function of the system is not
the product of two first-order transfer functions.

3. Liquid-Level Systems with Interaction:
Process Instrumentation and Control (ICE 401)
Dr. S.Meenatchisundaram, MIT, Manipal, Aug – Nov 2015
• In the following, we shall assume only small variations of the
variables from the steady-state values. We can obtain the
following equations for this system:
(6.1)
(6.2)
(6.3)
(6.4)
1 2
1
1
h h
q
R
−
=
1
1 1
dh
q q C
dt
− =
2
2
2
h
q
R
=
2
1 2 2
dh
q q C
dt
− =

4. Liquid-Level Systems with Interaction:
Process Instrumentation and Control (ICE 401)
Dr. S.Meenatchisundaram, MIT, Manipal, Aug – Nov 2015
• Substituting eqn. 6.1 into eqn. 6.2 and eqn. 6.4, solving and
taking Laplace transformation yields:
(6.5)
• Assignment 1.4: Calculate the transfer function of the above
system for
( )
2
2
1 1 2 2 1 1 2 2 2 1
( ) 1
( ) 1
Q s
Q s RC R C s RC R C R C s
=
+ + + +
2( )
?
( )
H s
Q s
=

5. Liquid-Level Systems without Interaction:
Process Instrumentation and Control (ICE 401)
Dr. S.Meenatchisundaram, MIT, Manipal, Aug – Nov 2015
• In the figure, the outlet flow from tank 1 discharges directly
into the atmosphere before spilling into tank 2, and the flow
through R1 depends only on h1 .
• The variation in h2 in tank 2 does not affect the transient
response occurring in tank 1. This type of system is referred
to as a non-interacting system.

6. Liquid-Level Systems without Interaction:
Process Instrumentation and Control (ICE 401)
Dr. S.Meenatchisundaram, MIT, Manipal, Aug – Nov 2015
• In the following, we shall assume only small variations of the
variables from the steady-state values. We can obtain the
following equations for this system:
(6.6)
• For tank 2,
(6.7)
(6.8)
Substitute 6.8 into eqn. 6.7, yields
1
1 1
dh
q q A
dt
− =
1 2
1 2
1 2
and
h h
q q
R R
= =
2
1 2 2
dh
q q A
dt
− =

7. Liquid-Level Systems without Interaction:
Process Instrumentation and Control (ICE 401)
Dr. S.Meenatchisundaram, MIT, Manipal, Aug – Nov 2015
(6.9)
(6.10)
1
1
( ) 1
( ) 1
Q s
Q s sτ
=
+
2 2
1 2
( ) 1
( ) 1 1
H s R
Q s s sτ τ
=
+ +

8. Assignments:
Process Instrumentation and Control (ICE 401)
Dr. S.Meenatchisundaram, MIT, Manipal, Aug – Nov 2015
• Assignment 1.5: Determine the transfer function H(s)/ Q(s) for the liquid-
level system shown in Fig. Resistances R1 and R2 are linear. The flow
rate from tank 3 is maintained constant at ‘b’ by means of a pump; i.e.,
the flow rate from tank 3 is independent of head h. The tanks are non-
interacting.

9. References:
• Modern Control Engineering, 5th Edition, by Katsuhiko Ogata
• Measurement and Control Basics, 3rd Edition, by Thomas A.
Hughes.
• Process Control: Concepts Dynamics And Applications by Shio
Kumar Singh
Process Instrumentation and Control (ICE 401)
Dr. S.Meenatchisundaram, MIT, Manipal, Aug – Nov 2015