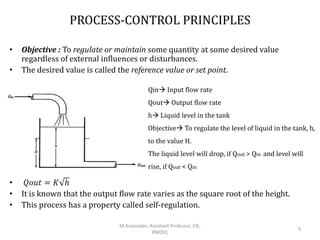
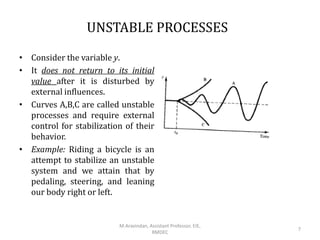
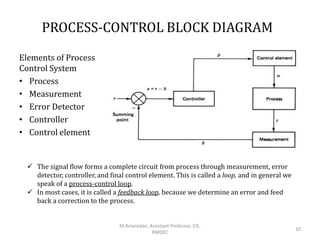
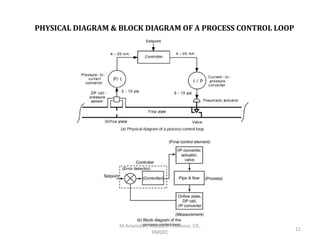
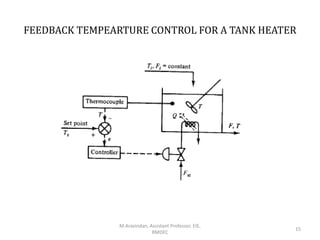
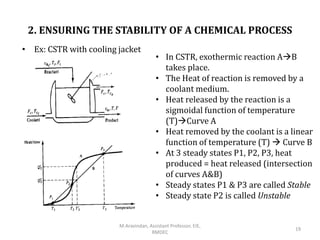
This document introduces automatic process control systems. It discusses the basic concepts of process control including the need for control systems to regulate variables and maintain stability despite disturbances. The key elements of a process control loop are identified as the process, measurement, error detection, controller and control element. Process variables are classified and a liquid level control system is used to illustrate modeling concepts. The document provides an overview of process control fundamentals.