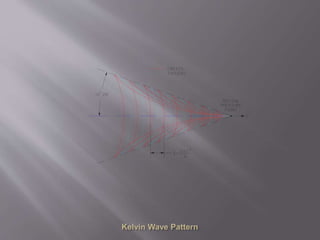
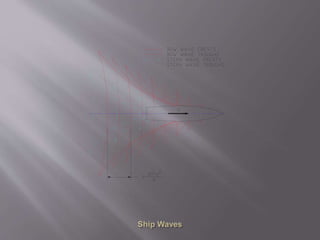
This document discusses wave resistance in ships. It explains that wave resistance increases significantly at high speeds as waves generated by the ship grow larger. It also describes how the interference of bow and stern waves can result in either favorable or unfavorable wave patterns depending on their phase relationship. Finally, it discusses how ship speed is ideally operated in a "hollow" of the wave resistance curve where interference is favorable and resistance is lower.

2.  There are two main components of resistance
 Viscous resistance
 Wave resistance
 Wave resistance is associated with the waves
generated by a ship alone.
 At low speeds (Froude numbers), wave
resistance is a small part of total resistance.

3.  At very high speeds (Fn more than about 0.45),
wave resistance increases so much that
conventional displacement type vessels cannot
go at such high speeds.
 It is necessary to use unconventional hull
forms for ships of very high speed.

4.  A three-dimensional body moving in water has
a pressure distribution around it.
 In case of a ship, the free surface will rise at
regions of high pressure and fall at regions of
low pressure.
 A moving pressure distribution will give rise to
free surface waves accompanying the body.
 This was observed by W. Froude, who made a
sketch showing the waves generated by a ship.

6.  The waves generated by a "moving pressure point”
were studied by Lord Kelvin. (Figure).
 The main features of the Kelvin wave pattern are :
 The pressure point generates a series of transverse waves and a
series of diverging waves.
 The transverse waves are slightly curved convex forward,
travel at the same speed V as the pressure point, have a wave
length appropriate to the wave speed (i.e. )
 The diverging waves emanate from the pressure point and join
the transverse waves that lie on lines radiating from the
pressure point on either side of the direction of motion at
angles of 19o
28’ (sin-1
1/3).
2
2 V g 

8.  The waves generated by a ship in calm water have the
similar features.
 The moving pressure distribution of the ship can be
regarded as an assembly of pressure points all
producing Kelvin wave patterns that are superposed
on each other.
 There is a bow wave system and a stern wave system,
each with diverging and transverse waves (Figure) :
 Each system lies within lines making an angle with direction of
motion; the angle depends on the hull form.
 The bow transverse waves start with a crest aft of the bow.
 The stern transverse waves start with a trough forward of the
stern.
 The stern wave system is superimposed on the bow wave
system.
 Diverging waves are steeper and therefore more visible.
 The combined wave system spreads far and wide behind the
ship with the wave heights reducing and finally dying out.

11.  The superposition of the stern waves on the
bow waves results in wave interference that may
be favourable or unfavourable.
 If the transverse waves from the bow are in
phase with the transverse waves from the stern,
i.e. the crests of the bow waves coincide with
the crests of the stern waves, the resulting
waves will have the maximum height, and the
wave resistance will be larger than the value it
would have if there was a phase difference.
Considering resistance, this is unfavourable
interference.

12.  If the bow waves and the stern waves are
completely out of phase, i.e. the crests of the
bow waves coincide with the troughs of the
stern waves, the resulting waves have smaller
heights and the wave resistance is lower :
favourable interference.
 Wave resistance does not increase steadily with
speed but has undulations. This is shown
clearly by a curve of wave resistance coefficient
as a function of Froude number, or a curve of
total resistance coefficient as a function of speed-
length ratio , V in knots, L in feet.
/V L

14.  The “humps and hollows” in a wave resistance
curve can also be explained by noting that a
deep wave trough at the stern will cause a
sharp increase in pressure resistance, while a
shallow trough or a crest will reduce the
pressure resistance, which is mostly wave
resistance. (Figure).
 The speeds or Froude numbers at which
favourable and unfavourable wave interference
(humps and hollows) occur can be calculated.

16.  mL = distance between first crest of bow transverse
waves and first crest of stern transverse waves.
n = number of complete wave lengths in the distance mL
Values of Froude number, Fn
Hump Hollow Hump Hollow
n Speed Speed n Speed Speed
1 0.520 0.736 6 0.212 0.222
2 0.368 0.425 7 0.197 0.204
3 0.300 0.329 8 0.184 0.190
4 0.260 0.278 9 0.173 0.178
5 0.233 0.245 10 0.164 0.169
 (Figure)

17.  The hump corresponding to n = 1 is called the “main
hump”, and the hump corresponding to n = 2 is called the
“prismatic hump” because it depends upon the prismatic
coefficient of the ship.
The design speed should preferably lie in a hollow.
At low Froude numbers, the wave length is small, there
are many waves between the bow and the stern and the
wave heights are small. The wave resistance is small and
interference effects are negligible.
As Froude number increases, the number of waves within
the ship length decreases, the wave heights increase and
the wave resistance becomes large and the interference
effects prominent.
As the Froude number approaches about 0.4, the wave
length approaches the length of the ship.

18.  Above a Froude number of 0.4, the wave length becomes
greater than the length of the ship, the first trough of the
bow waves starts nearing the stern, there is a large
decrease in pressure, particularly towards aft, resulting in
sinkage and aft trim, and a large increase in wave
resistance.
These effects reach their peak at Froude numbers around
0.5 (main hump). The sharp increase in wave resistance at
Froude numbers above 0.4 acts as a speed barrier for ships
of normal form and unconventional hull forms must be
used.

19.  Wave breaking resistance is closely related to wave
making resistance.
In ships with very full forebodies, the flow ahead of the
bow becomes unstable and the bow waves break resulting
in wave breaking resistance.
Wave breaking may be due to flow separation at the free
surface ahead of the bow.
Another view is that wave breaking occurs when the
streamlines at the bow have excessive curvature causing
flow instability.
Guidelines for avoiding wave breaking include making
the radius of curvature of the streamlines sufficiently large
(R>V2
/50, metric units), and limiting the half angle of
entrance and the slope of the tangent to the sectional area
curve at the forward end within limits.
Wave breaking resistance is not important for most ships.

21.  Appendages :
 Single screw ships : rudder, bilge keels and stabiliser
fins, skeg
 Twin screw ships : shaft brackets or bossings, open
shafts, multiple rudders
 “Negative appendages” : projections into the hull,
e.g. tunnels of lateral thrust units

22.  Appendage resistance from model tests :
 Appendage resistance = total resistance with
appendages – bare hull total resistance
 Difficulties:
 Accuracy of small appendages such as bilge keels
 Scaling problems : Reynolds number effects, laminar
flow
 Appendage scale factor

23.  Propulsion devices and their components not
considered as appendages
 Rudders in propeller slipstream
 Empirical formulas for resistance of individual
appendages
 Preliminary estimates of appendage resistance
as a percentage of total bare hull resistance

24. APPENDAGE RESISTANCE AS
PERCENTAGE OF BARE HULL RESISTANCE
Type of ship Values of Froude number
0.21 0.30 0.48
Large, fast, four screws 10-16 10-16 -
Small, fast, twin screws 20-30 17-25 10-15
Small, medium speed, twin screws 12-30 10-23 -
Large, medium speed, twin screws 8-14 8-14 -
All single screw ships 2 - 5 2 - 5 -

25.  Air and wind resistance RAA : D.W. Taylor’s
formula :
 CD is the drag coefficient
 is the density of air
 AT is the transverse projected area of the ship above
water
 VR is the relative head wind speed
 Typically CD = 1.2, = 1.225 kg per m3
1 2
2AA D air T RR C A V 
air
air

26.  Hughes method (slightly modified) to
determine RAA :
 Wind force
 VR = relative wind velocity
 = relative wind direction
 AL = longitudinal above water projected area
 AT = transverse above water projected area
 = angle of wind force to ship centre line
1 2 2
2
1 2 2
2
cos cos
sin sin
D air T R
D air L R
F C A V
F C A V
  
  





28.  Effect of wind velocity gradient – depends
upon relative magnitudes of ship speed and
absolute wind speed
 Yawing moment if centre of pressure of wind
force and centre of lateral resistance have a
large longitudinal separation : resulting drift
angle and use of rudder increase
hydrodynamic resistance
 Air and wind resistance may be reduced by
streamlining superstructure and deck houses –
but this works only in a head wind.