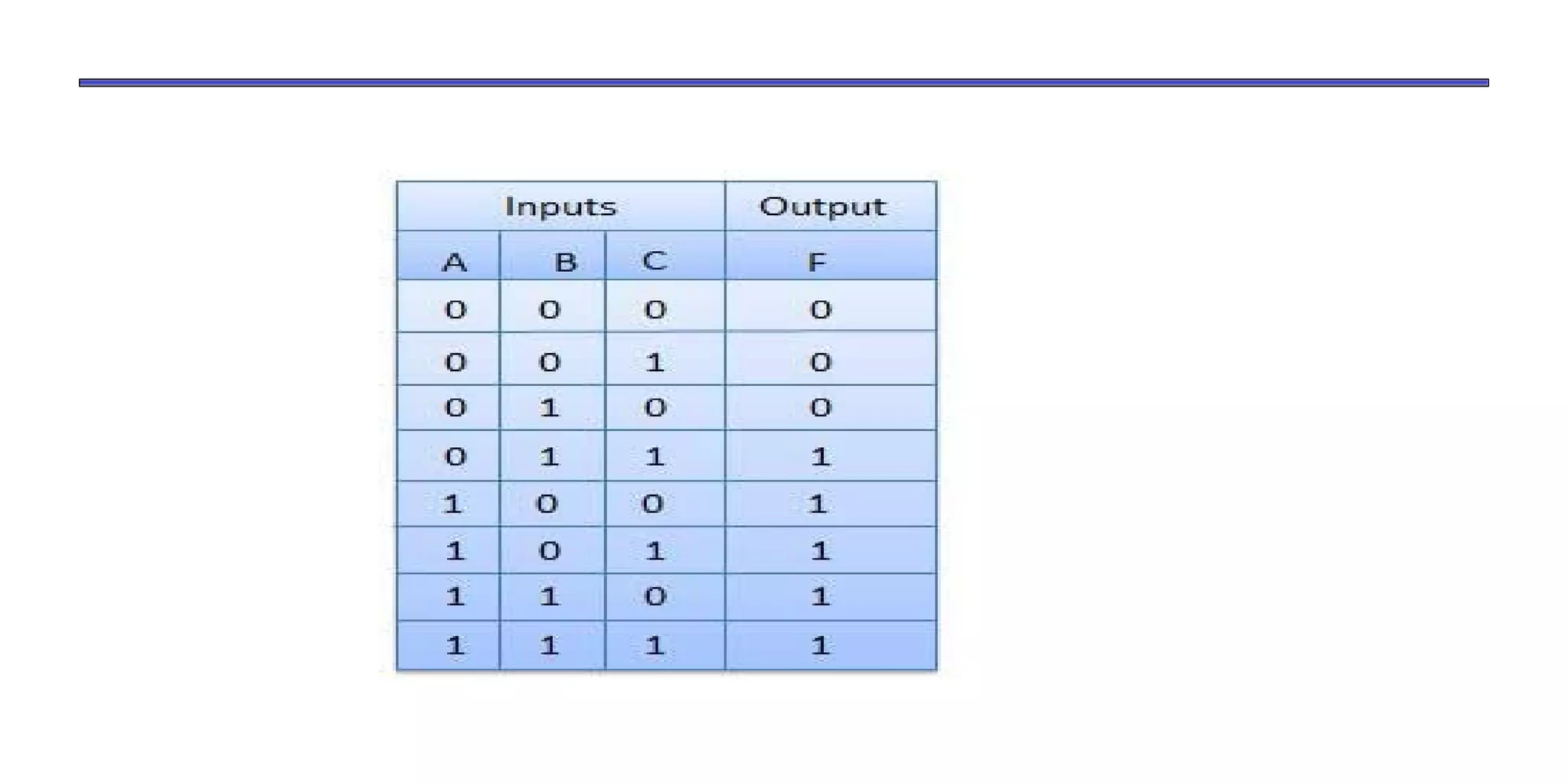
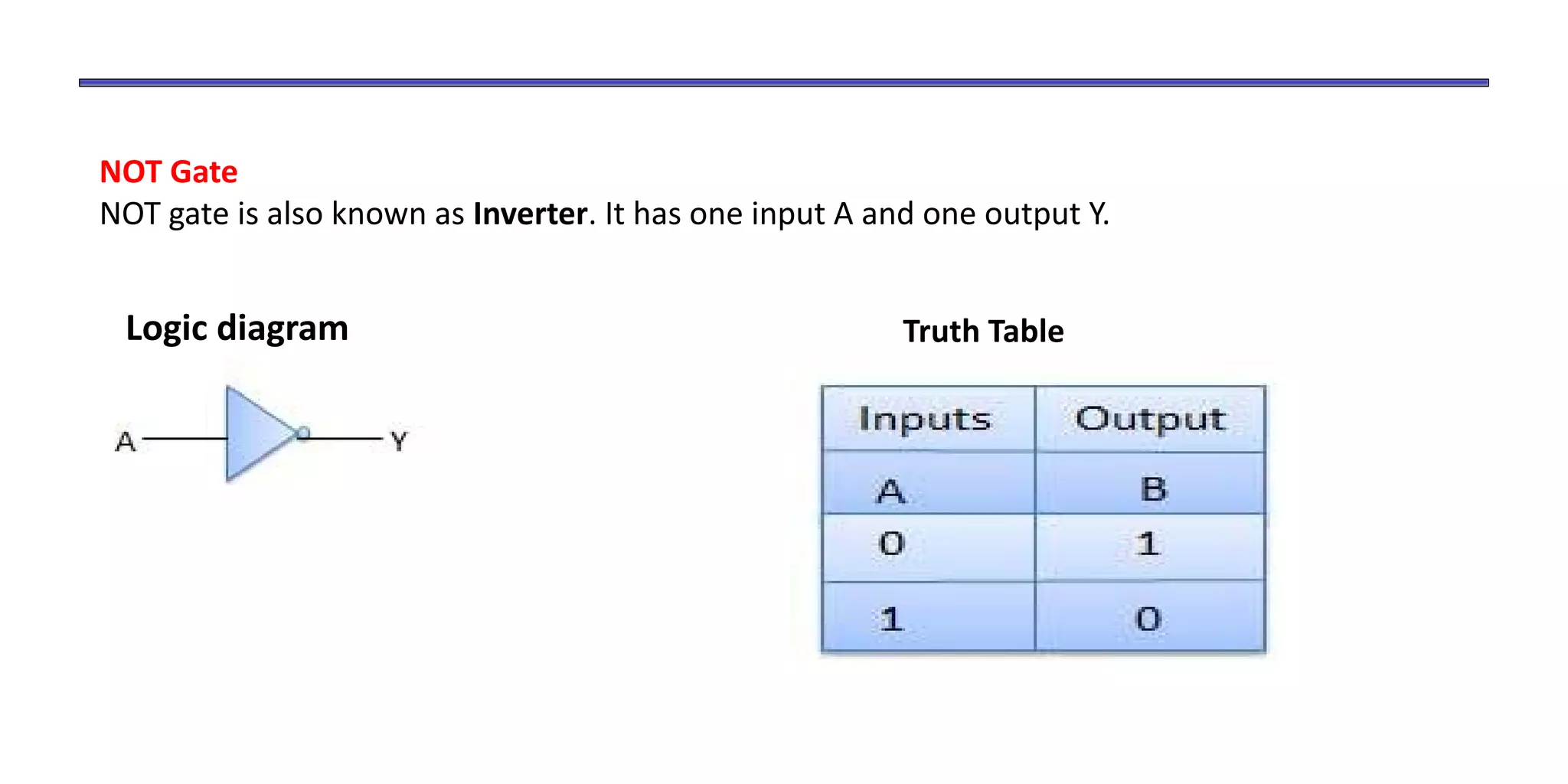
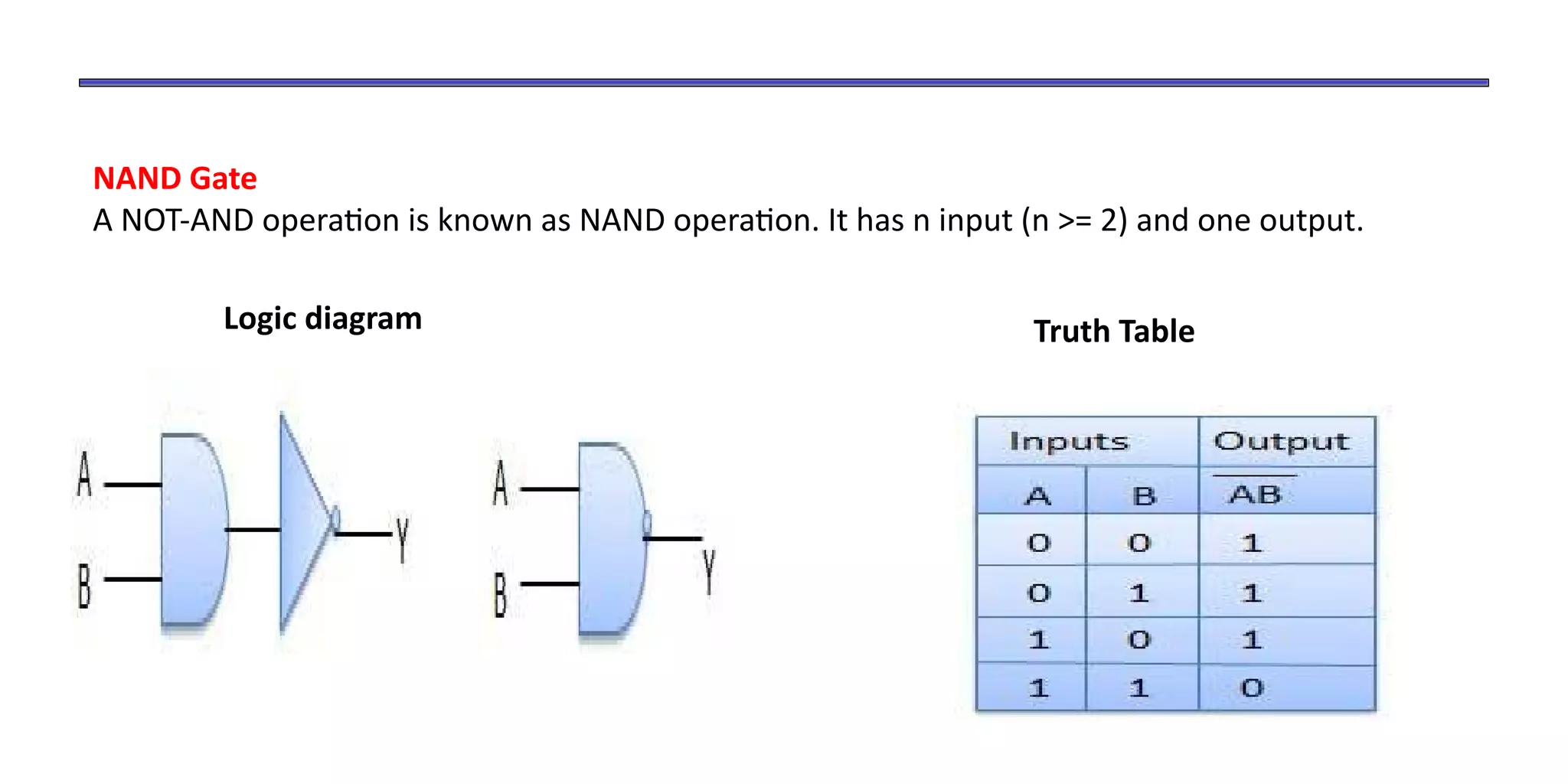
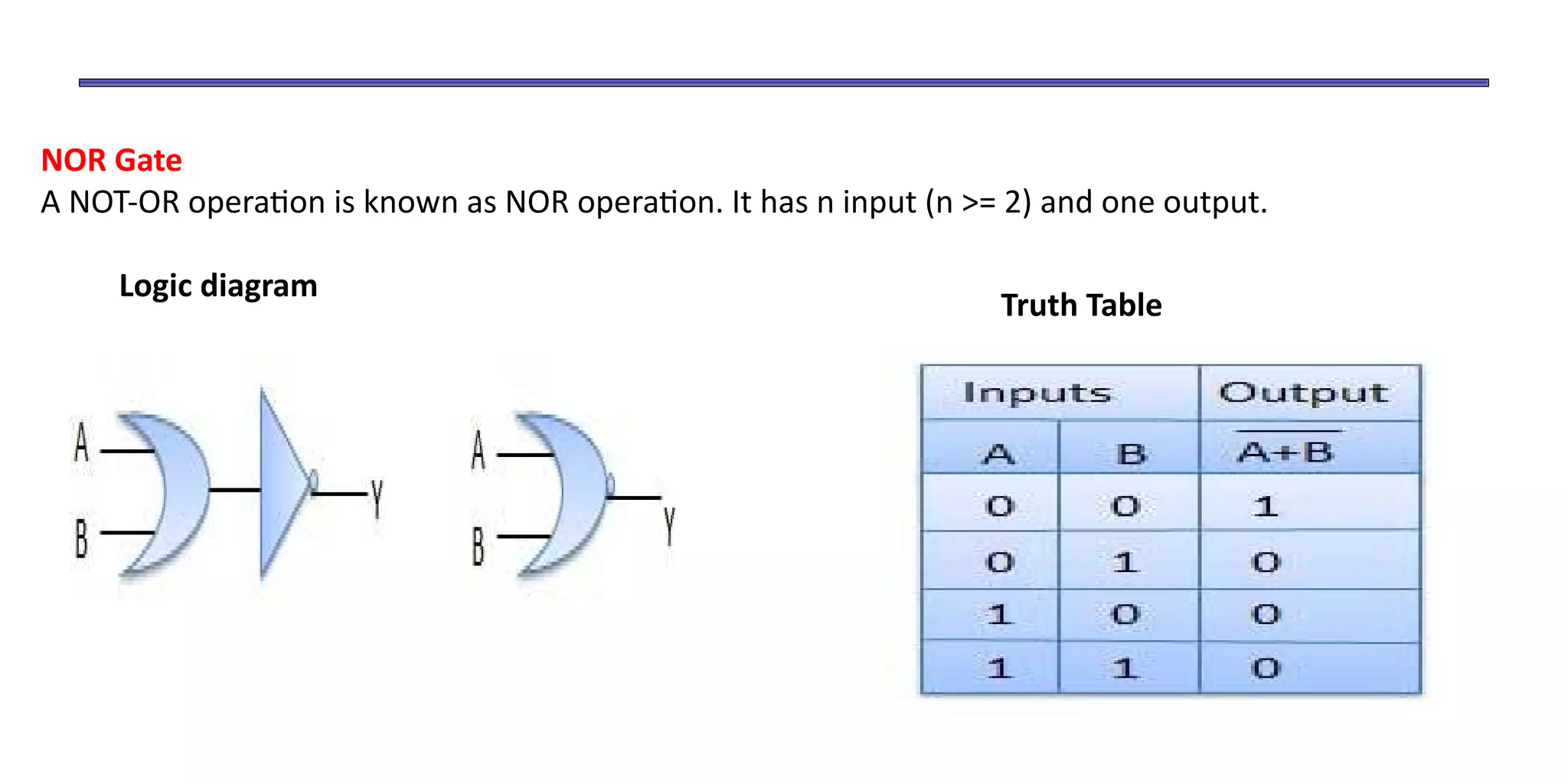
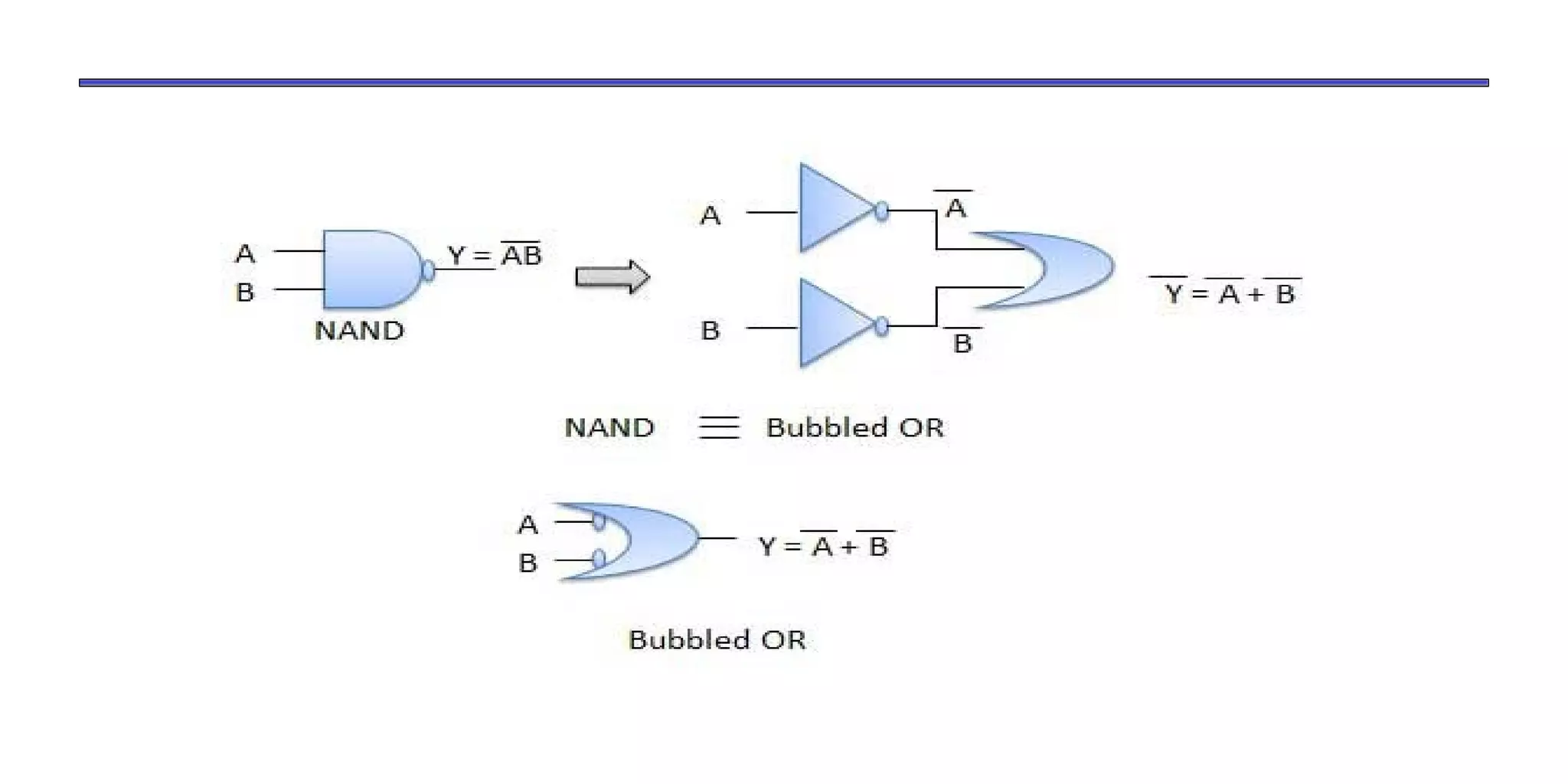
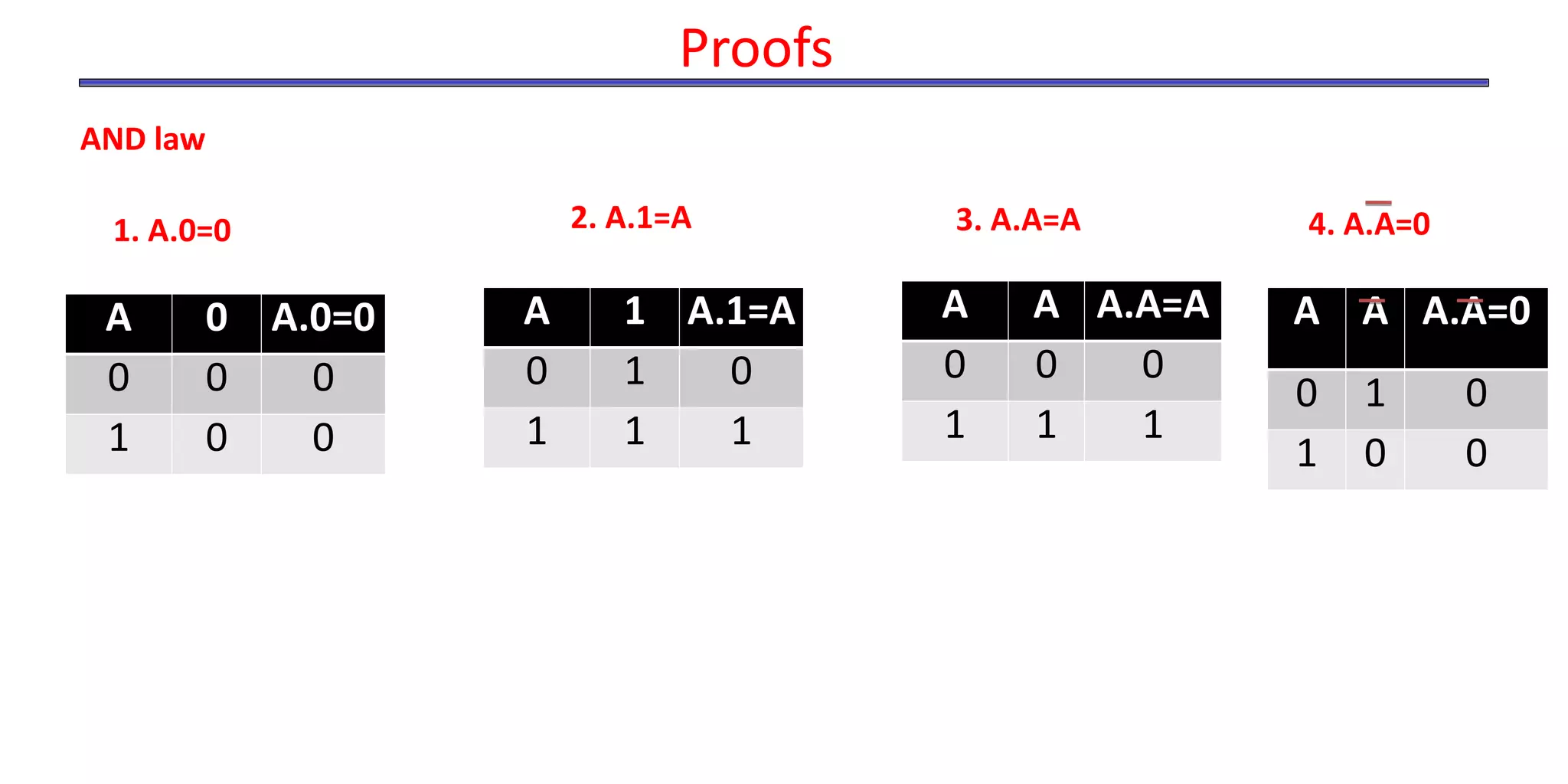
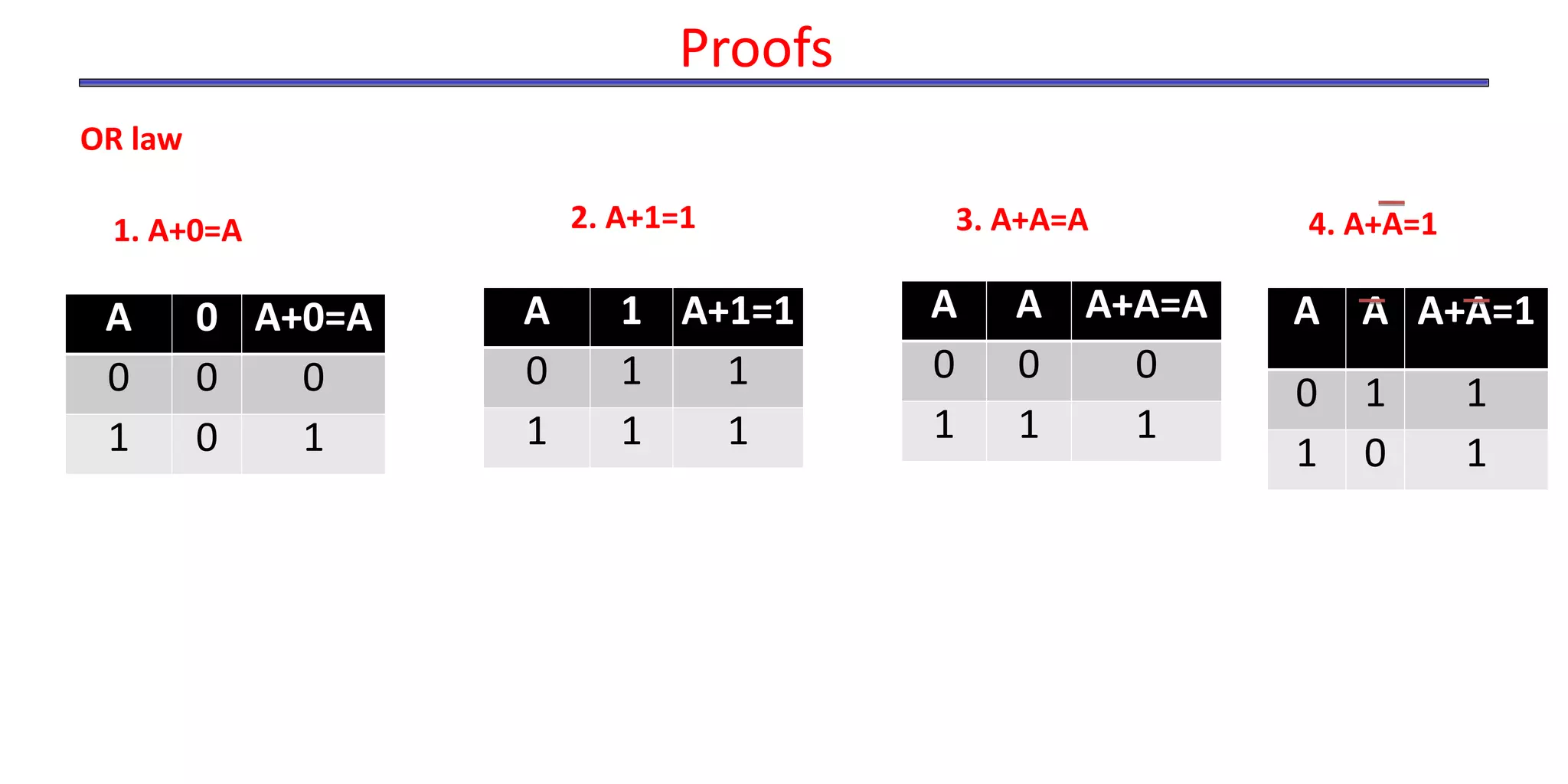
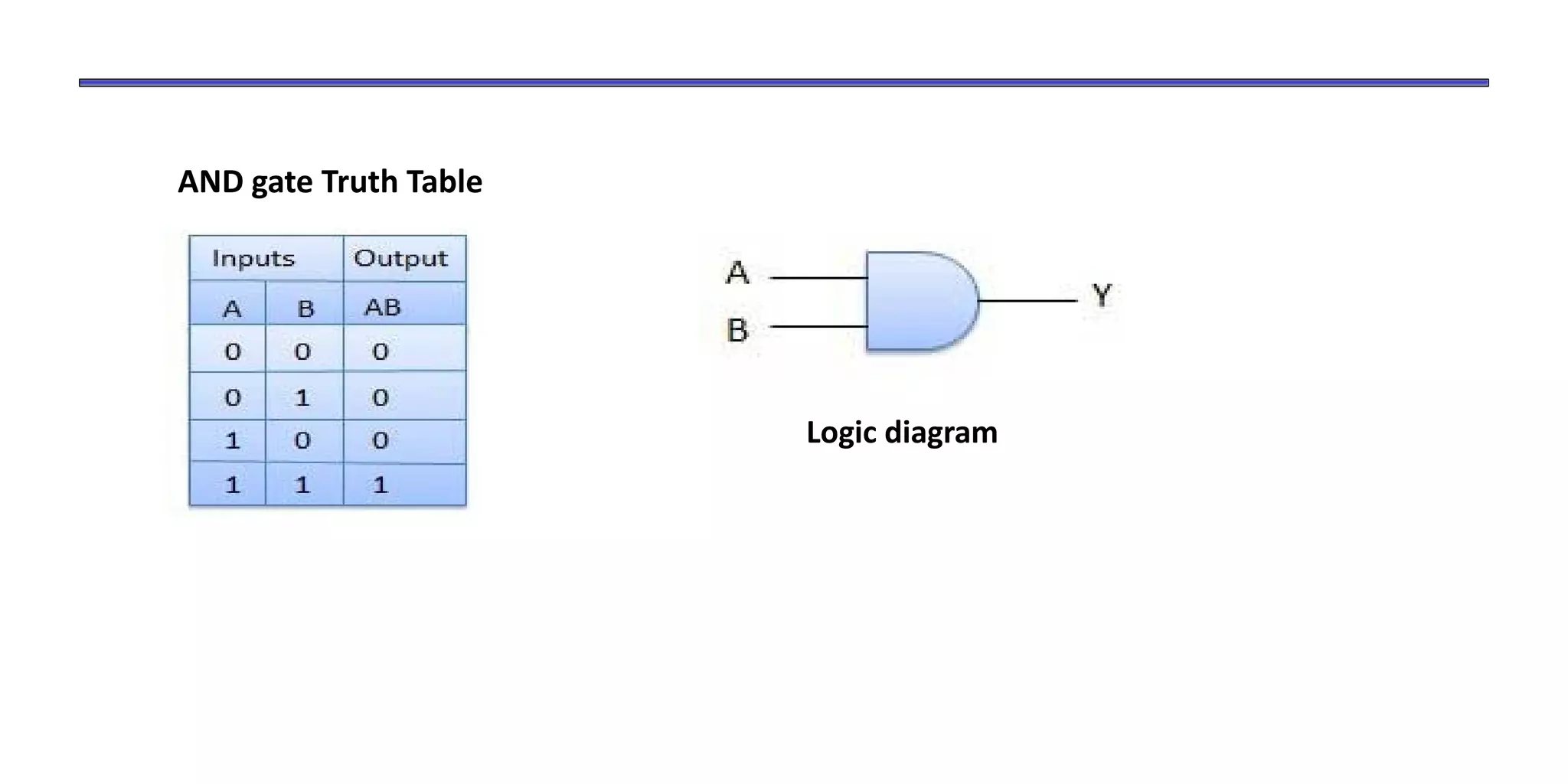
- Boolean algebra uses binary numbers (0 and 1) and logical operations (AND, OR, NOT) to analyze and simplify digital circuits. - It was invented by George Boole in 1854 and represents variables that can be either 1 or 0. - The document discusses Boolean operations, laws, logic gates, minimization techniques, and representing functions as sums of products.

1. Boolean algebra
By
P. THRIVENI, M.Tech
Assistant professor

2. Boolean Algebra

3. 2
Boolean Algebra Summary
• Boolean Algebra is used to analyze and simplify the digital (logic) circuits. It
uses only the binary numbers i.e. 0 and 1. It is also called as Binary
Algebra or logical Algebra.
• Boolean algebra was invented by George Boole in 1854. A variable whose
value can be either 1 or 0 is called a Boolean variable.
• AND, OR, and NOT are the basic Boolean operations.
• We can express Boolean functions with either an expression or a truth table.
• Now, we’ll look at how Boolean algebra can help simplify expressions,
which in turn will lead to simpler circuits.

4. Rules in Boolean Algebra
Following are the important rules used in Boolean algebra.
1. Variable used can have only two values. Binary 1 for HIGH and Binary 0 for LOW.
2. Complement of a variable is represented by an over bar (-). Thus, complement
of variable B is represented as . Thus if B = 0 then = 1 and B = 1 then = 0.
3. OR ing of the variables is represented by a plus (+) sign between them. For
example OR ing of A, B, C is represented as A + B + C.
4. Logical AND ing of the two or more variable is represented by writing a dot
between them such as A.B.C. Sometime the dot may be omitted like ABC.

5. Boolean Algebra Summary
• Recall that the two binary values have different names:
– True/False
– On/Off
– Yes/No
– 1/0
• We use 1 and 0 to denote the two values.
• The three basic logical operations are:
– AND
– OR
– NOT
• AND is denoted by a dot (·).
• OR is denoted by a plus (+).
• NOT is denoted by an overbar ( ¯ ), a single quote mark (') after

6. Boolean Laws
There are six types of Boolean Laws.
Commutative law
• Any binary operation which satisfies the following expression is referred to as
commutative operation.
• Commutative law states that changing the sequence of the variables does not have any
effect on the output of a logic circuit.

7. Associative law
•This law states that the order in which the logic operations are performed is
irrelevant as their effect is the same.
Distributive law
•Distributive law states the following condition.
Boolean Laws

8. AND law
•These laws use the AND operation. Therefore they are called as AND laws.
OR law
•These laws use the OR operation. Therefore they are called as OR laws.
Boolean Laws

9. INVERSION law
•This law uses the NOT operation. The inversion law states that double inversion of a
variable results in the original variable itself.
Boolean Laws

10. Proofs
A 0 A.0=0
0 0 0
1 0 0
AND law
1. A.0=0
A 1 A.1=A
0 1 0
1 1 1
2. A.1=A
A A A.A=A
0 0 0
1 1 1
3. A.A=A
A A A.A=0
0 1 0
1 0 0
4. A.A=0

11. Proofs
A 0 A+0=A
0 0 0
1 0 1
OR law
1. A+0=A
A 1 A+1=1
0 1 1
1 1 1
2. A+1=1
A A A+A=A
0 0 0
1 1 1
3. A+A=A
A A A+A=1
0 1 1
1 0 1
4. A+A=1

12. Proofs
Inversion law
1. A=A
A A A=A
0 1 0
1 0 1

13. •Logic gates are the basic building blocks of any digital system.
• It is an electronic circuit having one or more than one input and only one
output.
•The relationship between the input and the output is based on a certain logic.
Based on this, logic gates are named as AND gate, OR gate, NOT gate etc.
Logic gates
AND Gate
A circuit which performs an AND operation is shown in figure. It has n input
(n >= 2) and one output.

14. AND gate Truth Table
Logic diagram

15. OR Gate
A circuit which performs an OR operation is shown in figure. It has n input (n >= 2)
and one output.
Logic diagram
Truth Table

16. NOT Gate
NOT gate is also known as Inverter. It has one input A and one output Y.
Logic diagram Truth Table

17. NAND Gate
A NOT-AND operation is known as NAND operation. It has n input (n >= 2) and one output.
Logic diagram Truth Table

18. NOR Gate
A NOT-OR operation is known as NOR operation. It has n input (n >= 2) and one output.
Logic diagram
Truth Table

19. XOR Gate
XOR or Ex-OR gate is a special type of gate. It can be used in the half adder, full adder and subtractor.
The exclusive-OR gate is abbreviated as EX-OR gate or sometime as X-OR gate. It has n input (n >= 2)
and one output.
Logic diagram
Truth Table

20. XNOR Gate
XNOR gate is a special type of gate. It can be used in the half adder, full adder and subtractor. The
exclusive-NOR gate is abbreviated as EX-NOR gate or sometime as X-NOR gate. It has n input (n >= 2)
and one output.
Logic diagram
Truth Table

21. De Morgan's Theorems
De Morgan has suggested two theorems which are extremely useful in Boolean Algebra. The two
theorems are discussed below.
Theorem 1
• The left hand side (LHS) of this theorem represents a NAND gate with inputs A and B, whereas
the right hand side (RHS) of the theorem represents an OR gate with inverted inputs.
• This OR gate is called as Bubbled OR.

23. Table showing verification of the De Morgan's first theorem −

24. Theorem 2
•The LHS of this theorem represents a NOR gate with inputs A and B, whereas the RHS
represents an AND gate with inverted inputs.
•This AND gate is called as Bubbled AND.

26. Table showing verification of the De Morgan's second theorem −

27. •This theorem states that the dual of the Boolean function
is obtained by interchanging the logical AND operator with
logical OR operator and zeros with ones.
•For every Boolean function, there will be a corresponding
Dual function.
Duality principle

28. Group1 Group2
x + 0 = x x.1 = x
x + 1 = 1 x.0 = 0
x + x = x x.x = x
x + x’ = 1 x.x’ = 0
x + y = y + x x.y = y.x
x + y+zy+z = x+yx+y + z x.y.zy.z = x.yx.y.z
x.y+zy+z = x.y + x.z x + y.zy.z = x+yx+y.x+z
In each row, there are two Boolean equations and they are dual to each other. We can
verify all these Boolean equations of Group1 and Group2 by using duality theorem.
Duality principle

29. Consensus Theorem
Theorem1. AB+ A’C + BC = AB + A’C
Theorem2. (A+B). (A’+C).(B+C) =(A+B).( A’+C)
•The BC term is called the consensus term and is redundant.
•The consensus term is formed from a PAIR OF TERMS in which a variable (A) and its complement
(A’) are present;
•the consensus term is formed by multiplying the two terms and leaving out the selected variable
and its complement

30. Consensus Theorem1 Proof:
AB+A’C+BC=AB+A’C+(A+A’)BC
=AB+A’C+ABC+A’BC
=AB(1+C)+A’C(1+B)
= AB+ A’C

31. Minimization of Boolean functions
By
P. THRIVENI, M.Tech
Assistant professor

32. Algebraic Manipulation (Minimization of Boolean function)
•Boolean algebra is a useful tool for simplifying digital circuits.
•Why do it? Simpler can mean cheaper, smaller, faster.
Example:
Simplify F = x’yz + x’yz’ + xz.
= x’y(z + z’) + xz (Z+Z’=1)
= x’y•1 + xz
= x’y + xz

35. Example: Prove
x’y’z’ + x’yz’ + xyz’ = x’z’ + yz’
Proof:
x’y’z’+ x’yz’+ xyz’
= x’y’z’ + x’yz’ + x’yz’ + xyz’
= x’z’(y’+y) + yz’(x’+x) y+y’=1, x+x’=1
= x’z’•1 + yz’•1
= x’z’ + yz’

36. Problem
Minimize the following Boolean expression using Boolean identities −
F(A,B,C)=A′B+BC′+BC+AB′C′
Given F(A,B,C)=A′B+BC′+BC+AB′C′
F(A,B,C)=A′B+B(C′+C)+AB′C′
F(A,B,C)=A’B+B.1+AB’C’
= A’B+B+AB’C’ [B.1=B]
= B(A’+1)+AB’C’ [A’+1=1]
= B+AB’C’ [Apply distributive law A+BC=(A+B)(A+C)]
= (B+B’)(B+AC’) [B+B’=1]
= B+AC’

37. Problem
Minimize the following Boolean expression using Boolean identities −
F(A,B,C)=(A+B)(A+C)
Given, F(A,B,C)=(A+B)(A+C)
F(A,B,C)=A.A+A.C+B.A+B.C
=A+AC+AB+BC [A.A=A]
= A(1+C+B)+BC [1+Anything=1]
= A+BC

39. • Boolean algebra deals with binary variables and logic operation. A Boolean
Function is described by an algebraic expression called Boolean
expression which consists of binary variables, the constants 0 and 1, and the logic
operation symbols. Consider the following example.
Here the left side of the equation represents the output Y. So we can state equation
no. 1
Boolean Expression ⁄ Function

40. •A truth table represents a table having all combinations of inputs and their
corresponding result.
•It is possible to convert the switching equation into a truth table. For example,
consider the following switching equation.
•The output will be high (1) if A = 1 or BC = 1 or both are 1. The truth table for this
equation is shown by Table (a). The number of rows in the truth table is 2n
where
n is the number of input variables (n=3 for the given equation). Hence there are
23
= 8 possible input combination of inputs.
Truth Table Formation

42. •It is in the form of sum of three terms AB, AC, BC with each individual term is a
product of two variables. Say A.B or A.C etc. Therefore such expressions are
known as expression in SOP form.
•The sum and products in SOP form are not the actual additions or multiplications.
In fact they are the OR and AND functions.
•In SOP form, 0 represents a bar and 1 represents an unbar. SOP form is
represented by Given below is an example of SOP.
Sum of Products (SOP) Form