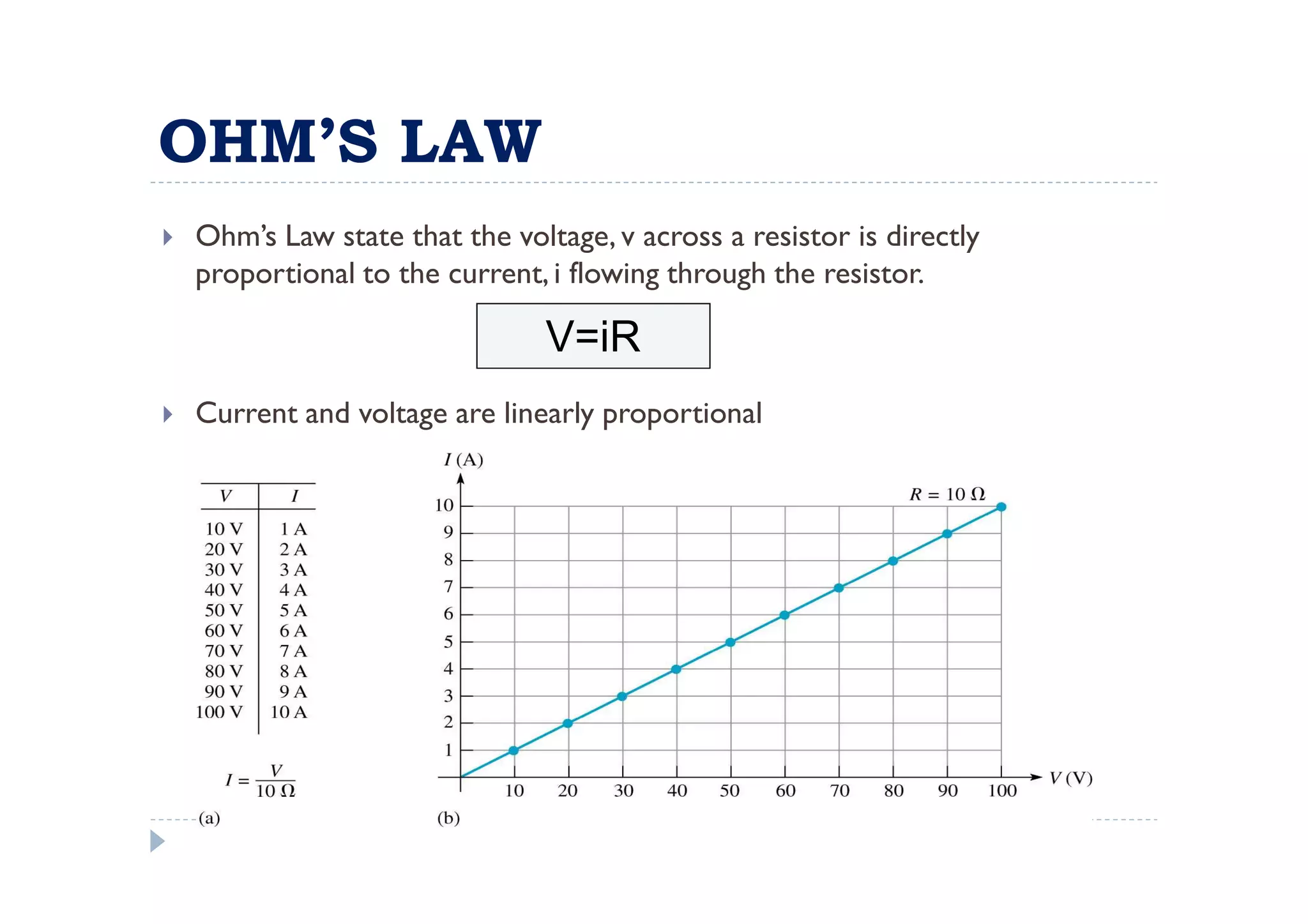
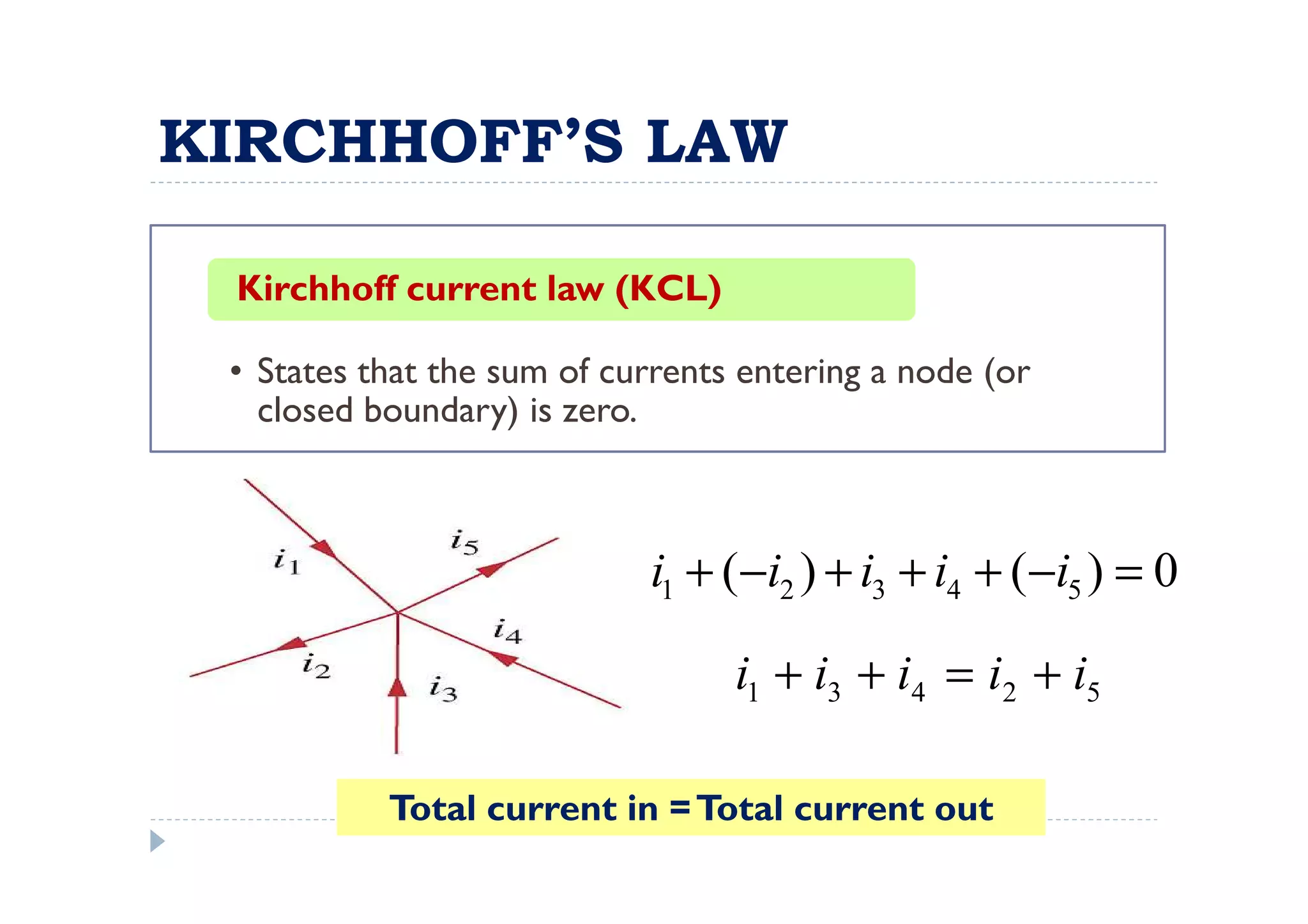
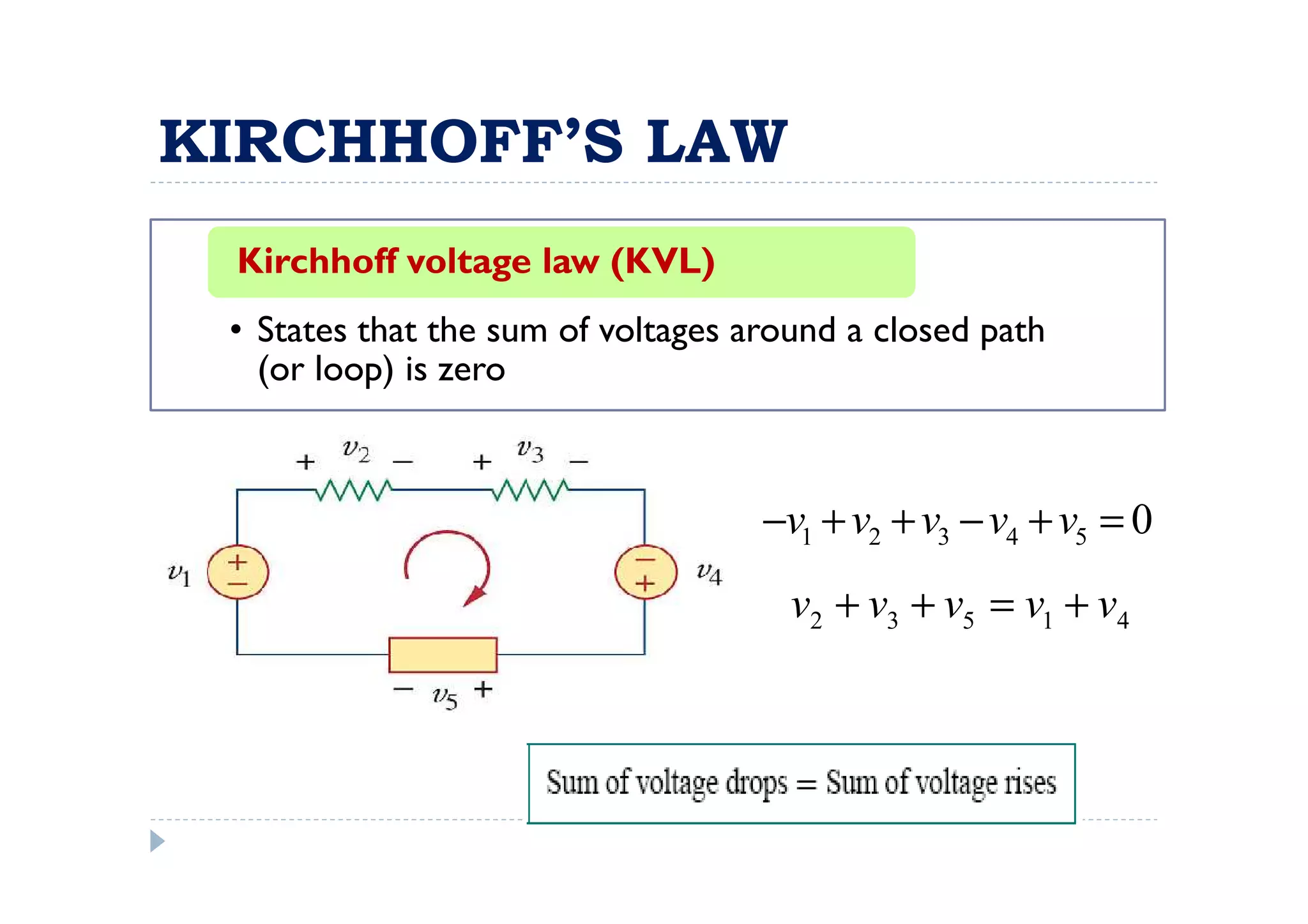
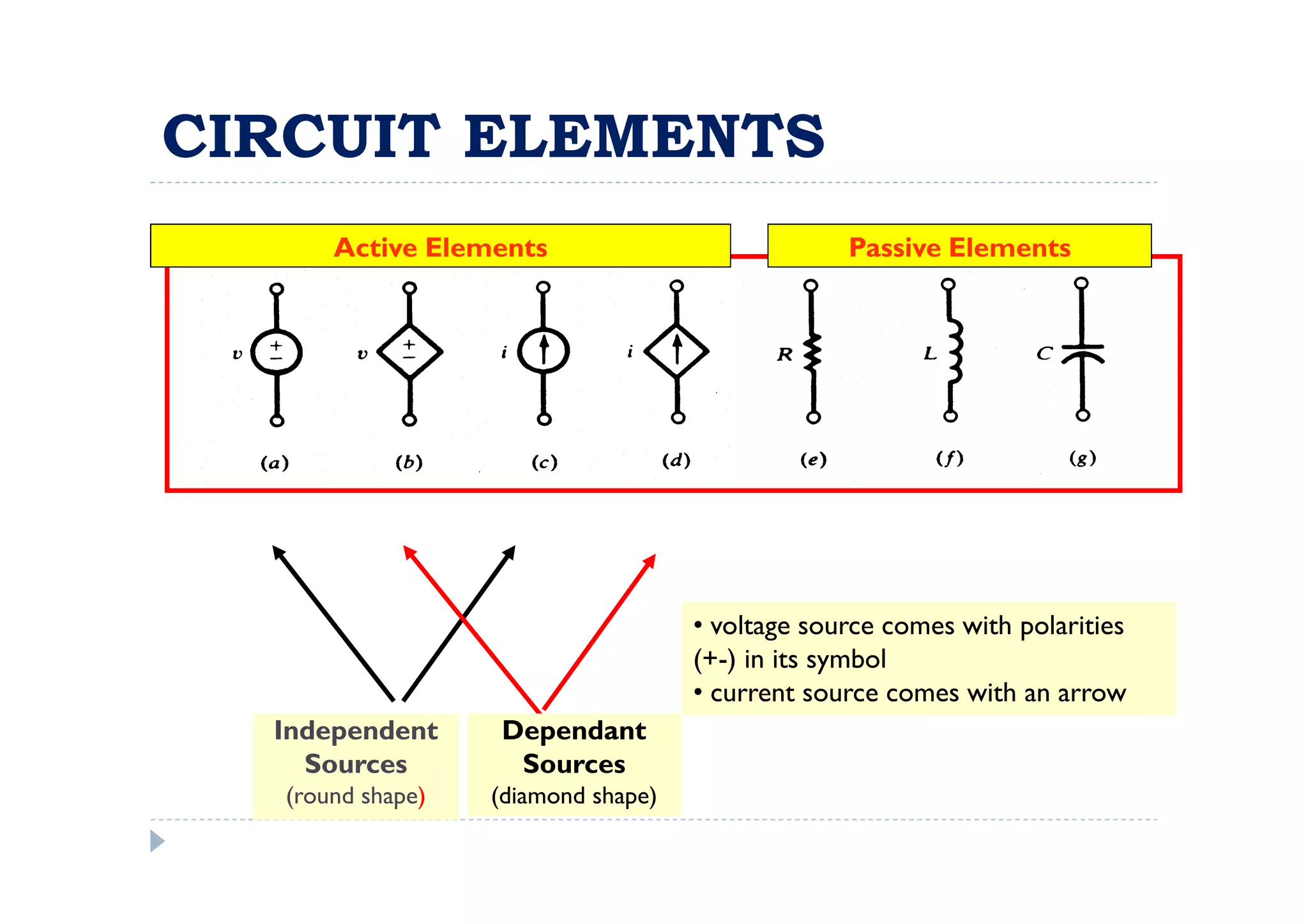
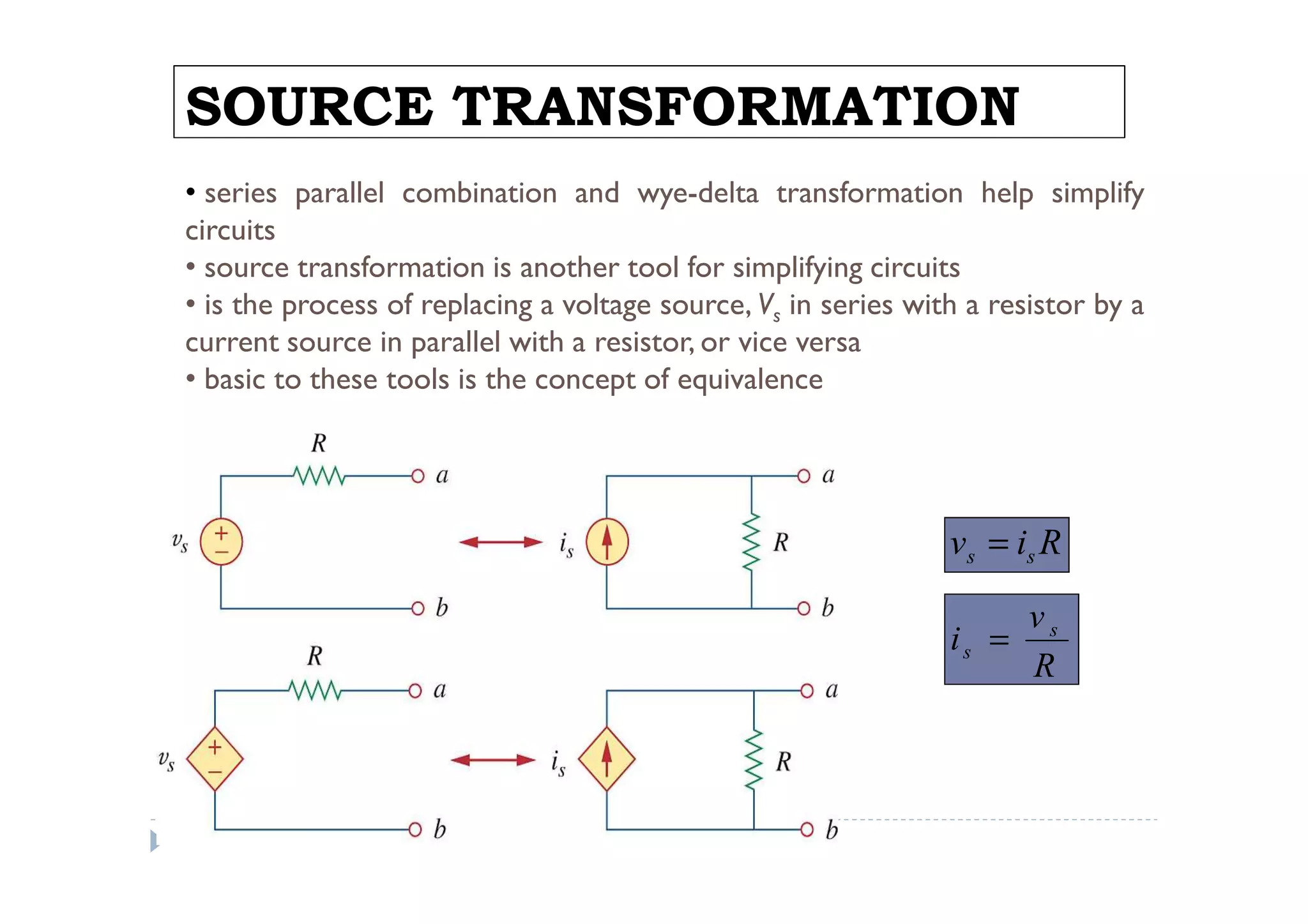
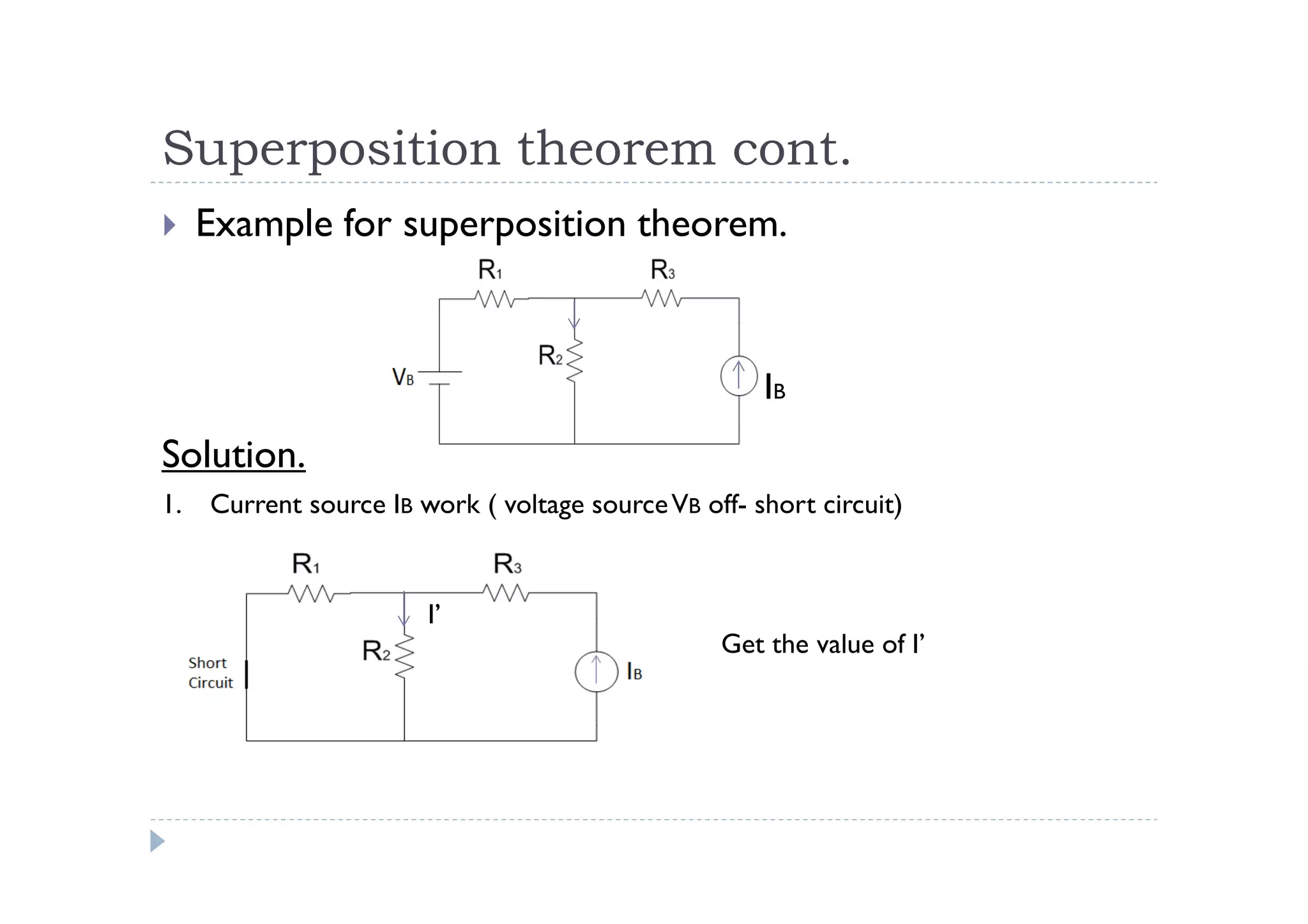
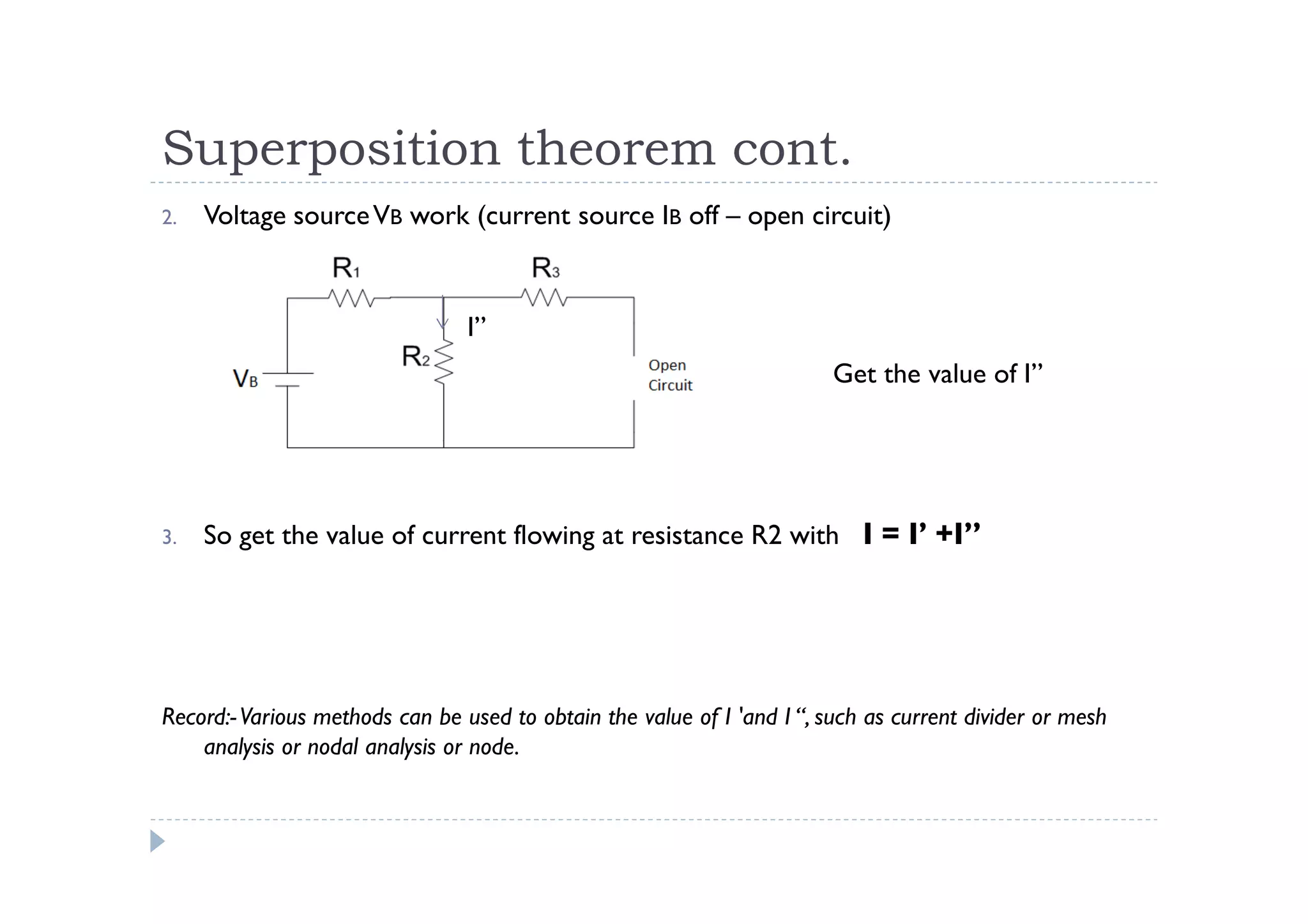
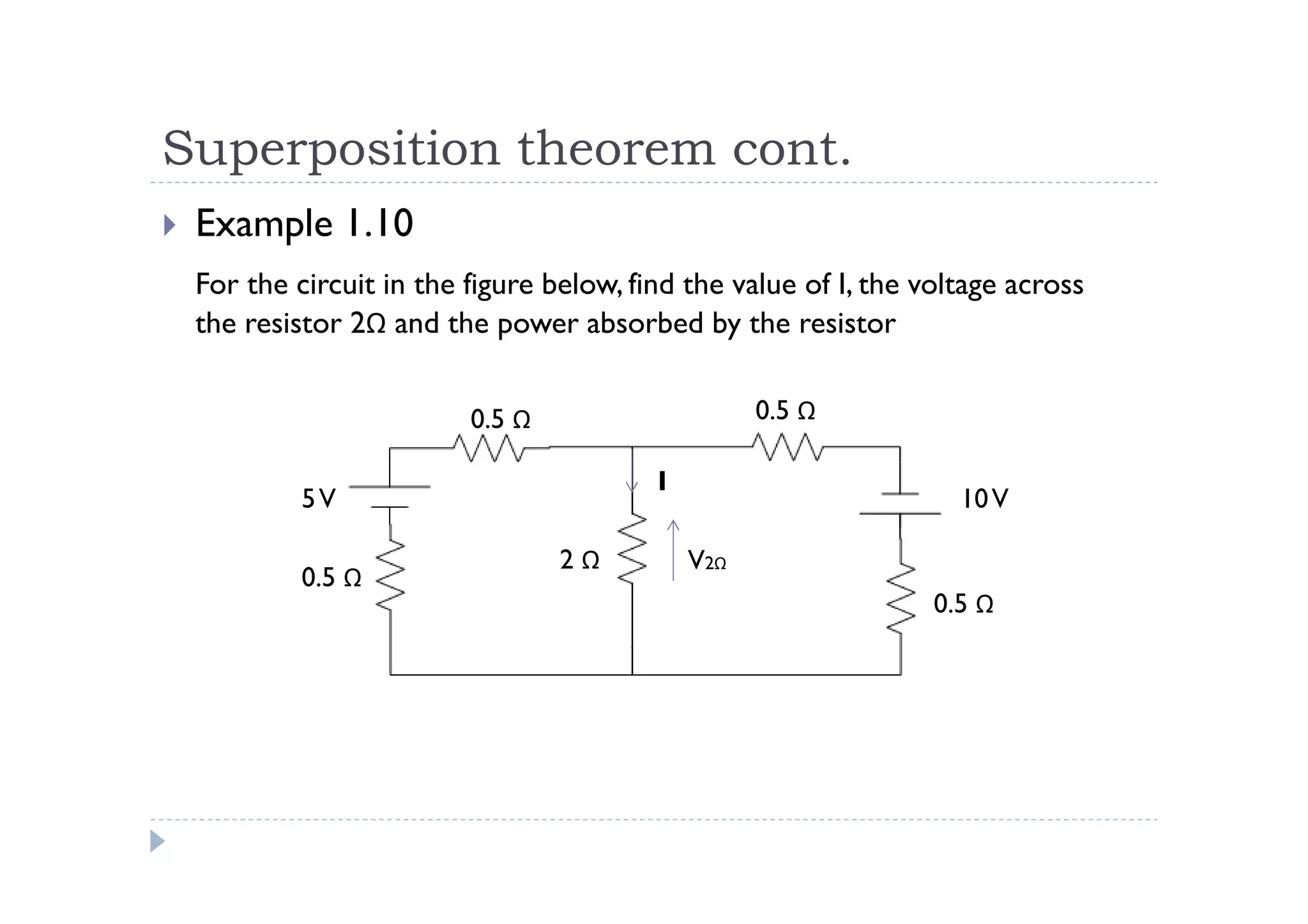
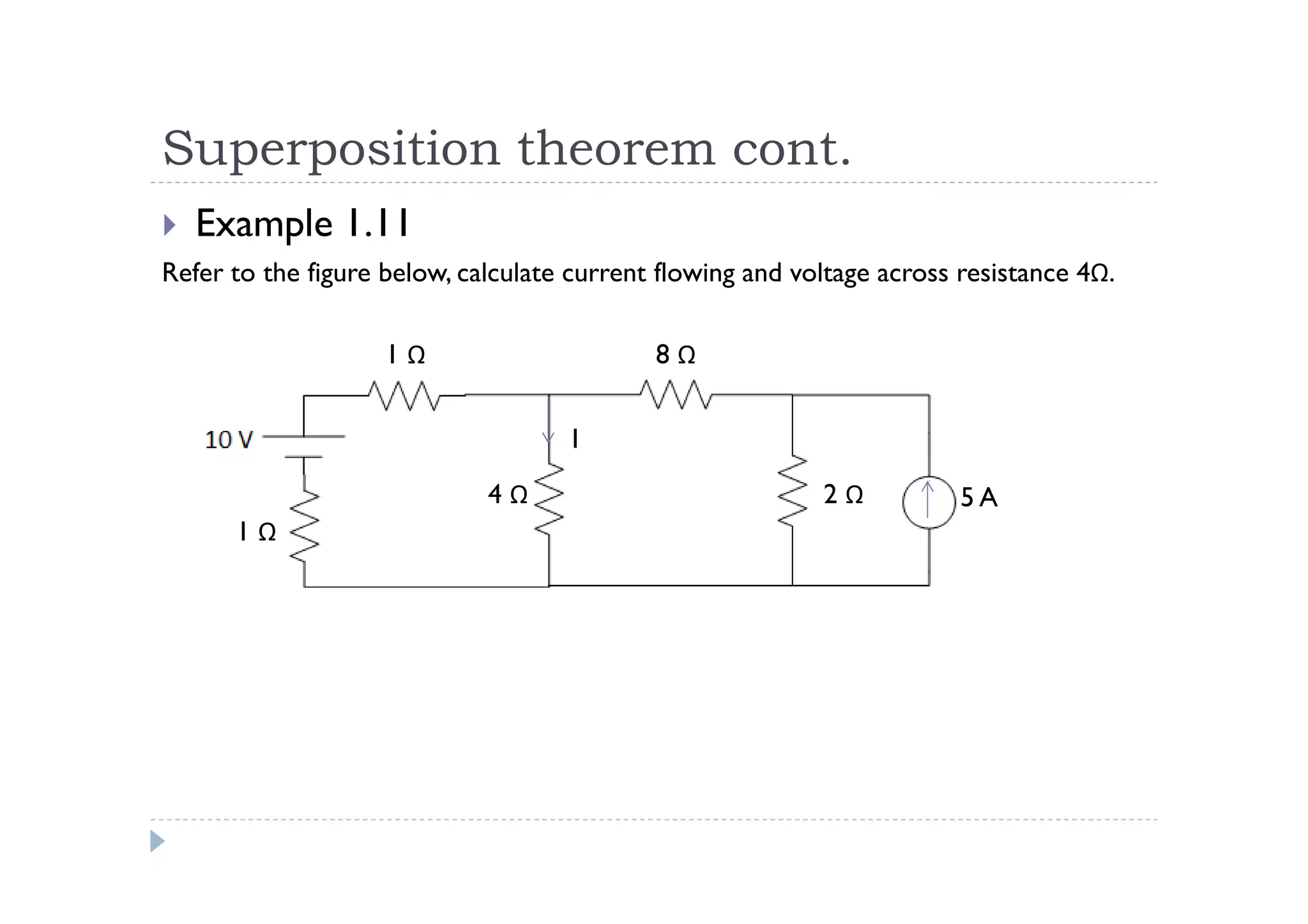
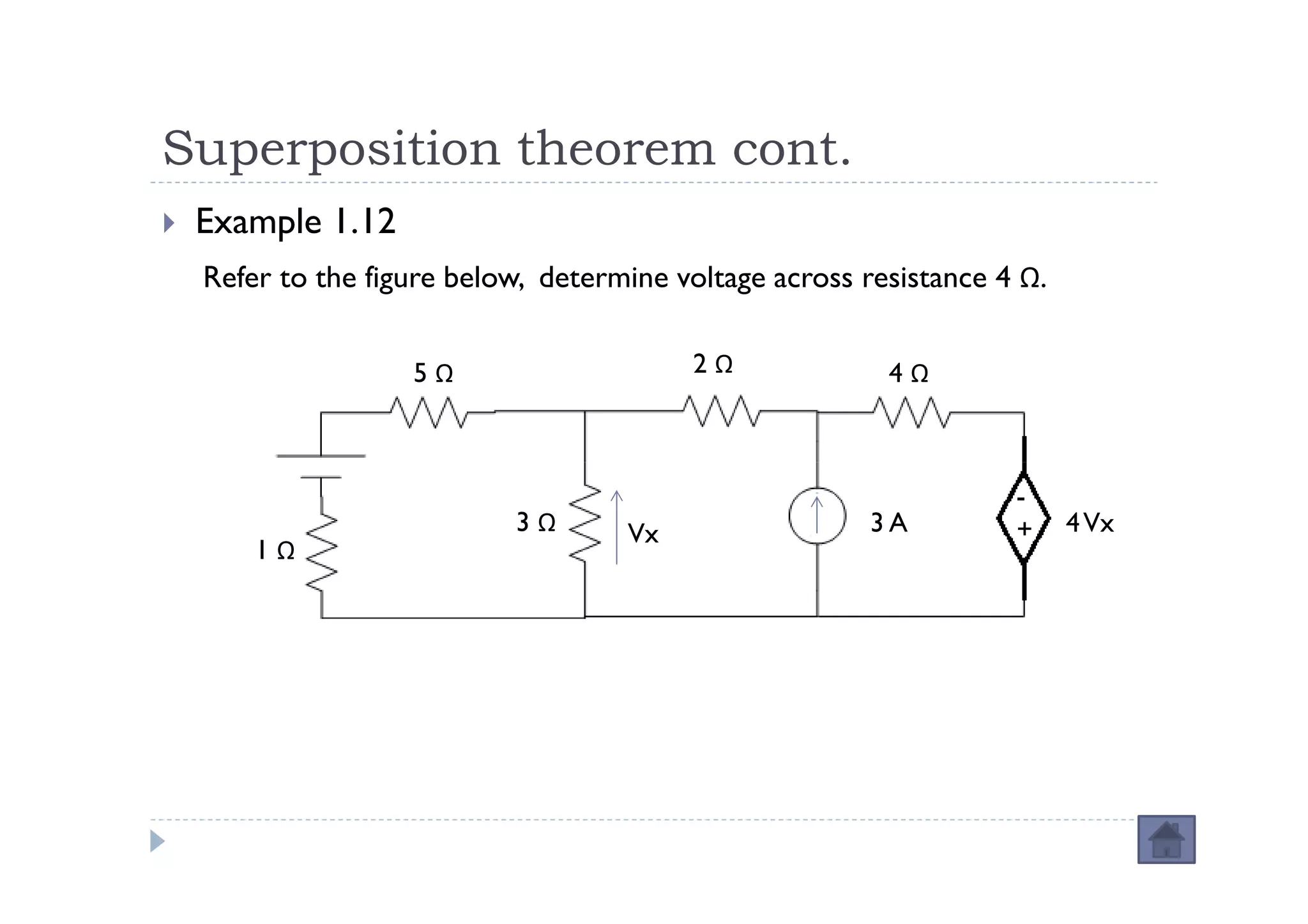
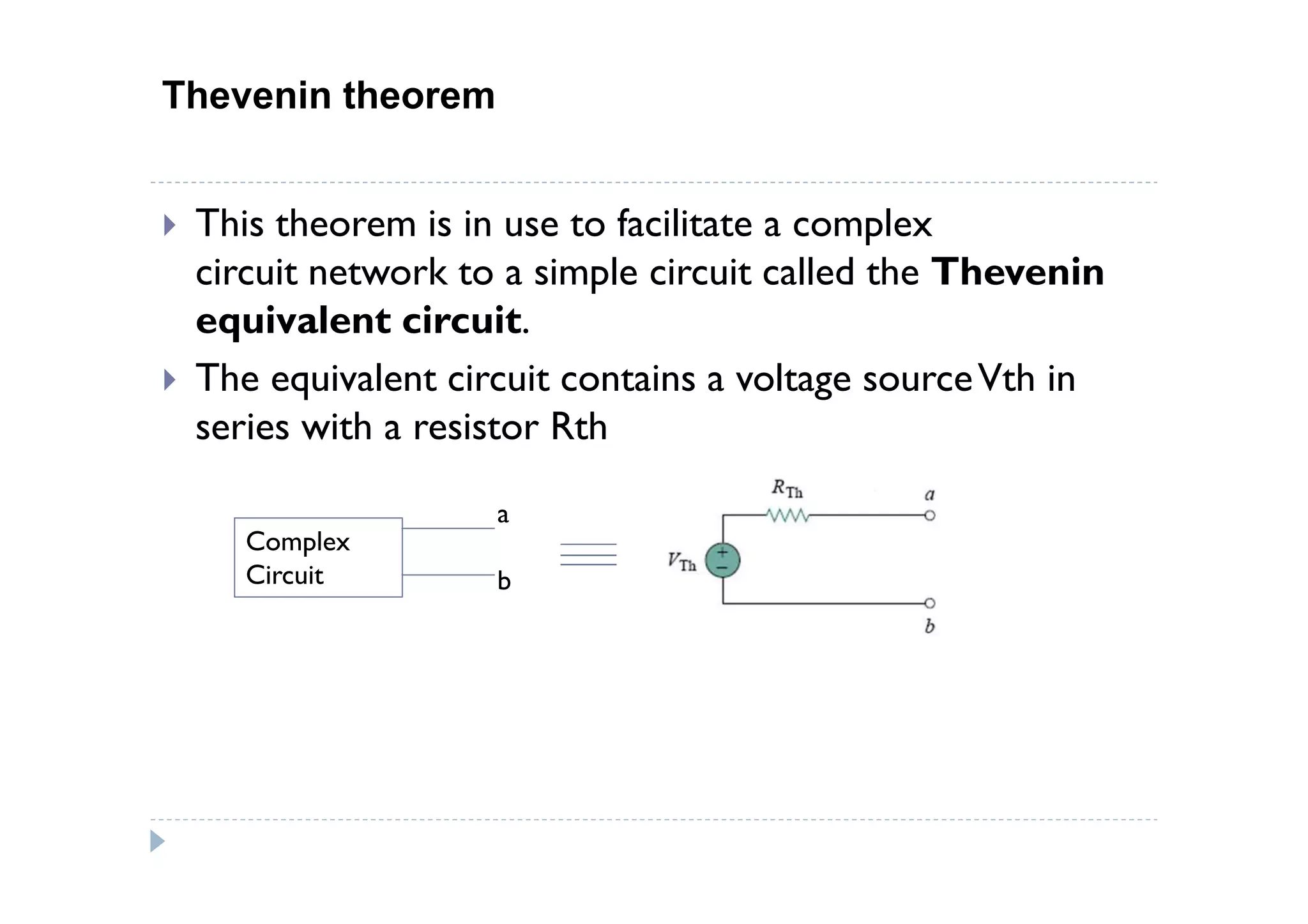
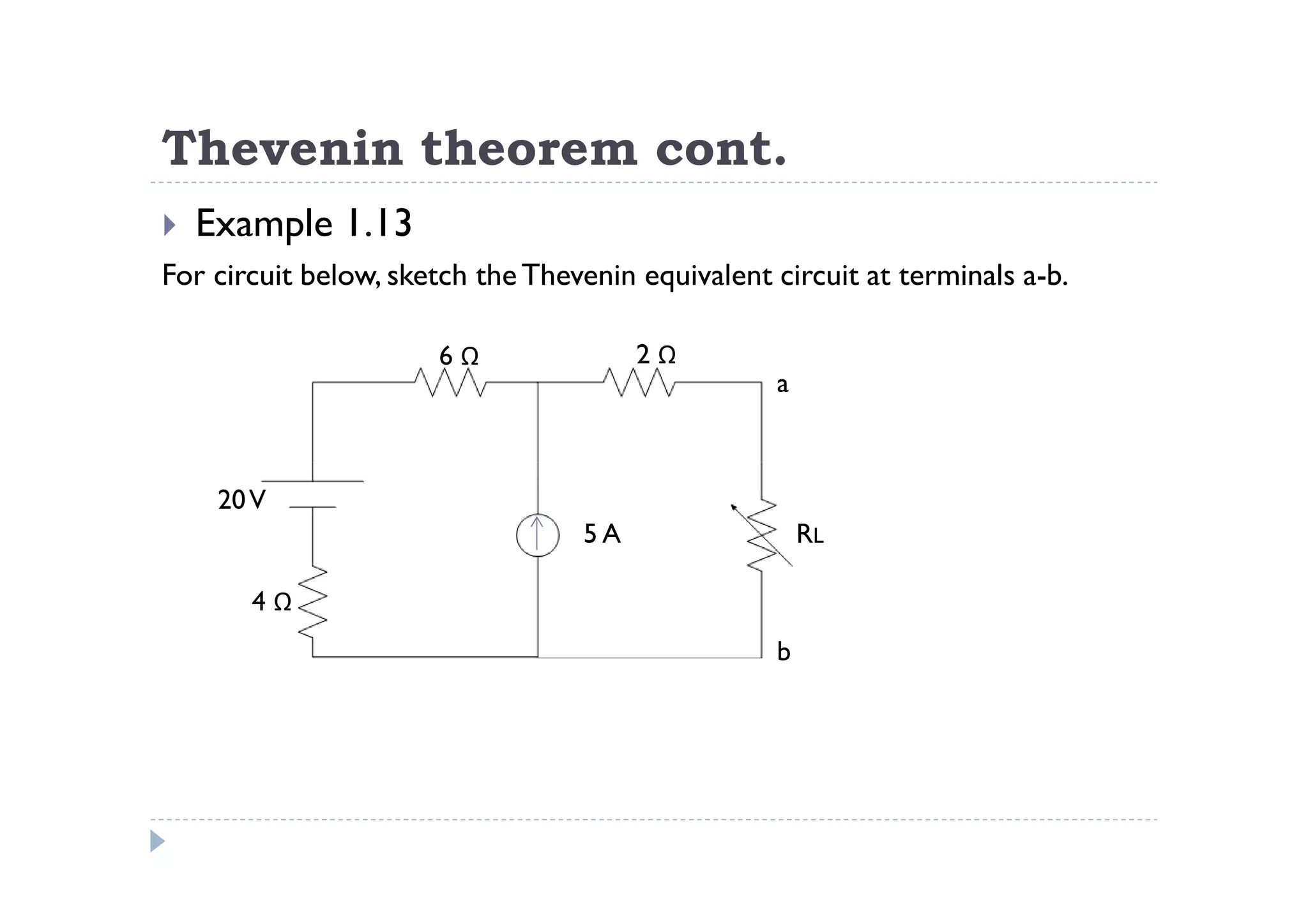
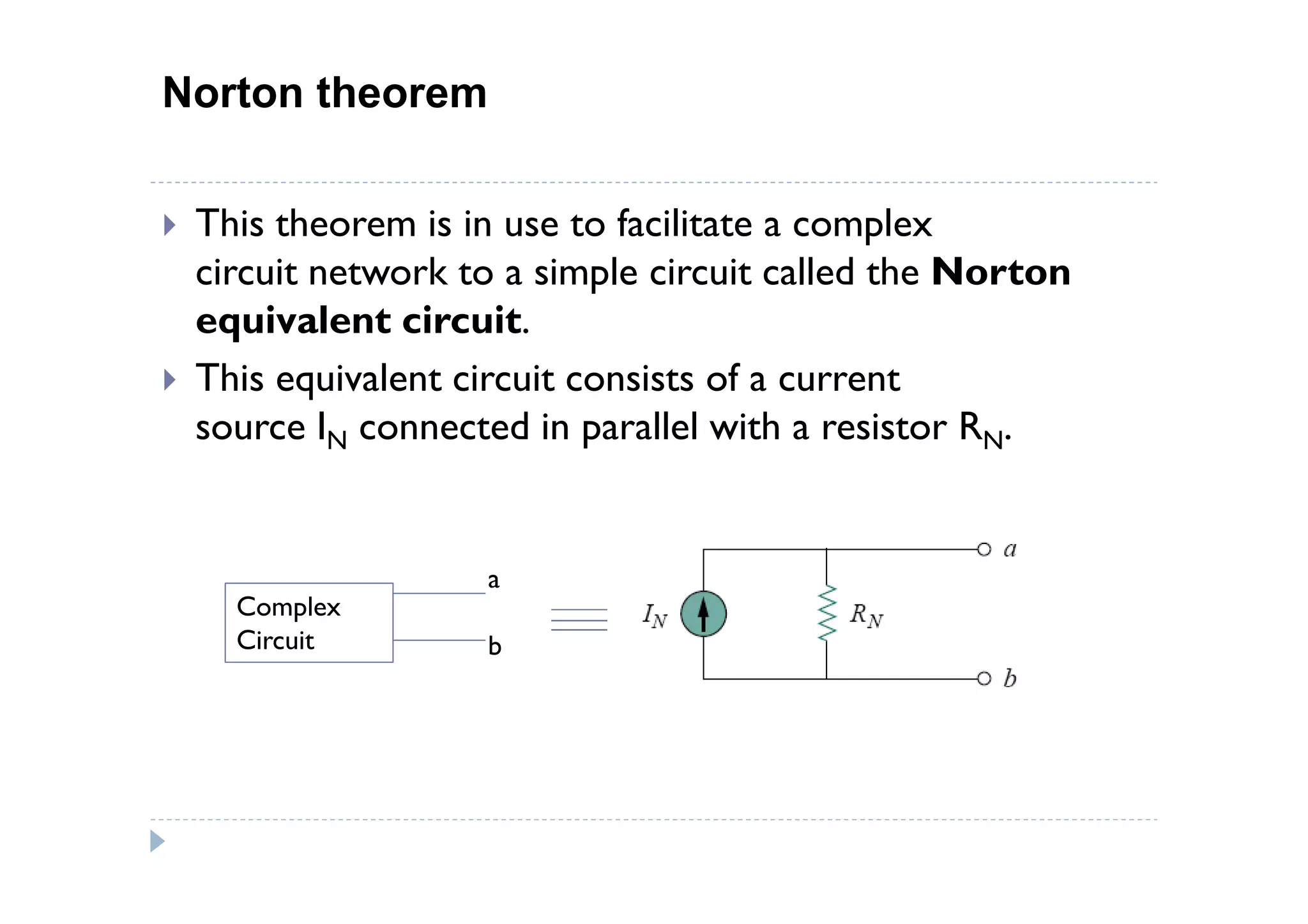
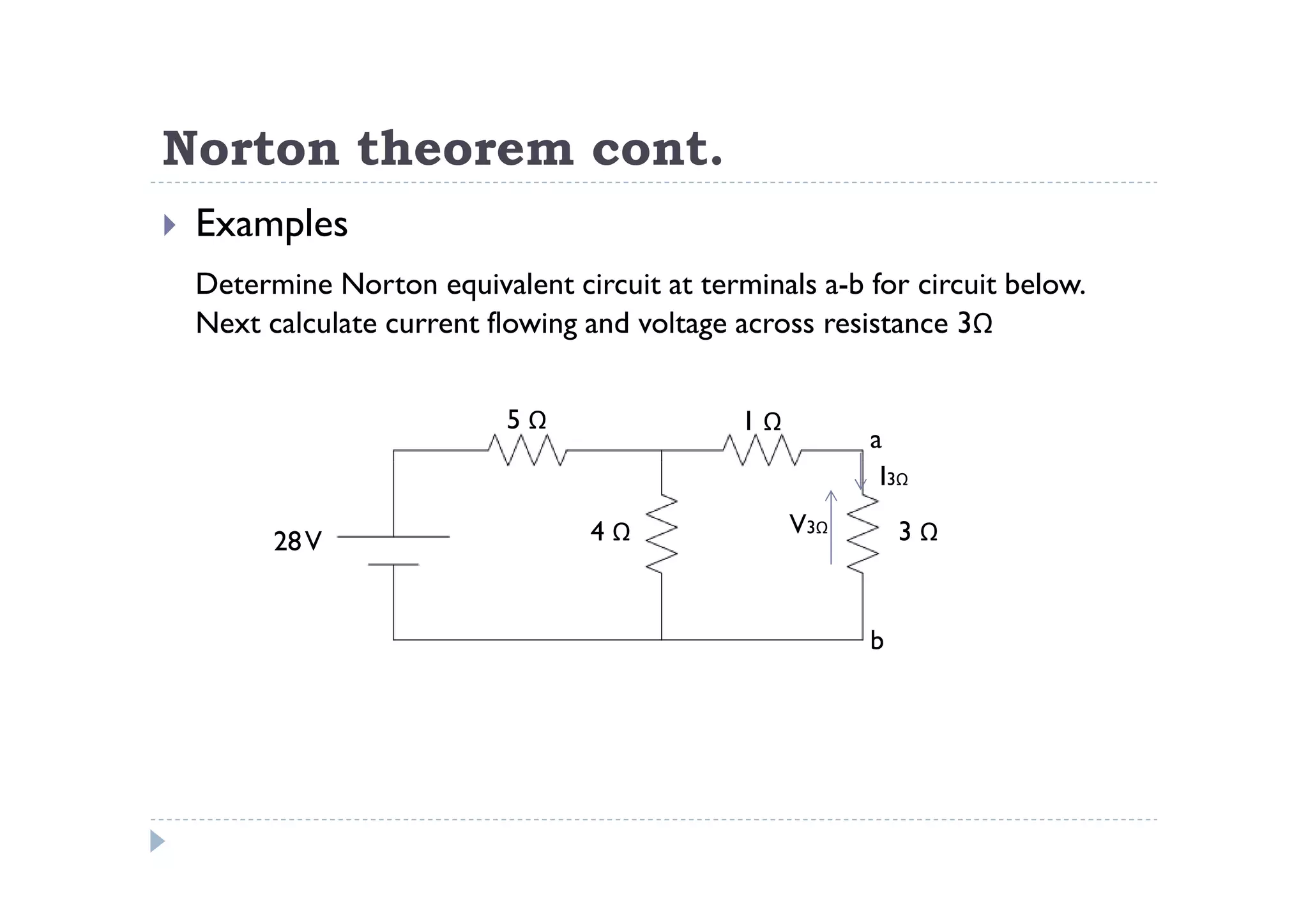
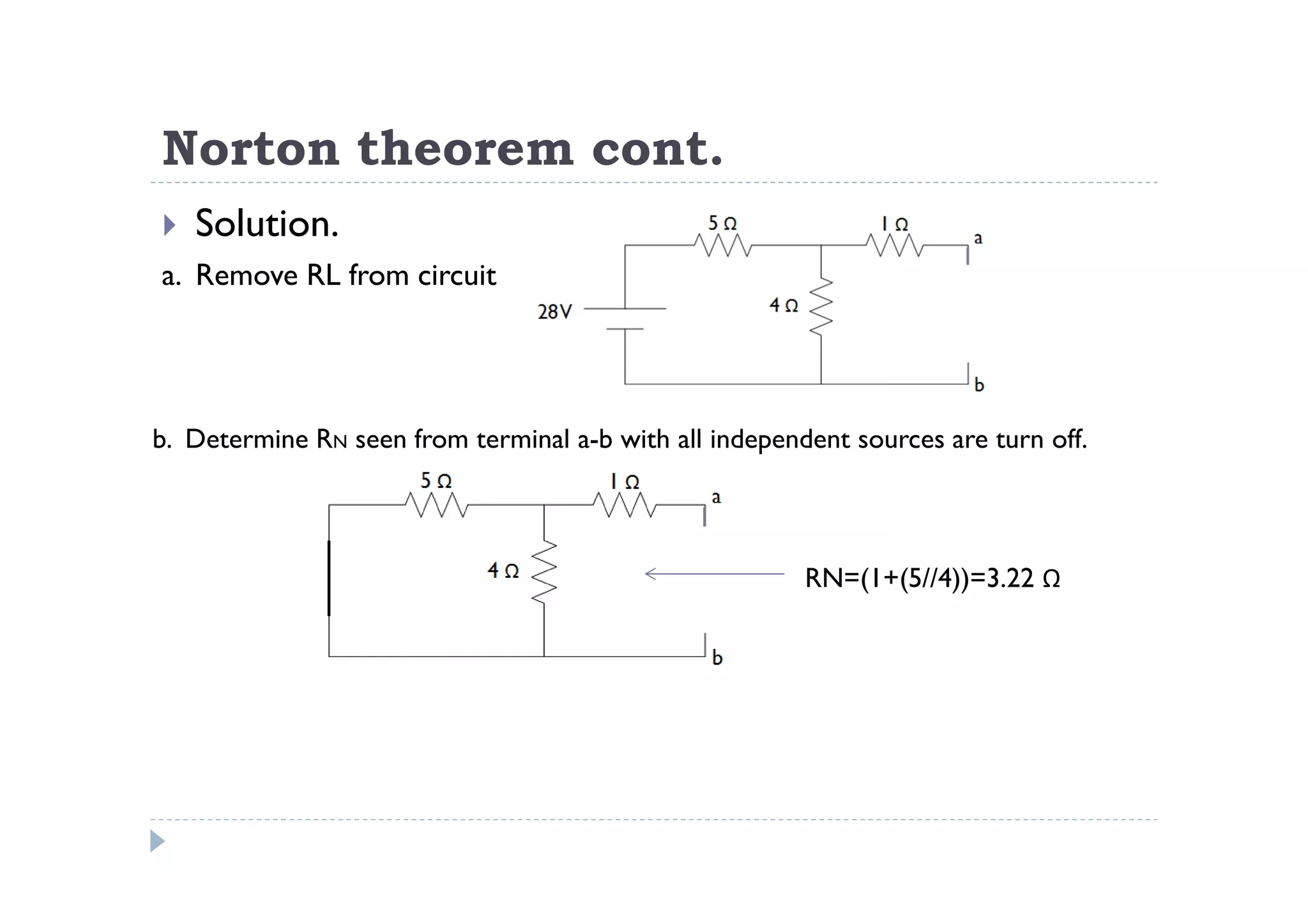
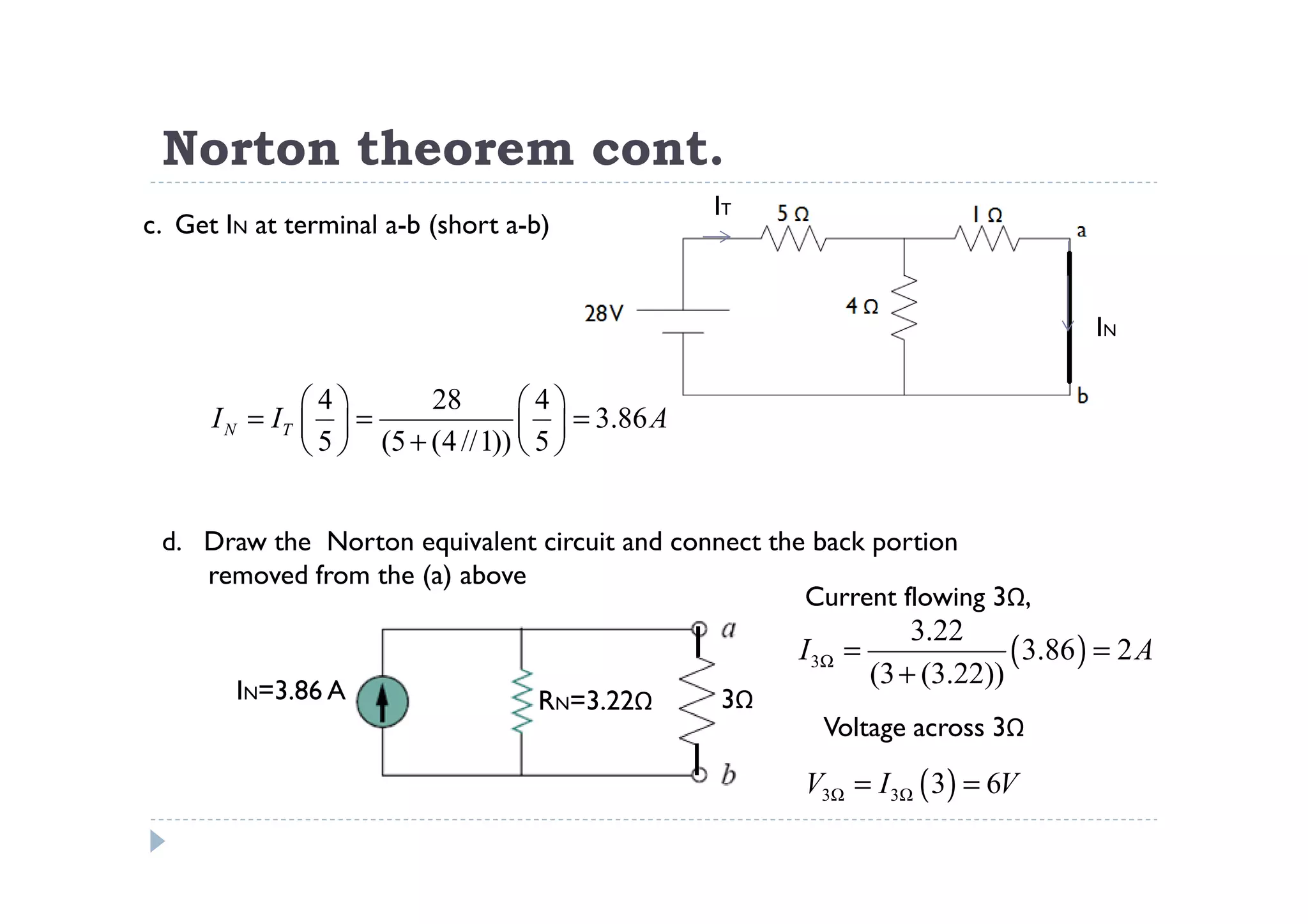
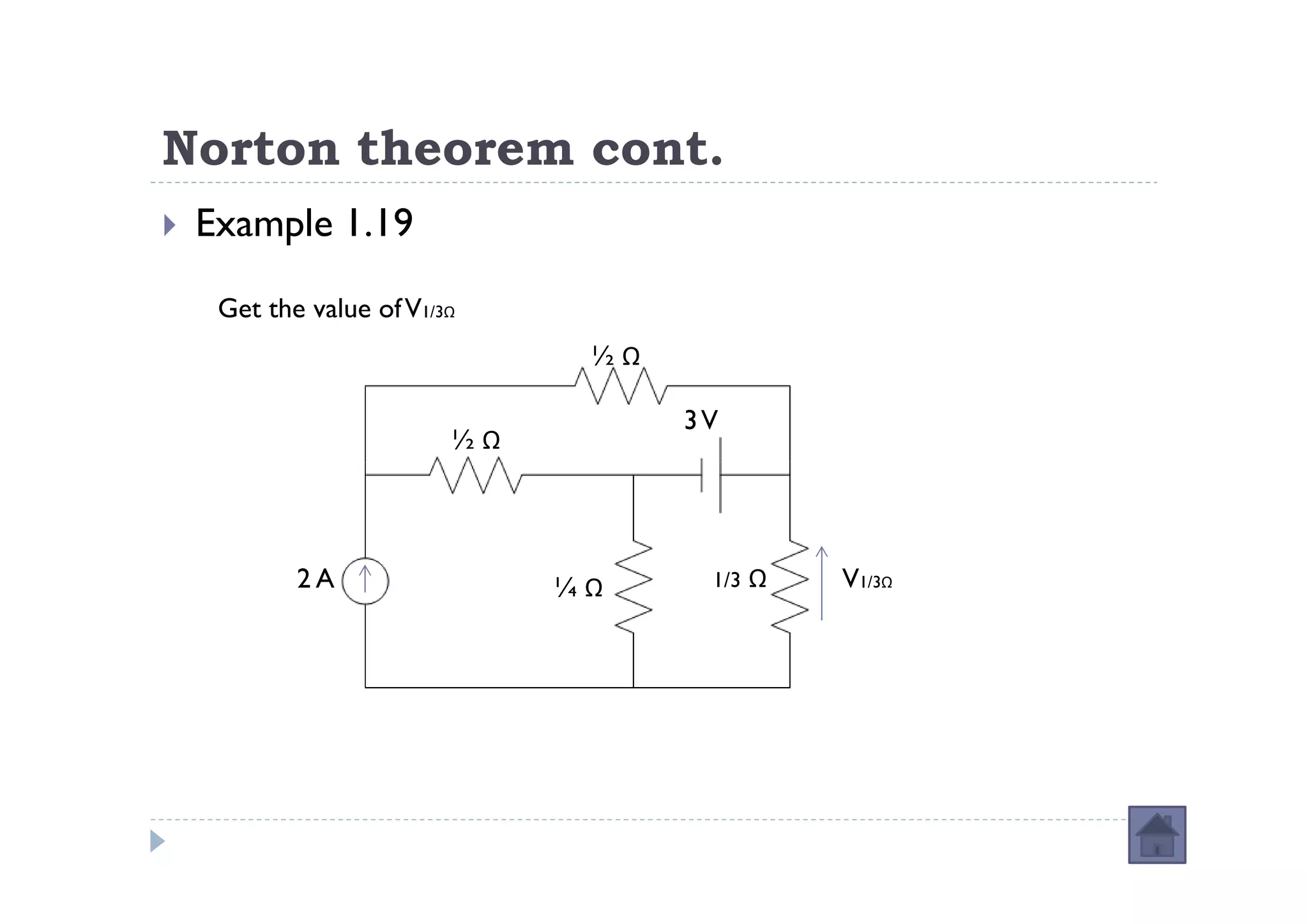
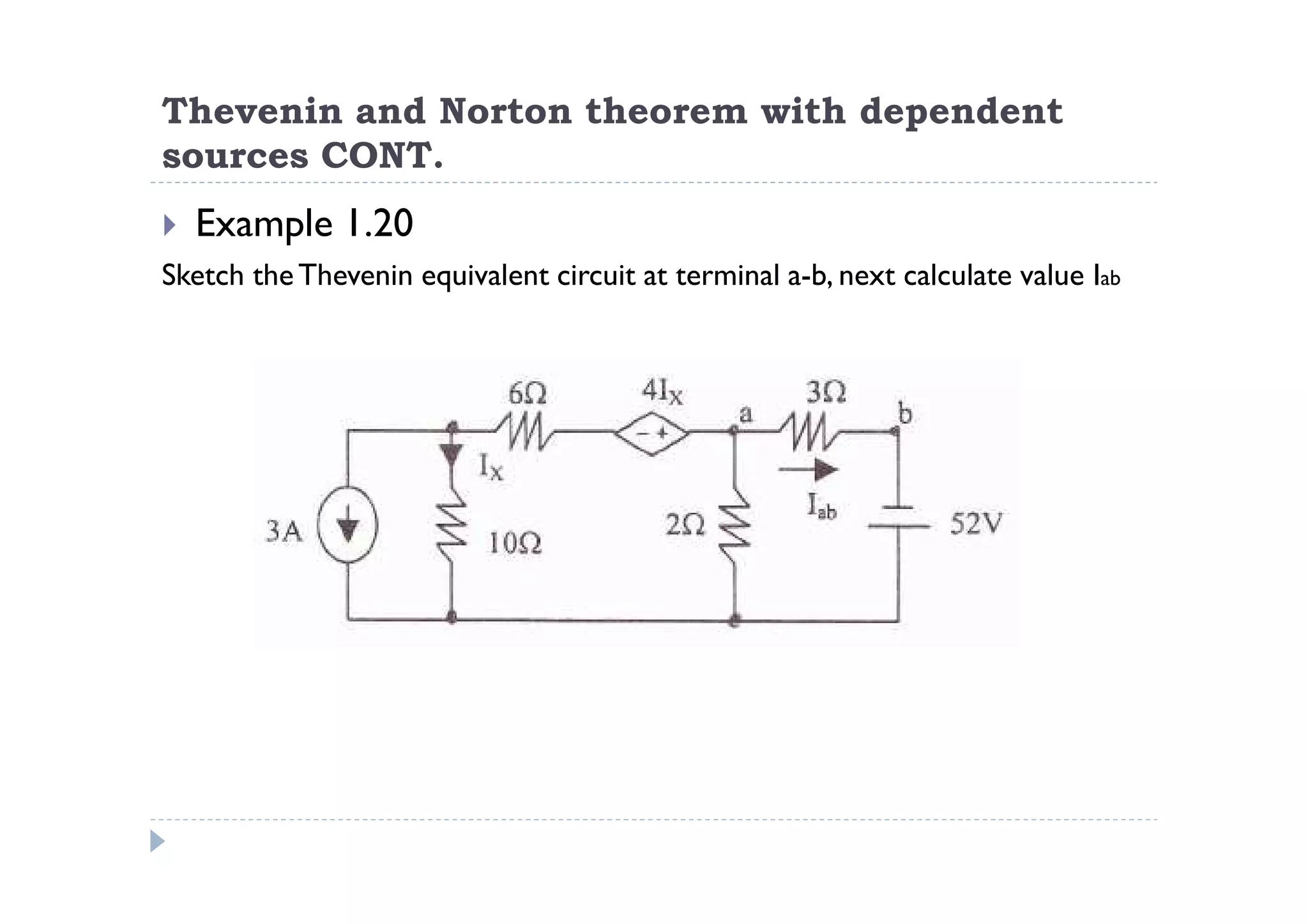
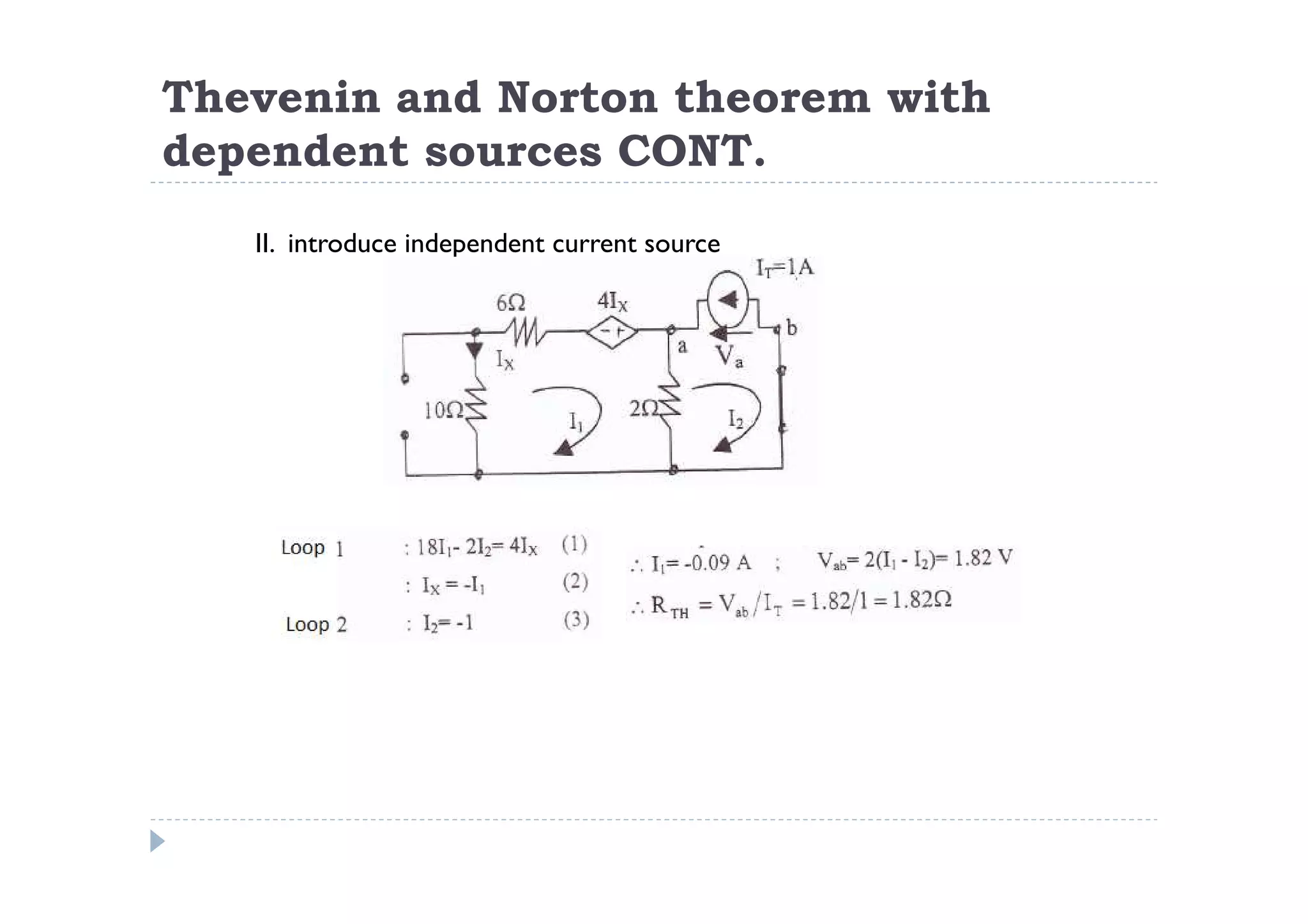
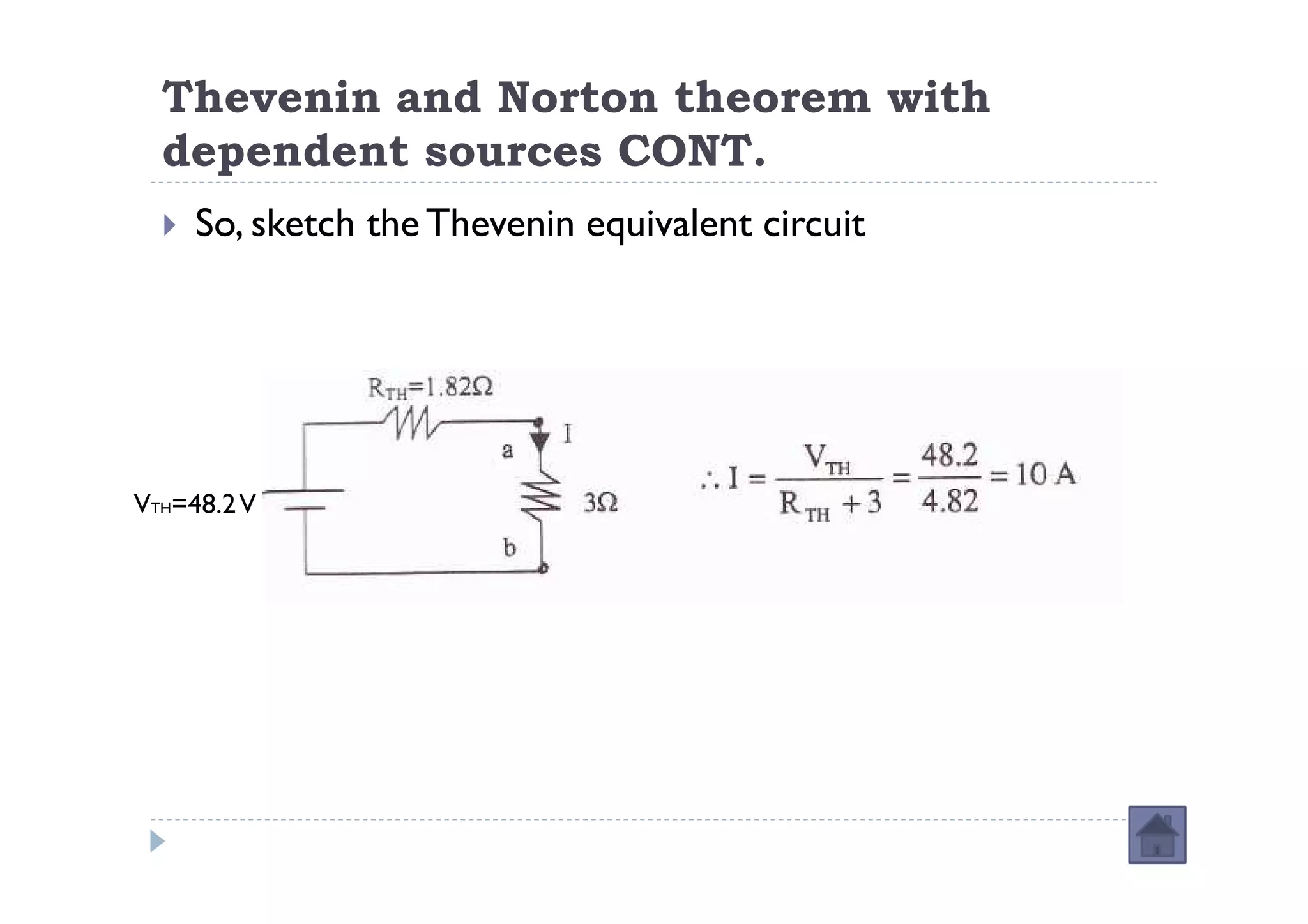
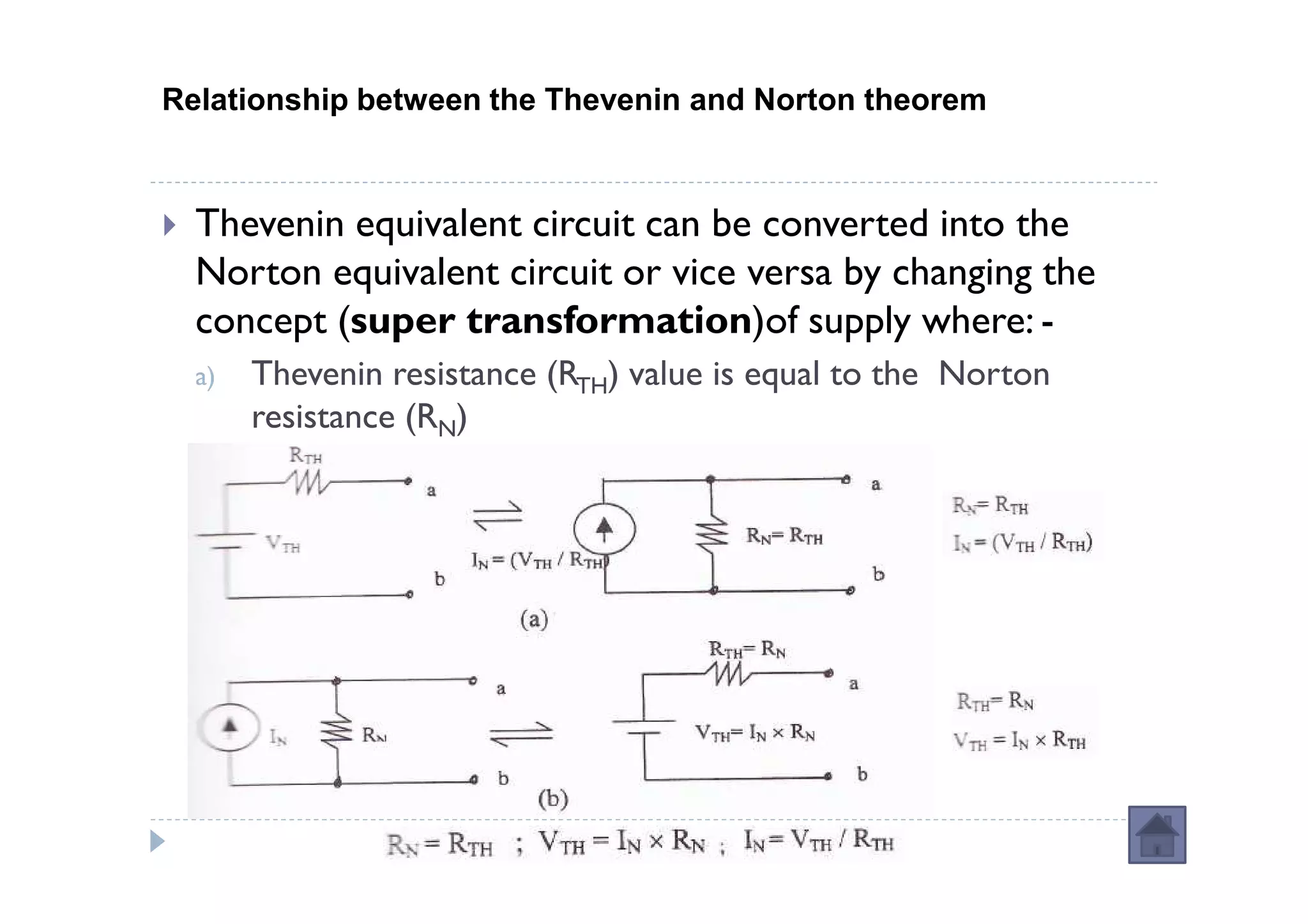
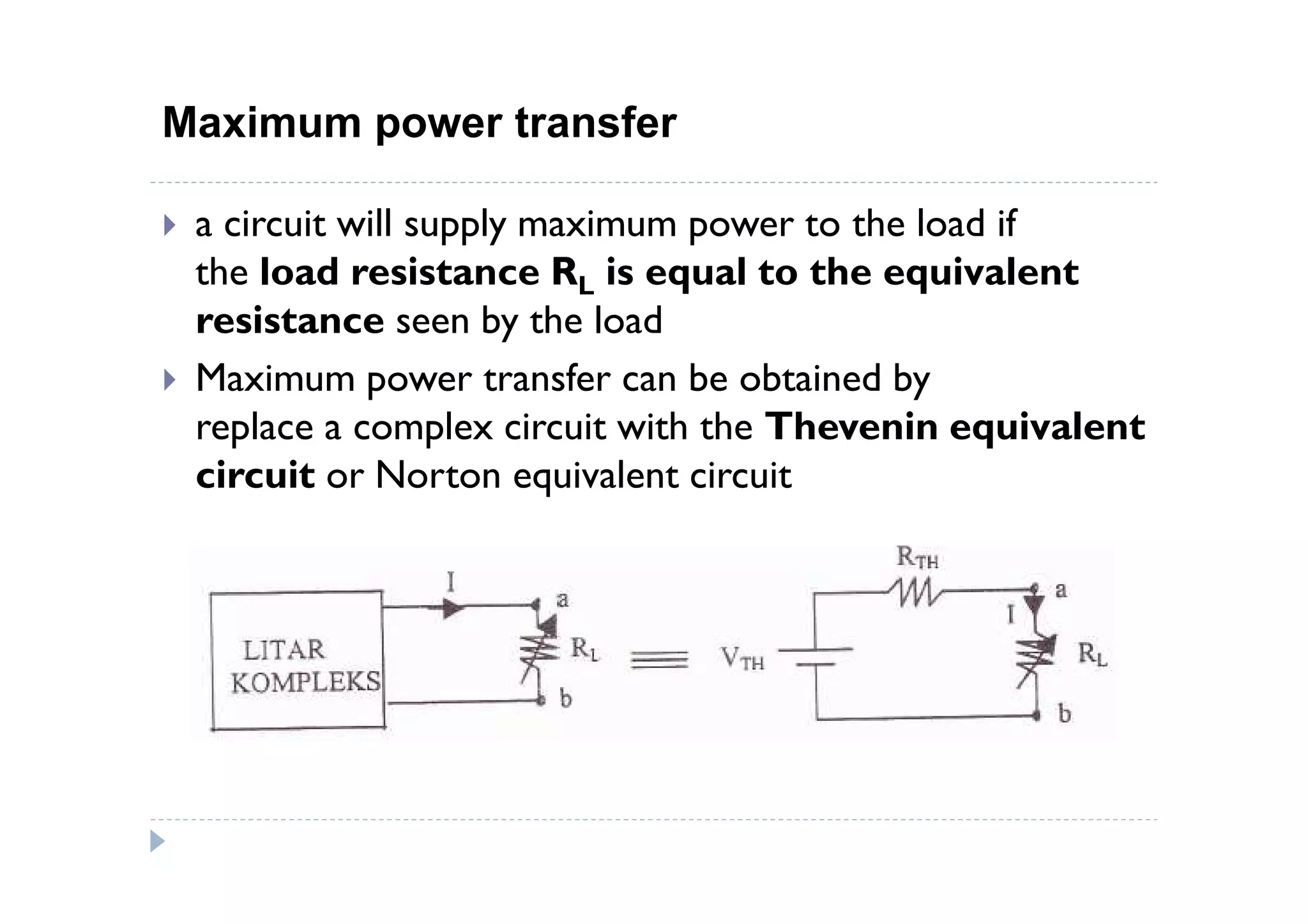
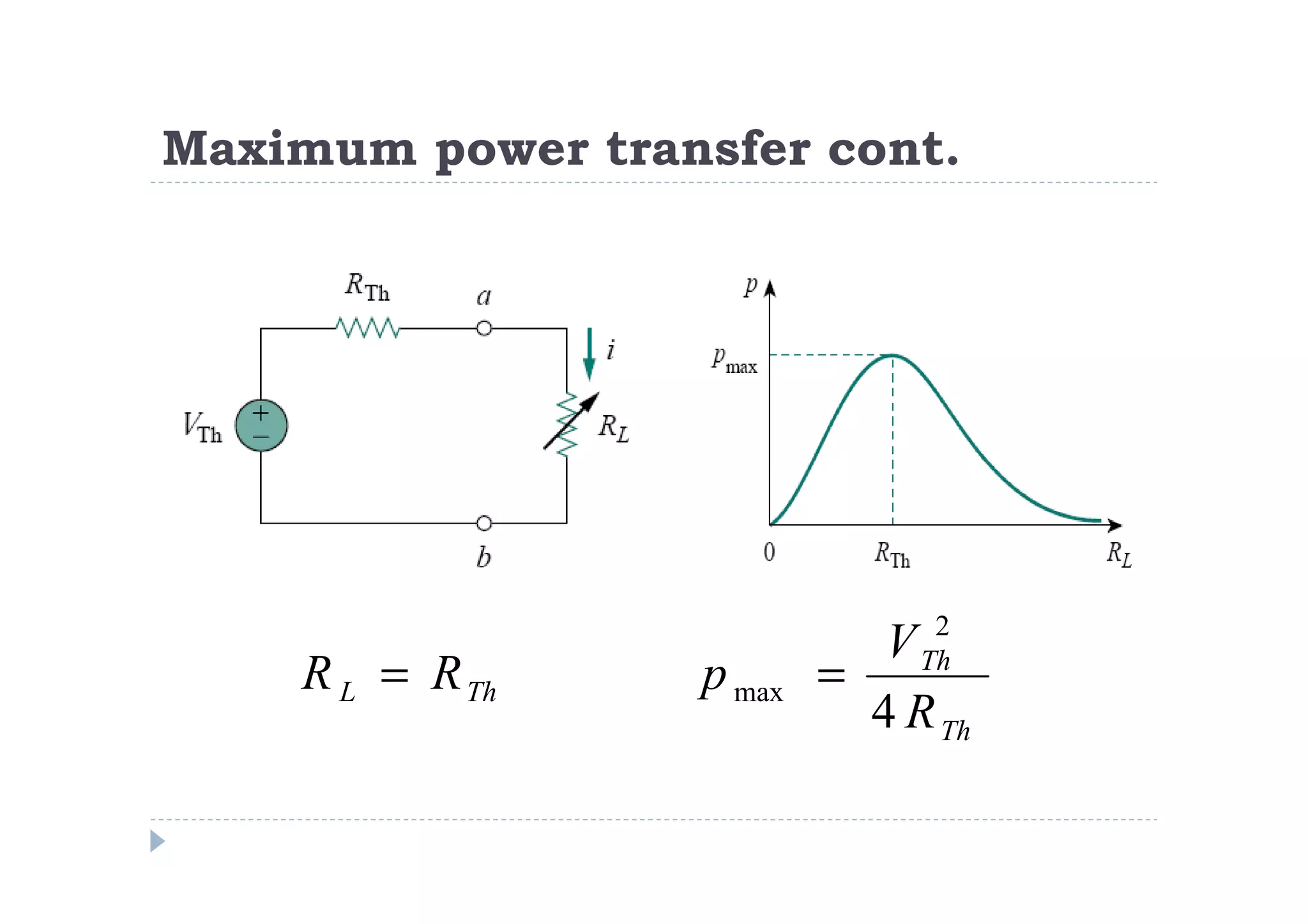
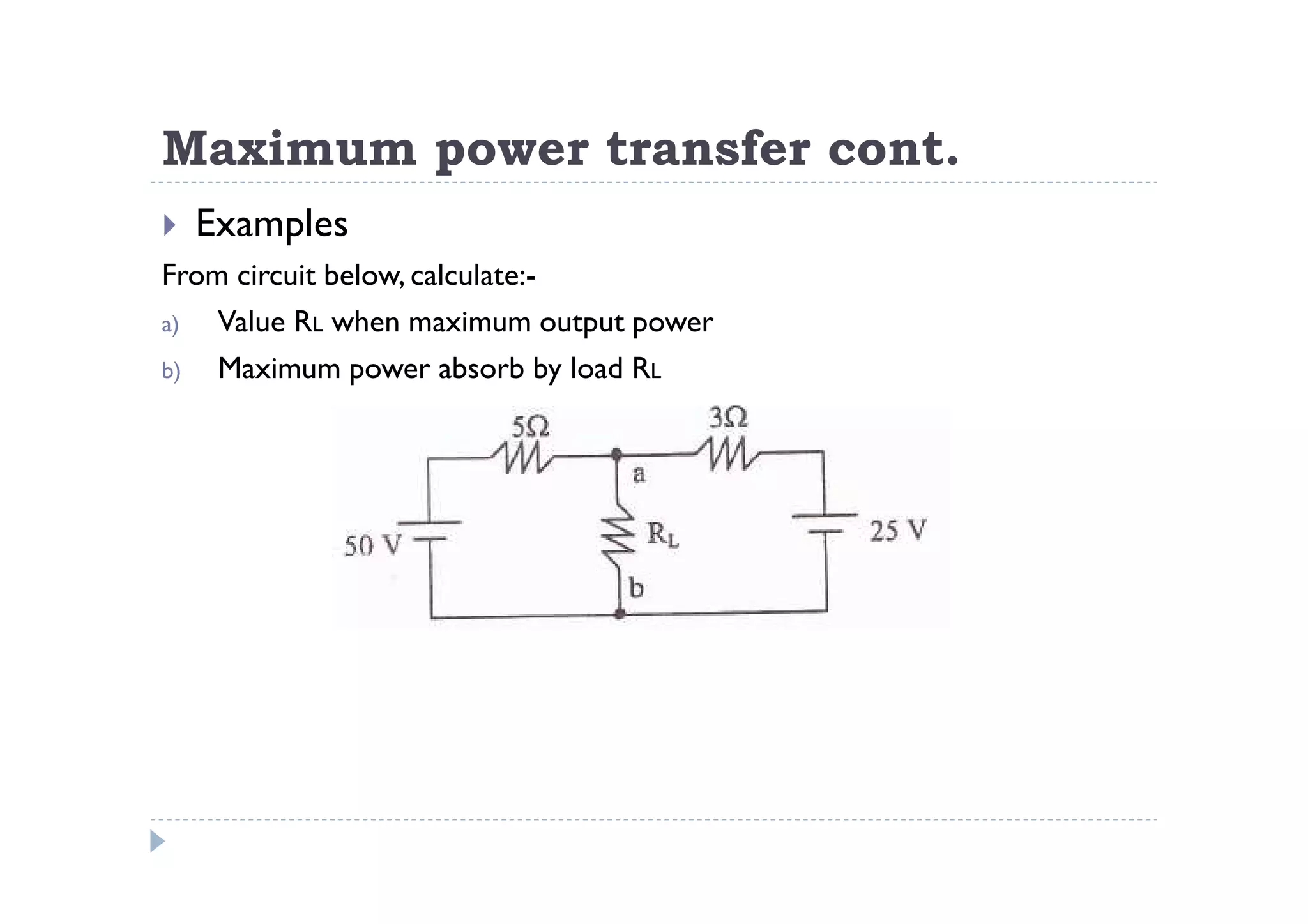
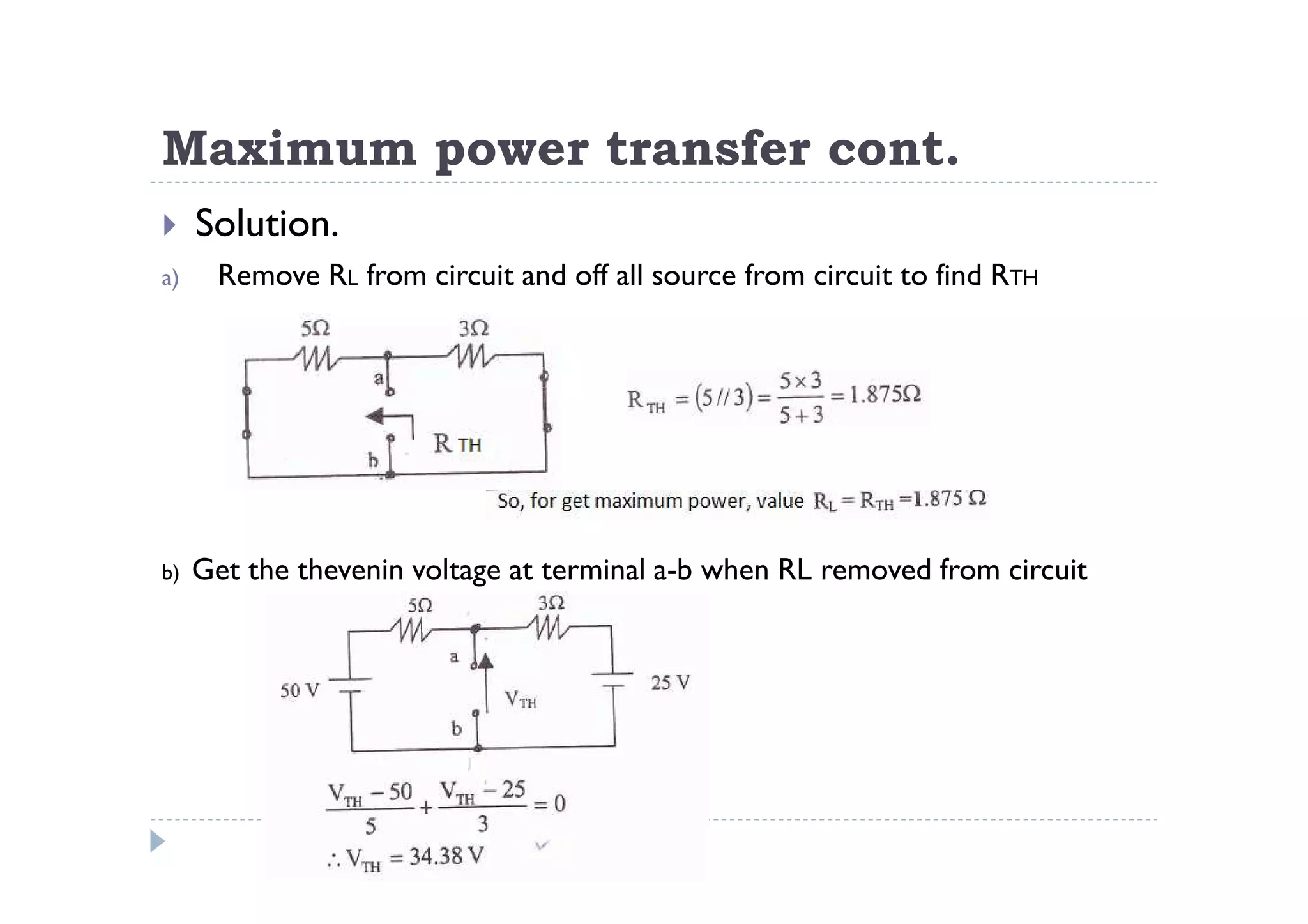
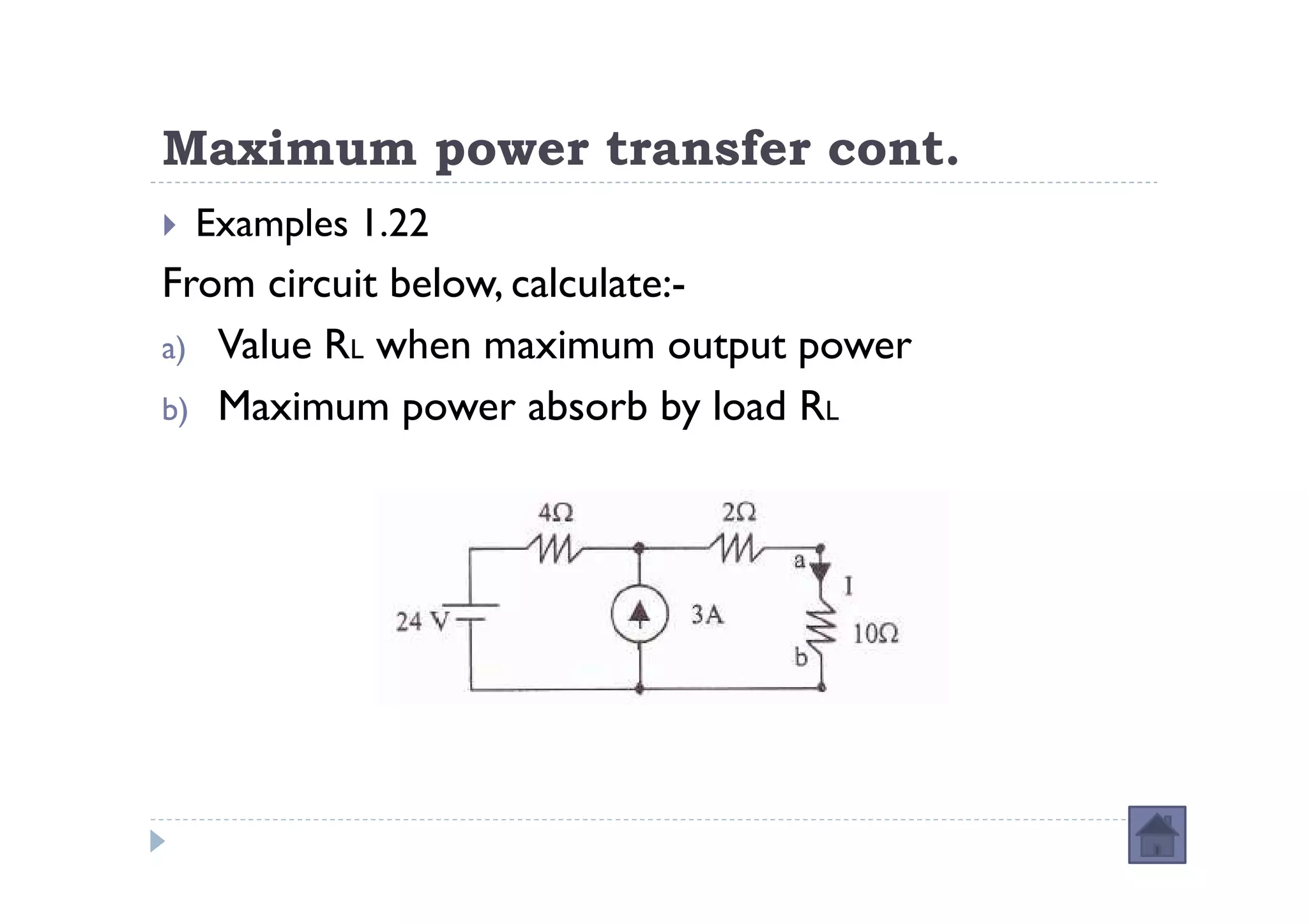
Menuntut ilmu adalah TAQWA - Seeking knowledge is piety. Menyampaikan ilmu adalah IBADAH - Conveying knowledge is worship. Mengulang-ulang ilmu adalah ZIKIR - Repeating knowledge is remembrance of God. Mencari ilmu adalah JIHAD - Seeking knowledge is jihad.

1. Menuntut ilmu adalah TAQWA
Menyampaikan ilmu adalah IBADAH
Mengulang-ulang ilmu adalah ZIKIR
Mencari ilmu adalah JIHAD
Chapter 1 : Techniques of DC Circuit
Analysis
Engr. Mohd Riduwan bin Ghazali (Grad. IEM)

2. 1.1 Review Circuit Analysis I:
Most Important thing that should remember:
Ohm Laws,V = IR
(Kirchoff’s) KCL/KVL
Independent/Dependent Source
Nodal/SuperNode
Mesh/SuperMesh
Source Transformation

3. OHM’S LAW
Ohm’s Law state that the voltage, v across a resistor is directly
proportional to the current, i flowing through the resistor.
V=iR
Current and voltage are linearly proportional

4. KIRCHHOFF’S LAW
Kirchhoff current law (KCL)
• States that the sum of currents entering a node (or
closed boundary) is zero.
i1 + (−i2 ) + i3 + i4 + ( −i5 ) = 0
i1 + i3 + i4 = i2 + i5
Total current in = Total current out

5. KIRCHHOFF’S LAW
Kirchhoff voltage law (KVL)
• States that the sum of voltages around a closed path
(or loop) is zero
−v1 + v2 + v3 − v4 + v5 = 0
v2 + v3 + v5 = v1 + v4

6. CIRCUIT ELEMENTS
Active Elements Passive Elements
• voltage source comes with polarities
(+-) in its symbol
• current source comes with an arrow
Independent Dependant
Sources Sources
(round shape) (diamond shape)

7. NODAL ANALYSIS
Provides a general procedure for analyzing circuits using node voltages
as the circuit variables.
• Steps:
i) select a node as a reference node (ground)
ii) assign voltage designations to nonreference nodes
iii) redraw the circuit to avoid too much information on the
same circuit
iv) apply KCL for each nonreference node
- at node 1: I1 = I2 + i1 + i2 -at node 2: I2 = i3 – i2
v) apply Ohm’s law (current flows from a higher potential to a lower potential)
vhigher − vlower v1 − 0 v1 − v2 v2 − 0
i= i1 = i2 = i3 =
R R1 R2 R3

8. Nodal Analysis With Voltage Sources
We now consider how voltage sources affect nodal analysis:
CASE 1: If a voltage source is connected between the reference node, we
simply set the voltage at the nonreference node equal to the voltage of the
voltage source
E.g.: v1 = 10V
CASE 2: If the voltage source (dependent or independent) is connected
between two nonreference nodes, the two nonreference nodes form a
generalized node or supernode; apply both KCL and KVL to determine
the node voltages
E.g.: nodes 2 and 3 form a supernode

9. MESH ANALYSIS
Steps to determine mesh currents
• assign mesh currents i1, i2,,…..,in to the n meshes
• apply KVL to each of the n meshes. Use Ohm’s law to express the
voltages in terms of the mesh currents
• solve the resulting simultaneous equations to get the mesh
currents
A p p l y i n g K V L t o m e s h 1,
− V 1 + R 1 i1 + R 3 ( i1 − i 2 ) = 0
( R 1 + R 3 ) i1 − R 3 i 2 = V 1
A p p ly in g K V L to m e s h 2 ,
R 2 i 2 + V 2 + R 3 ( i 2 − i1 ) = 0
− R 3 i1 + ( R 2 + R 3 ) i 2 = − V 2
R1+ R3 − R3  i1   V1 
 − R3 R2 + R3 i  = −V 
  2  2

10. MESH ANALYSIS WITH CURRENT SOURCES
CASE 1
When a current source exists only in one mesh, we set i2 = -5A
and write a mesh equation for the other mesh in the usual way:
-10 + 4i1 + 6(i1 – i2) = 0 i1 = -2A

11. MESH ANALYSIS WITH CURRENT SOURCES
CASE 2
When a current source exists between two meshes, we create a supermesh
by excluding the current source and any elements connected in series with
it
Applying KVL in (b),
-20 + 6i1 + 10i2 + 4i2 = 0 6i1 + 14i2 = 20 ………..(i)
Applying KCL to a node where the two meshes intersect,
i2 = i1 + 6 ………… (ii)
Solve (i) and (ii), i1 = -3.2 A, i2 = 2.8A

12. SOURCE TRANSFORMATION
• series parallel combination and wye-delta transformation help simplify
circuits
• source transformation is another tool for simplifying circuits
• is the process of replacing a voltage source, Vs in series with a resistor by a
current source in parallel with a resistor, or vice versa
• basic to these tools is the concept of equivalence
v s = is R
vs
is =
R

13. Superposition theorem
For circuit network have more than one independent
source
voltage or current produced by a source acting in
isolation can be determined by assuming other
sources do not work, where the resources should
be switched off in the following manner: -
Independent voltage source – short circuit (0 V) or internal
resistance if have
Independent current source – open circuit (0 A)

14. Superposition theorem cont.
Example for superposition theorem.
IB
Solution.
1. Current source IB work ( voltage source VB off- short circuit)
I’
Get the value of I’

15. Superposition theorem cont.
2. Voltage source VB work (current source IB off – open circuit)
I”
Get the value of I”
3. So get the value of current flowing at resistance R2 with I = I’ +I”
Record:- Various methods can be used to obtain the value of I 'and I “, such as current divider or mesh
analysis or nodal analysis or node.

16. Superposition theorem cont.
Example 1.10
For the circuit in the figure below, find the value of I, the voltage across
the resistor 2Ω and the power absorbed by the resistor
0.5 Ω 0.5 Ω
I
5V 10 V
2Ω V2Ω
0.5 Ω
0.5 Ω

17. Superposition theorem cont.
Solution
1. Voltage source 5V work ( voltage source 10 V off – short circuit)
Find the value of I’ RT = 1 + ( 2 //1) = 1.67Ω
 5 
IT =   = 3A
 1.67 
1
I'= xIT = 1A
2 +1

18. Superposition theorem cont.
2. Voltage source 10 V work ( voltage source 5 V off – short circuit)
Find the value of I” RT = 1 + ( 2 //1) = 1.67Ω
 10 
IT =   = 6A
 1.67 
1
I"= xIT = 2 A
2 +1
3. So the value of current I (make sure the direction of I’ and I”)
I = I '+ (− I ") = −1A
V2 Ω = IR = (−1)(2) = −2V
P2 Ω = I 2 ( R) = (−1) 2 (2) = 2W

19. Superposition theorem cont.
Example 1.11
Refer to the figure below, calculate current flowing and voltage across resistance 4Ω.
1Ω 8Ω
I
4Ω 2Ω 5A
1Ω

20. Superposition theorem cont.
Example 1.12
Refer to the figure below, determine voltage across resistance 4 Ω.
5Ω 2Ω 4Ω
-
3Ω Vx 3A + 4 Vx
1Ω

21. Thevenin theorem
This theorem is in use to facilitate a complex
circuit network to a simple circuit called the Thevenin
equivalent circuit.
The equivalent circuit contains a voltage source Vth in
series with a resistor Rth
a
Complex
Circuit b

22. Thevenin theorem cont.
I=0 A
a a
Complex OFF
VTH RTH
Circuit b Circuit b
The steps to get the Thevenin equivalent circuit:-
a. Remove section of the network where to find the thevenin
equivalent circuit and mark clearly the two terminals as a-b
b. Determine the Thevenin equivalent resistance seen from the
terminal a-b with independent sources is turn off
c. Get the values of Thevenin voltage on the voltage across the
terminal a-b when the terminal at open circuit. (various method
can be used to obtain Vth, whether to used loop analysis/nod
analysis)
d. Draw the Thevenin equivalent circuit and connect the back portion
removed from the (a) above

23. Thevenin theorem cont.
Example 1.13
For circuit below, sketch the Thevenin equivalent circuit at terminals a-b.
6Ω 2Ω
a
20 V
5A RL
4Ω
b

24. Thevenin theorem cont.
Solution
a. Remove RL from circuit
b. Determine RTH seen from terminal a-b with all independent sources are turn off.

25. Thevenin theorem cont.
I=0 A
c. Get VTH at terminal a-b
VX − 20
=5 VTH
10
VX = 70V
VTH = V5 A = VX = 70
d. Draw the Thevenin equivalent circuit and connect the back portion
removed from the (a) above RTH=12Ω
a
VTH=70 V RL
b

26. Thevenin theorem cont.
Example 1.14
Refer to the circuit below, sketch Thevenin equivalent circuit at terminal
a-b, next calculate the current flowing, I3Ω and voltage across,V3Ω the
resistor 3Ω,
5Ω 1Ω
a
I3Ω
4Ω V3Ω 3Ω
28 V
b

27. Thevenin theorem cont.
Example 1.16
Refer to the circuit below, get the value of V1/3Ω
½Ω
3V
½Ω
2A ¼Ω 1/3 Ω V1/3Ω

28. Norton theorem
This theorem is in use to facilitate a complex
circuit network to a simple circuit called the Norton
equivalent circuit.
This equivalent circuit consists of a current
source IN connected in parallel with a resistor RN.
a
Complex
Circuit b

29. Norton theorem cont.
a a
Complex OFF
IN RN
Circuit Circuit
b b
The steps to get the Norton equivalent circuit:-
a. Remove section of the network where to find the Norton
equivalent circuit and mark clearly the two terminals as a-b
b. Determine the Norton equivalent resistance seen from the
terminal a-b with independent sources is turn off
c. Get the Norton current value of current flowing through
the terminals a-b when a short circuit in the terminal. (various
method can be used to obtain IN, whether to used loop
analysis/nod analysis)
d. Draw the Norton equivalent circuit and connect the back portion
removed from the (a) above

30. Norton theorem cont.
Examples
Determine Norton equivalent circuit at terminals a-b for circuit below.
Next calculate current flowing and voltage across resistance 3Ω
5Ω 1Ω
a
I3Ω
4Ω V3Ω 3Ω
28 V
b

31. Norton theorem cont.
Solution.
a. Remove RL from circuit
b. Determine RN seen from terminal a-b with all independent sources are turn off.
RN=(1+(5//4))=3.22 Ω

32. Norton theorem cont.
IT
c. Get IN at terminal a-b (short a-b)
IN
4 28 4
I N = IT   =   = 3.86 A
 5  (5 + (4 //1))  5 
d. Draw the Norton equivalent circuit and connect the back portion
removed from the (a) above
Current flowing 3Ω,
3.22
I 3Ω = ( 3.86 ) = 2 A
(3 + (3.22))
IN=3.86 A RN=3.22Ω 3Ω
Voltage across 3Ω
V3Ω = I 3Ω ( 3) = 6V

33. Norton theorem cont.
Example 1.19
Get the value of V1/3Ω
½Ω
3V
½Ω
2A ¼Ω 1/3 Ω V1/3Ω

34. Thevenin and Norton theorem with dependent sources
To analyze circuits with independent sources, (IN)
and (VTH) may be obtained by using the analysis as before.
However, the Thevenin and Norton resistance can not
be obtained directly from the network because of
dependent sources can not be turned off as an
independent source.
therefore, to solve the circuit dependent
sources, two ways:
1. Determine the value of VTH and IN, so
VTH
RN = RTH =
IN

35. Thevenin and Norton theorem with dependent
sources CONT.
2. Introduce an independent voltage source,VT or
an independent current source, IT at the root a-b. VT
and IT value is any value. However,
free resources available on the network must be turned
off prior circuit.
I a a
Off VT Off Vab IT
Circuit b Circuit b
VT Vab
RTH = RN = Ω RTH = RN = Ω
I IT

36. Thevenin and Norton theorem with dependent
sources CONT.
Example 1.20
Sketch the Thevenin equivalent circuit at terminal a-b, next calculate value Iab

37. Thevenin and Norton theorem with dependent
sources CONT.
Solution.
a) Remove resistance 3 Ω from circuit
-+
b) Get the value VTH
Write equation every loop

38. Thevenin and Norton theorem with
dependent sources CONT.
Solve the equation above to get value I2, next find value VTH
c) Get resistance value of Thevenin equivalent, RTH
RTH can be solve in two way.
i) Get value IN
-+

39. Thevenin and Norton theorem with
dependent sources CONT.
ii) Introduce an independent source.
1. introduce independent voltage source
-+

40. Thevenin and Norton theorem with
dependent sources CONT.
II. introduce independent current source

41. Thevenin and Norton theorem with
dependent sources CONT.
So, sketch the Thevenin equivalent circuit
VTH=48.2 V

42. Relationship between the Thevenin and Norton theorem
Thevenin equivalent circuit can be converted into the
Norton equivalent circuit or vice versa by changing the
concept (super transformation)of supply where: -
a) Thevenin resistance (RTH) value is equal to the Norton
resistance (RN)

43. Maximum power transfer
a circuit will supply maximum power to the load if
the load resistance RL is equal to the equivalent
resistance seen by the load
Maximum power transfer can be obtained by
replace a complex circuit with the Thevenin equivalent
circuit or Norton equivalent circuit

44. Maximum power transfer cont.
2
Power to the load RL,  VTH 
PRL = I RL = 
2
 RL
 RTH + RL 
Condition maximum power transfer RL = RTH
Therefore, maximum power supplied to the load is:
VTH 2 VTH 2
PRLmak = =
4 RL 4 RTH

45. Maximum power transfer cont.
2
V Th
R L = R Th p max =
4 R Th

46. Maximum power transfer cont.
Examples
From circuit below, calculate:-
a) Value RL when maximum output power
b) Maximum power absorb by load RL

47. Maximum power transfer cont.
Solution.
a) Remove RL from circuit and off all source from circuit to find RTH
b) Get the thevenin voltage at terminal a-b when RL removed from circuit

48. Maximum power transfer cont.
So, draw Thevenin equivalent circuit when maximum power transfer happen.

49. Maximum power transfer cont.
Examples 1.22
From circuit below, calculate:-
a) Value RL when maximum output power
b) Maximum power absorb by load RL