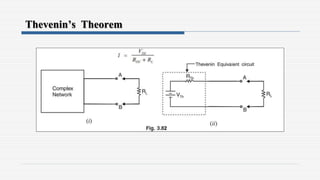
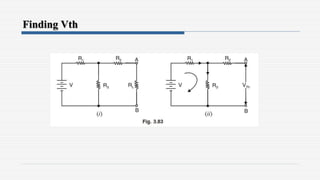
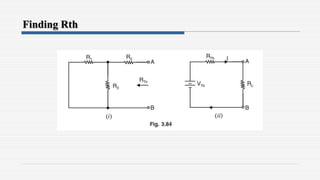
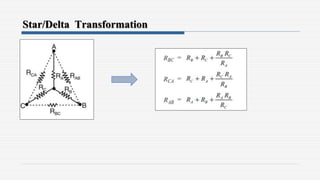
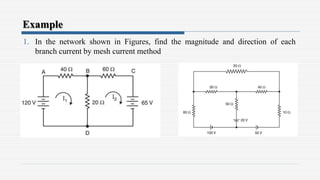
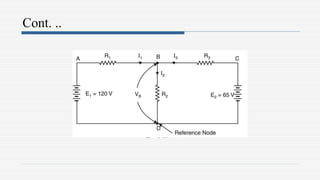
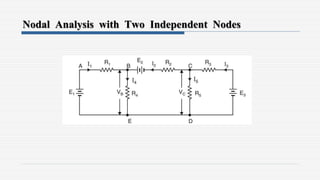
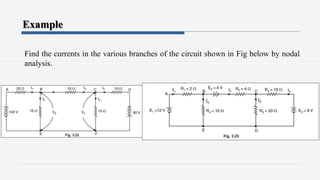
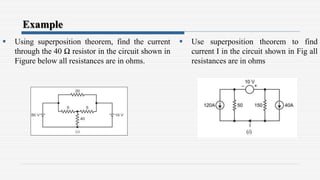
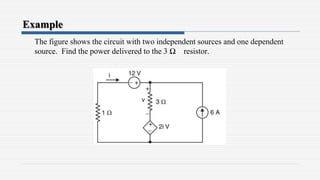
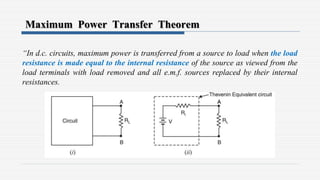
1. The document discusses various network theorems and techniques used to analyze electrical circuits, including Maxwell's mesh current method, nodal analysis, superposition theorem, Thevenin's theorem, and the maximum power transfer theorem. 2. Key terms are defined, such as linear/non-linear circuits, active/passive elements, nodes, junctions, branches, loops, and meshes. 3. Examples are provided to demonstrate applying the theorems to solve for unknown currents and voltages in circuits. The maximum power transfer theorem states that maximum power is transferred when the load resistance equals the internal resistance of the source.

1. D.C. NETWORK THEOREM
Lecture 2

2. Introduction
- Any arrangement of electrical energy sources, resistances and other circuit
elements is called an electrical network
- So far, we employed two network laws viz Ohm’s law and Kirchhoff’s laws
to solve network problems
- Occasions arise when these laws applied to certain networks do not yield
quick and easy solution.
- To overcome this difficulty, some network theorems have been developed
which are very useful in analyzing both simple and complex electrical circuits

3. Network Terminology
1. Linear circuit: A linear circuit is one whose parameters (e.g. resistances) are
constant i.e. they do not change with current or voltage.
2. Non-linear circuit: A non-linear circuit is one whose parameters (e.g.
resistances) change with voltage or current.
3. Bilateral circuit: A bilateral circuit is one whose properties are the same in
either direction. For example, transmission line is a bilateral circuit because
it can be made to perform its function equally well in either direction.

4. Cont. ..
4. Active element: An active element is one which supplies
electrical energy to the circuit
5. Passive element: A passive element is one which receives
electrical energy and then either converts it into heat
(resistance) or stores in an electric field (capacitance) or
magnetic field (inductance)
6. Node: A node of a network is an equipotential surface at which two or more circuit
elements are joined. Thus in Fig., circuit elements R1 and E1 are joined at A and
hence A is the node. Similarly, B, C and D are nodes.
7. Junction: A junction is that point in a network where three or more circuit elements
are joined. In Fig. 3.1, there are only two junction points viz. B and D. That B is a
junction is clear from the fact that three circuit elements R1, R2 and R3 are joined at it.
Similarly, point D is a junction because it joins three circuit elements R2, E1 and E2.

5. Cont. ..
8. Branch: A branch is that part of a network which lies between two junction
points. Thus referring to Fig. , there are a total of three branches viz. BAD,
BCD and BD. The branch BAD consists of R1 and E1 ; the branch BCD
consists of R3 and E2 and branch BD merely consists of R2
9. Loop: A loop is any closed path of a network. Thus in Fig., ABDA, BCDB
and ABCDA are the loops
10. Mesh: A mesh is the most elementary form of a loop and cannot be further
divided into other loops. In Fig. , both loops ABDA and BCDB qualify as
meshes because they cannot be further divided into other loops. However, the
loop ABCDA cannot be called a mesh because it encloses two loops ABDA
and BCDB

6. Cont. ..
11. Network and circuit: Strictly speaking, the term network is used for a circuit
containing passive elements only while the term circuit implies the presence
of both active and passive elements. However, there is no hard and fast rule
for making these distinctions and the terms “network” and “circuit” are often
used interchangeably.
12. Parameters: The various elements of an electric circuit like resistance (R),
inductance (L) and capacitance (C) are called parameters of the circuit. These
parameters may be lumped or distributed.
13. Unilateral circuit: A unilateral circuit is one whose properties change with
the direction of its operation. For example, a diode rectifier circuit is a
unilateral circuit. It is because a diode rectifier cannot perform rectification in
both directions.

7. Network Theorems and Techniques
1. Maxwell’s mesh current method
2. Nodal analysis
3. Superposition theorem
4. Thevenin’s theorem
5. Maximum power transfer theorem
6. Delta/star or star/delta transformation

8. Maxwell’s Mesh Current Method
- In this method, Kirchhoff’s voltage law is applied to a network to write mesh
equations in terms of mesh currents instead of branch currents
- Each mesh is assigned a separate mesh current. This mesh current is assumed
to flow clockwise around the perimeter of the mesh without splitting at a
junction into branch currents. Kirchhoff’s voltage law is then applied to write
equations in terms of unknown mesh currents.
- If the value of any mesh current comes out to be negative in the solution, it
means that true direction of that mesh current is anticlockwise i.e. opposite to
the assumed clockwise direction.

9. Kirchhoff’s voltage law is applied to write equation for each mesh in terms of mesh
currents. Remember, while writing mesh equations, rise in potential is assigned
positive sign and fall in potential negative sign.

11. Example
1. In the network shown in Figures, find the magnitude and direction of each
branch current by mesh current method

12. Nodal Analysis
- The branch currents in the circuit can be found by Kirchhoff’s laws or
Maxwell’s mesh current method. In this method, one of the nodes (Remember
a node is a point in a network where two or more circuit elements meet) is
taken as the reference node. The potentials of all the points in the circuit are
measured w.r.t. this reference node. The fixed-voltage nodes are called
dependent nodes
- Hence nodal analysis essentially aims at choosing a reference node in the
network and then finding the unknown voltages at the independent nodes
w.r.t. reference node. For a circuit containing N nodes, there will be N–1
node voltages, some of which may be known if voltage sources are present.

13. Cont. ..

14. Nodal Analysis with Two Independent Nodes

15. Example
Find the currents in the various branches of the circuit shown in Fig below by nodal
analysis.

16. Superposition Theorem
- Superposition is a general principle that allows us to determine the effect of
several energy sources (voltage and current sources) acting simultaneously in
a circuit by considering the effect of each source acting alone, and then
combining (superposing) these effects
This theorem as applied to d.c. circuits may be stated as
- In a linear, bilateral d.c. network containing more than one energy source,
the resultant potential difference across or current through any element is
equal to the algebraic sum of potential differences or currents for that element
produced by each source acting alone with all other independent ideal
voltage sources replaced by short circuits and all other independent ideal
current sources replaced by open circuits (non-ideal sources are replaced by
their internal resistances).

17. Cont. ..
Procedure. The procedure for using this theorem to solve d.c. networks is
as under :
i. Select one source in the circuit and replace all other ideal voltage sources by
short circuits and ideal current sources by open circuits.
ii. Determine the voltage across or current through the desired element/branch
due to single source selected in step (i).
iii. Repeat the above two steps for each of the remaining sources.
iv. Algebraically add all the voltages across or currents through the
element/branch under consideration. The sum is the actual voltage across or
current through that element/branch when all the sources are acting
simultaneously.

18. Example
 Using superposition theorem, find the current
through the 40 Ω resistor in the circuit shown in
Figure below all resistances are in ohms.
 Use superposition theorem to find
current I in the circuit shown in Fig all
resistances are in ohms

19. Example
The figure shows the circuit with two independent sources and one dependent
source. Find the power delivered to the 3 Ω resistor.

20. Thevenin’s Theorem

21. Finding Vth

22. Finding Rth

23. Procedure for Finding Thevenin Equivalent Circuit
i. Open the two terminals (i.e., remove any load) between which you want to find
Thevenin equivalent circuit.
ii. Find the open-circuit voltage between the two open terminals. It is called Thevenin
voltage VTh.
iii. Determine the resistance between the two open terminals with all ideal voltage
sources shorted and all ideal current sources opened (a non-ideal source is replaced
by its internal resistance). It is called Thevenin resistance RTh.
iv. Connect VTh and RTh in series to produce Thevenin equivalent circuit between the
two terminals under consideration.
v. Place the load resistor removed in step (i) across the terminals of the Thevenin
equivalent circuit. The load current can now be calculated using only Ohm’s law and
it has the same value as the load current in the original circuit.

24. Example
Calculate the current in the 50 Ω resistor in the network shown in Fig

25. Advantages of Thevenin’s Theorem
i. It reduces a complex circuit to a simple circuit viz. a single source of e.m.f. 𝑉𝑇ℎ
in series with a single resistance 𝑅𝑇ℎ.
ii. It greatly simplifies the portion of the circuit of lesser interest and enables us to
view the action of the output part directly.
iii. This theorem is particularly useful to find current in a particular branch of a
network as the resistance of that branch is varied while all other resistances and
sources remain constant.
iv. Thevenin’s theorem can be applied in successive steps. Any two points in a
circuit can be chosen and all the components to one side of these points can be
reduced to Thevenin’s equivalent circuit.

26. Maximum Power Transfer Theorem
“In d.c. circuits, maximum power is transferred from a source to load when the load
resistance is made equal to the internal resistance of the source as viewed from the
load terminals with load removed and all e.m.f. sources replaced by their internal
resistances.

27. Proof of Maximum Power Transfer Theorem
- Consider a voltage source 𝑉 of internal resistance 𝑅𝑖 delivering power to a
load 𝑅𝐿. We shall prove that when 𝑅𝐿 = 𝑅𝑖, the power delivered to RL is
maximum
- For a given source, generated voltage V and internal resistance Ri are
constant.
- Therefore, power delivered to the load depends upon 𝑅𝐿. In order to find the
value of 𝑅𝐿 for which the value of P is maximum, differentiate eq. w.r.t. 𝑅𝐿
and set the result equal to zero.

29. Important Points
The following points are worth noting about maximum power transfer
1. The circuit efficiency at maximum power transfer is only 50% as one-half of
the total power generated is dissipated in the internal resistance Ri of the
source.
2. Under the conditions of maximum power transfer, the load voltage is one-half
of the open- circuited voltage at the load terminals.

31. Example
1. Two identical cells connected in series deliver a maximum power of 1W to a
resistance of 4 Ω. What is the internal resistance and e.m.f. of each cell ?
2. What percentage of maximum possible power is delivered to RL in Fig when
RL = 2 RTh ?

32. Delta/Star and Star/Delta Transformation
- There are some networks in which the resistances are neither in series nor in
parallel.
- A familiar case is a three terminal network e.g. delta network or star network.

33. Delta/Star Transformation
Thus to find the star resistance that connects to terminal A, divide the product of the two delta
resistors connected to A by the sum of the delta resistors. Same is true for terminals B and C.

34. Star/Delta Transformation