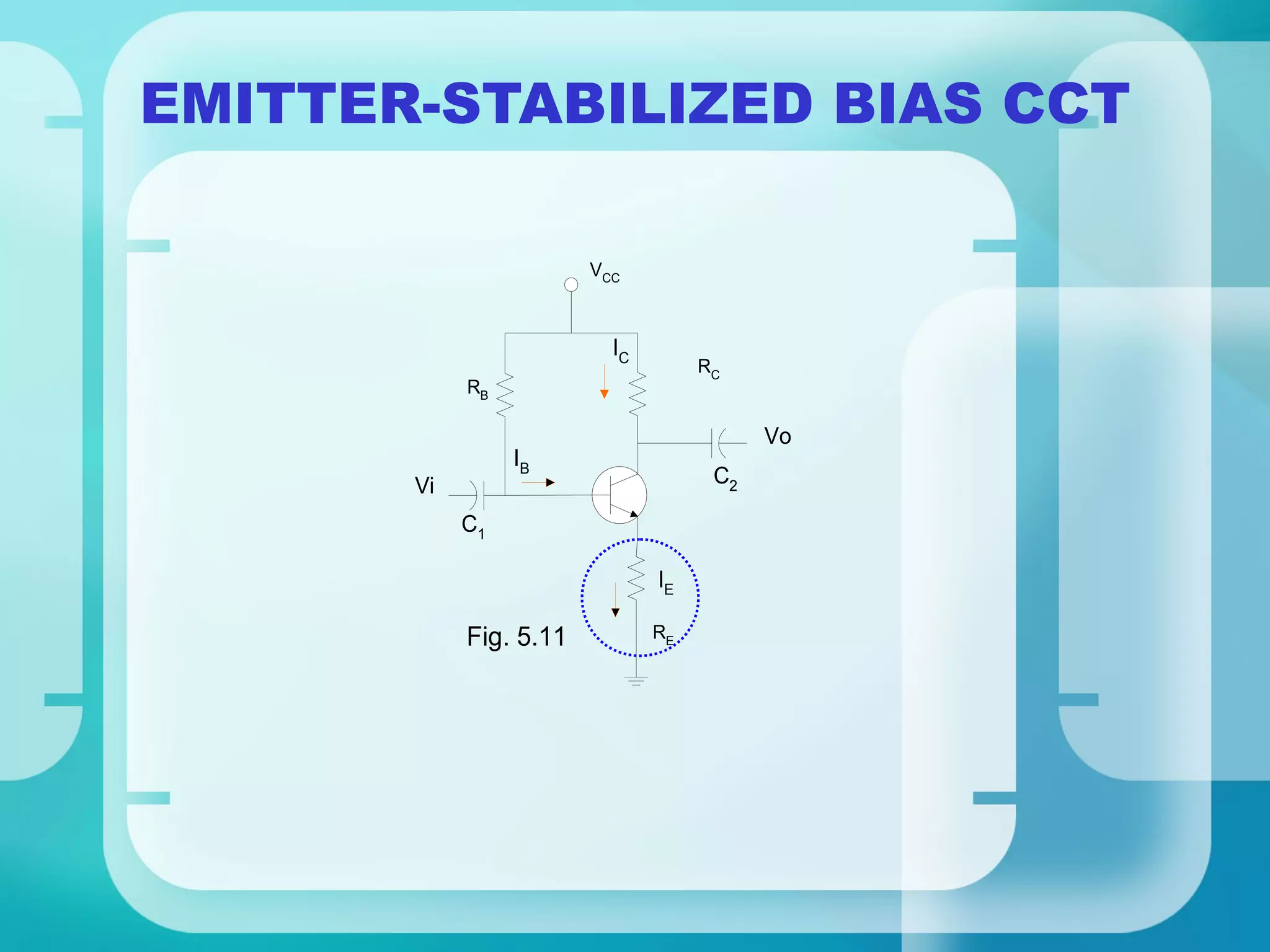
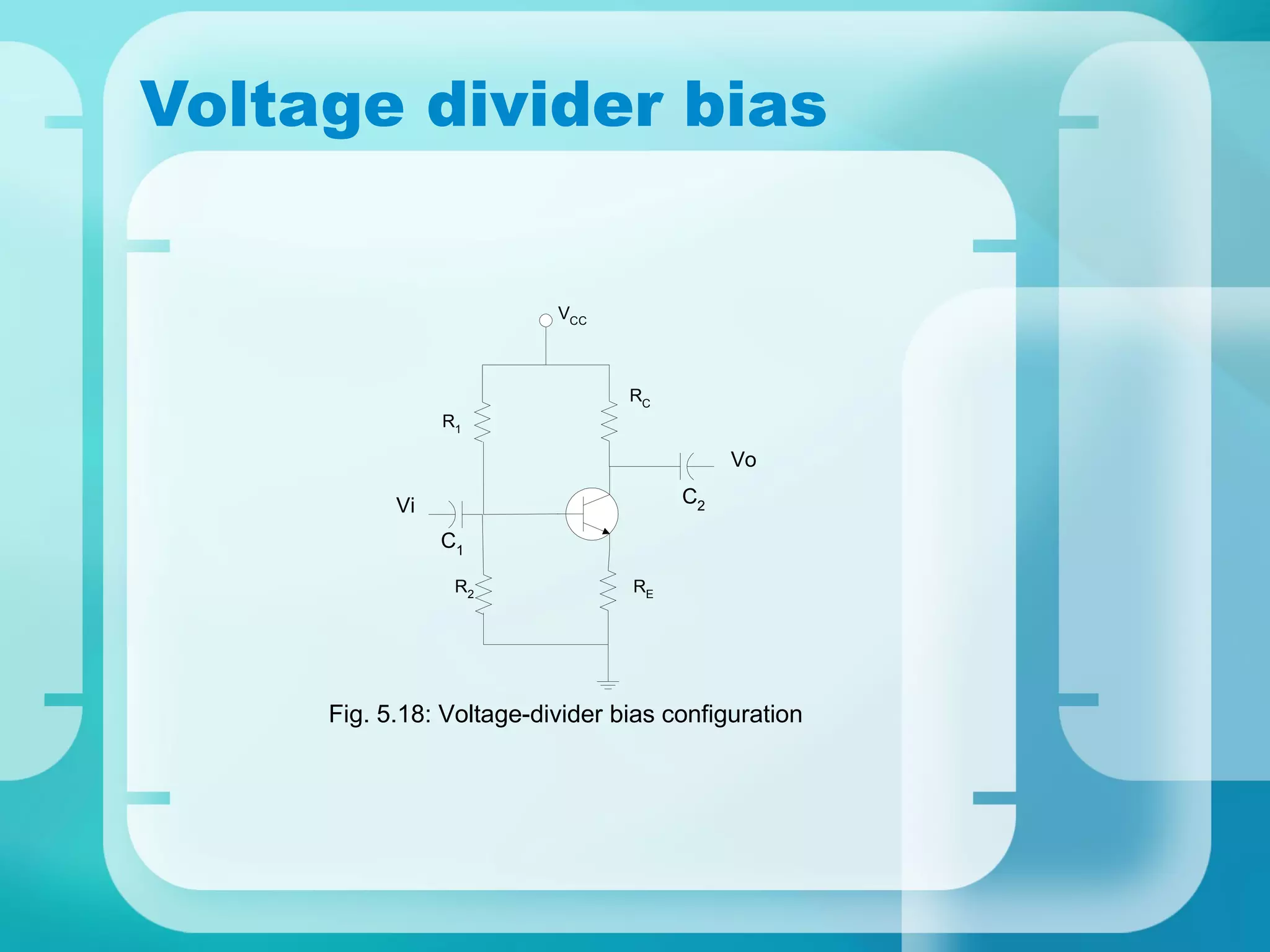
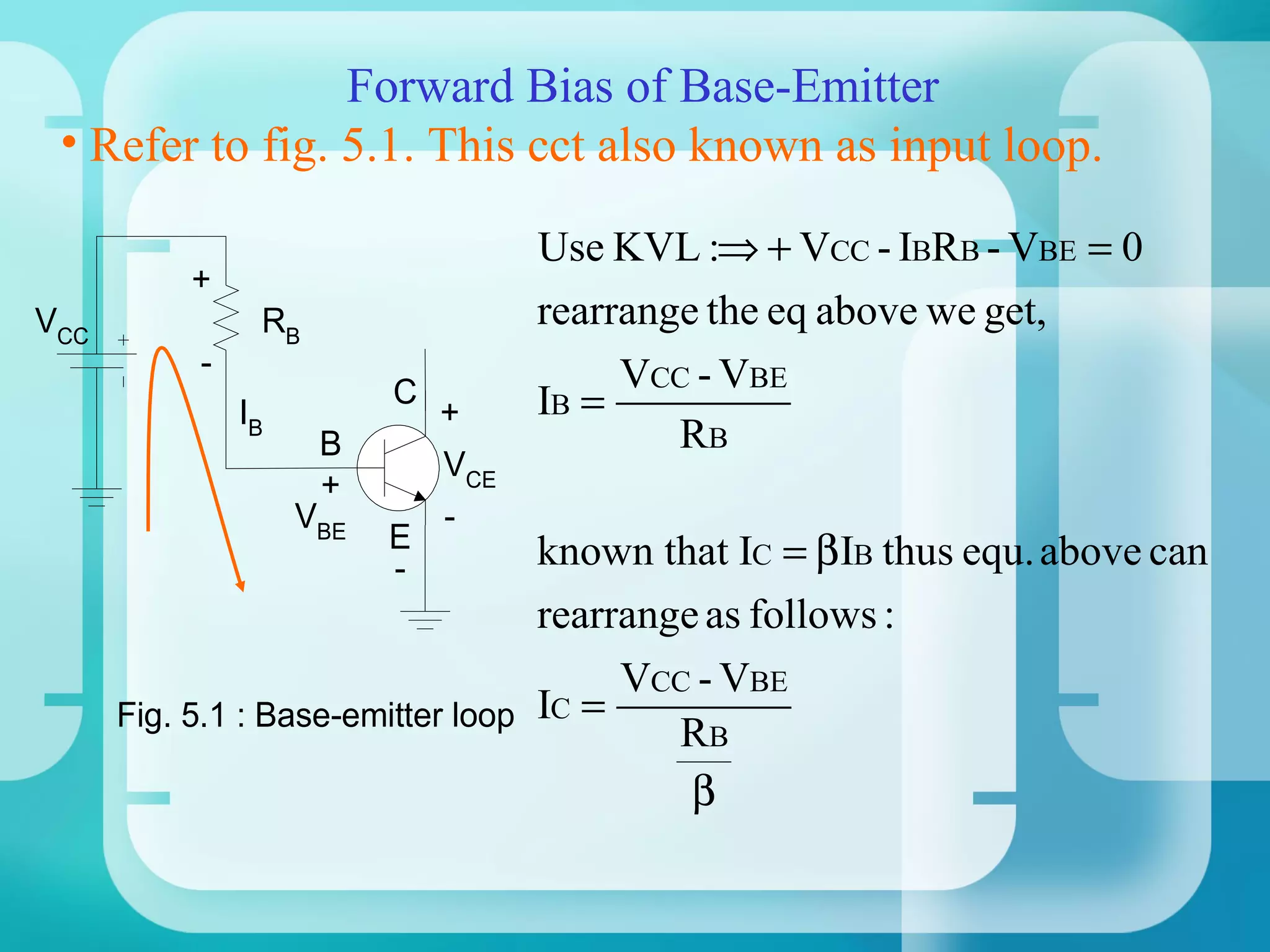
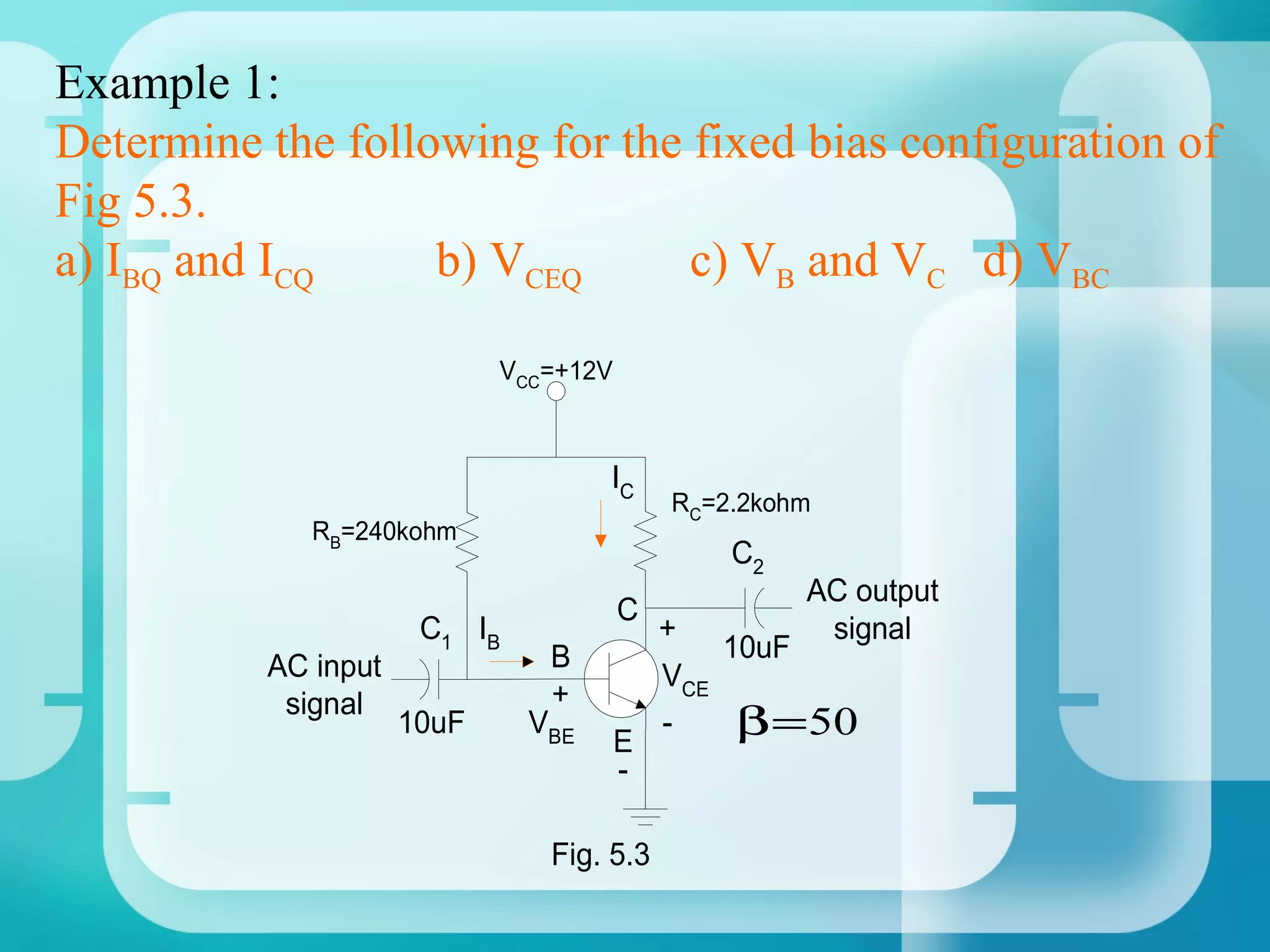
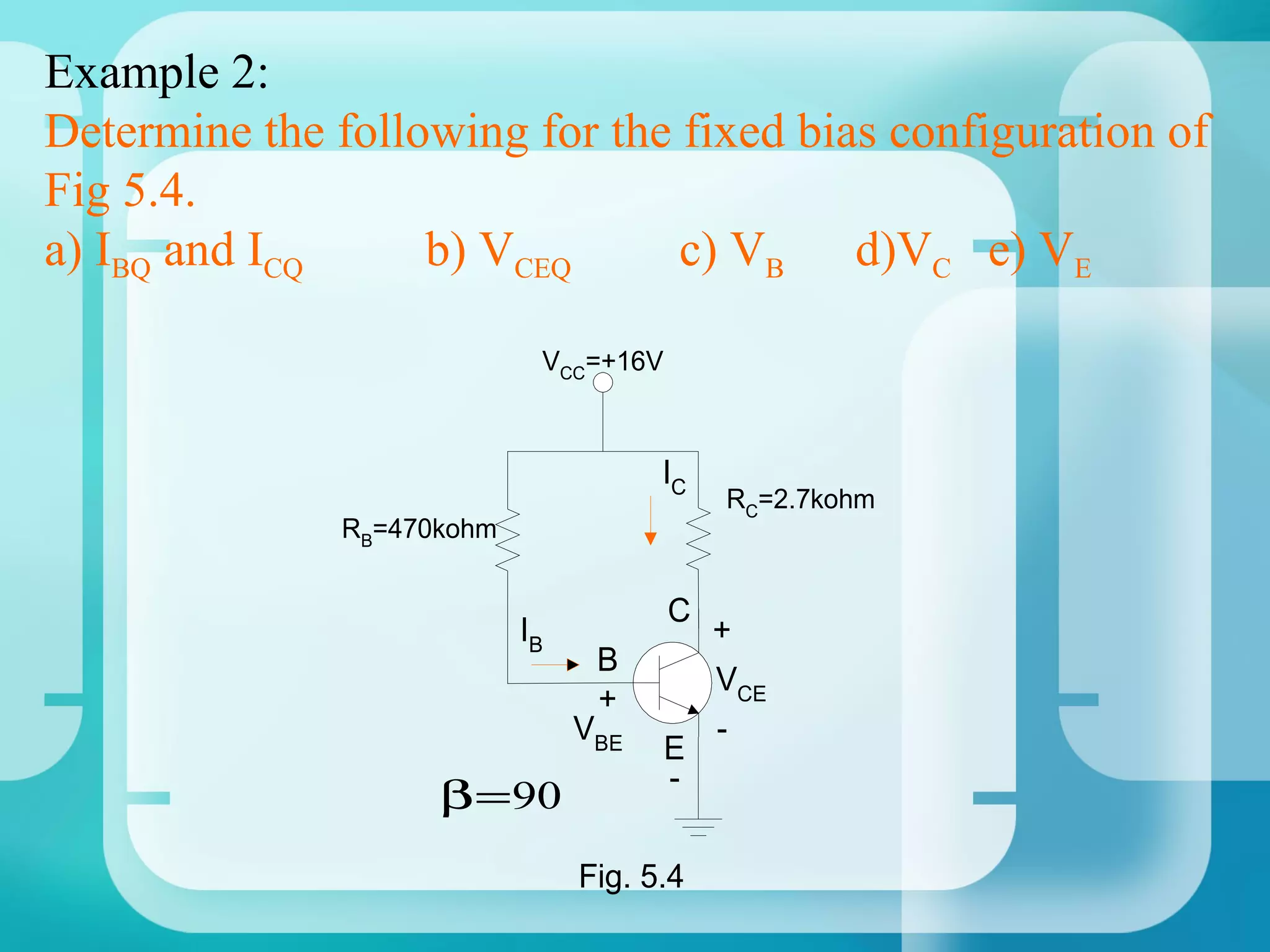
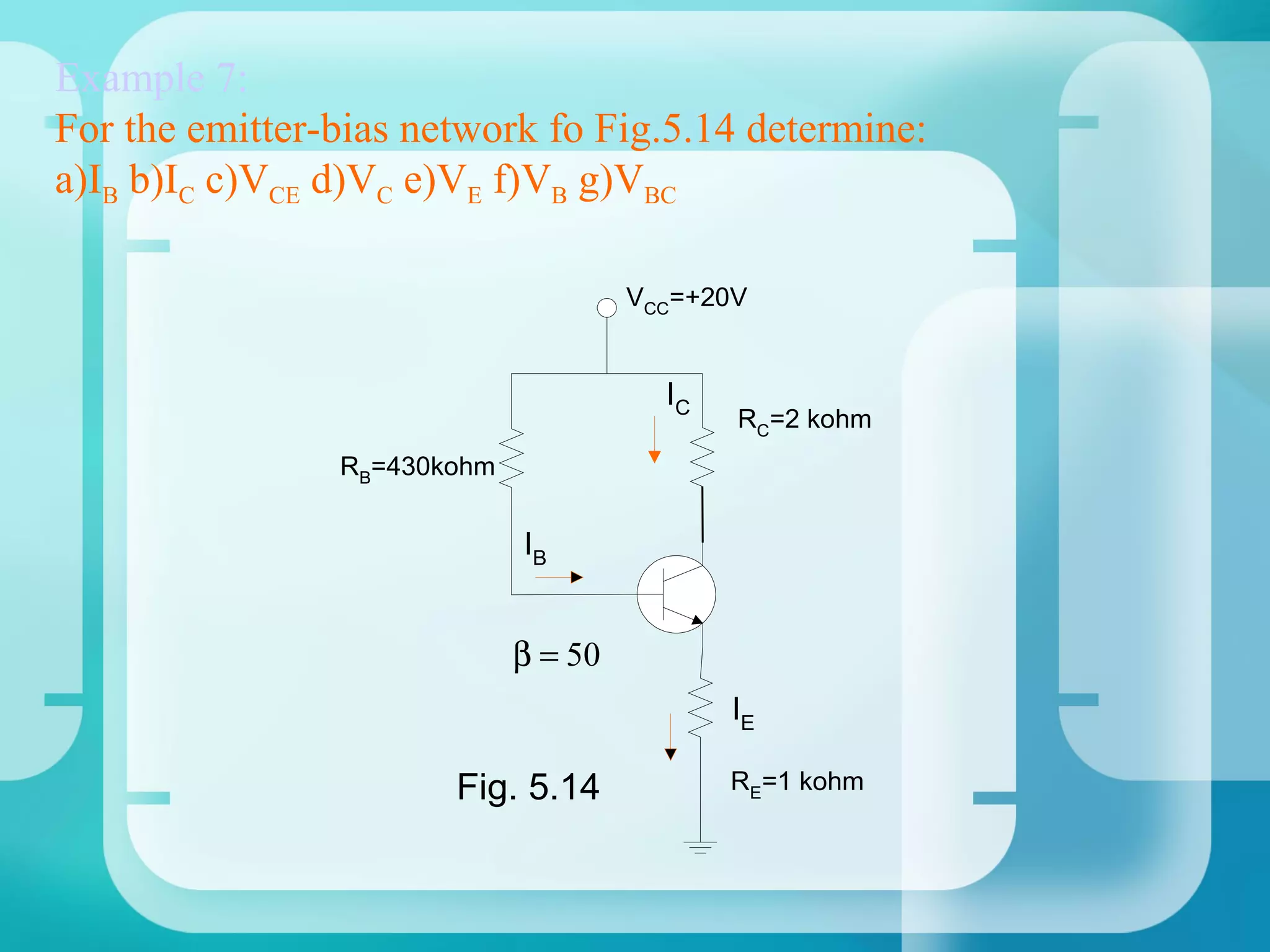
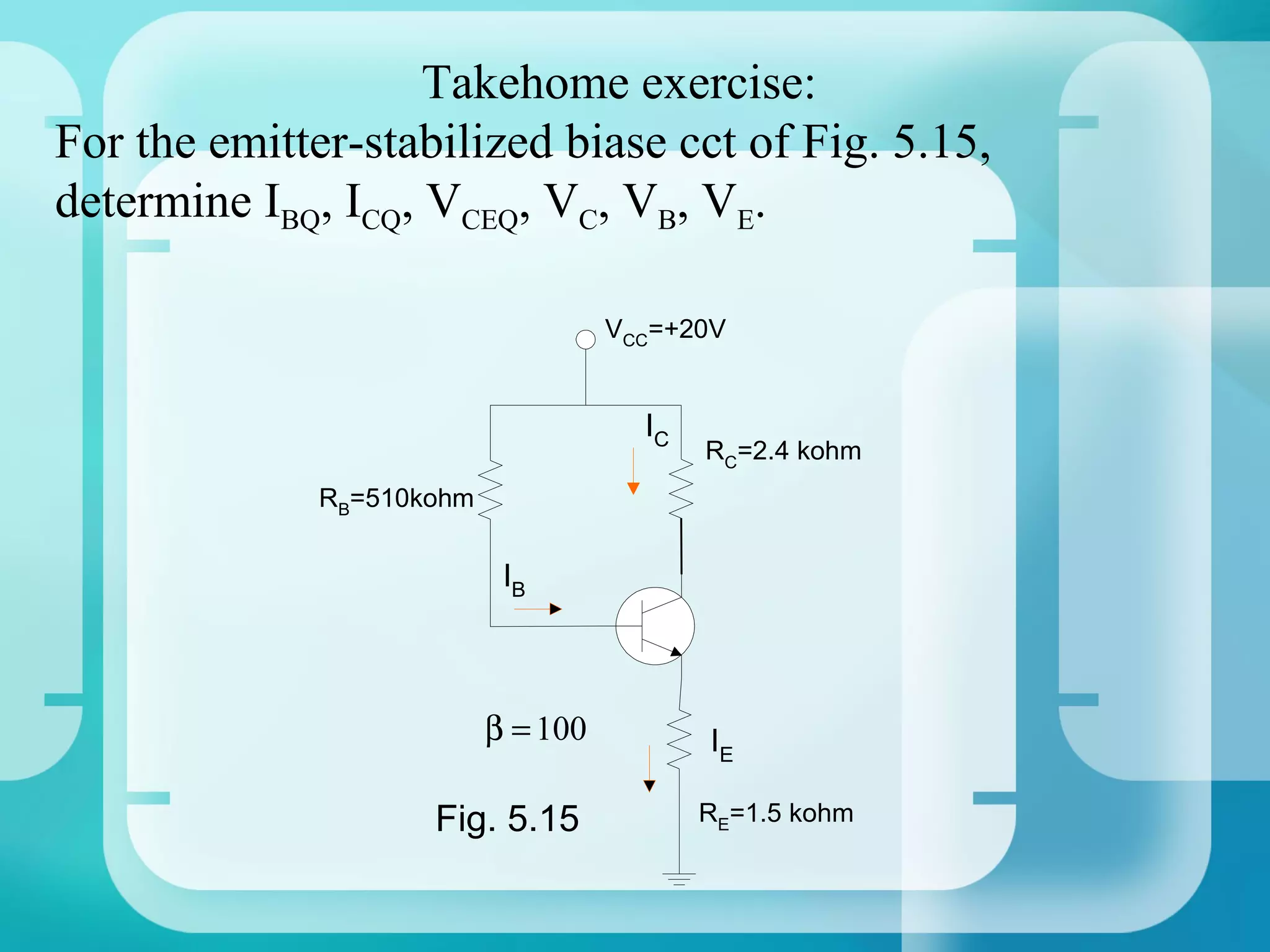
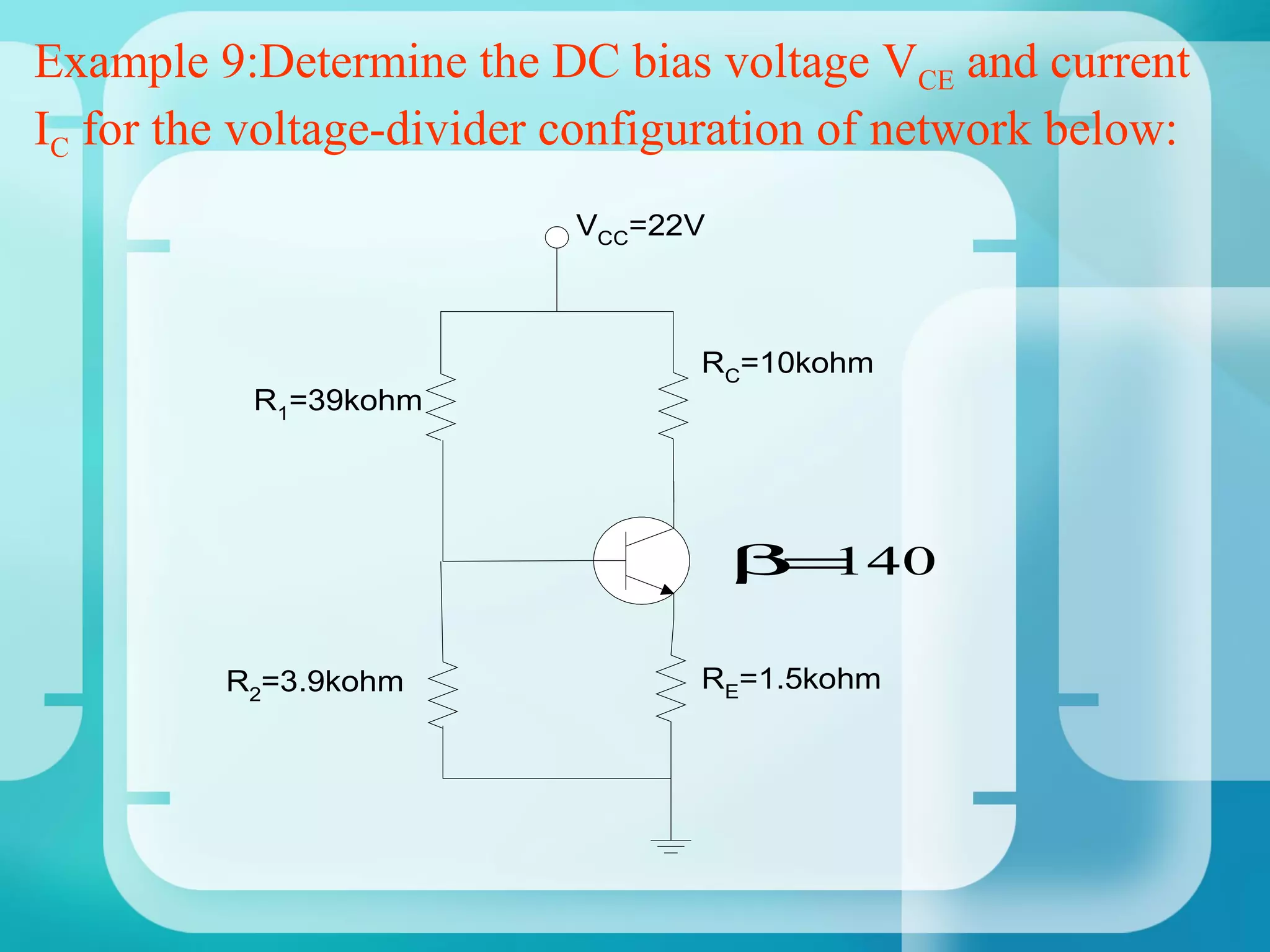
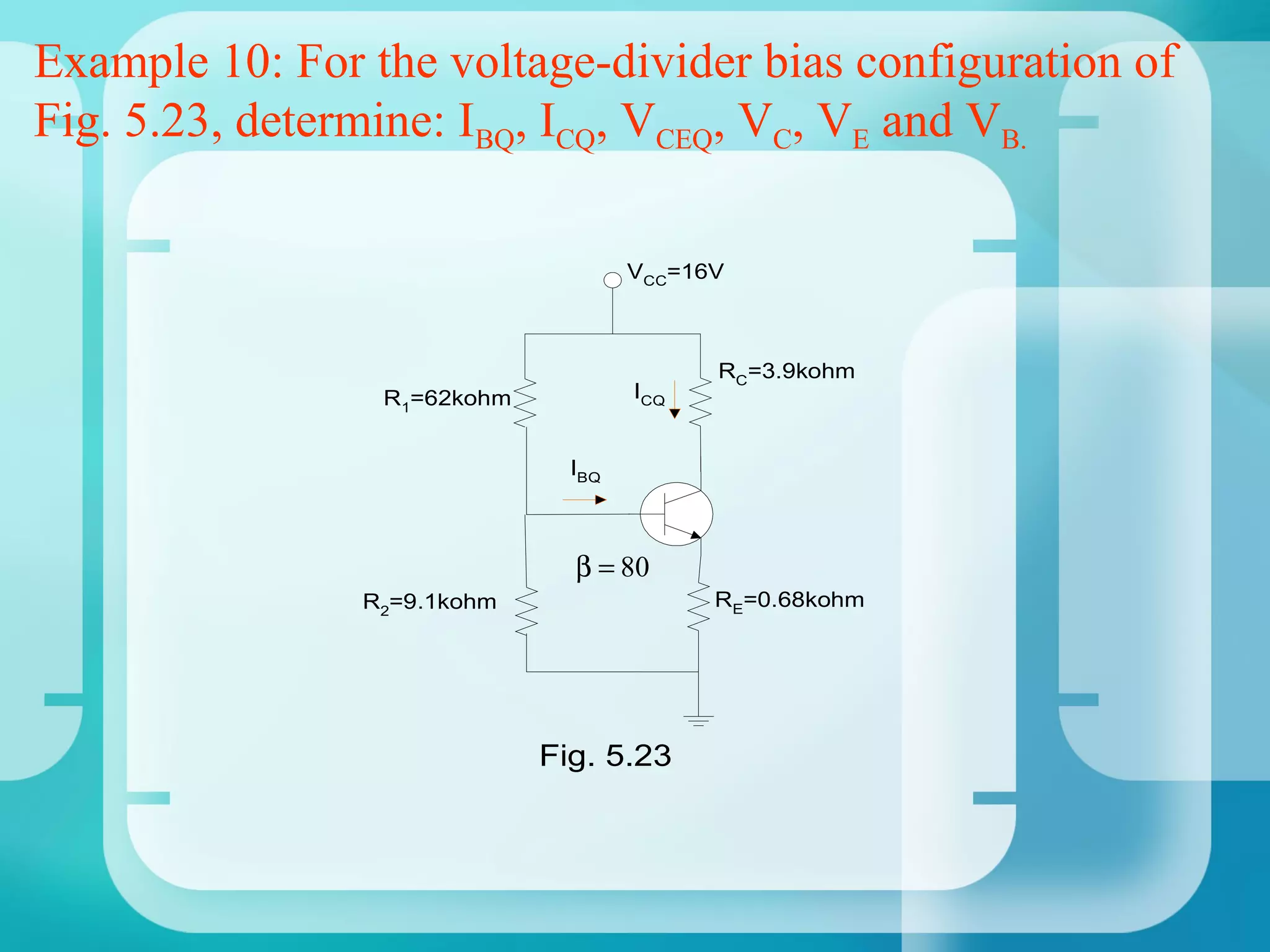
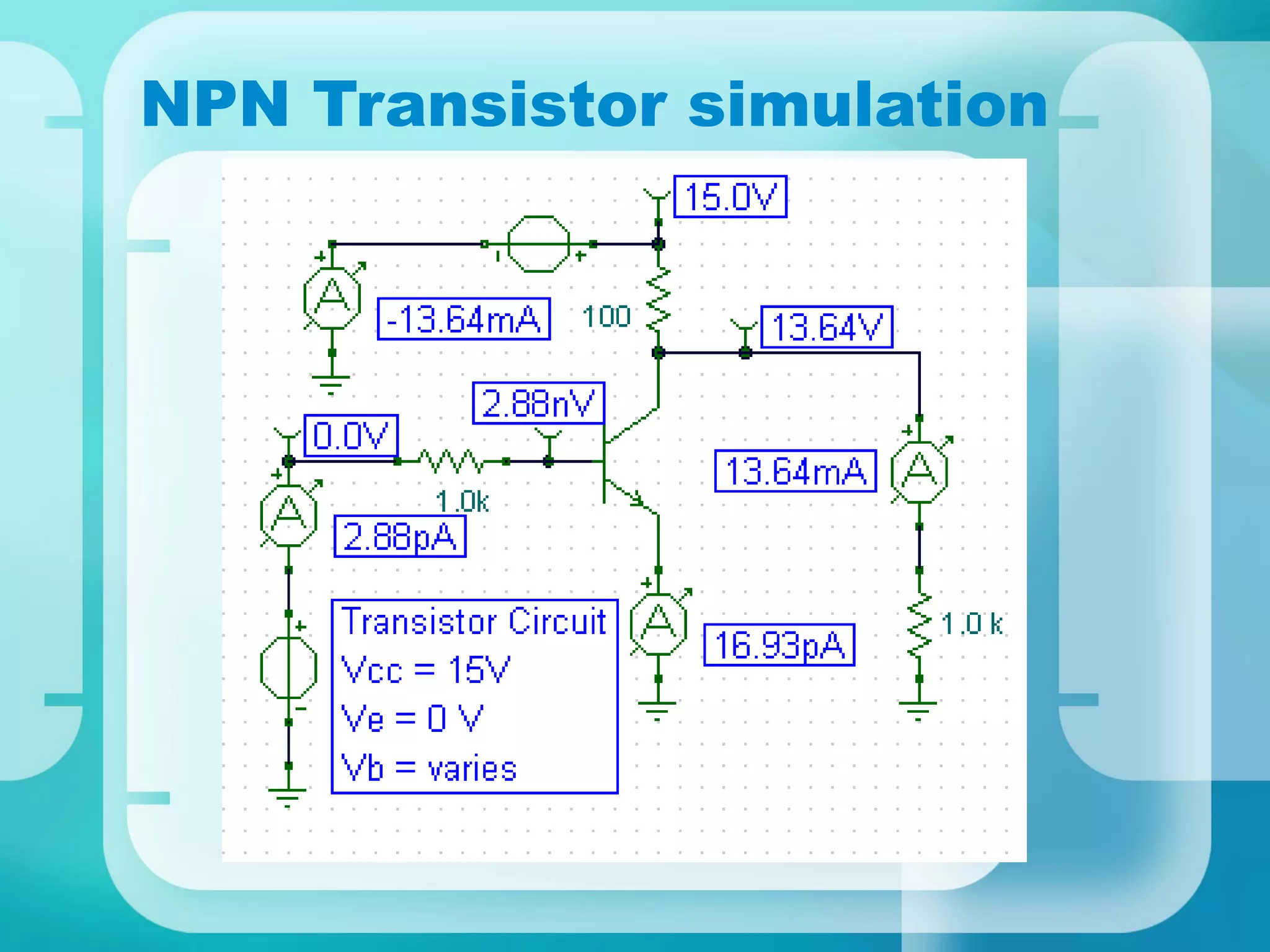
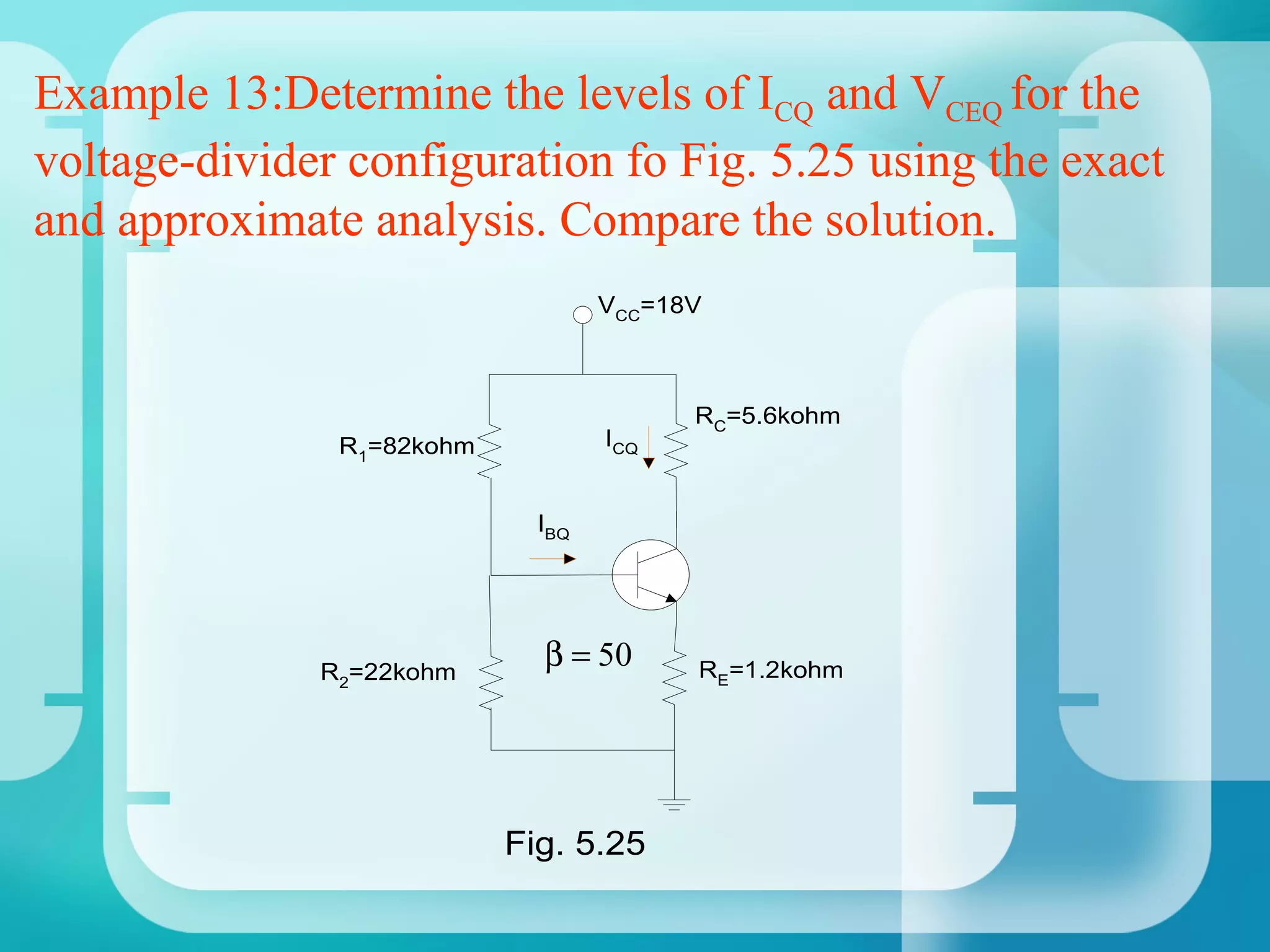
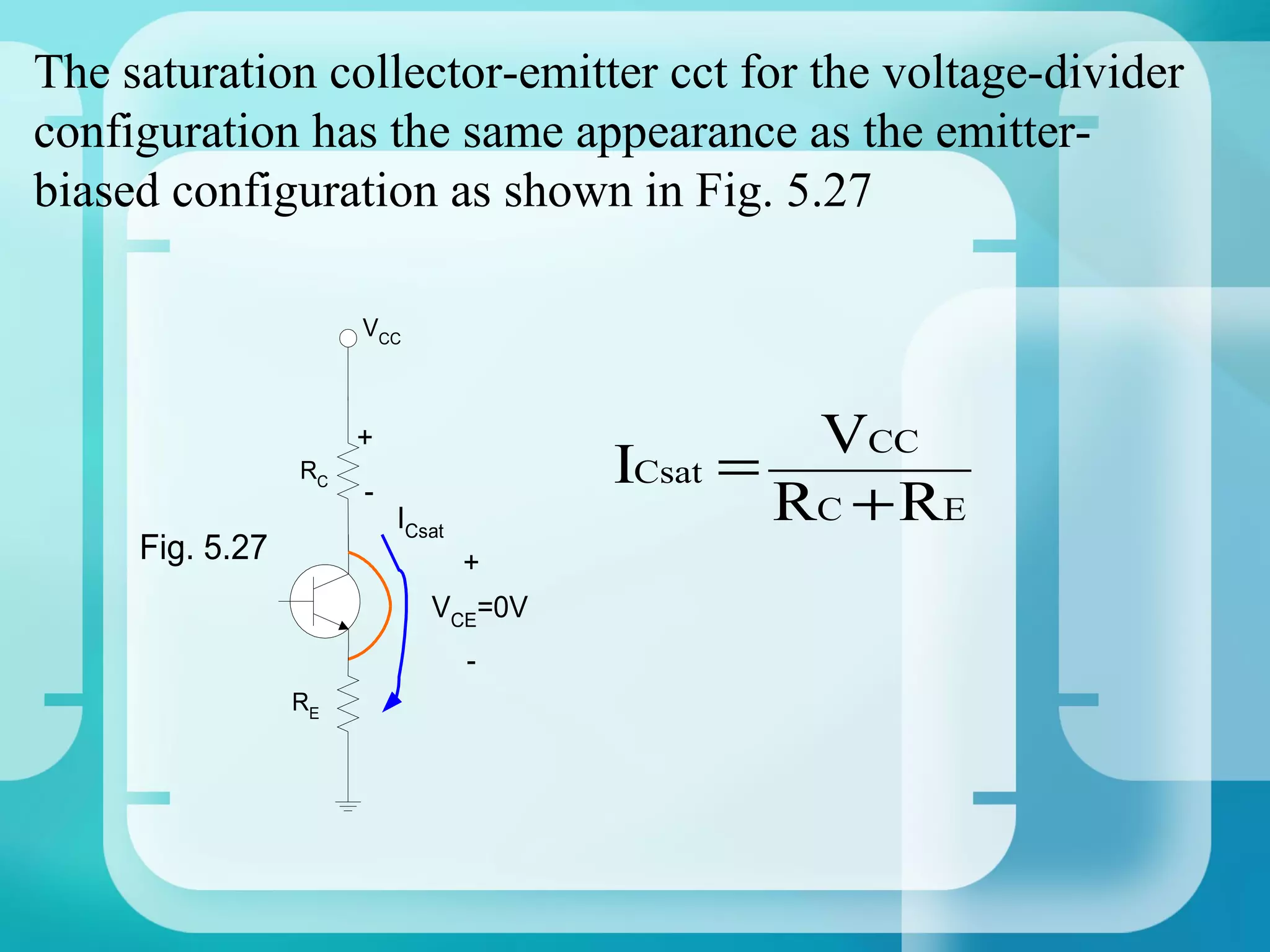
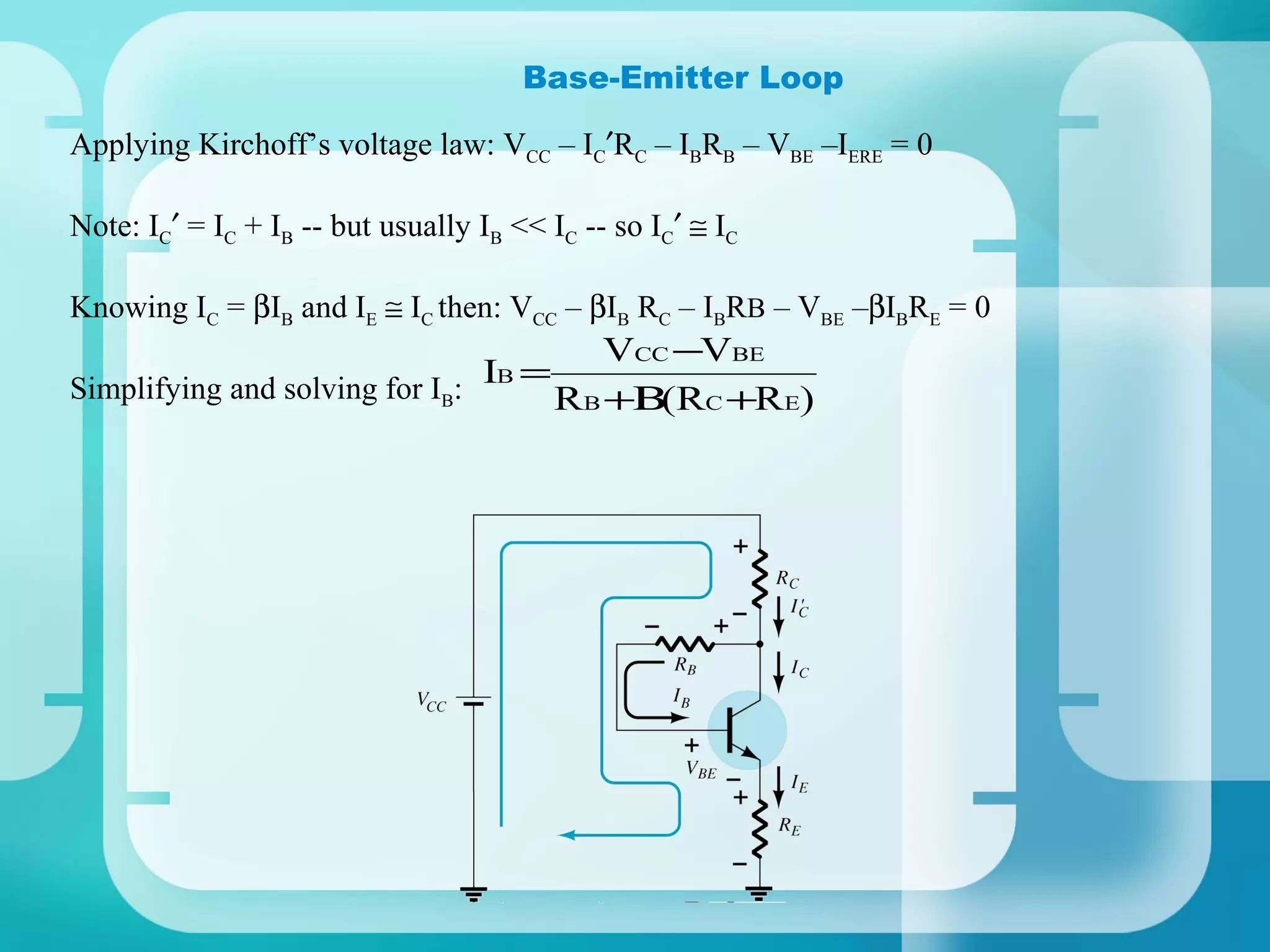
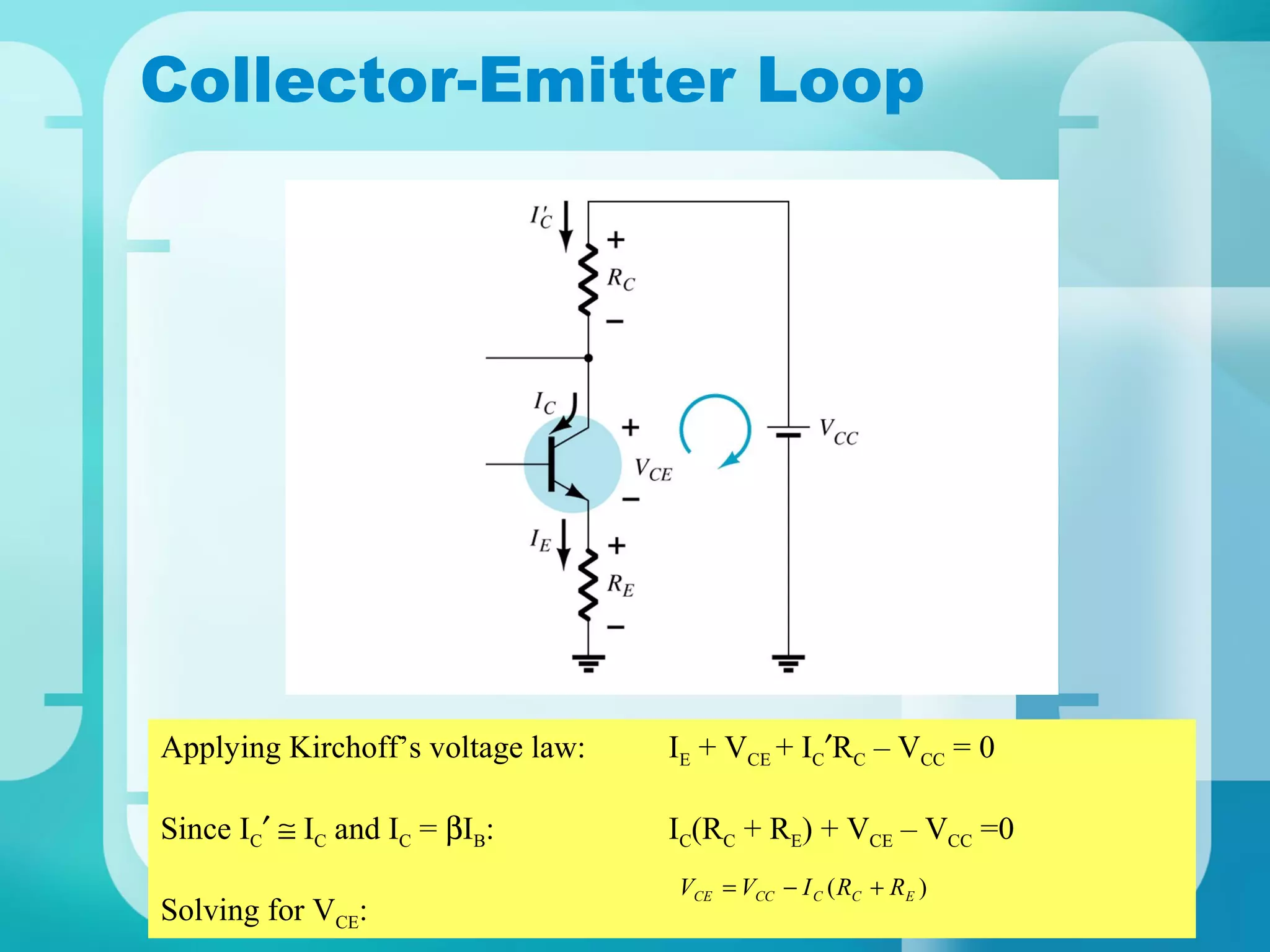
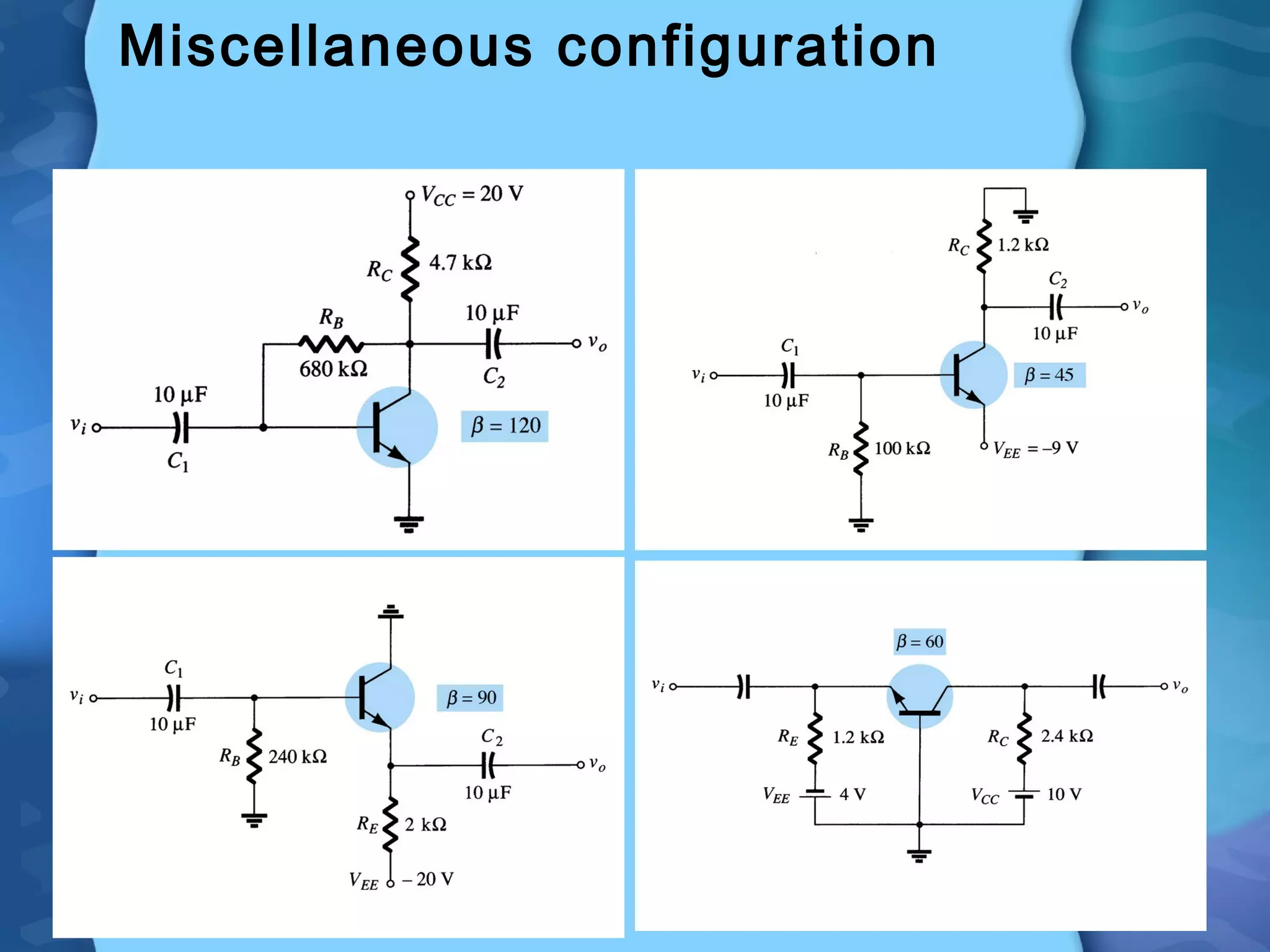
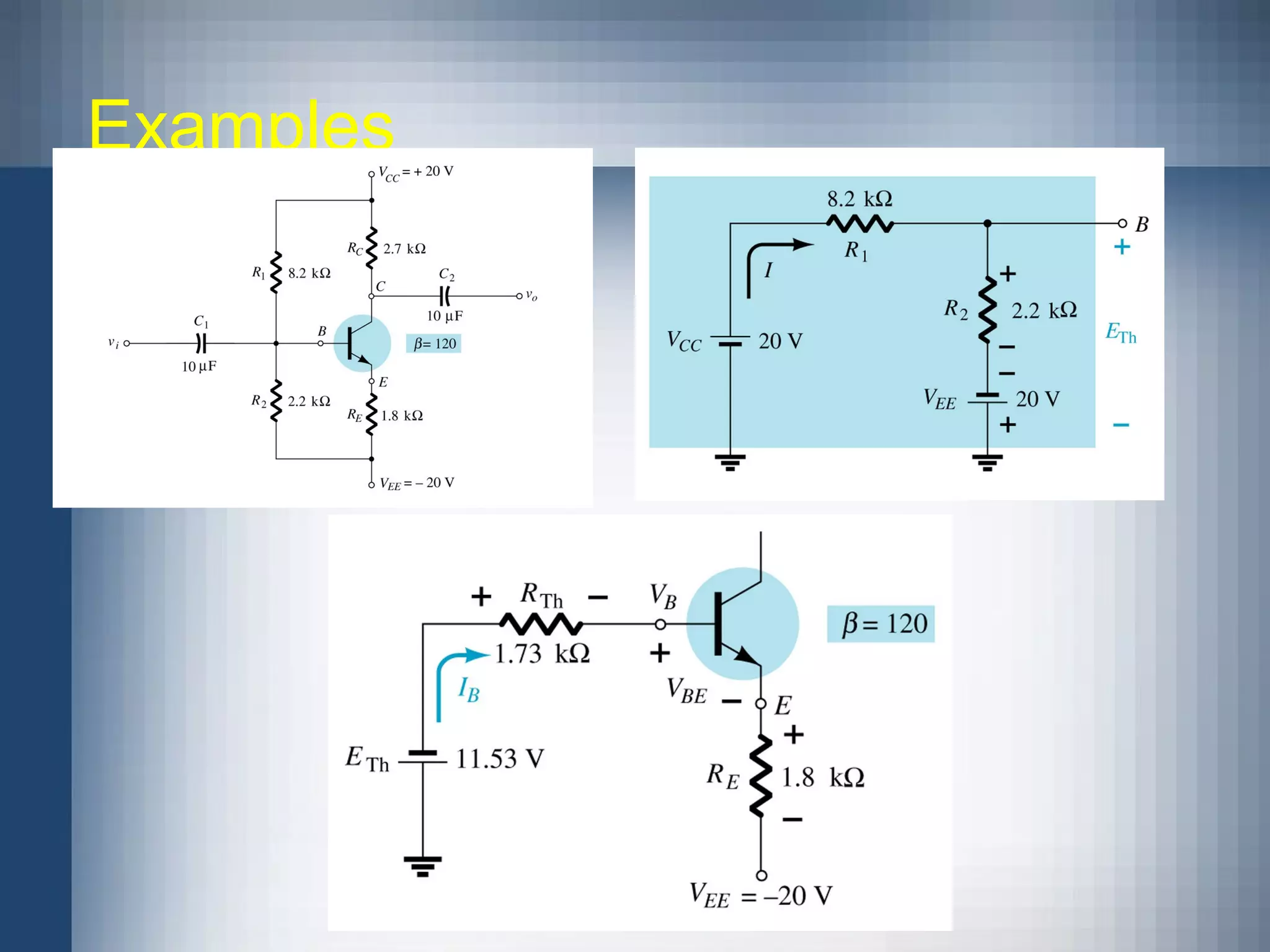
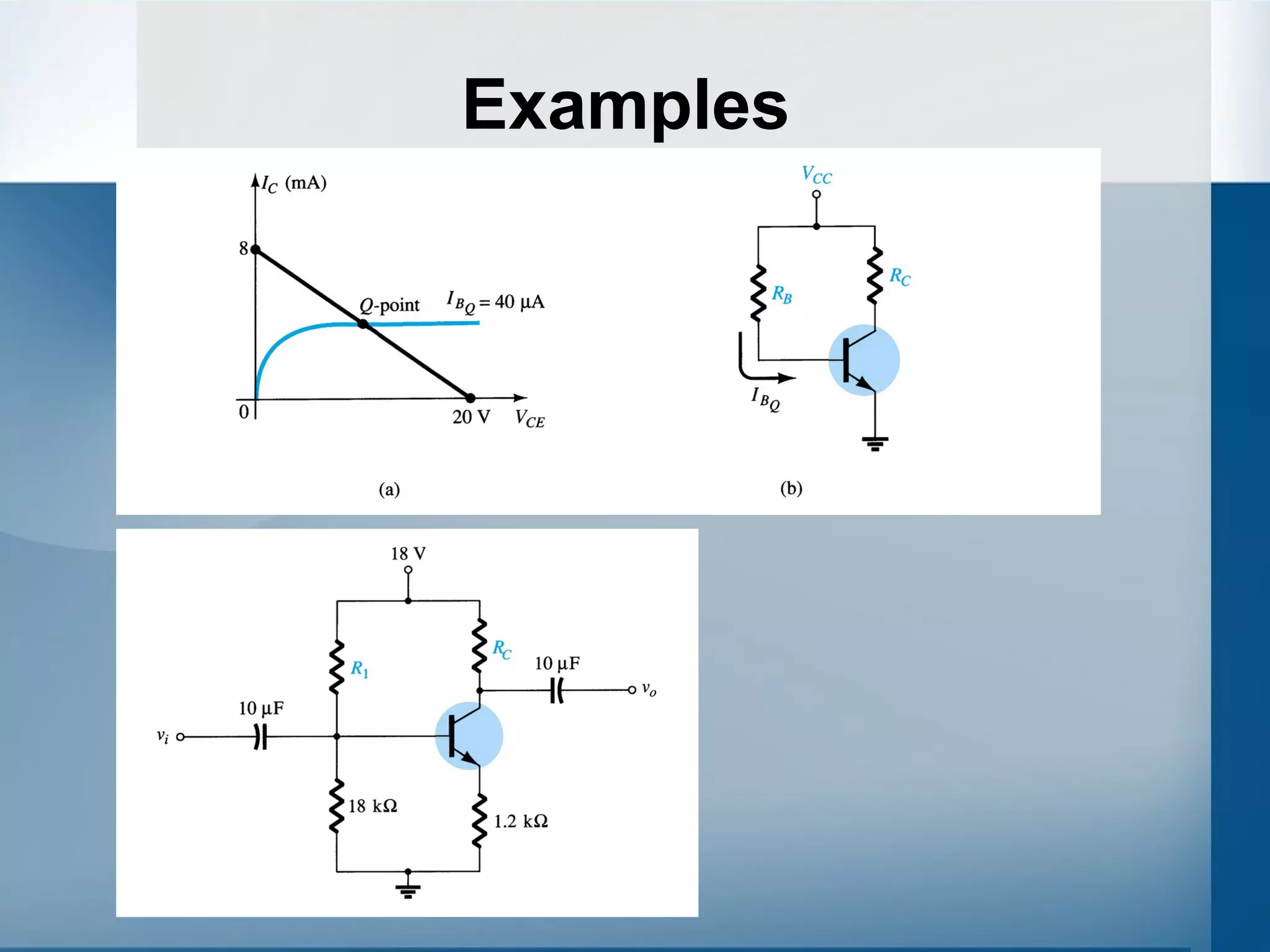
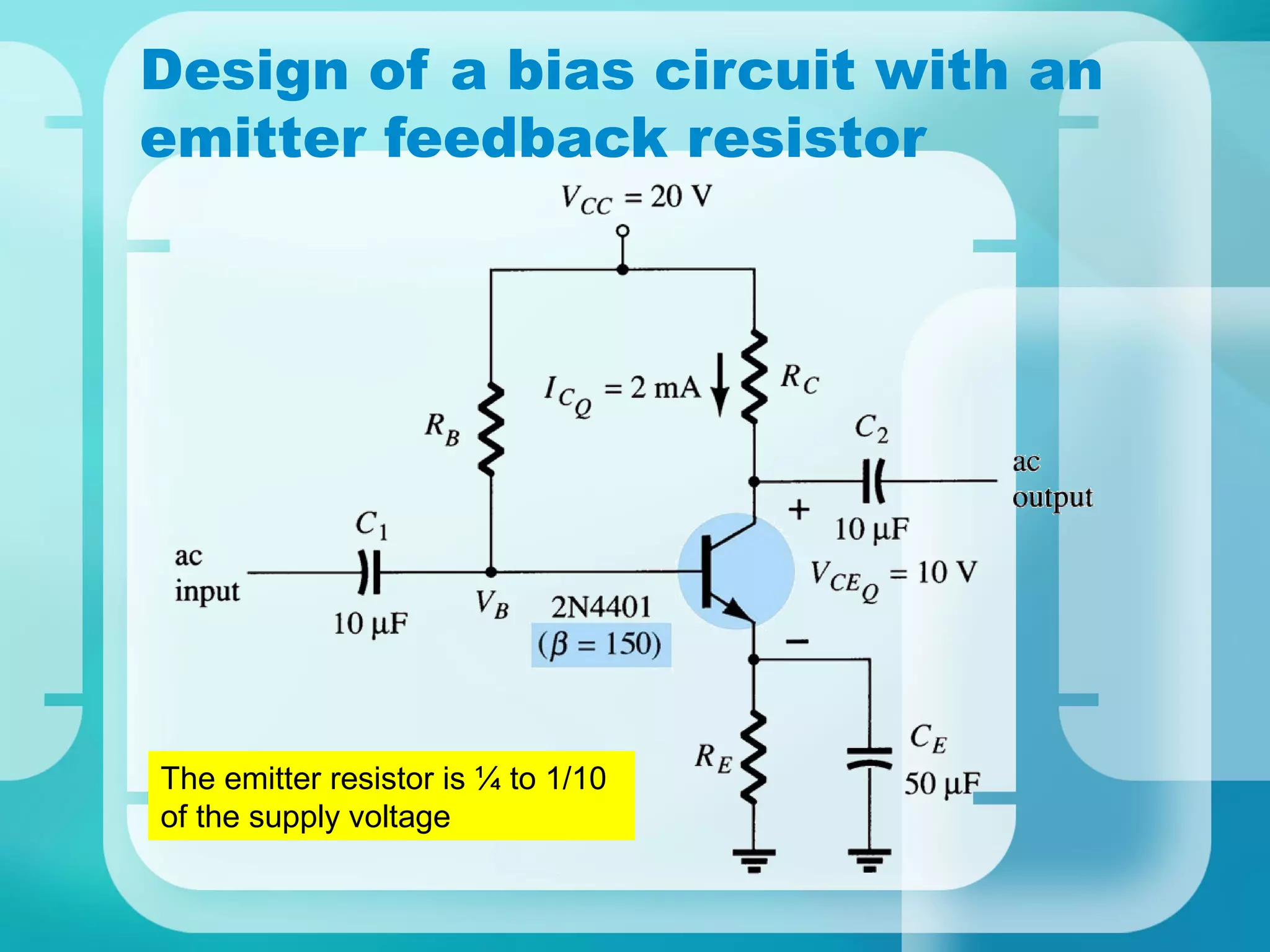
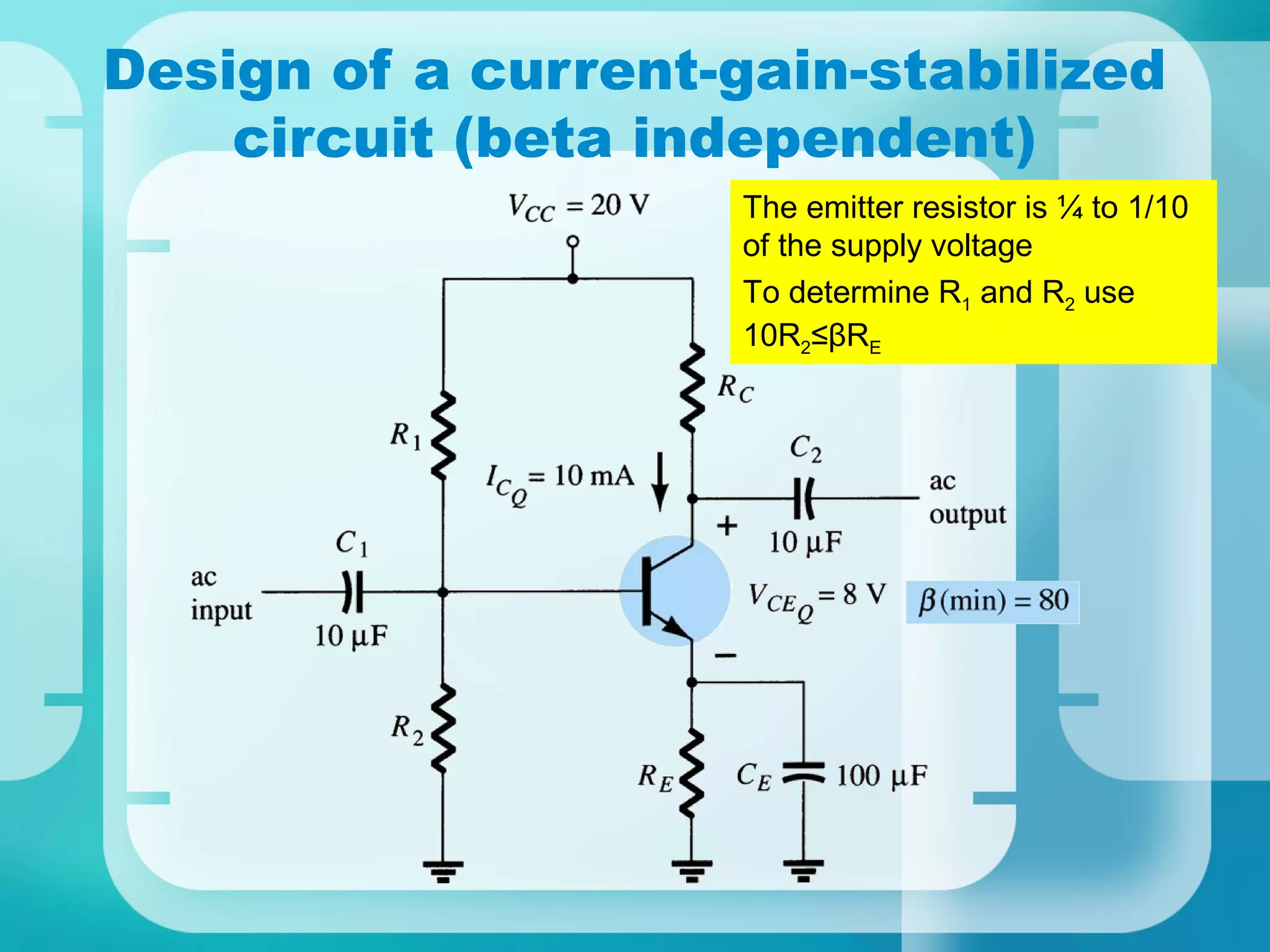
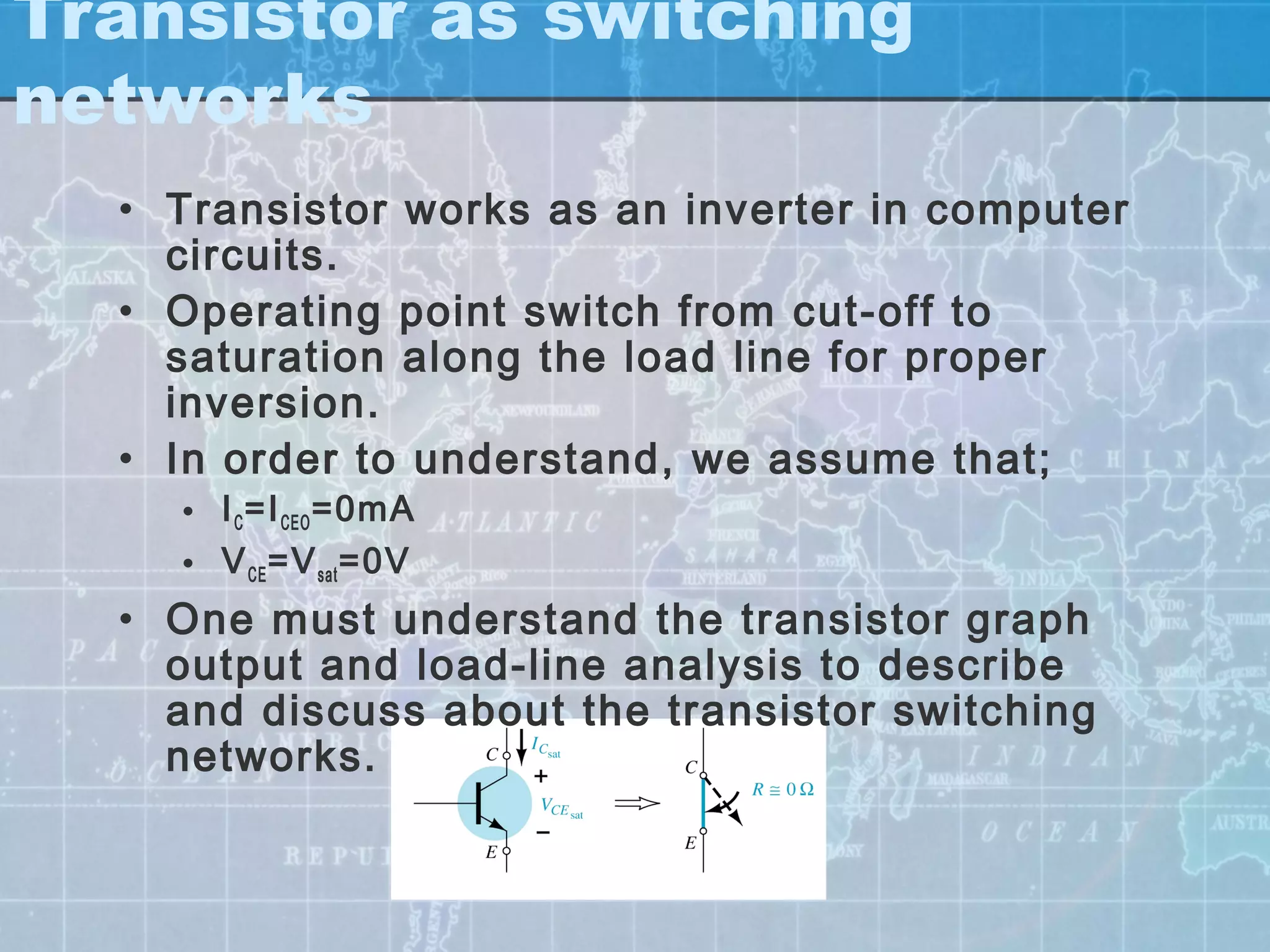
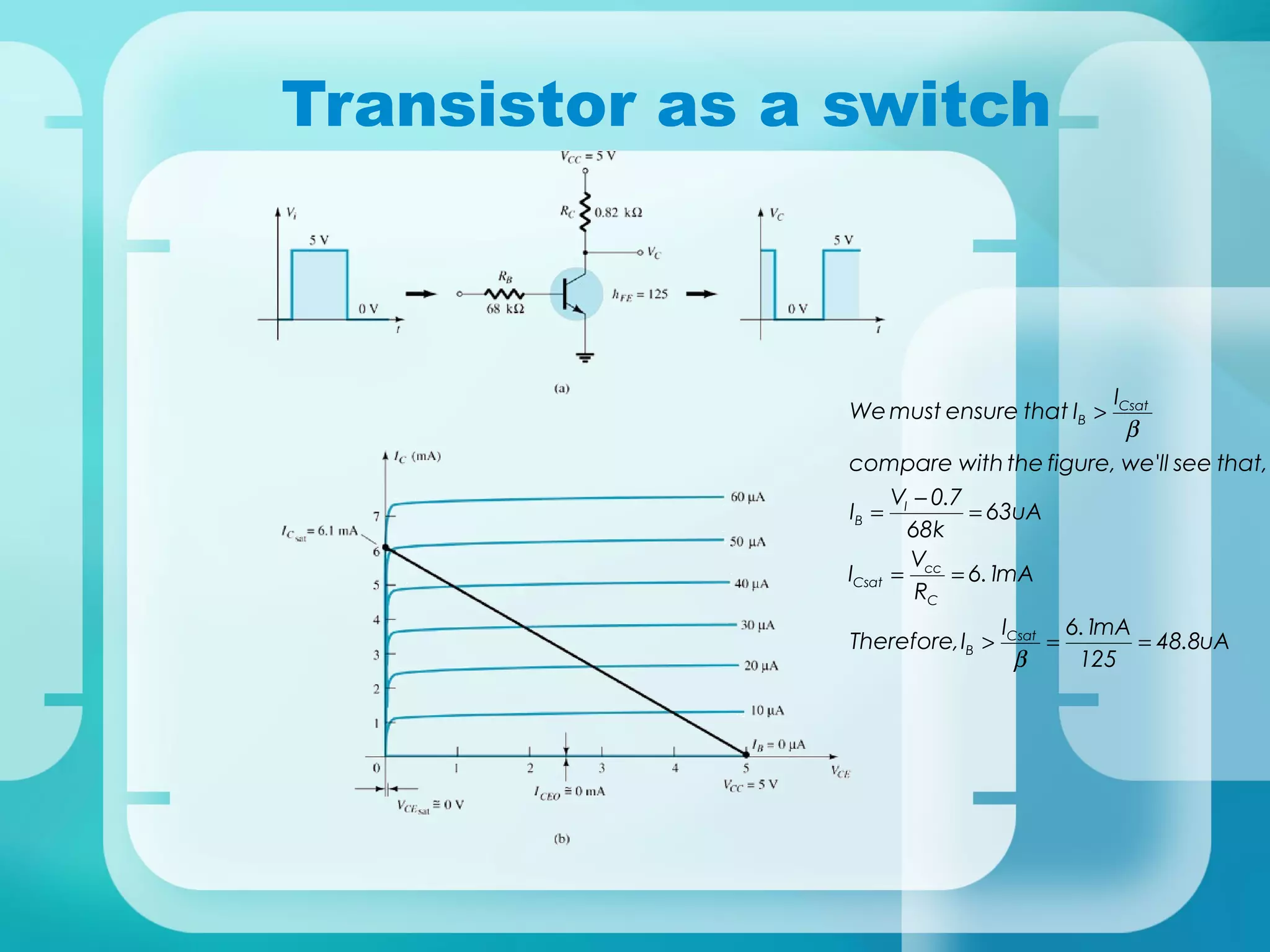
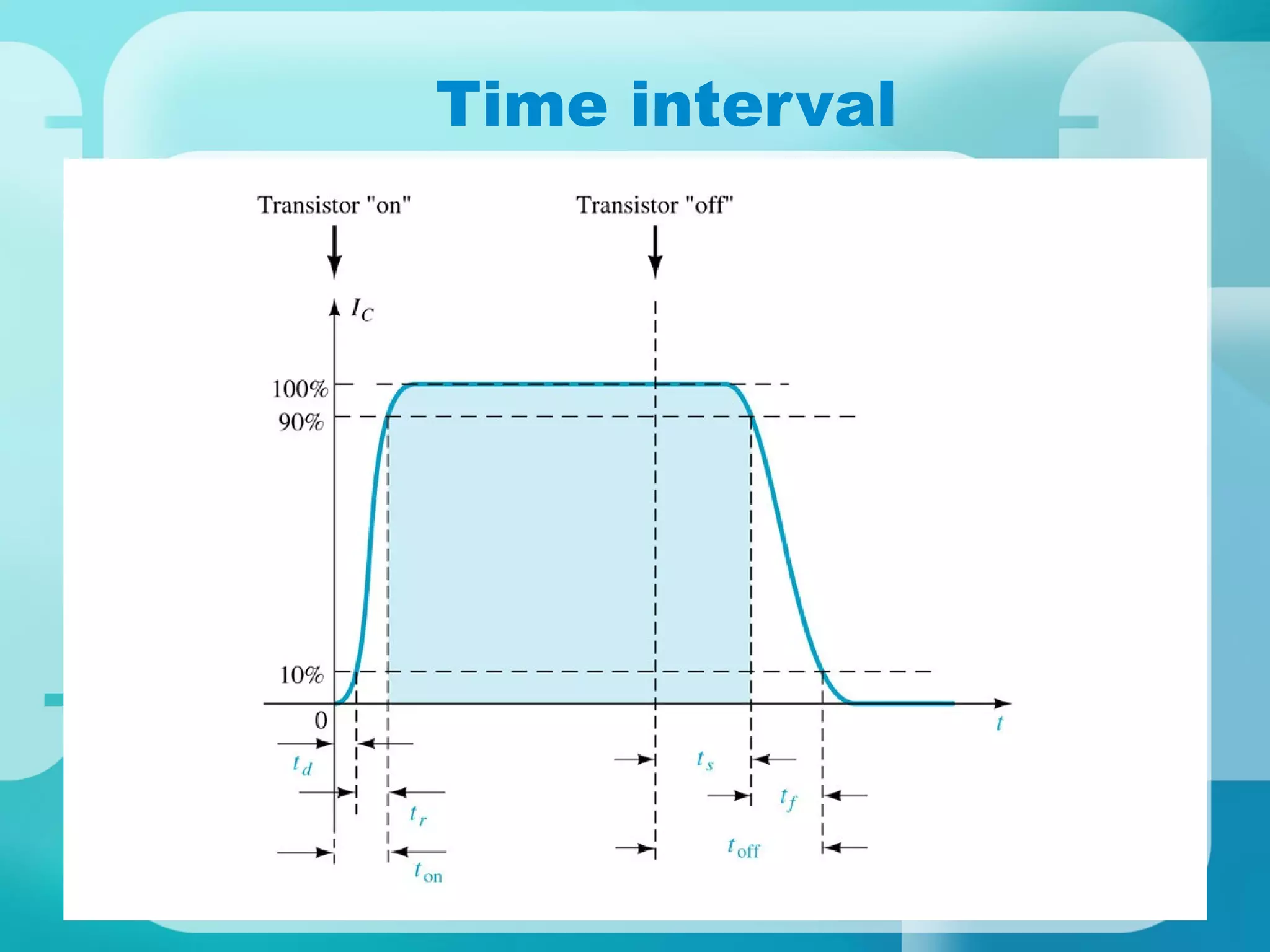
Here are the key steps to analyze the emitter-stabilized bias circuit:
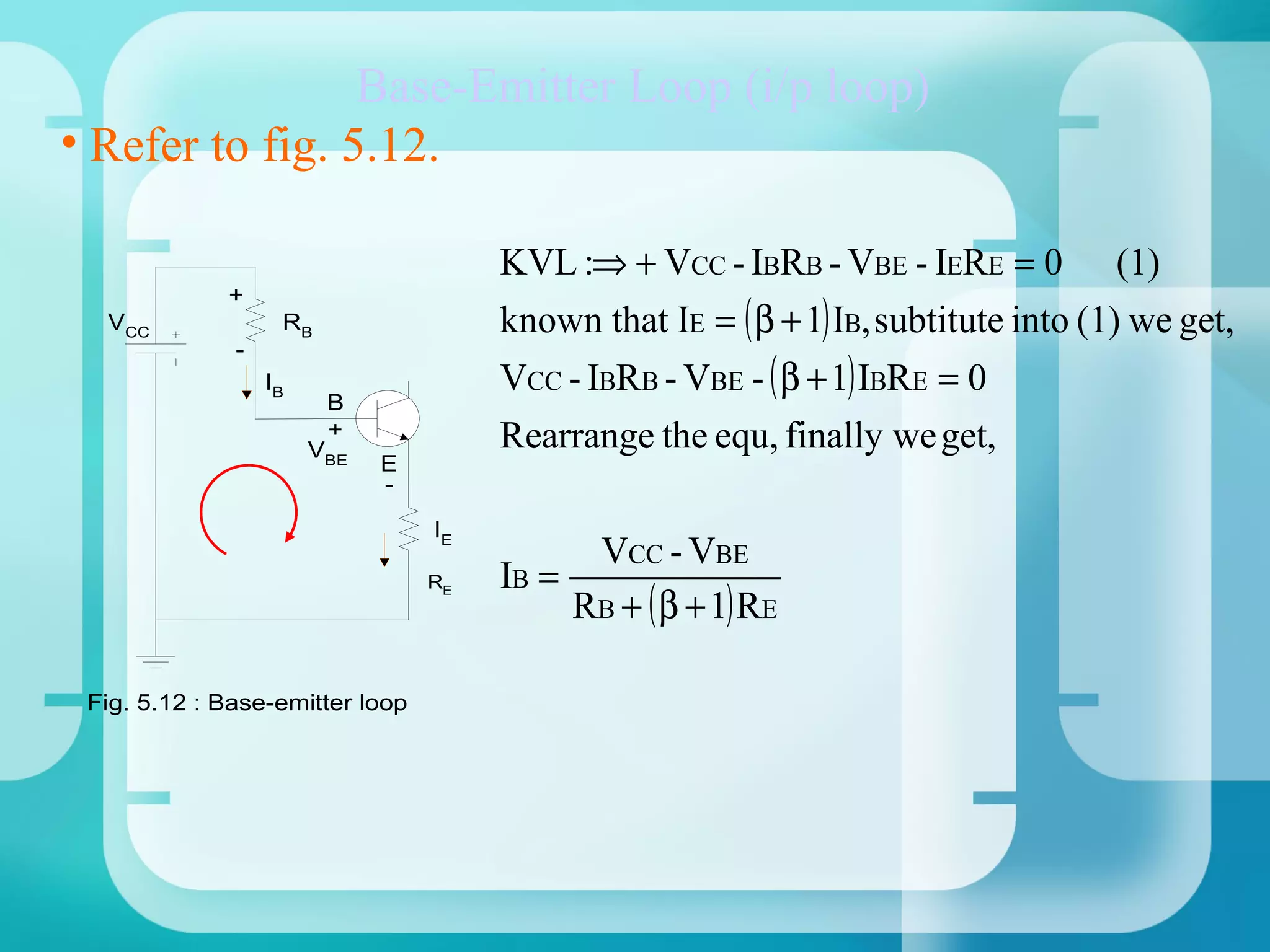
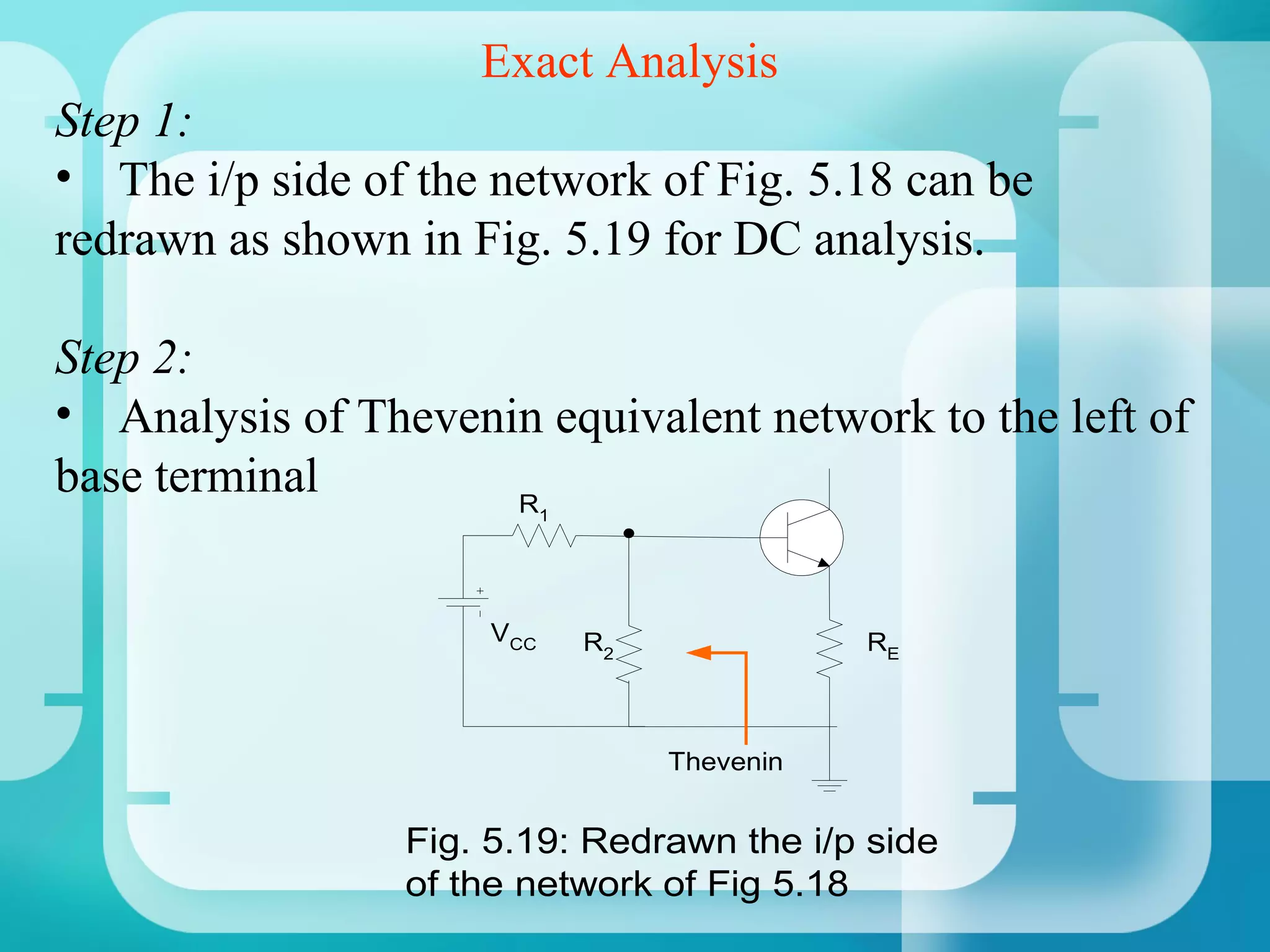
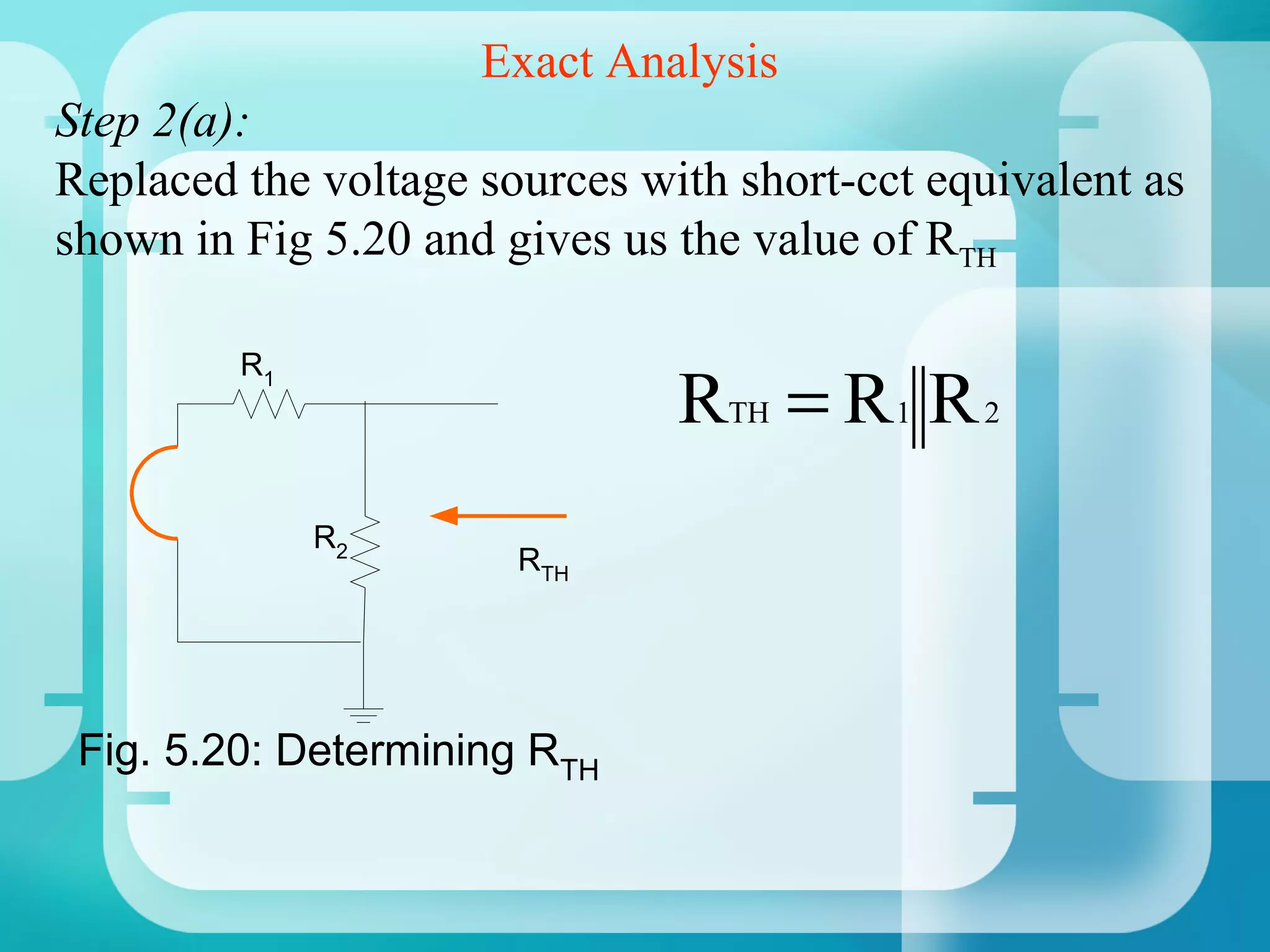
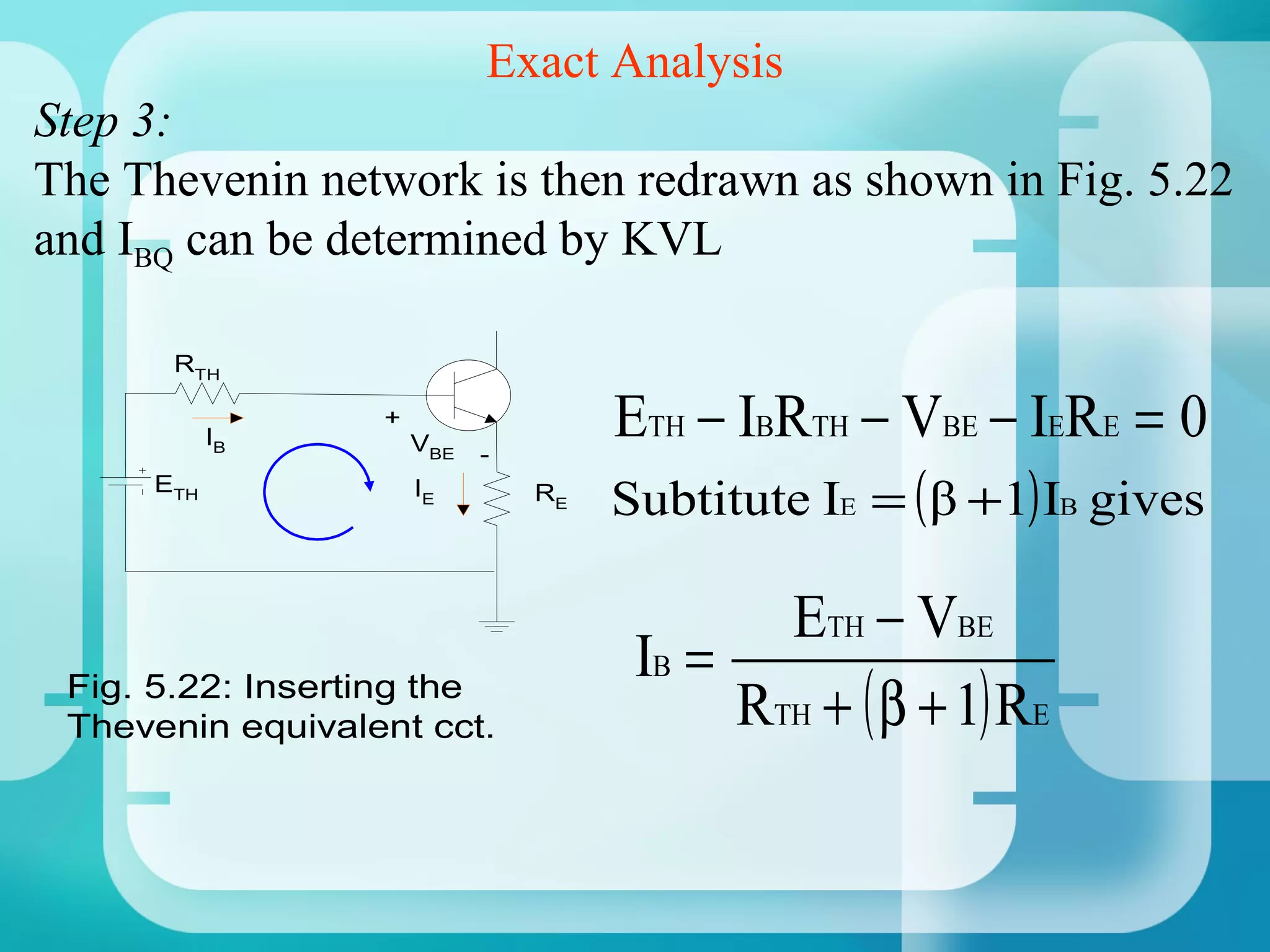
1. Analyze the base-emitter loop using KVL:
VCC - IBRE - VBE - IERE = 0
2. Solve for IB and substitute into IE = βIB
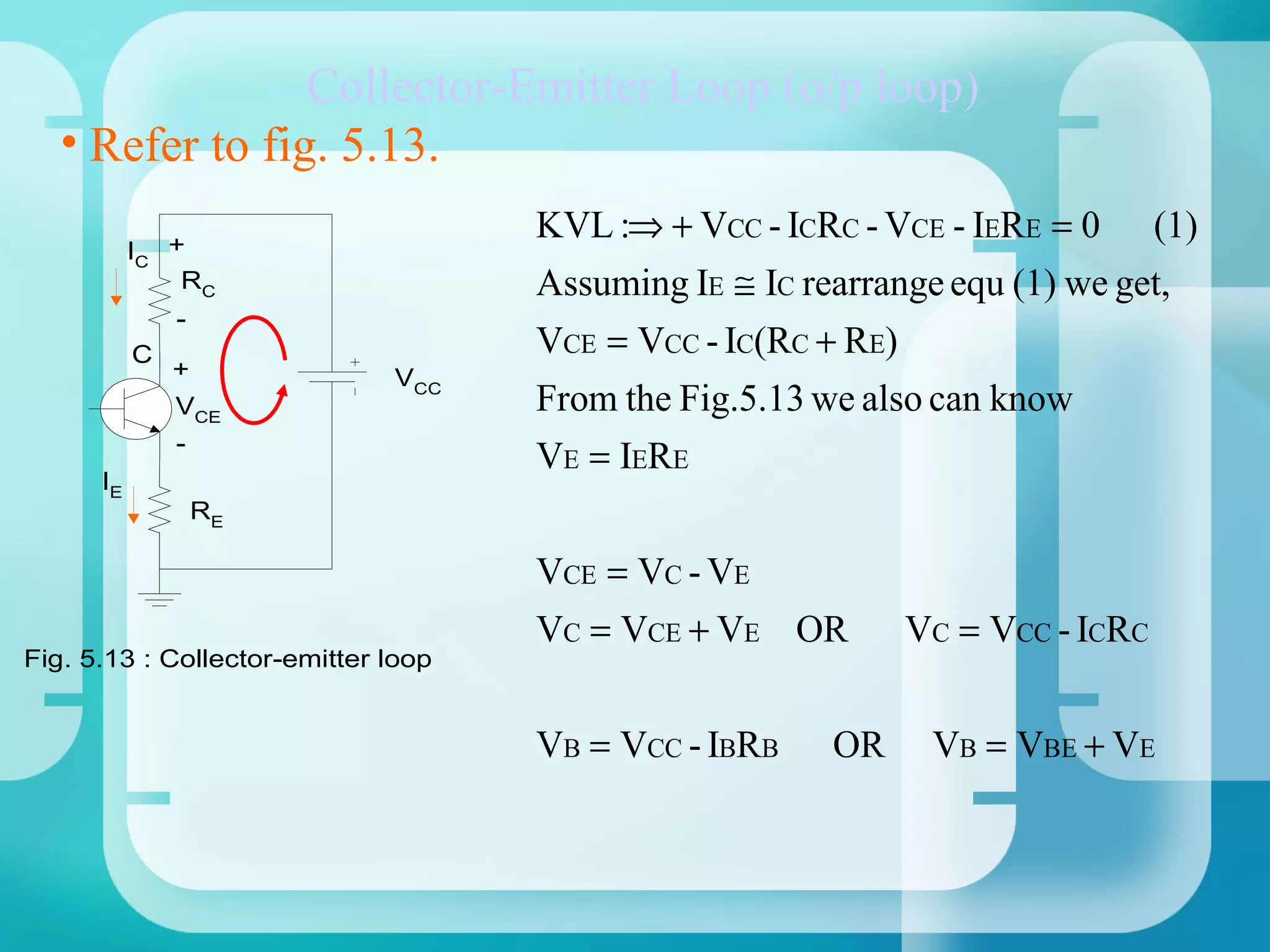
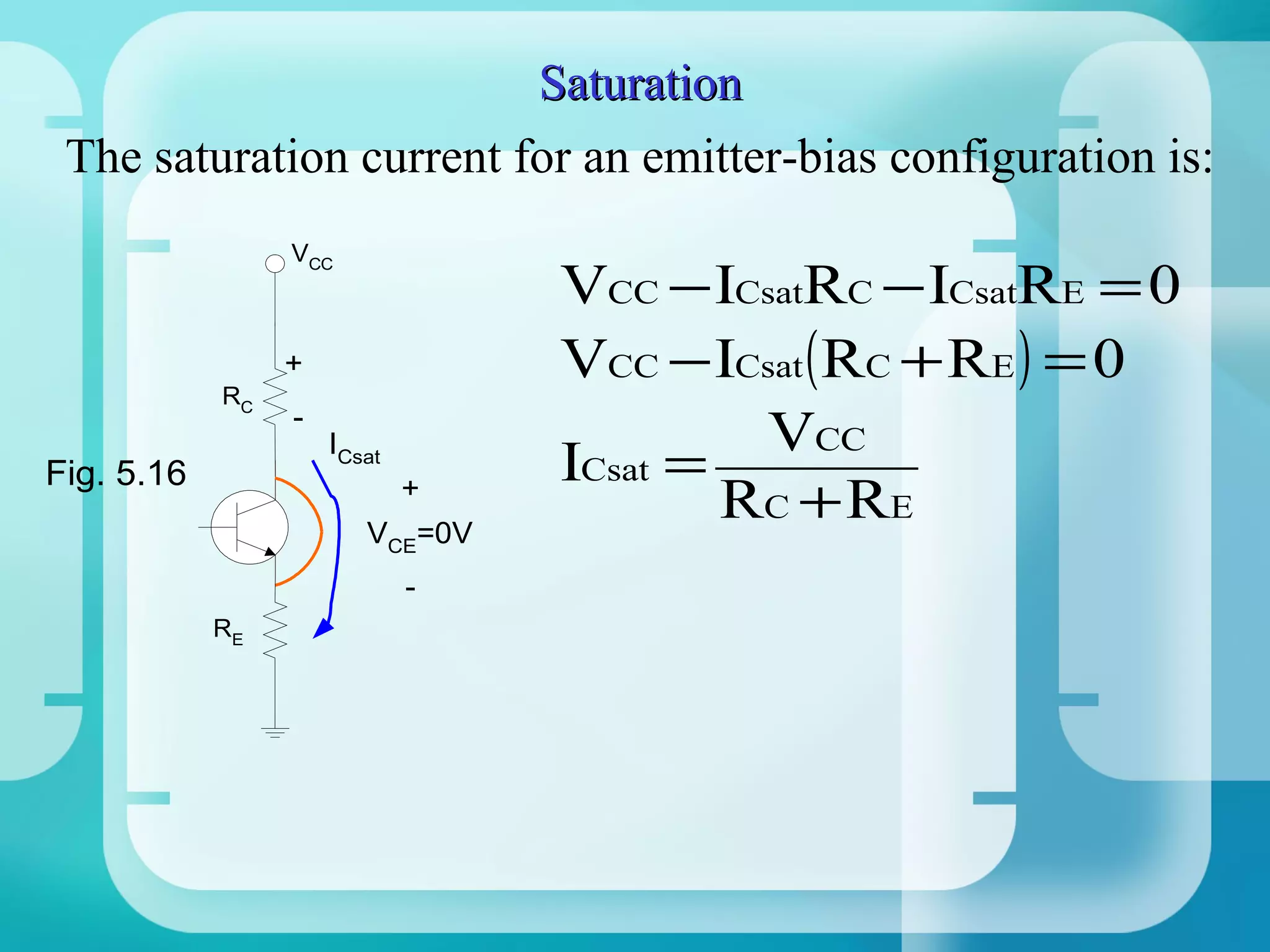
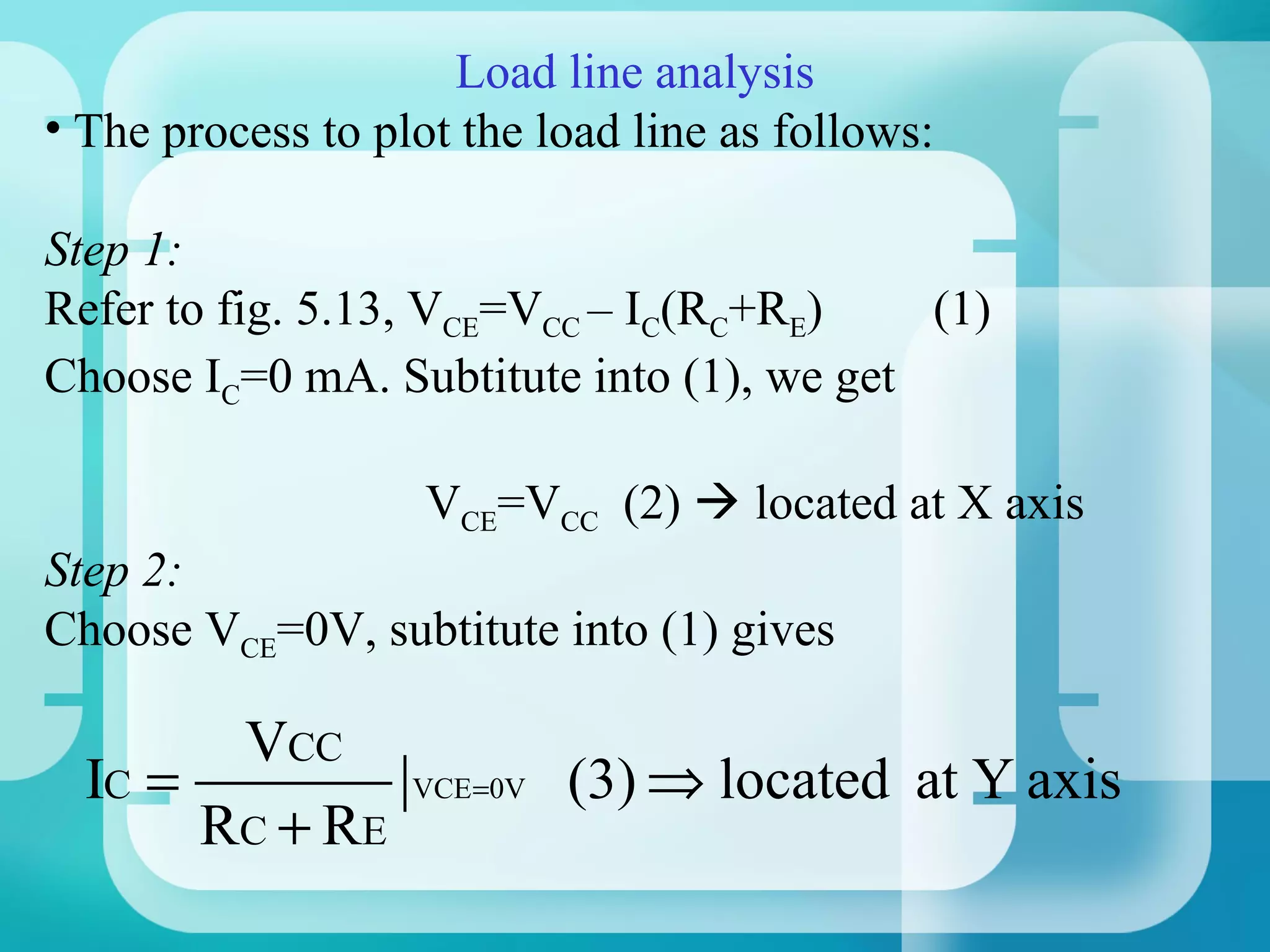
3. Analyze the collector-emitter loop using KVL:
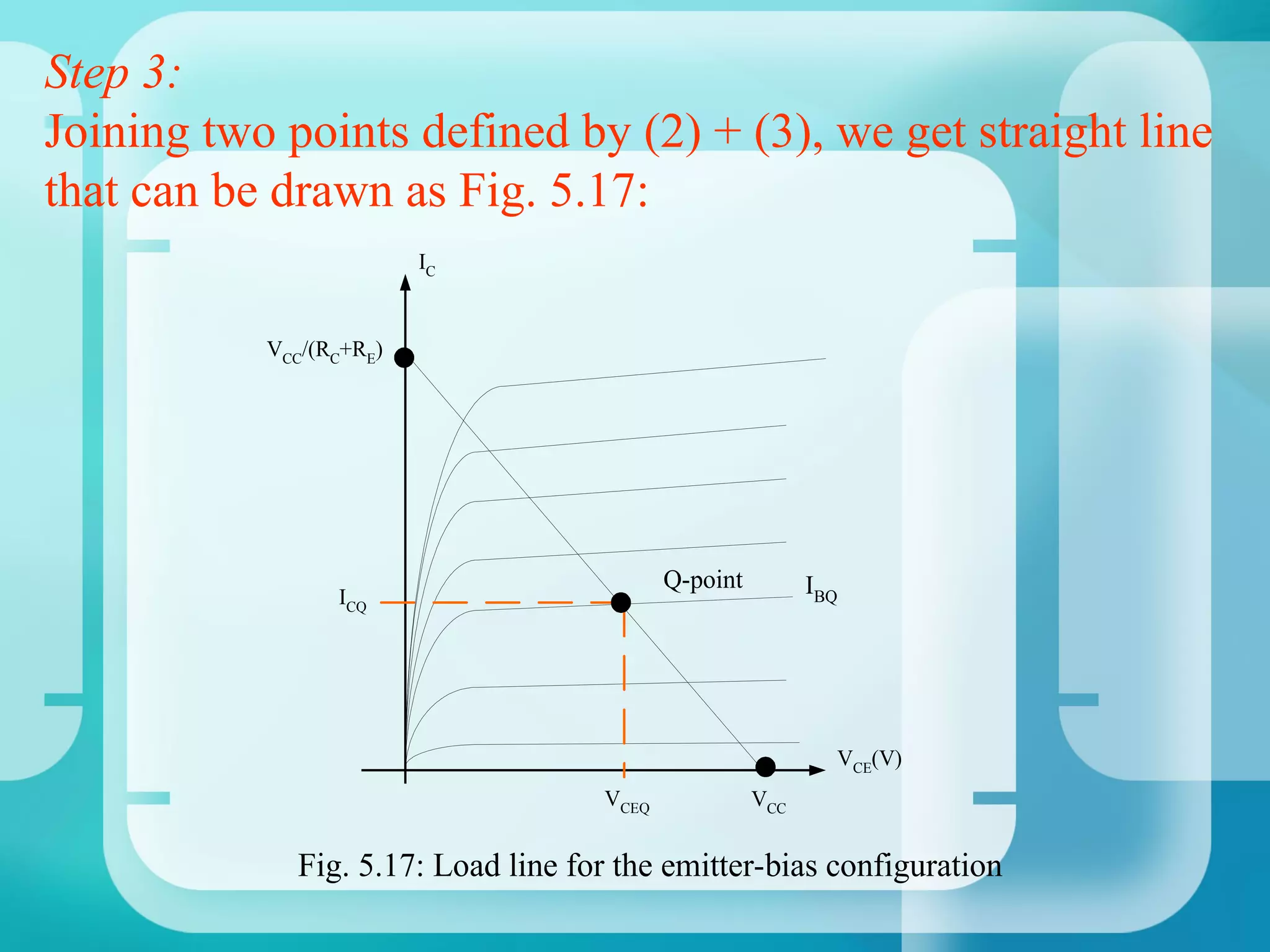
VCC - IC(RC + RE) - VCE = 0
4. Solve simultaneously with the base-emitter loop equation to find Q-point values of IB, IC, VBE, VCE.
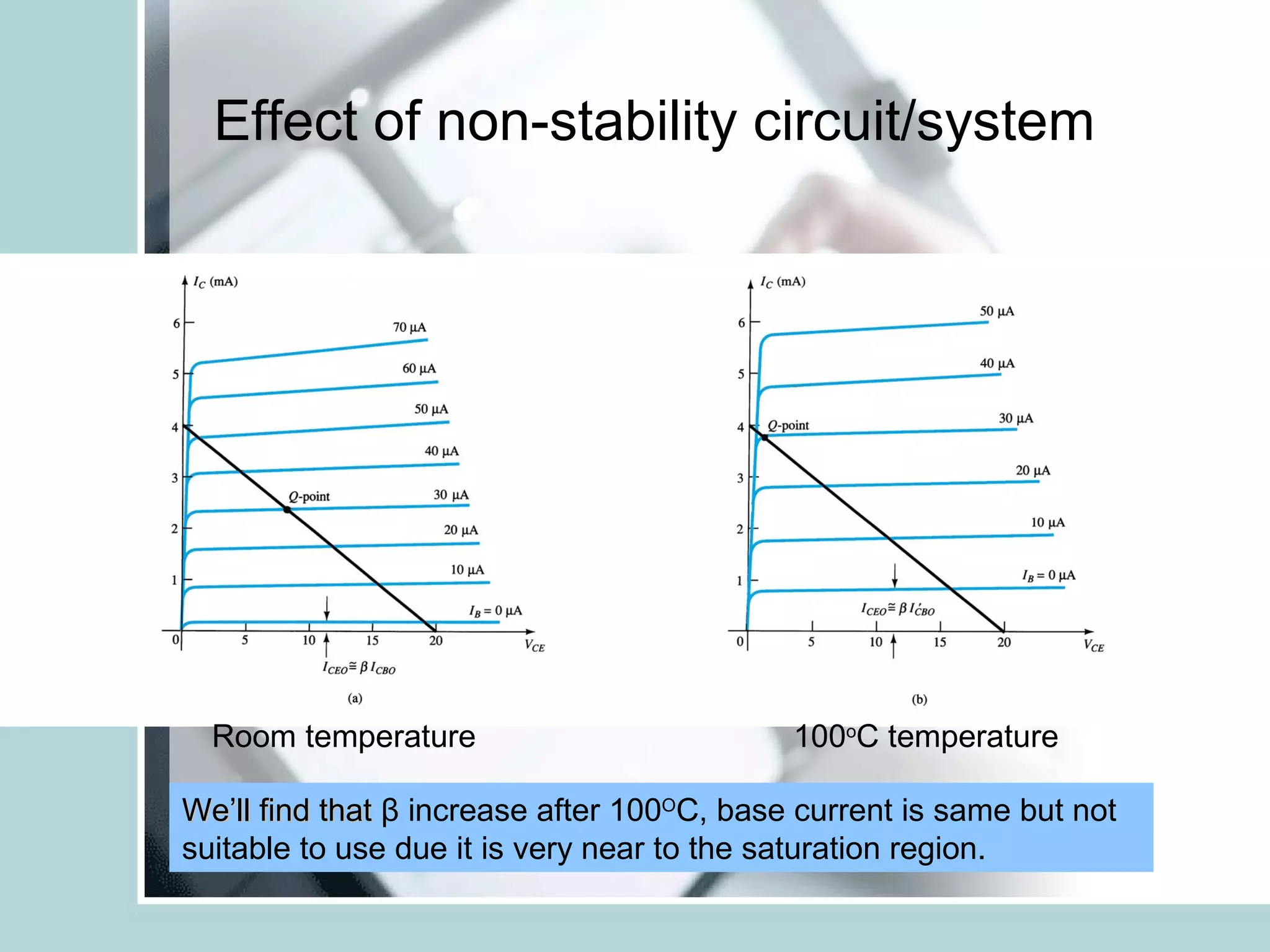
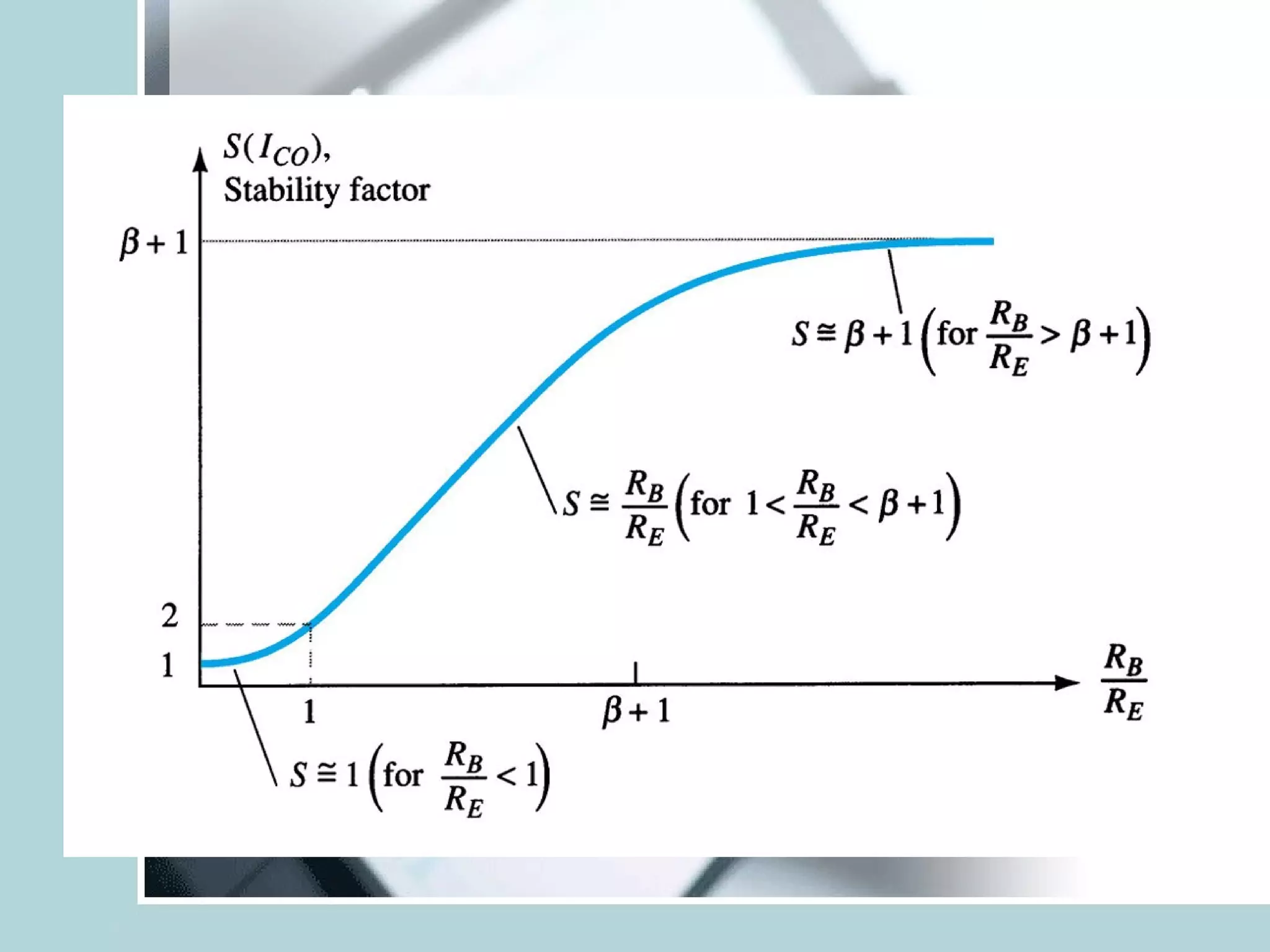
The addition of the emitter resistor RE provides negative feedback which helps stabilize the operating point against variations in β and temperature. This makes the