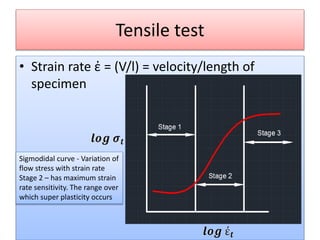
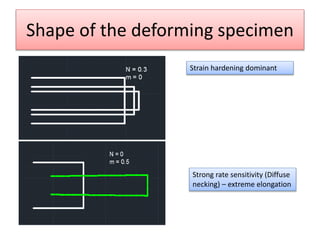
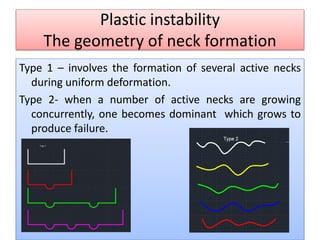
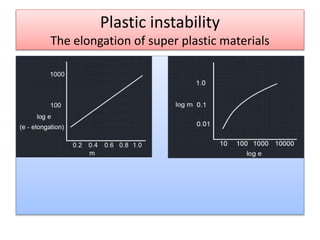
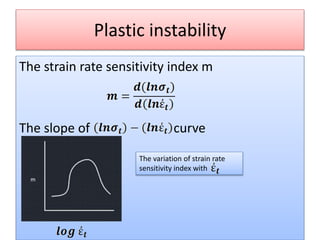
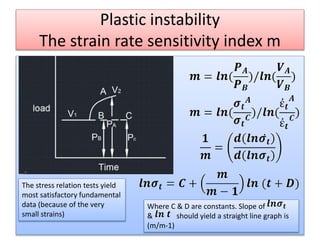
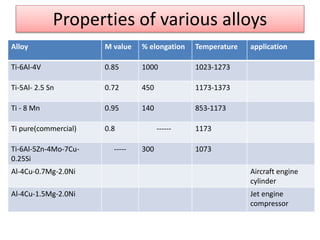
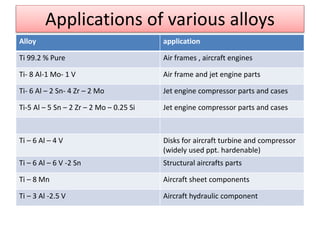
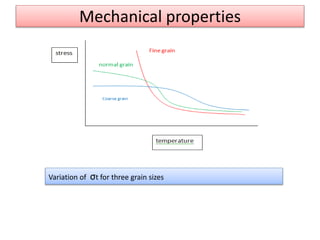
This document discusses super plasticity, which is a deformation process that produces high elongations in metallic materials during tension testing. For super plasticity to occur, the material must have an ultra fine grain size and be deformed at a temperature greater than or equal to 0.4 times the absolute melting point. The document outlines various constitutive relationships that describe super plastic deformation and discusses factors that influence strain rate sensitivity. It also examines conditions necessary for super plastic forming and methods for producing ultrafine grain sizes in materials.

1. Super Plasticity
Dr.R.Narayanasamy,
Professor,
Department of Production Engineering,
National Institute of Technology, Tiruchirappalli – 620 015.
Tamil Nadu, India

2. Super Plasticity
• It is a deformation process that produces essentially
neck-free elongations of many hundreds of percent in
metallic materials in tension.
(Or)
• It is a deformation process which produce neck free
high elongation in tension.
For super plasticity, the material should have
a) Stable ultra fine grain size
b) Temperature of deformation greater than or equal to
0.4 Tm (absolute melting point)

3. Constitutive Relationship
Where K and m are constants dependent on
temperature and grain size.
m – strain rate sensitivity
m determines the stability of the flow

4. Tensile test
Where t – true
N – nominal or Engineering

5. Constitutive Relationship
Where K’ and N are strain hardening exponents
m – strain rate sensitivity
For temperature below 0.4 Tm,
M ~ 0, N lies between 0.1 to 0.3
For super plastic deformation, N ~ 0 and m
varies from 0.3 to 0.9

6. Constitutive Relationship
For a linear Newtonian – Viscous material, N=0 and m = 1
For temperature and grain size dependence
Where K – constant
L- Grain size
A – constant varies from 2 to 3
Q – activation energy
R- Boltzmann’s constant
T – absolute temperature

7. Constitutive Relationship
For isothermal deformation
A and B are constants

8. Tensile test
• Strain rate ἐ = (V/l) = velocity/length of
specimen
Sigmodidal curve - Variation of
flow stress with strain rate
Stage 2 – has maximum strain
rate sensitivity. The range over
which super plasticity occurs

9. Shape of the deforming specimen
Strain hardening dominant
Strong rate sensitivity (Diffuse
necking) – extreme elongation

10. Plastic instability
The on setting of necking
when m = 0
For plastic stability
and are the incremental changes in true
stress and instantaneous cross sectional area.
Neglecting second order terms, we get

11. Plastic instability
For constant volume principle
For stability
Instability starts when

12. Plastic instability
For linear Newtonian Viscous material, (N=0 and
m=1)
Where

13. Plastic instability
For this material the rate of loss of area at any
cross section is dependent only on the load
and is independent of the cross sectional area

14. Plastic instability
Partial derivatives are coefficients which depends
on specimen history.
The flow is stable δA doesn’t increase with
deformation.
For stability
.
Stability criterion

15. Plastic instability
When m >0.5, there is no necking
For super plastic materials m varies from 0.3 to
0.9 and N~0.
We know that,

16. Plastic instability
When m increases from 0.3 to 0.9, (1-m)/(m)
decreases from 2.33 to 0.11
As m = 1, the dependence of dA/dt on A
decreases.
The extreme elongation for super plastic
materials is the result of the very high
resistance to neck growth.

17. Plastic instability
The geometry of neck formation
Type 1 – involves the formation of several active necks
during uniform deformation.
Type 2- when a number of active necks are growing
concurrently, one becomes dominant which grows to
produce failure.

18. Plastic instability
The elongation of super plastic materials
Take β=0 (because rupture takes place in the
smallest area of cross section)

19. Plastic instability
The elongation of super plastic materials

20. Plastic instability
The strain rate sensitivity index m
The slope of curve
The variation of strain rate
sensitivity index with

21. Plastic instability
The strain rate sensitivity index m
The stress relation tests yield
most satisfactory fundamental
data (because of the very
small strains)
Where C & D are constants. Slope of
& should yield a straight line graph is
(m/m-1)

22. Physical significance of m value
The disagreement in them value (by various
methods) is due to:
a) Necking.
b) The difference in the defect structure because of
various strain employed.
c) A wide variation in m value over the strain rate.
d) Grain growth.
e) The sign and the magnitude of the strain rate
change involved.

23. Properties of various alloys
Alloy M value % elongation Temperature application
Ti-6Al-4V 0.85 1000 1023-1273
Ti-5Al- 2.5 Sn 0.72 450 1173-1373
Ti - 8 Mn 0.95 140 853-1173
Ti pure(commercial) 0.8 ------ 1173
Ti-6Al-5Zn-4Mo-7Cu-
0.25Si
----- 300 1073
Al-4Cu-0.7Mg-2.0Ni Aircraft engine
cylinder
Al-4Cu-1.5Mg-2.0Ni Jet engine
compressor

24. Applications of various alloys
Alloy application
Ti 99.2 % Pure Air frames , aircraft engines
Ti- 8 Al-1 Mo- 1 V Air frame and jet engine parts
Ti- 6 Al – 2 Sn- 4 Zr – 2 Mo Jet engine compressor parts and cases
Ti-5 Al – 5 Sn – 2 Zr – 2 Mo – 0.25 Si Jet engine compressor parts and cases
Ti – 6 Al – 4 V Disks for aircraft turbine and compressor
(widely used ppt. hardenable)
Ti – 6 Al – 6 V -2 Sn Structural aircrafts parts
Ti – 8 Mn Aircraft sheet components
Ti – 3 Al -2.5 V Aircraft hydraulic component

25. Mechanical properties
Variation of σt for three grain sizes

26. Mechanical properties
• Region II with (m> 0.3)
over which super
plasticity occurs .
• Beyond ϵ̇* , m decreases.
• II a region over which an
optimal super plasticity
deformation occurs . The
material exhibits work
hardening .
• II b decreases with increase ϵ̇t
Region/Range in which super plasticity is slowly being
lost .

27. Necessary condition for super plastic
forming
1. Duplex and multiphase structure (which have
stable grain size and resistance to grain
growth)
2. The type of phase or phase and their
distribution .
3. The grain boundary condition .
4. Temperature , strain rate and grain size .
Above condition influence the degree of super
plasticity .

28. Necessary condition for super plastic forming
5. Lower the eutectic (or equivalent)
temperature , better the super plasticity
properties .
6. Ternary eutectics are more super plastic than
binaries .
7. Strain rate should match the velocity of
diffusion processes . This improves the super
plasticity .

29. Necessary condition for super plastic
forming
8. Coarse grained structure and dissolved
second phase – eliminates strain rate
sensitivity (m) and high elongation .
9. non-deformable second phase particle found
in dispersion hardening alloys- eliminates the
effect of fine grain size and lead to cavitation .
10. Undissolved carbides (martensite in Fe-C
system ) prevent superplasticity .

30. Production of ultrafine grain size
1. Cold/hot work the commercial pure metal
and produce fine grain sizes stabilize the
grain sizes by dispersion of impure
particles which pin the grain boundaries
predominantly .

31. Production of ultrafine grain size
2 . When the alloy contains second phase particles
• We know that
where R= radius of grain
r= radius of second phase particle
f= volume fraction of second phase
particle

32. Production of ultrafine grain size
2 . When the alloy contains second phase particles
• The above relation shows that the minimum
grain size that can be obtained depends on
a) A smaller “r”
b) More “f ”(high f)
when second phase particle are present , the
grain boundary area is eliminated (where the
boundary intersects the particle) . This leads
to a decrease in the grain boundary energy .

33. 2 . When the alloy contains second
phase particles
When the decrease in grain boundary energy
is more , the system results in grain growth .
(this is structural super plasticity)
Zr addition in Al alloys is helpful .

34. Production of ultrafine grain size
3. (a). cast alloys of eutectic/eutectoid or poly
phase
(b). Work them by about 60-70% to get an
intimate mixture of phases .
(c). Stable ultra fine grains of less than 10 µm.
can be obtained when particles are relatively
coarse and well separated .
This is extensively employed
ex. Zn-Al , Al-Cu

35. Production of ultrafine grain size
For Ni base super alloys
• Power metallurgy route because of several
advantages .
• Segregation and bonding makes unsuitable in
conventional method .
a) Compact alloy powder (after mixing)
b) Hot extrude
grain refinement is obtained
spinodal decomposition

36. Production of ultrafine grain size
Variable of deformation
a) Strain rate
uniform strain and secondary creep rate
increases with decrease in grain size .
where L = grain size
b = constant varies from 2 to 3

37. Production of ultrafine grain size
Variable of deformation
• Increase in strain rate beyond ϵ̇t , is equivalent
to increases in the grain size which has a
deleterious effect on super plasticity .
• The strain rate increases exponentially with
temperature .

38. Production of ultrafine grain size
Variable of deformation
Strain
i. Finer grain material exhibits greater recovery
σI = stress at zero strain for a given strain
rate
α =slowly varies with strain rate
ii. Super plastic deformation is essentially strain
independent when structural changes are
absent .

39. Production of ultrafine grain size
Strain rate sensitivity index “m”
1. m increases with decreasing grain size
2. m increases with increasing temperature
3. In many alloy system
maximum value of ‘m‘ is reached at a
temperature just below the phase boundary
defining the upper limit of the two phase
field .

40. Production of ultrafine grain size
Strain rate sensitivity index “m”
4. The temperature dependence of ‘m’ is more
in region II compared with region I or III .
5. ‘m’ is independent of strain rate and
dependent of temperature
ex. Zn-Al eutectoid alloy.

41. Reference book
• K. A. Padmanabhan, Davis , Super plasticity .

42. Thank you