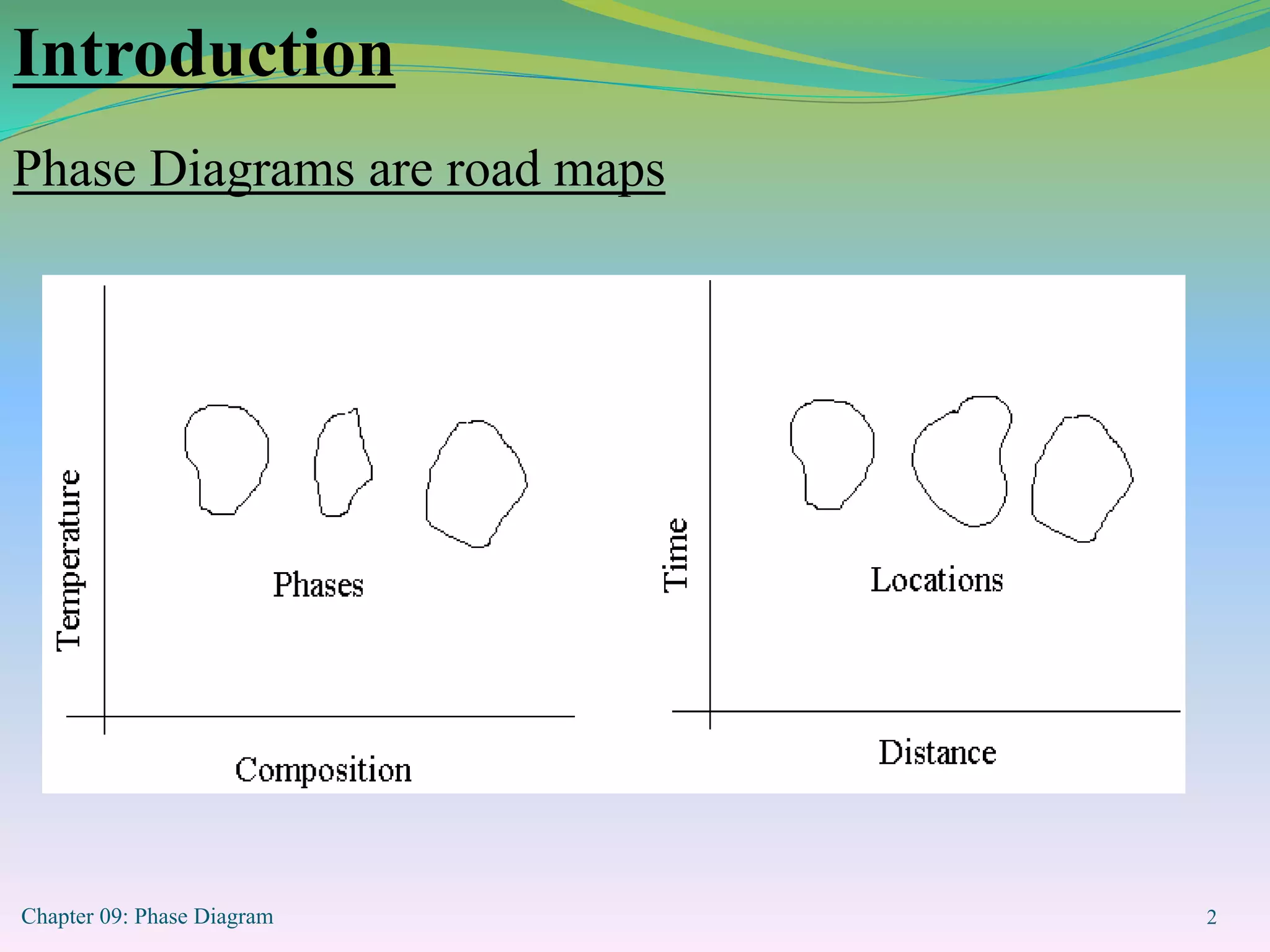
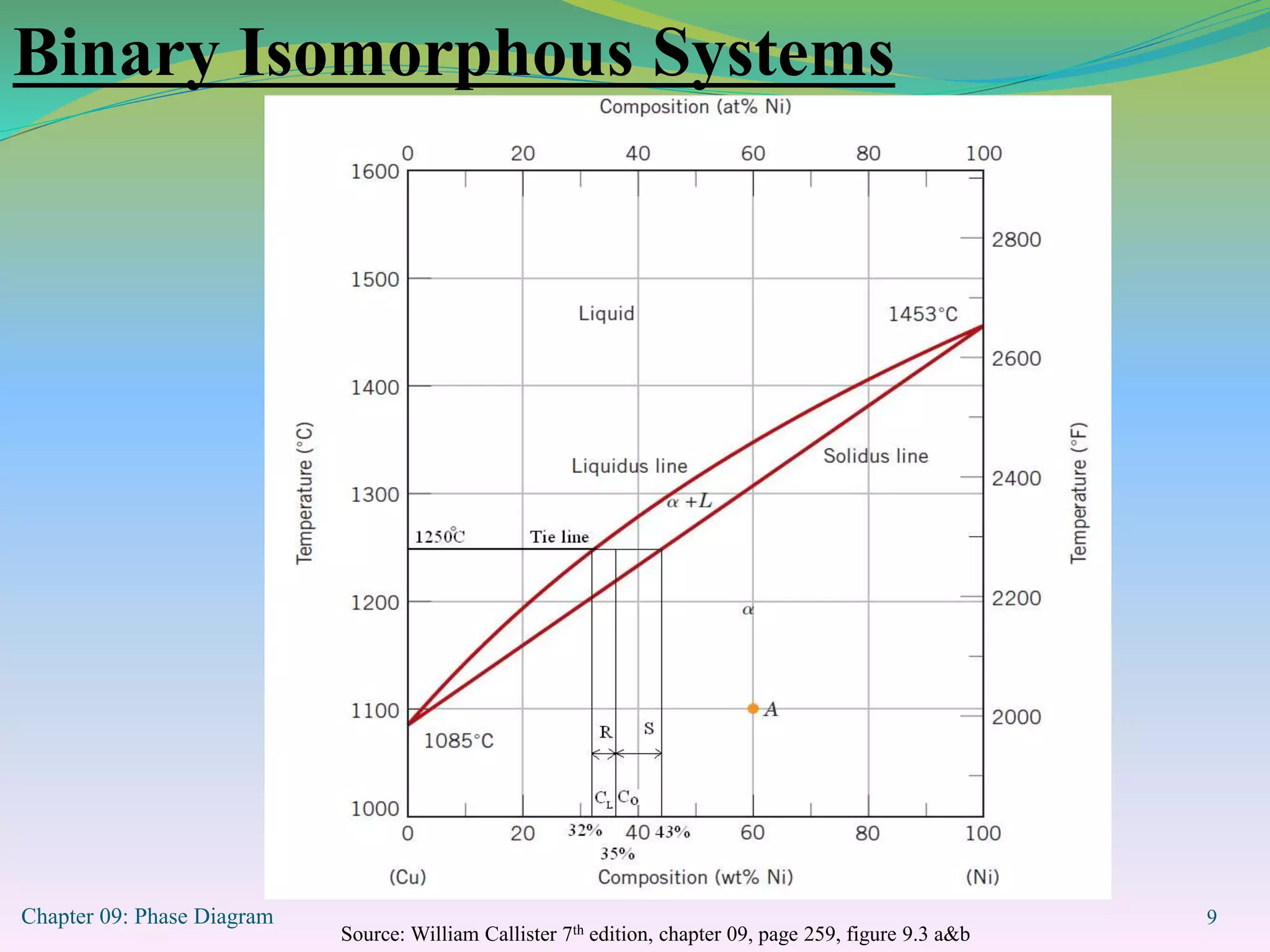
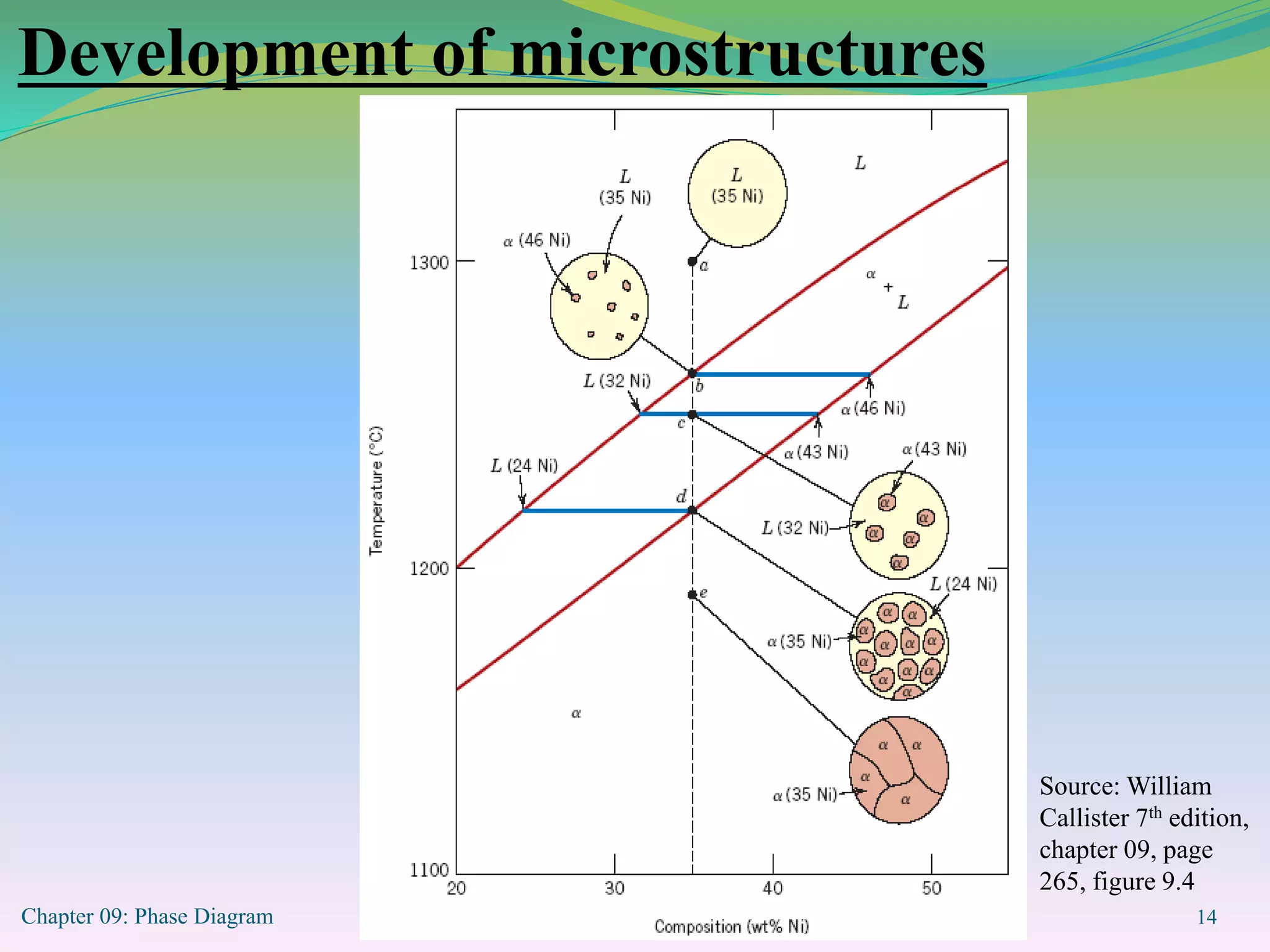
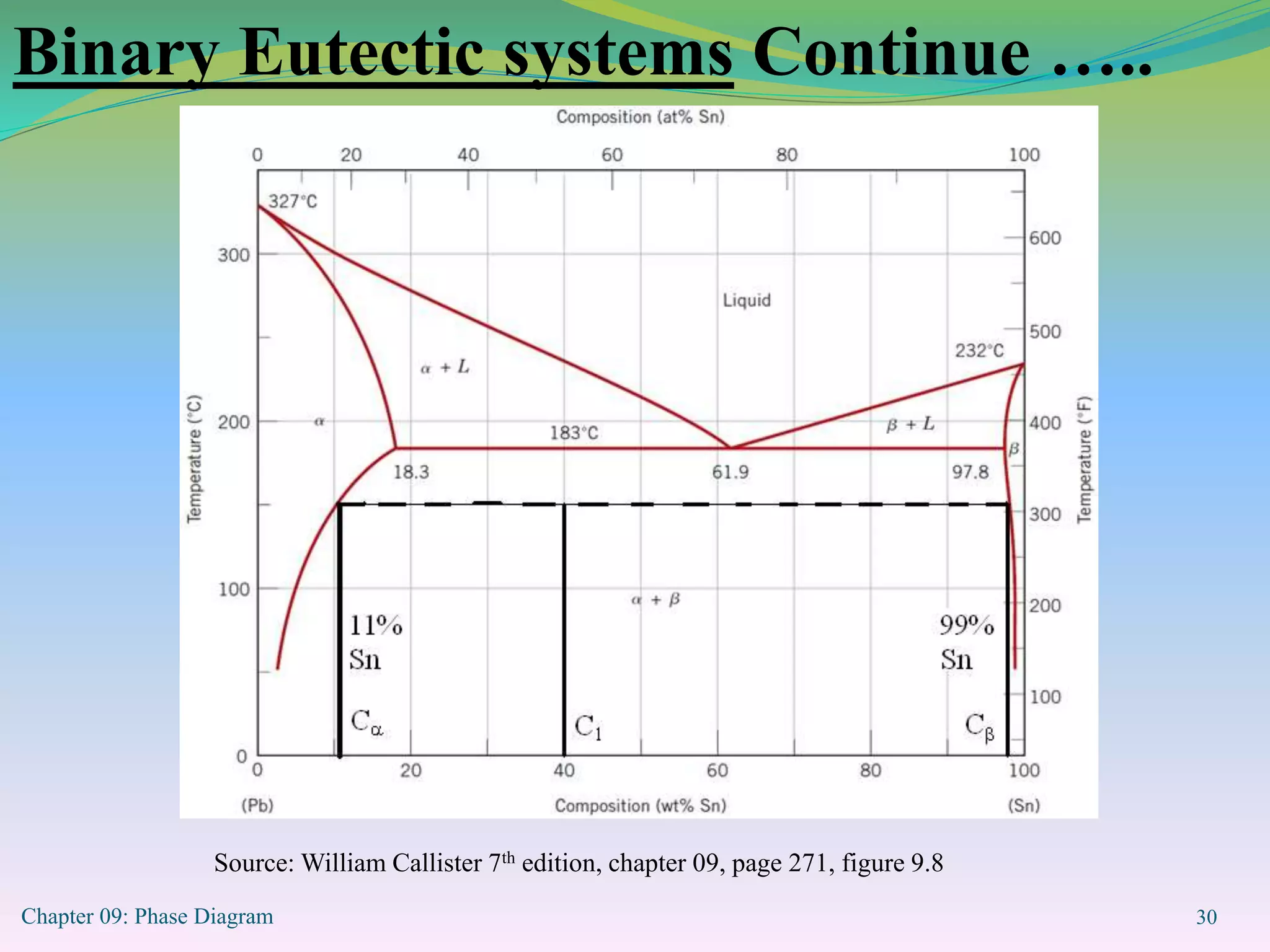
This document discusses phase diagrams and binary alloy systems. It defines key terms like phase, solubility limit, and equilibrium. It describes two main types of binary alloy systems - isomorphous systems which have complete solubility, and eutectic systems which have a eutectic point. For isomorphous systems, it discusses microstructure development and how properties vary with composition. For eutectic systems, it outlines the phase diagram features and eutectic reaction. It also provides an example problem calculating phase amounts in the Pb-Sn system at a given temperature and composition.