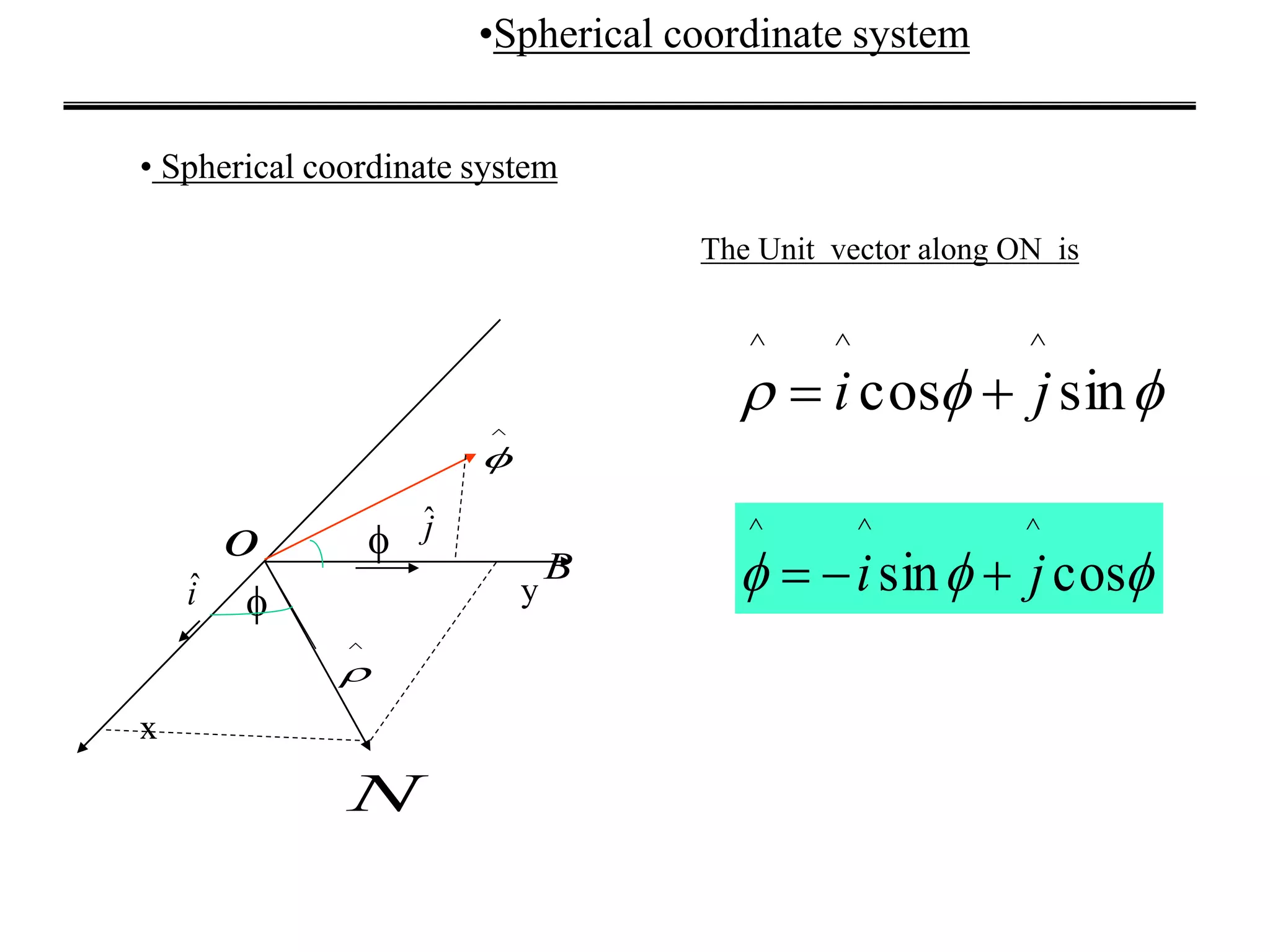
This document discusses velocity and acceleration in different coordinate systems, including Cartesian, spherical, and cylindrical coordinates. It provides the equations to calculate velocity and acceleration vectors in each system. In spherical coordinates, it defines the radial, angular, and azimuthal positions and shows how to write the position, velocity, and acceleration vectors in terms of these variables. Similarly, it defines the radial, angular, and vertical positions in cylindrical coordinates and gives the corresponding equations for velocity and acceleration.

2. B.Sc.-I (Physics)
Paper-I, Unit 01
Dr. Krishna Jibon Mondal
Assistant Professor and Head
Department of Physisc and Electronics
Shri Shankaracharya Mahavidyalaya, Bhilai
Part 01
Velocity and Acceleration in Different Co-ordinates system

3. Outlines
1. Inertial and Non Inertial frame
2. The Cartesian (rectangular)
coordinate system
3. The spherical coordinate system
4. The cylindrical coordinate system

5. Inertia and non-inertia of Frames

6. Cartesian coordinate system
In Cartesian coordinates system, the position of any particle can be represented
by (x,y,z) along the rectangular axis X,Y,Z. If the unit vector along the these axis
are i,j,k respectively then the position vector P will be
Z
X
Y
P(x,y,z)
B
^^^
kzyjixr 

o
c
N
A
k
t
z
j
t
y
i
t
x
v ˆˆˆ









kvjvivv zyx
ˆˆˆ 
t
v
a



)ˆˆˆ( kvjviv
t
a zyx 



)ˆˆˆ k
t
v
j
t
v
i
t
v
a zyx









)ˆˆˆ( kajaiaa zyx 

7. Spherical coordinate system
In Spherical coordinates system, the position of any particle P can be represented
by (r, , ) where r is radial,  is angular momentum and  is azimuthal position
x
y
z
P(x,y,z)
A


^
r
^

^^^
kzyjixr 

 cossincos rONOAx 
 sinsinsin rONOBy 
cosrOCz 
The position vector of point P is
^^^
cossinsincossin krjrirr  

^^^
cossinsincossin kji
r
r
r  
o
N
B
c

 rrr
^

 rrr
^
ˆ
^

ˆ

8. Spherical coordinate system
ˆ
^


kˆ
P
The Unit vector along is
)90cos()(cos
^^^
  k
 sinsincoscoscos
^^^^
kji 
 sincos
^^^
ji 
The value of
Then the obtained result will be

9. • Spherical coordinate system
x
y
jˆ

•Spherical coordinate system
^

The Unit vector along ON is
 sincos
^^^
ji 
iˆ
o
N
B  cossin
^^^
ji 
^



10. Spherical coordinate system
^
The Unit vector along is
 sinsincoscoscos
^^^^
kji 



cosˆ
ˆ






cosˆsinˆ
ˆ



r
Then the following relation are obtained
^^^
cossinsincossin kji
r
r
r   

ˆsinsincoscoscos
ˆ ^^^



kji
r




sinˆ)cossin(sin
ˆ
cossinsinsin
ˆ
^^
^^






ji
r
ji
r
 cossin
^^^
ji 
rkji ˆcossinsincossin
ˆ ^^^









cosˆcoscossincos
ˆ ^^



ji

11. Spherical coordinate system
rˆ
ˆ







ˆˆ


r
0
ˆ







sinˆˆ


r



cosˆ
ˆ






cosˆsinˆ
ˆ



r
Then the following relation are obtained

12. Spherical coordinate system
The position vector at point P is expressed as
),(ˆˆ rrrrr 

Then the velocity of a vector is represent as
r
t
r
t
r
r
t
r
v ˆ
ˆ










 rr
t
r
rv ˆ
ˆ






and
),(ˆˆ rr 
t
r
t
r
t
r













 



ˆˆˆ
Then the above equation transform as


ˆˆ


r


sinˆˆ


r

13. Putting all the values we get
 


sinˆˆˆ rrrr
t
r
v 



)cos2sin2sin(ˆ
)cossin2(ˆ)(ˆ 2222
sin







rrr
rrrrrrr
t
v
a








 )cosˆsinˆ(
ˆˆ








r
tt



  cosˆˆ
ˆˆ








r
tt
Putting all the values we get acceleration
as

14. Cylindrical coordinate system
In cylindrical coordinates system, the position of any particle P can be represented
by (r, , z) where r is radial,  is angular momentum and z is vertical position
x
y
z
P(x,y,z)
A


Zˆ
^
r
^

^^^
kzyjixr 

cosrAOx  sinrOBy 
zOCz 
The position vector of point P is
kzjrirOPR ˆˆsinˆcos  

^^
cossinˆ ji  
o
N
B
c
R

r
^
r
22
yxr 
y
x
tan
ji
r
r
r ˆsincos
^^
 
^^
kz 

15. Cylindrical coordinate system
The and are function of and then
Then the velocity of a vector is represent as
)ˆˆ( kzrr
tt
R
v 








t
z
k
t
r
r
t
r
rv








 ˆˆ
ˆ

Putting all the values we get
zkrrrv 
 ˆˆˆ  
and acceleration
zzrrrrr
t
v
a 


ˆ)2(ˆ)(ˆ 2



 
rˆ ˆ ˆ
zˆ
0
ˆˆ






t
k
t
z
kzrrR ˆˆ 

  cosˆsinˆˆ
ji
t
r



 ˆˆ




t
r
ji
r
r
r ˆsincos
^^
 
But we know that
Then we get

16. Thank You