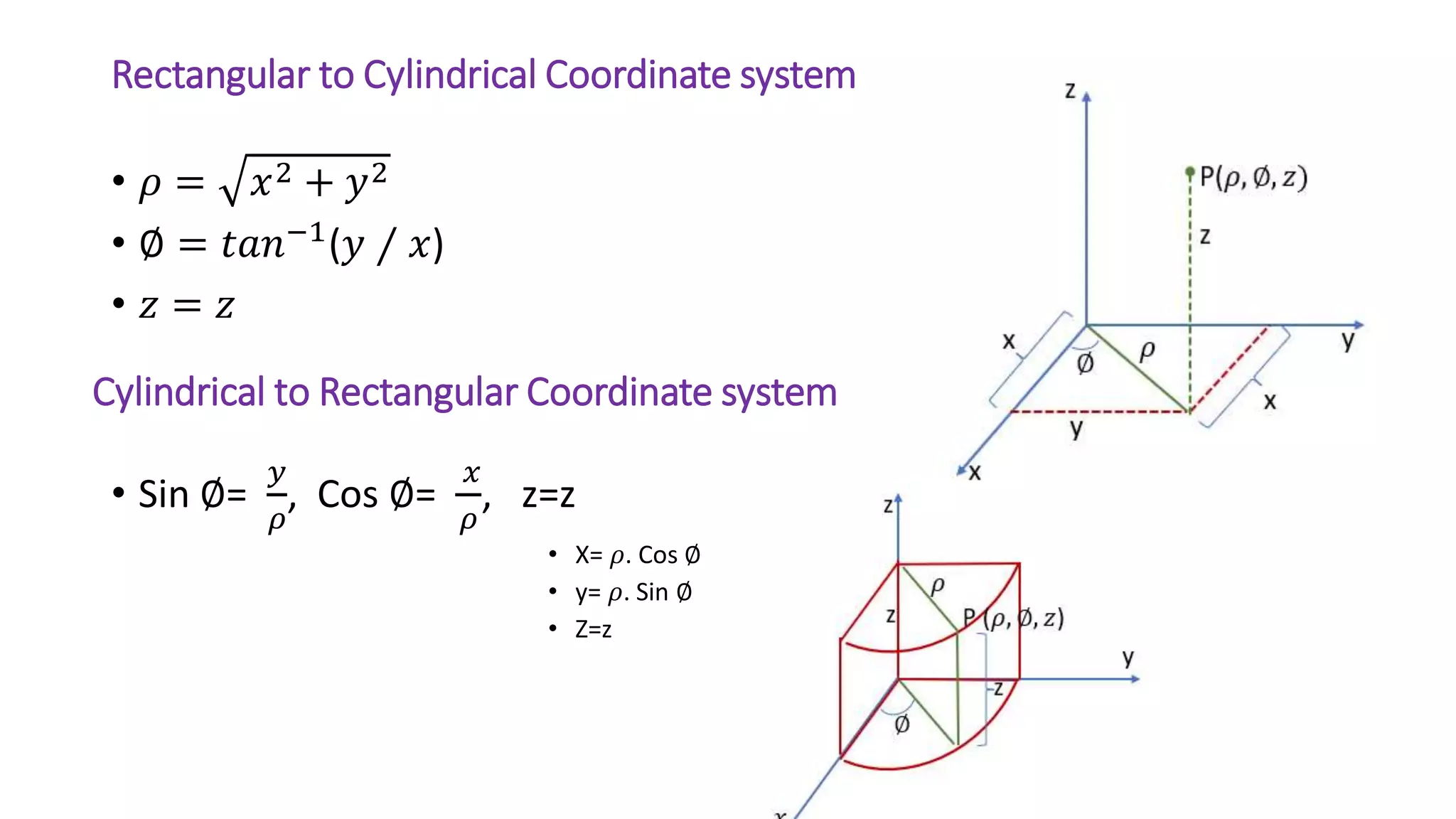
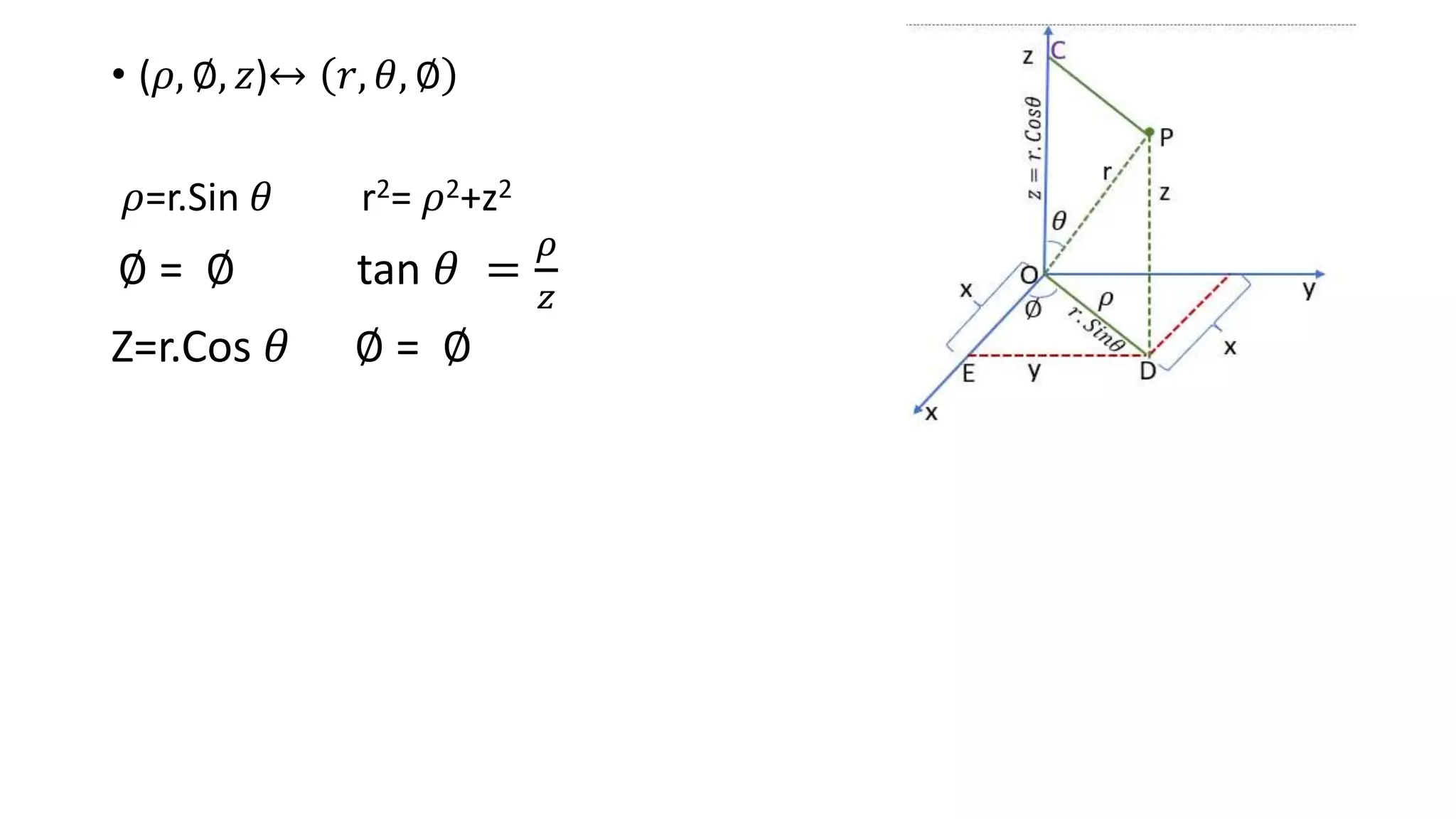
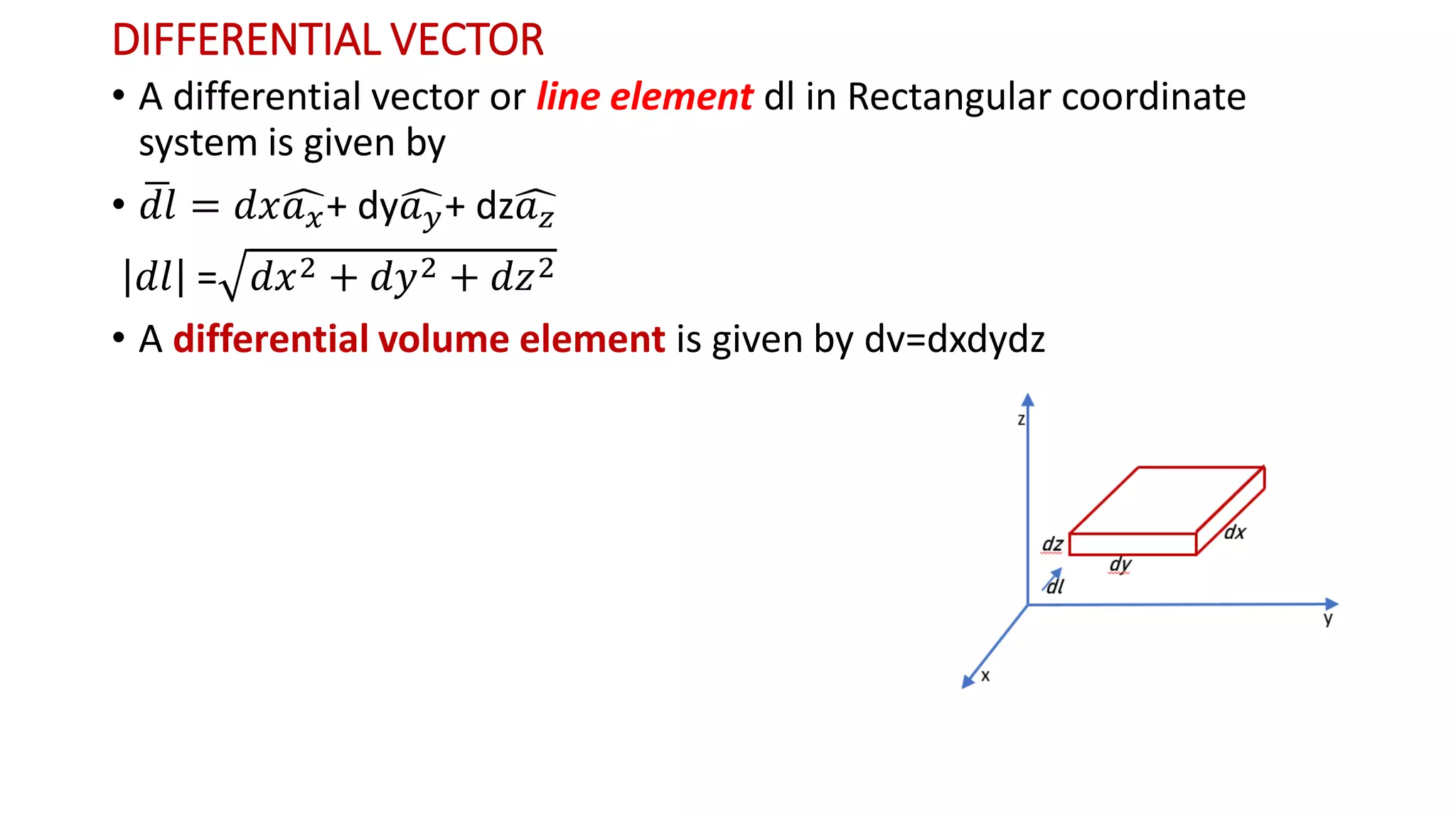
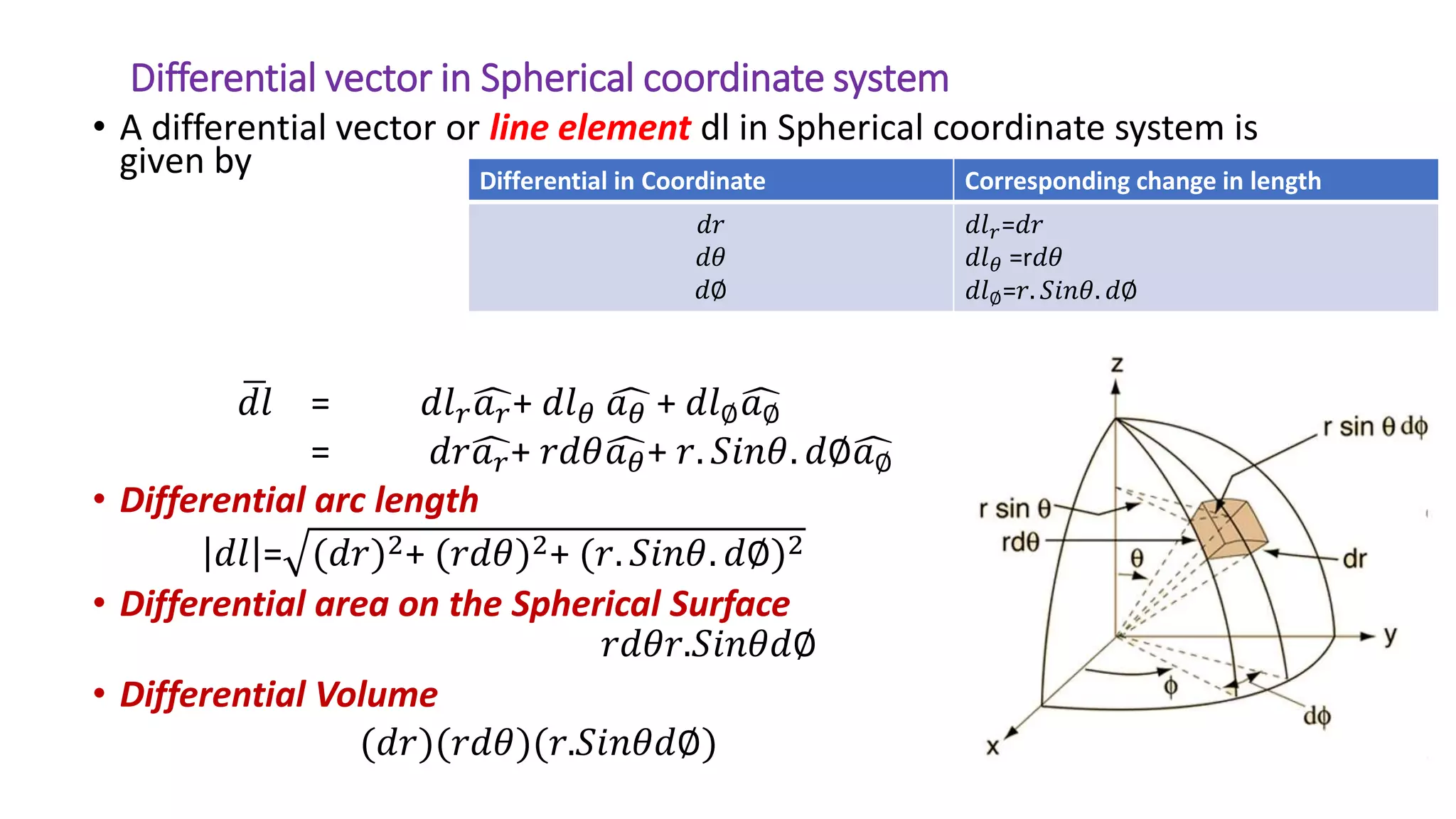
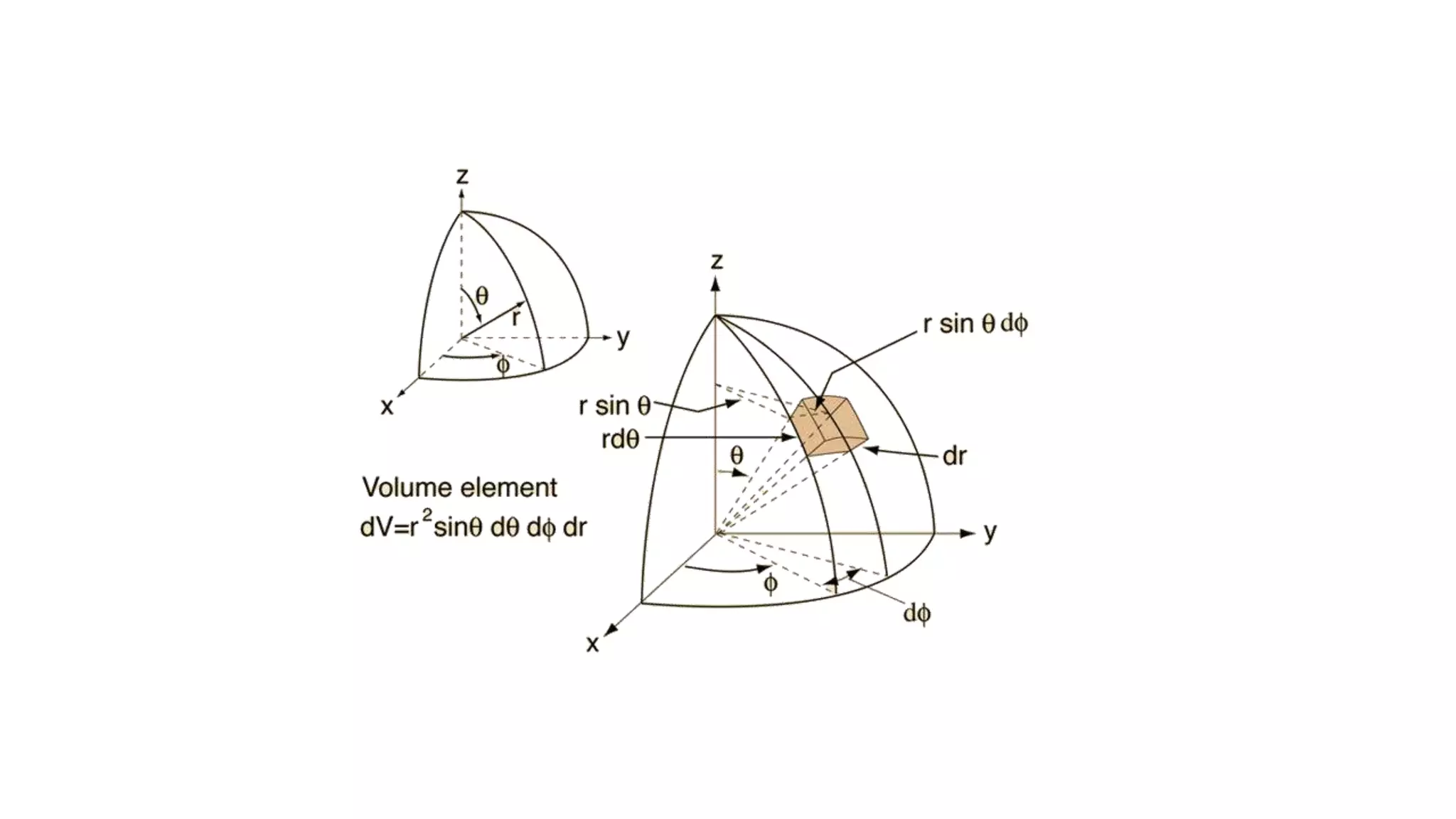
The document discusses various coordinate systems used in representing points in space, specifically orthogonal systems like Cartesian, cylindrical, and spherical coordinates. It details the relationships and transformations between these systems, including computation of position vectors, unit vectors, and differential elements in each system. Additionally, it provides mathematical relationships for converting between different coordinate systems and their respective transformation matrices.