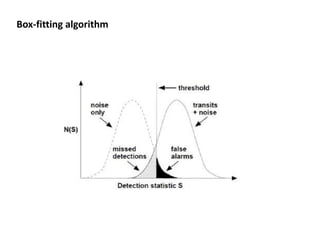
The box-fitting least squares (BLS) algorithm is used to detect periodic transits in light curves. It assumes the light curve only has two discrete values, fits box-shaped functions to folded light curves at different trial periods, and calculates the signal residue to identify the period with the maximum signal. The algorithm iterates over trial periods and transit durations to find the best-fitting five parameters that describe the period, depths, duration, and epoch of any transits present.

1. BLS (box-fitting least squares) algorithm
Paper:
A box-fitting algorithm in the search for periodic transits
G. Kovacs, S. Zucker and T. Mazeh, A&A 391, 369-377 (2002)
Box-fitting
Algorithm
@ridlo | 2016

2. Transit Method
Measure
Detect
Fig: Winn (2009)
Geometrical criterion Short transit duration < 5% P
White noise
Red noise
Algorithm: DFT (Discrete Fourier Transform) , PDM (Phase Dispersion
Minimization)?

3. Box-fitting algorithm
Assumptions
• The light curve only has two discrete values: high (H) and low (L). Ignoring gradual
ingress and egress phases of the transit.
• White noise embedded data set (Gaussian noise)
• Fitting to the box-shaped function to get five parameter P (period), H, L, q (fractional
transit length, ttransit = qP), and e (epoch of the transit).
• Only for detection (fast)

4. Box-fitting algorithm
Steps
1. Data centering
(pre processing)
Centered time series with
arithmetic average µ = 0

5. Box-fitting algorithm
Steps
2. Data folding binning
trial period
Folded with correct trial period and
binned
• Large deviation to the
correct period result in very
scattered folded time series
• Alleviates the problem of
missing data
Binning: less computation
Unbinned

6. Box-fitting algorithm
Steps
In every trial period P, the algorithm fits the different box-shaped functions to the
folded time series (applying the least squares method)
3. Fitting
With an assumption of a white noise embedded data set (Gaussian noise with
arithmetic average = 0), the algorithm apply the weighted least squares
data points with large variances
weight less

7. Box-fitting algorithm
Steps
For any test period ( ) in a trial period we minimize residual sum of squares
with

8. Box-fitting algorithm
Steps
Independent of test period
Define Signal Residue
We get a new expression for residual function
For a given trial period (P) we will get
the best fit from calculating this function
for any test period ( )
4. Do the iteration for different trial period (back to step 2)
Get the absolute maximum of SR
inner iteration
outer iteration

9. Box-fitting algorithm
Steps
Input x(t)
Data centering
Data folding
(with trial period (P))
Data binning
ITERATE over P
ITERATE over q ([qmin, qmax]) and over the data xi
Calculate SR for a test
period q ([i1, i2])
Save MAX(SR)
and corresponding
parameters

10. Box-fitting algorithm
Note
Every data point is assumed to have an uncorrelated Gaussian error. Larger value of
variance (σ) means smaller influence/weight (w). If the value of σ is assumed to be
constant then SR can be defined as
Implemented in
original code
n = number of data in L region
N = total number of data
Signal Detection Efficiency (SDE)
Author define this parameter,
in order to get significant detection, effective SNR should exceed 6
H - L

11. Box-fitting algorithm
Author’s original code (http://www.konkoly.hu/staff/kovacs/index.html)
http://www.konkoly.hu/staff/kovacs/bls_code.html
F77: bls.f, eebls.f
Python binding:
https://github.com/dfm/python-bls
https://github.com/hpparvi/PyBLS (modified: multithreaded, F2003)
Online: http://exoplanetarchive.ipac.caltech.edu/cgi-bin/TransitView/nph-
visibletbls?dataset=transits
Code
Exploration
http://nbviewer.jupyter.org/github/ridlo/exoplanet_notebook/blob/master/bls_
test01.ipynb
http://nbviewer.jupyter.org/github/ridlo/exoplanet_notebook/blob/master/bls_
test02.ipynb

12. Box-fitting algorithm
Result:

13. Box-fitting algorithm

14. References
A box-fitting algorithm in the search for periodic transits, G. Kovacs, S. Zucker and T.
Mazeh, A&A 391, 369-377 (2002)
J. Zijlstra's Bachelor Thesis