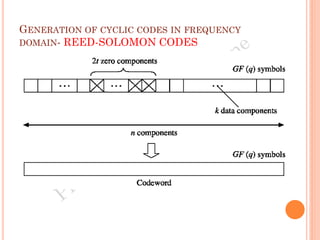
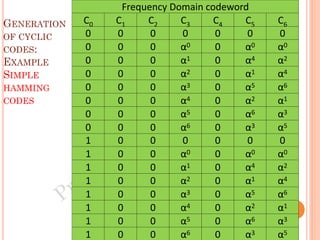
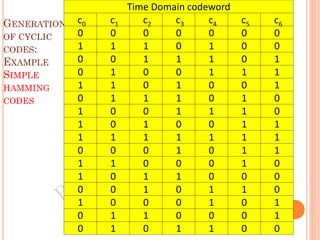
The document discusses the generation of error control codes, particularly BCH and Reed-Solomon codes, through Fourier transforms in Galois fields. It explains the relationship between discrete Fourier transforms in real and complex fields, and how similar principles apply in finite fields, emphasizing properties, theorems, and examples related to linear feedback shift registers and the significance of these codes in error correction. Key concepts include transformations, inverses, spectrum, and code generation with constraints on cyclic shifts and polynomial roots.

1. GENERATION OF ERROR CONTROL
CODES – BCH AND REED-
SOLOMON CODES IN FREQUENCY
DOMAIN
Fourier Transforms in Galois Field, Linear
complexity, LFSR, Conjugacy Constraints

2. FOURIER TRANSFORMS IN GALOIS FIELDS
 Discrete Fourier transforms reveal periodicities in input data
and the relative strengths of any periodic components.
 Discrete Fourier transform of a real sequence of numbers
will be a sequence of complex numbers of the same length.
 In complex field,
 Discrete Fourier transform of p = {pi, i=0,… N-1}, vector of
complex number, is a vector P = {Pk, k=0,…N-1}, given by
 where j = √(-1).
 The Fourier kernel exp(-j2πN-1
) is Nth root of unity in field
of complex numbers.
 In finite field GF(qm), element α of order n is an nth root of
unity.

3. FOURIER TRANSFORMS IN GALOIS FIELDS
 Drawing analogy between exp(-j2πN-1
) and α, Fourier
transform in Galois field can be given by—
 Let v = {vi, i=0,… n-1}, be a vector over GF(q), where n
divides qm-1 for some m, and let α be an element of GF(qm)
of order n.
 The Galois field Fourier transform of the vector v is the
vector V = {Vj, j=0,… n-1}, given by -
 Discrete index i is called time and v time domain function or
signal .
 Discrete index j is called frequency and V frequency
domain function or spectrum.

4. FOURIER TRANSFORMS IN GALOIS FIELDS
 In DFT, though function p is real, transform P is complex.
 Similarly in GFFT, though time domain function v is over
GF(q), the spectrum V is over GF(qm).
 In DFT, exp(-j2πN-1
) exists for all values of n.
 In Galois fields, α exists only if n divides qm-1.
 To ensure v over GF(q) and V over GF(qm), n = qm-1.
 Inverse Fourier transform :

5. EXAMPLE
 Let 1011000 be a vector over GF(2), and n = 23-1 for m=3,
and let α be an element of GF(23) of order 7.Find its FT in
Galois field GF(23).
 Solution: Vj = ∑ α
ij
vi , i = 0…n-1
 V0 = ∑ αo i
vi = 1+1+1 = 1
 V1 = ∑ αi
vi = 1+1. α2
+ 1. α3
= α4
.
 V2 = ∑ α
2i
vi = 1+1. α
4
+ 1. α
6
= α .
 V3 = ∑ α3i
vi = 1+1. α6
+ 1. α9
= 0 .
 V4 = ∑ α4i
vi = 1+1. α8
+ 1. α12
= α2
.
 V5 = ∑ α
5i
vi = 1+1. α
10
+ 1. α
15
= 0 .
 V6= ∑ α6i
vi = 1+1. α12
+ 1. α18
= 0 .
 V = 1 α4
α 0 α2
0 0 .
 Confirm by finding inverse Fourier transform.

6. EXAMPLE
 Confirm by finding inverse Fourier transform.
 Solution: vi = (1/n)∑ α-ij
Vj , j = 0…n-1
 v0 = (1/7) ∑ Vj = (1+ α4
+ α + α2
)/7 = 1 mod-7
 v1 = (1/7) ∑ α-j
Vj = (1+ α4
α-1
+ α α-2
+ α2
α-4
)/7
 = (1+ α4
α6
+ α α5
+ α2
α3
)/7 = 0
 v2 = (1/7) ∑ α-2j
Vj = (1+ α4
α-2
+ α α-4
+ α2
α-8
)/7 = 1
 v3 = (1/n) ∑ α-3j
Vj = (1+ α4
α-3
+ α α-6
+ α2
α-12
)/7 = 1
 v4 = (1/n) ∑ α-4j
Vj = (1+ α4
α-4
+ α α-8
+ α2
α-16
)/7 = 0
 v5 = (1/n) ∑ α-5j
Vj = (1+ α4
α-5
+ α α-10
+ α2
α-20
)/7 = 0
 v6 = (1/n) ∑ α-6j
Vj = (1+ α4
α-6
+ α α-12
+ α2
α-24
)/7 = 0
 v = 1011000

7. FOURIER TRANSFORMS IN GALOIS FIELDS-
PROPERTIES
 If vi ↔ Vj then--
 v + v’ ↔ V + V’ Additivity
 αil
vi ↔ V((j+l)) Modulation
 v((i-l)) ↔ αjl
Vj Translation
 Proof
 Modulation ∑ αij
(αil
vi ) = ∑ αi(j+l)
vi = V((j+l))
 OR (1/n)∑ α
-ij
V ((j+l)) j+l=k or j=k-l
 (1/n)∑ α-i(k-l)
Vk = (1/n)∑ α-ik
αil
V ((j+l)) = αil
(1/n)∑ α-ik
V ((j+l)) =
 = αil
vi
 Translation (1/n)∑ α-ij
αjl
Vj= (1/n)∑ α-(i-l)j
Vj = v((i-l))
 OR ∑ αij
v((i-l)) i-l=k or i=k+l
 ∑ α
(k+l)j
vk= ∑ α
jl
α
kj
vk = α
jl
∑ α
kj
vk = α
jl
Vj
 = αil
vi

8. FOURIER TRANSFORMS IN GALOIS FIELDS-
PROPERTIES
 If Ej = FjGj then ei =∑n-1
l=0
f((i-l)) gl. Convolution
 If ei = fi gi then Ej =(1/n)∑n-1
k=0
F((j-k)) Gk.

9. CONVOLUTION
 Let ei = figi i=0,… n-1.
 Then Fourier transform Ej, where double parenthesis
denotes modulo-n arithmetic on the indices, is given as-
Proof: Taking FT of ei = figi

10. FOURIER TRANSFORMS IN GALOIS FIELDS -
THEOREMS
 The polynomial v(x) has a zero (root) at αj
iff the jth
frequency component Vj equals zero.
 The polynomial V(x) has a zero (root) at α-i
iff the ith
time
component vi equals zero. where
 v(x) = vn-1xn-1
+…+ v1x + v0
 V(x) = Vn-1x
n-1
+…+ V1x + V0
 Proof:
 v(αj
) = ∑viαij
= Vj = 0 From FT formula
 Same for other statement.
 Code can be generated in time domain as well as frequency
domain.

11. EXAMPLE
 Example v = 1011000 V = 1 α
4
α 0 α
2
0 0.
 v(x) = 1+x
2
+x
3
. V(x) = 1+α
4
x+αx
2
+ α
2
x
4
.
 V3, V5, and V6 = 0
 Check if α
3
, α
5
, and α
6
are roots of v(x) and other elements are
not.
 v(α
3
) = 1+ α
6
+ α
9
= 0 .
 v(α
5
) = 1+ α
10
+ α
15
= 0 .
 v(α
6
) = 1+ α
12
+ α
18
= 0 .
 Similarly--
 v1, v4, v5, and v6 = 0
 Check if α
-1
, α
-4
, α
-5
, and α
-6
are roots of V(x) and other elements
are not.
 V(α
-1
) = 1+ α
4
α
-1
+ α α
-2
+ α
2
α
-4
= 0 .
 V(α
-4
) = 1+ α
4
α
-4
+ α α
-8
+ α
2
α
-16
= 0
 V(α
-5
) = 1+ α
4
α
-5
+ α α
-10
+ α
2
α
-20
= 0
 V(α
-6
) = 1+ α
4
α
-6
+ α α
-12
+ α
2
α
-24
)/7 = 0
 Proved

12. EXAMPLE
 Consider vector v of block length n and weight 1 with vm as
single non-zero component.
 Vj =∑n-1
i=0
αij
vi = αjm
vm j=1,…n-1.
 Vj = vm+ αm
vm+ α2m
vm+… α(n-1)m
vm.
 Above spectrum V can be generated by Recursion
(generating future values using past values of any length).
 By multiplying α
m
to previous one value starting from v0=vm.
 Spectrum of a vector of weight 1 can be generated by a
linear recursion of length 1.
 Special case of linear complexity.

13. IMPORTANCE OF REED-SOLOMON CODES
 RS codes are important for several reasons:
 (i) They are the natural codes to use when a code is
required of length less than the size of the field. For, being
MDS, they have the highest possible minimum distance.
 (ii) They are convenient for building other codes, as they
can be mapped into binary codes with high minimum
distance.
 (iii) They are also used in constructing concatenated and
Justesen codes.
 (iii) They are useful for correcting bursts of errors.

14. LINEAR COMPLEXITY LA
 La = Degree of its minimum polynomial m
 = Length of shortest Linear Feedback Shift Register (LFSR)
capable of producing a sequence which agrees with ‘a’ for
first k entries a0…ak-1.
 = maximum number of linearly independent vectors among
state vectors produced by LFSR.
 La = n-k = d-1

15. LINEAR FEEDBACK SHIFT REGISTER (LFSR)
 Machine consisting of registers R0 ..Rm-1, arranged in a row
with X-OR gates.
 Feedback connections provided from Rm-1 to shift registers
through X-OR based on constant Ci , 1≤i ≤m, being 0 or 1.
 c(x) = 1+c1x+c2x2
+…. cm-1xm-1
.
 Example: LFSR of length 10.
 c(x) = 1+x+x3
+x4
+x7
+x10
.
 Initial state s0…s9 =1001001
 Generatesμ 100 100 …
+
1 0 0 1 0 0 1 0 0 1
+++

16. LINEAR FEEDBACK SHIFT REGISTER (LFSR)
 Any sequence generated by LFSR of length L with
feedback polynomial C is also generated by LFSR
whose feedback polynomial is a multiple of C.
 A sequence generated by LFSR of length L with
feedback polynomial C may also be generated by
‘shorter’ LFSR with feedback polynomial C’ iff C is not
irreducible over GF(q).
 c(x) = 1+x+x3
+x4
+x7
+x10
= (1+x+x7
)(1+x3
)
 Hence same sequence will be generated by (1+x3
).
 Hence linear complexity = 3
0 0 1

17. LINEAR COMPLEXITY - THEOREMS
 Linear complexity of a finite length vector V, cyclically
repeated, is equal to hamming weight to its inverse FT v.
 Hamming weight of a vector V is equal to the linear
complexity of its inverse FT v.
 Example: v = 1011000 V = 1 α4
α 0 α2
0 0.
 La of V = 3
 La of v = 4

18. SPECTRAL PROPERTIES OF CYCLIC CODES –
REED-SOLOMON CODES
 A R-S code C of block length n over GF(q), with n a divisor
of q-1, is defined as the set of all codewords whose FT is
equal to zeros in a specified block of d-1 consecutive
components j0, j0+1,… j0+d - 2 .
 As n divides q-1, codewords and spectrum components are
symbols in same field GF(q).
 If codeword C is cyclically shifted by one place, then its
spectral component cj is multiplied by αj
.
 If cj = zero, cjαj
= zero, cyclic shift of C does not alter
spectrum and hence a valid codeword.
 Coded using g(x)= (x- α j0) (x- α j0+1
) (x- α j0+2
) …(x- α j0+d-2
)
 dmin = d2t+1
 Polynomial of degree n-k = d-1

19. FREQUENCY /TRANSFORM DOMAIN ENCODER
 Every spectrum consistent with the spectral constraints
yields a code word.
 (d-1) cyclically consecutive frequencies j= j0, j0+1,… j0+d - 2
chosen as set of spectral components constrained to be
zero.
 (n-(d-1)) unconstrained components filled with data symbols
from GF(q).
 Inverse FT produces non-systematic codewords.
 d=2t+1, (n,n-d+1) codeword.
 Roots of g(x) = roots of c(x)
 If αi
is root of c(x), Vi = 0.
 d-1=n-k roots, and d-1 components zero.

20. EXAMPLE
 (7,5) cyclic code over GF(8) with t=1, j0= 1, (common choice)
 g(x)= (x- α) (x- α2
) (x- α3
) …(x- α2t
) d=2t+1
 g(x)= (x- α) (x- α2
) = x2
+ α4
x + α3
.
 Let data d(x) = α4
x4
+ x3
+ α3
x2
+ αx +α6
.
 c(x) = d(x)g(x)=α4
x6
+ α3
x5
+ α2
x4
+ 0.x3
+ α5
x2
+ α6
x +α2
.
 (7,3) RS code over GF(8) with t=2, j0= 4,
 g(x)= x4
+ α6
x3
+ α6
x2
+ α3
x +α.
 Let data d(x) = α4
x2
+ x +α3
.
 c(x) = α4
x6
+ αx5
+ α6
x4
+ 0.x3
+ 0.x2
+ α5
x +α4
.
 (15,11) RS code over GF(16) with t=2, j0= 1,
 d(x) = x4
+ α13
x3
+ α6
x2
+ α3
x + α10
.
 c(x) = ?

21. CONJUGACY CONSTRAINT
 Any vector in GF(q) gives FT in GF(qm)
 But any vector in GF(qm) does NOT always give Ŧ-1 in
GF(q).
 As in complex field, Ŧ-1(real) = real iff V(-f) = V(f).
 Conjugacy Constraint Theorem: Let V be a vector of
length n of elements of GF(qm) where n is a divisor of qm-1.
Then the inverse Fourier transform v is a vector of length n
of elements of GF(q) if and only if following is satisfied:-
 Vj
q
= V((qj)) j=0,…n-1.
 Proof: In GF, (a+b)pr
= apr
+bpr
for any integer r.
 If vi is an element of GF(q), then vi
q
= vi. Hence..
 Vj
q
= (∑ αij
vi )
q
= (∑ α
qij
vi
q
) = (∑ α
qij
vi) = V((qj))

22. CONJUGACY CLASSES
 To apply Conjugacy theorem, the integers modulo-n are
divided into a collection of sets known as Conjugacy classes
as—
 Aj = { j, jq, jq2, …jqmj-1}
 where m is smallest positive integer satisfying jqmj =j
modulo n. Example: q=2, n=7, ..
 A0 = {0}
 A1 = {1,2,4}
 A2 = {2,4,1} A1 = A2
 A3 = {3,6,5} Test each set on previous example.
 Conjugacy class Aj specifies a set of frequencies in the
spectrum called a Chord.
 If the time domain signal is in GF(q), then the value of the
spectrum at any frequency in a conjugate class specifies the
value of the spectrum at all other frequencies in that class.
 Find conjugate classes for modulo-15, 21, 31.

23. Q-ARY TRACE
 The q-ary trace of an element β of GF(qm) is the sum-
 trace(β)= ∑m-1
i=0
βqi
= β+βq
+ βq2
+…+ βqm-1
.
 Q-ary trace is an element of GF(q).
 Example: if q=2, m=3, GF(23)
 trace(β)= (β+β2
+ β22
)
 (trace(β))q
= (∑βqi
)q
= ∑ βqi+1
= βq
+ βq2
+…+ βqm-1
+βqm
 = trace(β) βqm
= β
 If β has m elements in its Conjugacy class, then trace(β) is
sum of all elements in class.
 If β has r elements in its Conjugacy class, r divides m, then
each element added into trace m/r times.
 Check above with modulo-15 chord.

24. GENERATION OF CYCLIC CODES IN FREQUENCY DOMAIN
 Non-systematic cyclic code c(x) = g(x)d(x).
 This is cyclic convolution in time domain as-
 Ci =∑n-1
k=0
g((i-k)) dk.
 In frequency domain Cj = GjDj.
 Any spectrum satisfying above is frequency-domain
codeword over GF(qm) provided all components in time
domain are GF(q)-valued.
 Given a set of spectral components j1,…jn-k called parity
frequencies, the cyclic code C is the set of words over GF(q)
whose spectrum is constrained to zero in consecutive
components j1,…jn-k.
 Only few of spectra designed as above give codeword in
GF(q) if they satisfy Conjugacy constraint theorem.

25. GENERATION OF CYCLIC CODES IN FREQUENCY DOMAIN-
REED-SOLOMON CODES
 n= q-1 or a factor.
 Set of 2t consecutive frequencies of the spectrum are
chosen symbols, to be constrained to zero. 2t = d-1 = n-k
 The n-2t unconstrained components of spectrum are filled
with information symbols from GF(q).
 Inverse FT then produces nonsystematic (n,n-2t) codeword.

26. GENERATION OF CYCLIC CODES IN FREQUENCY
DOMAIN- REED-SOLOMON CODES

27. GENERATION OF CYCLIC CODES: EXAMPLE
SIMPLE HAMMING CODES
 Encode SEC (7,4) hamming(Cyclic) code in frequency
domain in GF(23).
 Components C1 and C2 are chosen as parity frequencies to
correct single error. t=1
 k=4, 16 combinations. Hence information is contained in
two information frequency components C0 and C3.
 Using Conjugacy constrain theorem, obligatory frequency-
 C1
4
= C2
2
= C4 = 0
 C3
4
= C6
2
= C5 = 0
 C0
2
= C0. Hence C0 can be either 0 or 1.
 Hence equivalent bit content of C0 is one bit.
 Equivalent bit content of C3 is three bits. GF(23).
 Hence 4 information bits uniquely specify the spectrum.
 Find 16 codewords after inverse FT.

28. GENERATION
OF CYCLIC
CODES:
EXAMPLE
SIMPLE
HAMMING
CODES
Frequency Domain codeword
C0 C1 C2 C3 C4 C5 C6
0 0 0 0 0 0 0
0 0 0 α0 0 α0 α0
0 0 0 α1 0 α4 α2
0 0 0 α2 0 α1 α4
0 0 0 α3 0 α5 α6
0 0 0 α4 0 α2 α1
0 0 0 α5 0 α6 α3
0 0 0 α6 0 α3 α5
1 0 0 0 0 0 0
1 0 0 α0 0 α0 α0
1 0 0 α1 0 α4 α2
1 0 0 α2 0 α1 α4
1 0 0 α3 0 α5 α6
1 0 0 α4 0 α2 α1
1 0 0 α5 0 α6 α3
1 0 0 α6 0 α3 α5

29. GENERATION
OF CYCLIC
CODES:
EXAMPLE
SIMPLE
HAMMING
CODES
Time Domain codeword
c0 c1 c2 c3 c4 c5 c6
0 0 0 0 0 0 0
1 1 1 0 1 0 0
0 0 1 1 1 0 1
0 1 0 0 1 1 1
1 1 0 1 0 0 1
0 1 1 1 0 1 0
1 0 0 1 1 1 0
1 0 1 0 0 1 1
1 1 1 1 1 1 1
0 0 0 1 0 1 1
1 1 0 0 0 1 0
1 0 1 1 0 0 0
0 0 1 0 1 1 0
1 0 0 0 1 0 1
0 1 1 0 0 0 1
0 1 0 1 1 0 0

30. GENERATION OF CYCLIC CODES: BCH CODES
 Example: Design TEC BCH code over GF(64). t=3
 Choosing C1, C2, C3, C4, C5, and C6 to be parity frequencies and
constrained to be zero. (2t symbols)
 Then C0, C7, C9, C11, C13, C15, C21, C23, C27 andC31 are
information symbols. Check for validity. How?
 Find smallest n for which Cj
n
= Cjn mod-63 = Cj (for n=64,32, 16,
8, 4, 2). Always mod-63 as GF(64).
 C31 –
 n=64– (C31)
64
= C((1984)) = C31
 n=32 -- (C31)
32
= C((992)) ≠ C31
 n=16 -- (C31)
16
= C((496)) ≠ C31
 n=8 -- (C31)
8
= C((248)) ≠ C31
 n=4 -- (C31)
4
= C((124)) ≠ C31
 n=2 -- (C31)
2
= C62 ≠ C31
 Hence for C31 n=64. 64 symbols possible for position C31.
 Needs 6 bits to encode in time domain. GF(2
6
).

31. GENERATION OF CYCLIC CODES: BCH CODES
 C27 –
 n=64– (C27)64
= C((1728)) = C27 mod-63
 n=32 -- (C27)32
≠ C27 ,
 n=16 -- (C27)16
≠ C27
 n=8 -- (C27)8
= C((216)) = C27
 n=4 -- (C27)4
= C((108)) ≠ C27
 n=2 -- (C27)2
= C54 ≠ C27
 Hence for C27 n=8. Needs 3 bits to encode. GF(23
).
 8 symbols possible for position C27.
 Needs 3 bits to encode in time domain. GF(23
).

32. GENERATION OF CYCLIC CODES: BCH CODES
 Similarly C23, C15, C13, C11, C7, n=64. Each position can
have any of 64 symbols.
 Needs 6 bits to encode each in time domain. GF(26
).
 For C21 n=4. Needs 2 bits to encode. GF(22
). Solve
 For C9 n=8. Needs 3 bits to encode. GF(23
).
 For C0 n=2. Needs 1 bit to encode. GF(2 ).
 Hence total information symbols are --
 2.64.8.64.64.64.4.64.8.64 = 35184372088832 = 245
 Hence total 45 information bits to specify these symbols in
time domain. Data = 245
 Gives TEC (63,45) BCH code.
 Remaining symbols (63-16=46)?

33. GENERATION OF CYCLIC CODES: BCH CODES
 Remaining symbols (63-16=46)?
 Remaining symbols are called obligatory symbols and are
obtained by property of Conjugacy.

34. GENERATION OF CYCLIC CODES: BCH CODES
 Complete spectrum of 64 symbols are transformed into time
domain 245 codewords.
 Operation of decoder is same as earlier irrespective of
time/frequency domain encoding.
 At last step, to extract information, however, decoder must
know how information is stored in codeword.
 If information bits are encoded in the frequency domain,
they must be read out from frequency domain.