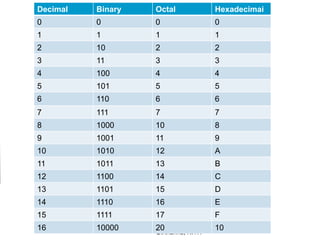
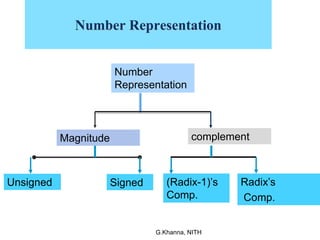
1. The document discusses different number representation systems like binary, octal, hexadecimal and their conversions to decimal numbers. 2. It explains various methods for representing signed numbers like signed magnitude representation, 1's complement and 2's complement methods. The 2's complement method allows representing numbers in the range of -(2n-1) to +(2n-1-1). 3. Binary addition and subtraction algorithms are covered along with examples. Radix complement method is discussed for subtraction which involves converting the number to its radix-1's complement before addition.

1. NUMBER SYSTEM
Binary Arithmetic
Dr. (Mrs.) Gargi Khanna
Associate Professor
Electronics & Communication Engg. Deptt..
National Institute of Technology Hamirpur (HP)
Chapter-I
Lecture-III

2. G.Khanna, NITH
Decimal Binary Octal Hexadecimai
0 0 0 0
1 1 1 1
2 10 2 2
3 11 3 3
4 100 4 4
5 101 5 5
6 110 6 6
7 111 7 7
8 1000 10 8
9 1001 11 9
10 1010 12 A
11 1011 13 B
12 1100 14 C
13 1101 15 D
14 1110 16 E
15 1111 17 F
16 10000 20 10

3. Number Representation
Number
Representation
Signed
complementMagnitude
Unsigned Radix’s
Comp.
(Radix-1)’s
Comp.
G.Khanna, NITH

4. Unsigned Representation
All bits are used to represent the magnitude.
+7 = 111
-7 = Can’t be represented
1111= 15
1000=8
Range 0 to (2n-1)
G.Khanna, NITH

5. Signed Representation
MSB is reserved for sign
MSB =1 Negative number
MSB= 0 Positive number
+6 = 0110
-6 = 1110
+13 = 01101
-13 = 11101
Range => -(2n-1-1) to +(2n-1-1)
Where, n= no. of variables
n=4 has range -7 to +7
G.Khanna, NITH

6. Radix and (Radix-1)’s
Complement
r’s Complement (r-1)’s Complement
r=10 10’s Comp. 9’s Comp.
r=2 2’s Comp. 1’s Comp.
r=8 8’s Comp. 7’s Comp.
r=16 16’s Comp. 15’s Comp.
G.Khanna, NITH

7. 1’s Complement
1’s complement obtained by subtracting each bit by 1
+6 = 0110
-6 = 1001
+9 = 01001
-9 = 00110
+0 = 0000 (+ve zero)
-0 = 1111 (-ve zero)
Range => -(2n-1-1) to +(2n-1-1)
G.Khanna, NITH

8. Radix-1 Complement Method
Subtract each symbol by base-1
 Decimal Number, subtract each digit by 9
Example (-147)10=852
 Octal Number subtract each digit by 7
Example (-123)8=654
 Hexadecimal number subtract each digit
by 15
Example (-6A1)16=95E
Diminished RadixG.Khanna, NITH

9. 2’s Complement
Take 1’s complement and add 1 ,
+4 = 0100
it’s 1’s Complement = 1011
it’s 2’s Complement = 1100 = -4
Range => -(2n-1) to +(2n-1-1)
G.Khanna, NITH

10. Radix’s Complement Method
 Subtract each symbol by base-1 and add 1
 Decimal Number, subtract each digit by 9 and add 1
Example -147=852+1=853
 Octal Number subtract each digit by 7 and add1
Example -123=654+1=655
 Hexadecimal number subtract each digit by 15 and
add 1
Example -6A1=95E+1=95F
G.Khanna, NITH

11. Double Precision Number
 16 bit computer having 16 Bit word length can
represent numbers in range 32767 to -32768
 To represent greater number two storage
location used –Double Precision
 MSB for sign and remaining 31 bits for
number
 Triple precision
G.Khanna, NITH

12. Binary Addition
4 Possible Binary Addition Combinations:
(1) 0 (2) 0
+0 +1
00 01
(3) 1 (4) 1
+0 +1
01 10
SumCarry
G.Khanna, NITH

13. Binary Addition
G.Khanna, NITH
19+62

14. Addition
 Add two digits
 (456)10
+(157)10
(6 1 3)10
 (446)8
+(156)8
(6 2 4)10
G.Khanna, NITH

15. Subtraction Using Radix-1’s
Complement Method
 Convert no. to be subtracted to it’s radix-1’s
complement form.
 Perform the addition.
 If the final carry is 1, then add to the result obtained
in step 2.
 If the final carry is zero, result obtained in step 2 is
negative and is in the radix-1’s complement form.
G.Khanna, NITH

16. Binary Subtraction Using Radix’s
Complement Method
 Find Radix’s complement of the number to be
subtracted.
 Perform the addition.
 If the final carry is generated, then the result is
positive and in its true form.
 If final carry is not produced, then the result is
negative and in its Radix’s complement form.
G.Khanna, NITH

17. G.Khanna, NITH
1. First, we need to convert 00112 to its negative
equivalent in 1's complement.
0111 (7)
- 0011 - (3)
2. To do this we change all the 1's to 0's and 0's to
1's. Notice that the most-significant digit is now 1
since the number is negative.
0011 -> 1100
3. Next, we add the negative value we computed to
01112. This gives us a result of 101012.
0111 (7)
+1100 +(-3)
10011 (?)
4. Notice that our addition caused an overflow bit. we
add this bit to our sum to get the correct answer. If
there is no overflow bit, then we leave the sum as
it is.
0011
+ 1
0100 (4)
5. This gives us a final answer of 01002 (or 410).
0111 (7)
- 0001 - (3)
0100 (4)
Subtraction with One's Complement method
Subtracting 310 from 710 using 1's complement.

18. G.Khanna, NITH
Decimal
Addition
Binary
representation
2's Complement
Addition
+100 0110 0100 01100100
- 30 0001 1110 11100010
+70 1 0100 0110
Subtraction with Two's Complement method
Discard the carry
and answer is
positive
Decimal Addition Binary representation
2's Complement
Addition
+30 00011110 00011110
- 100 01100100 10011100
-70 10111010
No carry and
answer is
negative, in 2’s
complement form
and magnitude
is 01000110

19. G.Khanna, NITH