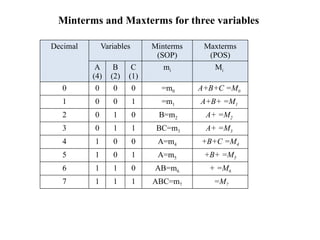
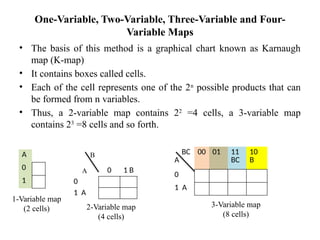
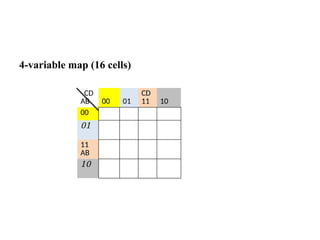
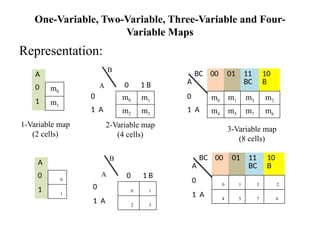
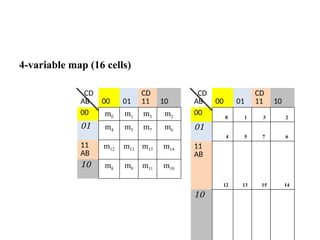
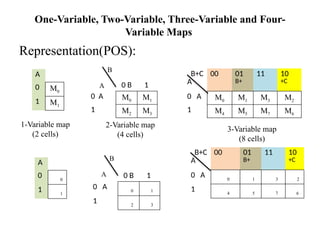
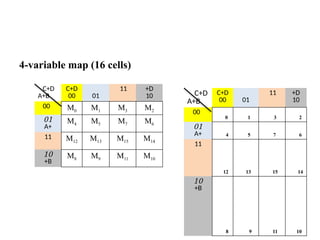
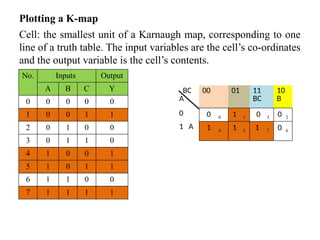
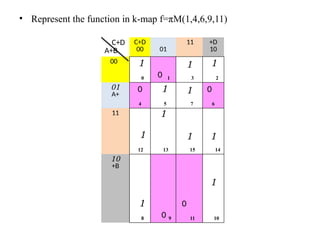
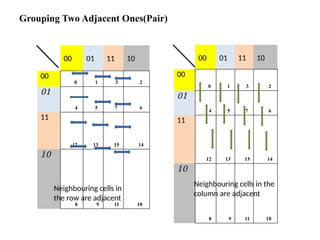
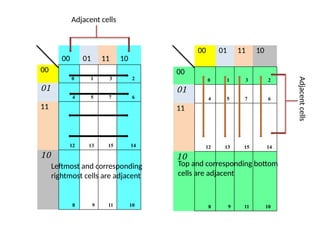
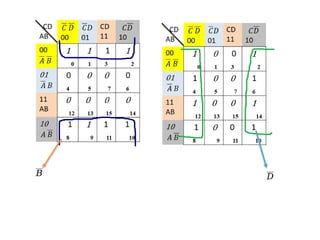
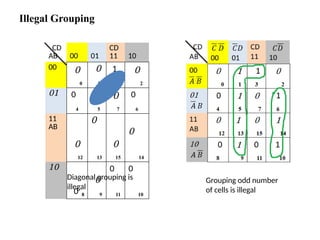
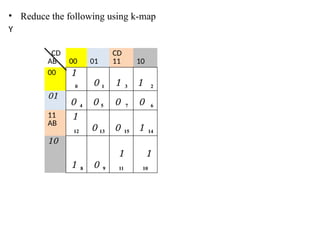
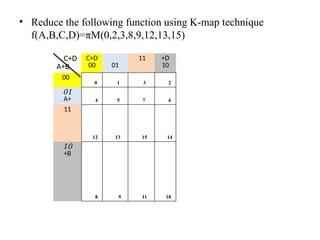
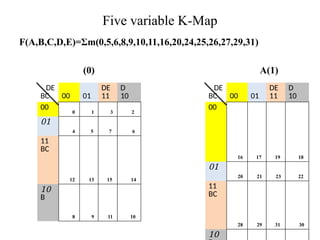
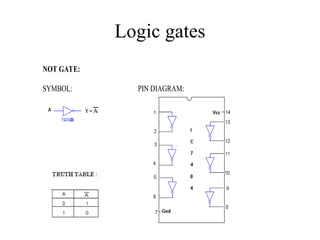
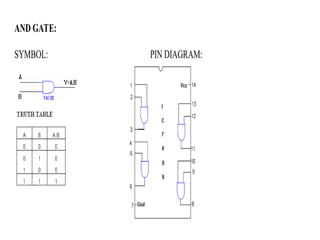
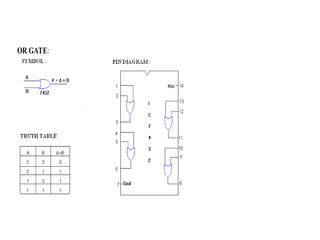
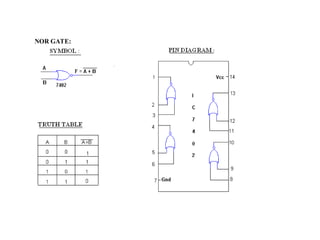
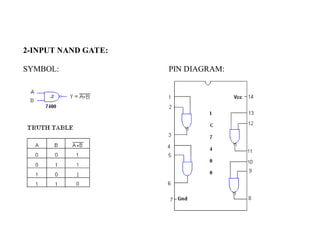
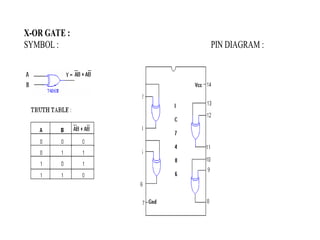
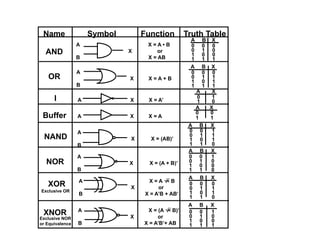
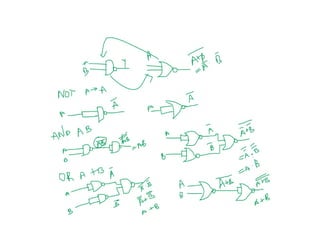
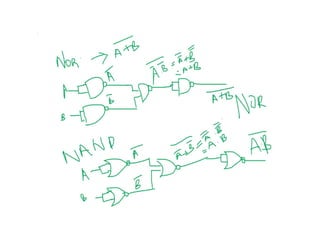
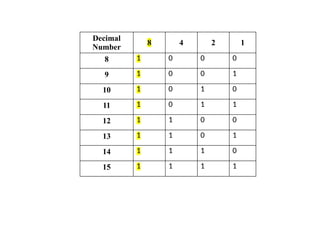
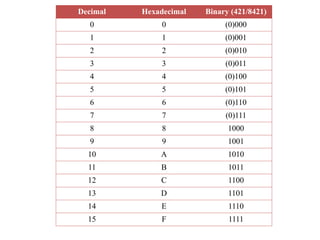
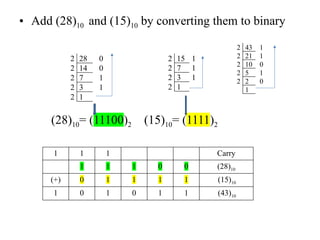
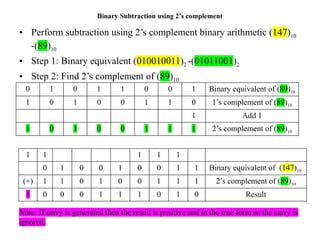
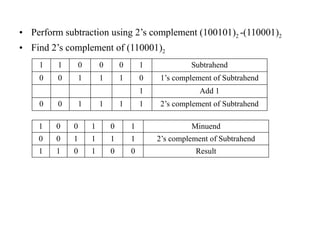
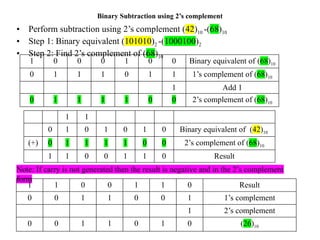
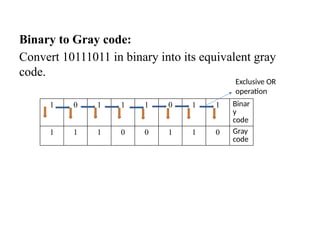
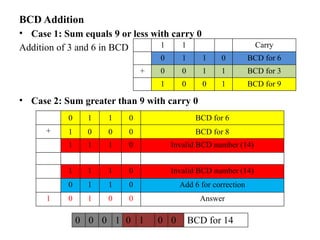
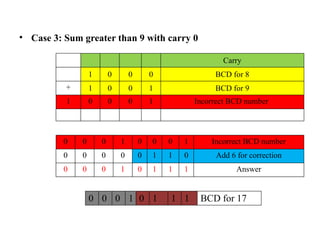
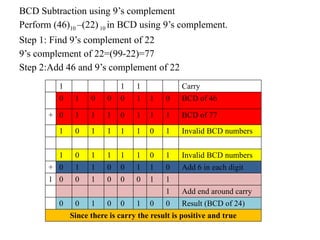
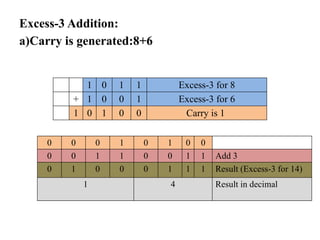
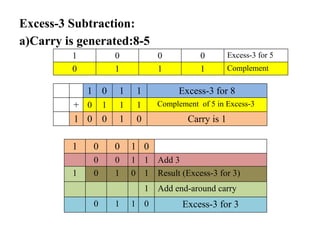
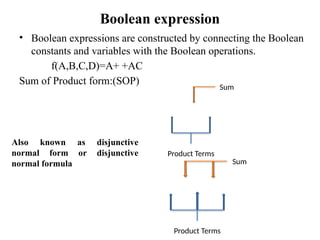
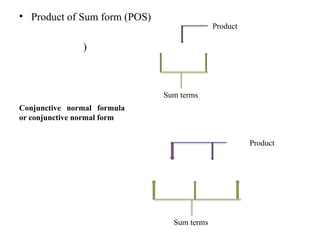
Digital Electronics,Number Systems Decimal, Binary, Octal, Hexadecimal, radix conversion ,1's and 2's complements, Codes – Binary, BCD, Excess 3, Gray, Alphanumeric codes, Boolean theorems and Postulates, Logic gates ,Universal gates ,Sum of products and product of sums , Minterms and Maxterms, Karnaugh Map Minimization.








































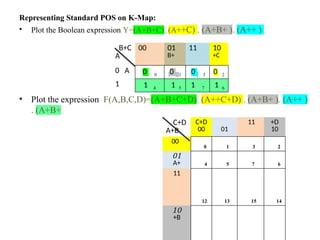
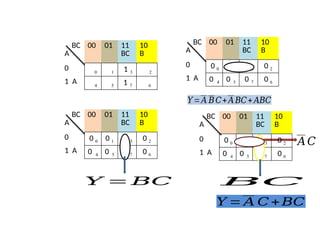
![Step 2: OR sum term with (missing literal . its complement)
Y=[A+(B. )+ (C. ) ]. (A+B+C)
Step 3: Expand the terms and reorder literals
Y=(A+B). (A+)+ (C. ) ]. (A+B+C)
Y=(A+B+C). (A++C) . (A+B+ ). (A++ ). (A+B+C)
Step 4: Omit repeated sum terms
Y=(A+B+C). (A++C) . (A+B+ ). (A++ ). (A+B+C)
Y=(A+B+C). (A++C) . (A+B+ ). (A++ )](https://image.slidesharecdn.com/de-unit-i-250527094925-95441392/85/Digital-Electronics-UNIT-I-DIGITAL-FUNDAMENTALS-63-320.jpg)