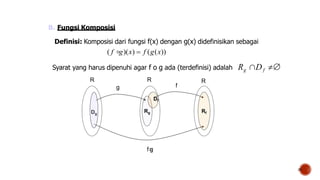
Dokumen ini membahas tentang fungsi matematis, termasuk definisi, notasi, dan contoh fungsi serta grafiknya. Penjelasan mencakup konsep variabel bebas dan tak bebas, domain, range, serta jenis fungsi seperti fungsi linear dan kuadrat. Terdapat juga penjelasan mengenai fungsi periodik, komposisi fungsi, serta sifat-sifat fungsi ganjil dan genap.


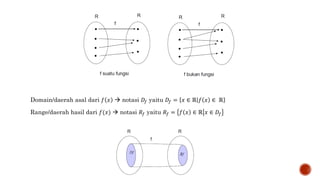










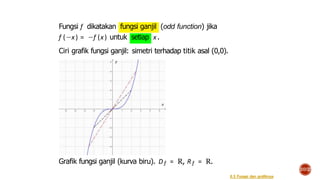
![Fungsi f dikatakan fungsi genap (even function) jika
f (x) = f (−x) untuk setiap x.
Ciri grafik fungsi genap: simetri terhadap sumbu y.
Grafik fungsi genap (kurva biru). Df = R, Rf = (−∞, 5].
Kalkulus 1 (SCMA601002) 19/23
0.5 Fungsi dan grafiknya](https://image.slidesharecdn.com/fungsi-240207010403-4831a464/85/fungsi-pptx-19-320.jpg)




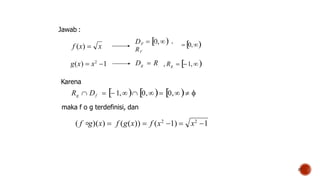
![
x R | x2
1 0 x R | (x 1)(x 1) 0
(,1] [1,).
x D | g(x) D
x R | x2
g f
D f ∘g
1 0,
f
R
y R | y f (t) , t R
f ∘
g g
t , t 1
[0,).
28
y 0 | y ](https://image.slidesharecdn.com/fungsi-240207010403-4831a464/85/fungsi-pptx-28-320.jpg)
