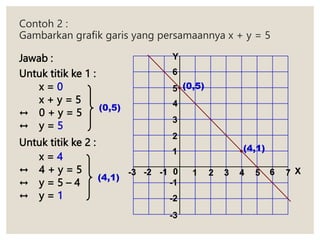
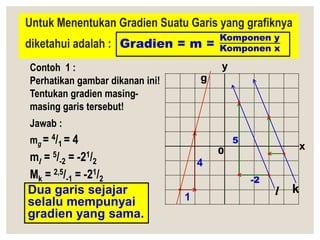
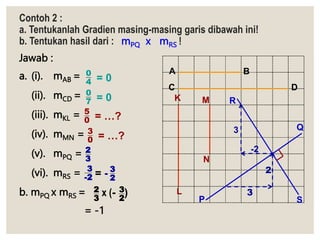
Dokumen ini membahas tentang persamaan garis lurus, termasuk pengertian, bentuk, grafik, dan metode untuk menentukan gradiennya. Selain itu, dijelaskan juga mengenai persamaan yang ekivalen dan cara menggambar grafik serta menentukan persamaan garis dengan informasi titik dan gradien. Contoh-contoh diberikan untuk memperjelas konsep dan aplikasi dari teori yang disampaikan.

1. BAB 4
PERSAMAAN GARIS LURUS

2. A. PENGERTIAN PERSAMAAN GARIS LURUS
◦ Pada f(x) = ax + c , dapat dirobah penulisannya
menjadi y = ax + c.
◦ y = ax + c disebut Persamaan garis lurus Dua
Variabel atau Persamaan Linier Dua Variabel.
◦ Bentuk Persamaan Garis Lurus ada beberapa jenis ,
misalnya :
1. by = ax + c
2. ax + by = c
3. ax + by + c = 0
4. ax = c
5. by = c

3. GRAFIK PERSAMAAN GARIS LURUS
Soal pengantar :
Harga :
3 pensil + 2 buku = Rp 4.800
Dari pernyataan diatas :
(i). Seandainya pensil gratis
berapakah harga 1 buku?
(ii). Andaikan buku yang gratis
berapa harga 1 pensil?
Catatan :
Gratis berarti harganya Rp 0,-
Tentukan harga satu buku pada
masing-masing titik yang hitam
pada grafik dikanan ini! 0 400
800
1200
1600
2000
400
800
1200
1600
2000
2400
2800
Grafik : 3p + 2b = 4.800
pensil
buku
(800,1200)

4. ◦ Grafik y = ax + c adalah merupakan garis lurus dan
berpotongan dengan sumbu y dititik (0,c)
Contoh 1 :
Gambarlah grafik : y = 2x + 6
Jawab :
Perpotongan dengan sumbu
y adalah di titik (0,6)
Jika y = 0 maka :
0 = 2x + 6
-2x = 6
x = -3
Titik potong dengan
sumbu X di titik (-3,0)
1 2 4 5
3
X
Y
0
-2 -1
-3
-4
-5
2
1
3
4
5
6
7
(0,6)
-2
-1
-3
(-3,0)
y = 2x + 6

5. Contoh 2 :
Gambarkan grafik garis yang persamaannya x + y = 5
Jawab :
Untuk titik ke 1 :
x = 0
x + y = 5
↔ 0 + y = 5
↔ y = 5
Untuk titik ke 2 :
x = 4
↔ 4 + y = 5
↔ y = 5 – 4
↔ y = 1
(0,5)
(4,1)
X
0
-2 -1
-3 1 2 4 5
3 7
6
2
1
3
4
5
6
Y
-2
-1
-3
(0,5)
(4,1)

6. Contoh 3 :
Gambarkan grafik garis yang persamaannya 2x – y = 6
Jawab :
Titik ke 1 :
x = 0
2x – y = 6
↔ 0 – y = 6
↔ y = -6
Titik ke 2 :
y = 0
↔ 2x – 0 = 6
↔ 2x = 6
↔ x = 3
(0,-6)
(3,0)
X
0
-4 -3 -2 -1 2 3
1 5
4
(0,-6)
(3,0)
1
2
Y
3
-2
-3
-1
-5
-4
-6
-7

7. Latihan :
Gambarlah grafik dari :
1. x = -3
2. y = 5
3. y = x + 3
4. x + 2y = -4
5. 2y = 6x – 9
6. 5x – 2y = -10
7. 3x + 4y – 12 = 0

8. PERSAMAAN YANG EKIVALEN
◦ Dua Persamaan yang ekivalen adalah persamaan yang maksud dan artinya sama
tetapi beda penulisannya.
Contoh 1 :
Harga : 3 pensil + 4 buku = Rp 15.000 ,
Harga : 6 pensil + 8 buku = Rp ………
Jadi Persamaan : 3 pensil + 4 buku = Rp 15.000 ekivalen dengan
6 pensil + 8 buku = Rp 30.000
Atau ditulis dengan singkat seperti berikut ini :
2p + 4b = 15.000 ekivalen dengan 6p + 8b = 30.000
30.000
Dikali 2 , hasilnya

9. Contoh 2 :
Rumus menghitung keliling persegi panjang adalah : K = 2p + 2l
Bila diketahui lebar dan Keliling , bagaimana rumus menentukan
panjangnya?
Jawab :
↔ K = 2p + 2l
↔ 2p + 2l = K
↔ 2p = K – 2l
↔ p = ½ (K – 2l)
Dari jawaban itu dapat dilihat bahwa :
1). K = 2p + 2l
2). 2p + 2l = K
3). 2p = K – 2l
4). p = ½ (K – 2l)
Semua merupakan
persamaan yang
Ekivalen

10. Contoh 3 :
Diketahui persamaan : 4x – 8y = 20
Manakah persamaan dibawah ini yang ekivale dengan
persamaan tersebut?
a. 2x – 4y = 10 b. x – 2y = 20 c. x – 2y = 5
d. 12x – 24y = 60 e. 4x + (-8y) = 20 f. 20 = 4x + (-8y)
g. -4x + 8y = -20 h. -4x – 8y = 20 i. -x + 2y = -5
j. 4x = 20 – 8y k. 4x = 20 + 8y l. 8y + 20 = 4x
m. 8y = 20 – 4x n. 8y = 4x – 20 o. x – 5 = 2y
p. x = 2y + 5 q. y = 4x – 20 r. y = 0,5x – 2,5

11. Yang Ekivalen dengan 4x – 8y = 20 adalah persamaan :
a. 2x – 4y = 10 c. x – 2y = 5
d. 12x – 24y = 60 e. 4x + (-8y) = 20
f. 20 = 4x + (-8y) g. -4x + 8y = -20
i. -x + 2y = -5 k. 4x = 20 + 8y
l. 8y + 20 = 4x n. 8y = 4x – 20
o. x – 5 = 2y p. x = 2y + 5
r. y = 0,5x – 2,5

12. B. GRADIEN
A. PENGERTIAN GRADIEN
◦ Gradien adalah suatu bilangan yang menyatakan
kemiringan suatu garis.
◦ Jika Gradien Positif , maka garisnya miring ke kanan
dan bila Gradien Negatif , maka garisnya miring ke kiri.
◦ Gradien suatu garis tergantung kepada persamaan
garis atau gambar garis tersebut.
◦ Menentukan gradien suatu garis lurus bila diketahui
persamaannya adalah sebagai berikut :
1. Jika persamaannya y = mx + c , Gradiennya = m
2. Jika persamaannya by = ax + c , Gradiennya =
3. Persamaannya ax + by = c
4. Persamaannya ax + by + c = 0
a
b
a
b
Gradiennya =

13. Menentukan Nilai Gradien Suatu
Garis Lurus
(i). Menurut Persamaannya
Contoh 1 :
Tentukanlah Gradien Garis jika persamaannya :
a. y = 3x + 1 b. y = 3x – 1
c. 2y = 8x d. ½y = -4x – 1
Jawab :
a. Gradien = m = 3
b. Gradien = m = 3
c. Gradien = m = 8/2 = 4
d. Gradien = m = -4 : ½
= -8

14. Contoh 2 :
Tentukan gradien garis jika persamaannya :
a. 5x + 2y = 8 b. y – 7x = 4 c. 4x – 3y + 2 = 0
Jawab :
Cara I : Dengan merubah bentuk persamaannya
a. 5x + 2y = 8
↔ 2y = 8 – 5x
↔ 2y = -5x + 8
↔ y = -21/2x + 4
Maka Gradien = m = -21/2
b. y – 7x = 4
↔ y = 4 + 7x
↔ y = 7x + 4
Maka Gradien = 7
c. 4x – 3y + 2 = 0
↔ -3y = -4x – 2
↔ y = 4/3x – 2/3
Maka Gradien = m = 4/3

15. Cara II : Menggunakan Rumus
a. 5x + 2y = 8
a = 5 , b = 2
Gradien = m = - a/b
= - 5/2
= -21/2
b. y – 7x = 4
-7x + y = 4
a = -7 , b = 1
Gradien = m = - a/b
= - (-7)/1
= 7
c. 4x – 3y + 2 = 0
a = 4 , b = -3
Gradien = m = - a/b
= - 4/-3
= 4/3

16. (ii). Menentukan Gradien Garis Lurus dari Grafiknya
Bila persamaan suatu garis :
y = 2x – 6 ,
maka grafiknya adalah seperti
gambar di kanan ini
Gradien garis itu = m = 2
Gradien menurut Grafik :
Kita tentukan 2 titik sembarang
pada garis tersebut , misalnya titik
A dan B , lalu dikanan A , tepat
dibawah B kita buat titik C.
Maka Panjang AC = 3 = Komponen x
dan panjang CB = 6 = komponen y
Jadi Gradiennya adalah :
m =
X
0 3
(0,-6)
(3,0)
Y
-6
3
6
A
B
C
Bagaimana kita menunjukkan
gradien itu pada Grafiknya ?
6
3 = 2

17. Untuk Menentukan Gradien Suatu Garis yang grafiknya
diketahui adalah : Gradien = m =
Contoh 1 :
Perhatikan gambar dikanan ini!
Tentukan gradien masing-
masing garis tersebut!
Jawab :
mg = 4/1 = 4
ml = 5/-2 = -21/2
Mk = 2,5/-1 = -21/2
g
l k
x
y
1
4
-2
5
Komponen y
Komponen x
0
Dua garis sejajar
selalu mempunyai
gradien yang sama.

18. Contoh 2 :
a. Tentukanlah Gradien masing-masing garis dibawah ini!
b. Tentukan hasil dari : mPQ x mRS !
Jawab :
a. (i). mAB =
(ii). mCD =
(iii). mKL =
(iv). mMN =
(v). mPQ =
(vi). mRS =
b. mPQ x mRS =
= -1
A B
C D
K
L
M
N
P
Q
R
S
-2
3
3
2
2
3
3
-2 = - 3
2
3
2
x (- )
2
3
0
4 = 0
0
7 = 0
5
0 = …?
3
0 = …?

19. Catatan :
◦ Gradien suatu garis tidak dipengaruhi oleh
panjang garis tersebut tetapi tergantung
kepada kemiringannya
◦ Setiap Garis yang Mendatar (Horizontal)
Gradiennya selalu 0 (nol).
◦ Setiap Garis yang Vertikal Gradiennya tidak
terdefinisikan.
◦ Jika Dua Garis Saling Tegak Lurus , maka Hasil
Kali Gradien Kedua garis itu selalu = -1

20. C. PENGGUNAAN GRADIEN
(i). Untuk Menggambar Grafik.
Contoh 1 :
Gambarlah grafik garis
y = 2x + 6
Jawab :
y = 2x + 6
Maka Gradiennya = m = 2
Jika y = 0
↔ 0 = 2x + 6
↔ -2x = 6
↔ x = -3
Jadi garis itu melalui titik (-3,0)
1 2 4 5
3
X
Y
0
-2 -1
-3
-4
-5
2
1
3
4
5
6
7
-2
-1
-3
1
2
(-3,0)
y = 2x + 6

21. Contoh 2 :
Gambarlah grafik dari : x + y = 5
Jawab :
Jika x = 4
↔ x + y = 5
↔ 4 + y = 5
↔ y = 5 – 4
↔ y = 1
Garis itu melalui (4,1)
Gradiennya = - 1 -2 -1
X
0 1 2 4 5
3 6
2
1
3
4
5
6
Y
-2
-1
-3
(4,1)
3

22. Contoh 3 :
Bahan untuk diskusi kelompok :
Dengan terlebih dahulu membuat sketsanya (gambarnya,
tentukanlah gradien garis yang melalui titik :
a. (2,1) dan (5,10) b. (1,0) dan (0,5)
c. (12,3) dan (22,1) d. (0,0) dan (1,2)
Kemudian berdasarkan jawaban yang didapat buatlah
suatu kesimpulan , yaitu suatu aturan atau rumus
menentukan gradien garis yang melalui dua titik.

23. Jika suatu garis melalui titik (x1,y1) dan (x2,y2) , maka
Gradien garis itu dapat ditentukan dengan cara :
Gradien = m =
y2 – y1
x2 – x1

24. (ii). Menentukan persamaan garis
Contoh 1 :
Diketahui suatu garis dengan gradien = 2 dan melalui titik (0,4).
Tentukanlah persamaan garis itu!
Jawab :
Misalkan persamaan itu :
y = mx + c → Gradien = m dan berpotongan dengan sb y
di titik (0,c)
Gradien = m = 2 dan melalui titik (0,4)
Maka persamaan garis itu adalah :
y = 2x + 4

25. Jika suatu garis melalui titik (x1 ,y1) dan gradien = m ,
maka persamaan garis itu dapat dientukan dengan
rumus :
y – y1 = m(x – x1)
Contoh 2 :
Tentukanlah Persamaan garis yang melalui titik (2,1)
dan (3,5)!

26. Jawaban Contoh 2 :
Garis melalui titik (2,1) dan (3,5)
Maka : x1 = 2 , y1 = 1
x2 = 3 , y2 = 5
Gradien = m =
=
m = 4
y – y1 = m(x – x1)
y – 1 = 4(x – 2)
y – 1 = 4x – 8
y = 4x – 7
y2 – y1
x2 – x1
5 – 1
3 – 2
Jadi persamaan garis itu adalah : y = 4x – 7