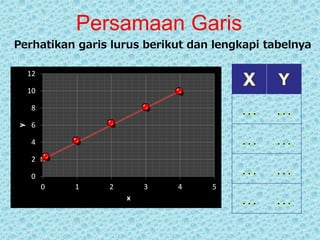
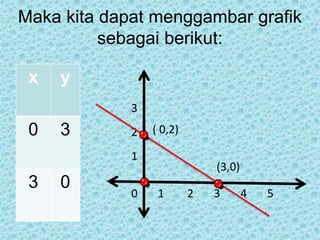
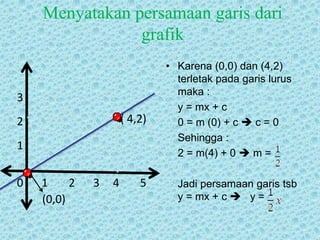
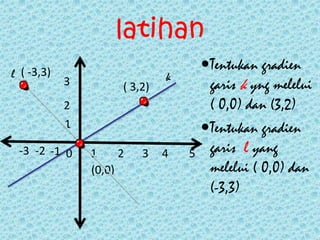
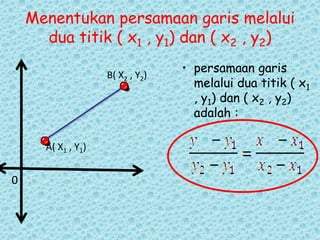
Dokumen tersebut membahas tentang persamaan garis lurus dan gradien. Secara singkat, dibahas tentang hubungan antara nilai x dan y pada garis lurus yang ditulis dalam persamaan y = mx + c, dan cara menentukan gradien baik dari persamaan maupun dari grafik.

1. SMA YABAKII
Imam ghozali

2. Persamaan Garis
Perhatikan garis lurus berikut dan lengkapi tabelnya
12
10
8
6
4
2
0
0 1 2 3 4 5
y
x

3. Bagaimana Hubungan nilai x dan
y dari grafik?
• Hubungan nilai x dan y pada garis lurus
diatas adalah
Y = 2x + 2
• Secara umum dapat ditulis : ax + by = c
dengan a,b,c bilangan real a,b,c ≠ 0
• Persamaan y = 2x + 2 disebut
persamaan garis lurus

4. Persamaan garis juga dapat ditulis dalam
bentuk:
y = m x + c
m dan c adalah suatu konstanta

5. Menggambar grafik persamaan
garis lurus y = mx +c pada bidang
kartesius
Gambar grafik
persamaan garis
lurus 2x + 3 y = 6
• Untuk x = 0 maka
2 (0) + 3y = 6
3y = 6
y =2
• Untuk y = 0 maka
2x+ 3(0) = 6
2x = 6
x = 3
• Maka diperoleh tabel :
x y
0 3
3 0

6. Maka kita dapat menggambar grafik
sebagai berikut:
x y
0 3
3 0
3
2
1
(3,0)
( 0,2)
0 1 2 3 4 5

7. Menyatakan persamaan garis dari
grafik
• Karena (0,0) dan (4,2)
terletak pada garis lurus
maka :
y = mx + c
0 = m (0) + c  c = 0
Sehingga :
2 = m(4) + 0  m =
Jadi persamaan garis tsb
y = mx + c  y =
3
2
1
0 1 2 3 4 5
(0,0)
( 4,2)

8. Gradien
Definisi :
• Misalkan tangga
dianggap garis lurus
maka nilai
kemiringan tangga
dapat ditentukan
dengan perbandingan
tingi tembok dengan
jarak kaki tangga dari
tembok
 Kemirngan tangga
tersebut disebut
Gradien

9. • Atau dapat di simpulkan :
Gradien adalah bilangan yang
menyatakan kecondongan suatu garis
yang merupakan prbandingan antara
komponen y dan komponen x
y Gradien= • Garis dengan
x
persamaan y = mx
Memiliki gradien m

10. Menentukan gradien bila diketahui
persamaan ax + by = c
• Telah kita ketahui bahwa persamaan
y = mx + c memiliki gradien m
• Maka bila diketahui persamaan ax+by =c
diubah menjadi y = mx + c
• ax + by = c
by = -ax + c
y = +
Gradien
• Kesimpulan:
• Gardien Persamaan
garis ax + by = c
• Adalah

11. latihan
1. Tentukan gradien dari persamaan garis
berikut
a. 2y = 5x -1
b. 3x – 4 y = 10

12. Menentukan gradien dari
grafik • Gradien garis yang
melalui titik ( 0,0)
dan titik (x,y)
• Maka gradienya
adalah :
• m =
3
2
1
0 1 2 3 4 5
(0,0)
( 4,2)
(x,y)

13. latihan
Tentukan gradien
garis k yng melelui
( 0,0) dan (3,2)
Tentukan gradien
garis l yang
melelui ( 0,0) dan
(-3,3)
l ( -3,3) k
3
2
1
0 1 2 3 4 5
(0,0)
( 3,2)
-3 -2 -1

14. Menentukan gradien yang melalui dua
titik ( X1 , Y1) dan ( X2 , Y2)
• Gradien garis
yang melalui
titik ( x1 , y1) dan
( x2 , y2) adalah:
0
A
( X1 , Y1)
B( X2 , Y2)
( y2 , y1)
y2
y1
( x2 , x1)
x2
x1

15. latihan
• Tentukan gradien garis yang memalui :
a. A(1,2) dan B (3,0)
b. C ( -3,1) dan D ( -2, -5)

16. Menentukan garis yang melalui sebuah titik (
x1 , y1) dengan gradien m
Untuk menentukan
persamaan garis
tersebut perhatikah
langkah berikut :
A. Subsitusikan titik ( x1 ,
y1) ke persamaan y=
mx+c
y = m x + c
y 1 = m x1 + c
c = y1 - mx1
B.Subsitusikan nilai c ke
persamaan y = mx+c
y = mx + c
y = mx + y1 - mx1
y – y1 = mx – mx1 m
y – y1 = m ( x – x1 )
Jadi persamaan garis melalui titik
( x1 , y1) dengan gradien m adalah
y – y1 = m ( x – x1 )

17. Latihan soal
1. Tentukan persamaan garis yang
melalui titik ( 3, 5 ) dan
bergradien ½
2. Tentukan persamaan garis
melalui titik ( -2,3) yang
bergradien 2

18. Menentukan persamaan garis melalui
dua titik ( x1 , y1) dan ( x2 , y2)
• persamaan garis
melalui dua titik ( x1
, y1) dan ( x2 , y2)
adalah :
0
A( X1 , Y1)
B( X2 , Y2)

19. contoh
Tentukan persamaan
garis lurus yang melalui
titik ( - 3, 5) dan (-2, -3)
• ( - 3, 5) dan (-2, -3)
( x1 , y1) dan ( x2 , y2)
• Persamaan :
• Kita kali silang kedua
ruas :
-5( y + 5 ) = 2 ( x – 3 )
- 5y – 25 = 2x – 6
- 5y = 2x –6 + 25
- 5y = 2x + 19
• Jadi persamaan garis
melalui titik ( - 3, 5)
dan (-2, -3) adalah:
- 5y = 2x + 19

20. Latihan soal
1. Tentukan persamaan garis yang melalui
titik (0,1) dan (1, -6)
2. Garis yang melalui titik ( 2,3) dan (1,
0) persamaan garisnya adalah..

21. Selamat Belajar