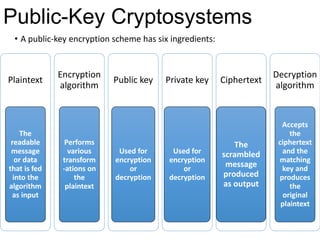
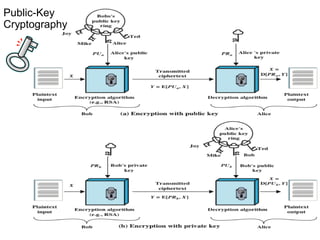
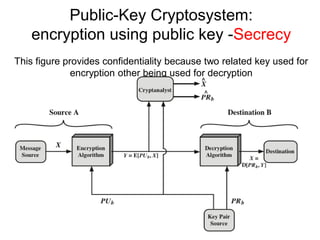
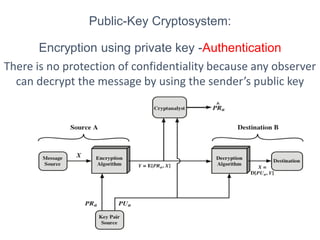
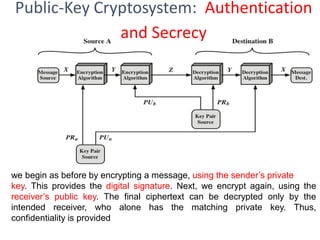
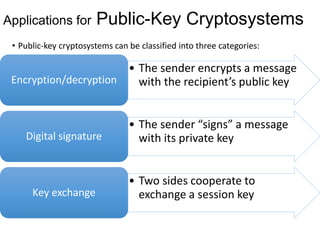
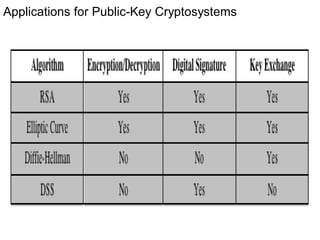
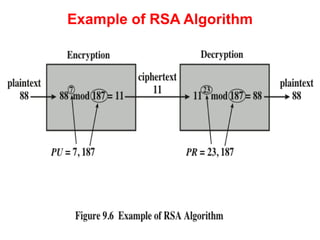
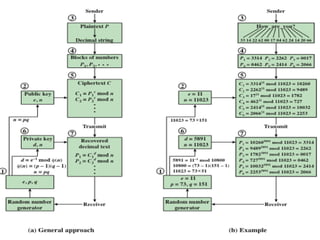
Public Key Cryptography (PKC) is an encryption method utilizing a pair of public and private keys for secure communications. The document explains the principles, requirements, and applications of PKC, including the RSA algorithm, which is widely used for encrypting messages and protecting confidentiality. Additionally, it covers various types of attacks on RSA and the use of Optimal Asymmetric Encryption Padding (OAEP) for enhanced security.

1. NETWORK SECURITY
Name of the Staff : M.FLORENCE DAYANA M.C.A.,M.Phil.,(Ph.D).,
Head, Dept. of CA
Bon Secours College For Women
Thanjavur.
Class : II MSc., CS
Semester : III
Unit : II
Topic : Public Key Cryptography
2/15/2019 1

2. Public key Cryptography
•Public key cryptography (PKC) is
an encryption technique that uses a paired
public and private key algorithm for secure
data communication.
•A message sender uses a recipient's public
key to encrypt a message.
•To decrypt the sender's message, only the
recipient's private key may be used.

3. Principles of Public-Key Cryptosystems
• The concept of public-key cryptography evolved from an
attempt to attack two of the most difficult problems
associated with symmetric encryption:
• The communicants already shares a key or someone has been
distributed the key.
• How to secure communications in general without having to trust a
KDC with your key
Key distribution
• How to verify that a message comes intact from the claimed sender
Digital signatures

4. Public-Key Cryptosystems
• A public-key encryption scheme has six ingredients:
Plaintext
The
readable
message
or data
that is fed
into the
algorithm
as input
Encryption
algorithm
Performs
various
transform
-ations on
the
plaintext
Public key
Used for
encryption
or
decryption
Private key
Used for
encryption
or
decryption
Ciphertext
The
scrambled
message
produced
as output
Decryption
algorithm
Accepts
the
ciphertext
and the
matching
key and
produces
the
original
plaintext

5. Public-Key
Cryptography

6. Conventional and Public-Key Encryption

7. Public-Key Cryptosystem:
encryption using public key -Secrecy
This figure provides confidentiality because two related key used for
encryption other being used for decryption

8. Public-Key Cryptosystem:
Encryption using private key -Authentication
There is no protection of confidentiality because any observer
can decrypt the message by using the sender’s public key

9. Public-Key Cryptosystem: Authentication
and Secrecy
we begin as before by encrypting a message, using the sender’s private
key. This provides the digital signature. Next, we encrypt again, using the
receiver’s public key. The final ciphertext can be decrypted only by the
intended receiver, who alone has the matching private key. Thus,
confidentiality is provided

10. Applications for Public-Key Cryptosystems
• Public-key cryptosystems can be classified into three categories:
• The sender encrypts a message
with the recipient’s public keyEncryption/decryption
• The sender “signs” a message
with its private keyDigital signature
• Two sides cooperate to
exchange a session keyKey exchange

11. Applications for Public-Key Cryptosystems

12. Public-Key Requirements
Conditions that these algorithms must fulfil:
1. It is computationally easy for a party B to generate a pair (public-
key PUb, private key PRb)
2. It is computationally easy for a sender A, knowing the public key
and the message to be encrypted, to generate the corresponding
ciphertext
3. It is computationally easy for the receiver B to decrypt the
resulting ciphertext using the private key to recover the original
message
4. It is computationally infeasible for an adversary, knowing the
public key, to determine the private key.
5. It is computationally infeasible for an adversary, knowing the
public key and a ciphertext, to recover the original message.
6. The two keys can be applied in either order.

13. Public-Key Requirements
trap-door one-way function
•A trapdoor function is a function that is easy to
compute in one direction, yet difficult to compute in
the opposite direction (finding its inverse) without
special information, called the "trapdoor". Trapdoor
functions are widely used in cryptography.
•Y = f(X) easy
•X = f–1(Y) infeasible

14. Public-Key Requirements
A trap-door one-way function is a family of
invertible functions fk, such that
Y = fk(X) easy, if k and X are known
X = fk
–1(Y) easy, if k and Y are known
X = fk
–1(Y) infeasible, if Y known but k not
known
A practical public-key scheme depends on a
suitable trap-door one-way function

15. Rivest-Shamir-Adleman (RSA) Scheme
•RSA is the algorithm used by modern computers to
encrypt and decrypt messages. It is an asymmetric
cryptographic algorithm.
•Asymmetric means that there are two different keys.
This is also called public key cryptography, because
one of them can be given to everyone. The other key
must be kept private.
•One of the first successful responses to the challenge
was Developed in 1977 at MIT by Ron Rivest, Adi
Shamir & Len Adleman

16. RSA Algorithm
•Plaintext is encrypted in blocks with each block having a
binary value less than some number n
•Encryption and decryption are of the following form, for
some plaintext block M and cipher text block C
C = Memod n
M = Cd mod n = (Me)d mod n = Med mod n
•Both sender and receiver must know the value of n
•The sender knows the value of e, and only the receiver knows
the value of d
•This is a public-key encryption algorithm with a public key
of PU={e,n} and a private key of PR={d,n}

17. Algorithm Requirements
• For this algorithm to be satisfactory for public-key encryption, the
following requirements must be met:
1. It is possible to find values of e, d, n
such that Med mod n = M for all M<n
2. It is relatively easy to calculate Me mod n
and Cd mod n for all values of M < n
3. It is infeasible to determine d given e
and n

18. RSA Algorithm

19. Example of RSA Algorithm

21. The Security of RSA
Five possible
approaches to
attacking RSA
are:
Brute force
• Involves trying all
possible private
keys
Mathematical attacks
• There are several
approaches, all
equivalent in effort to
factoring the product
of two primes
Timing attacks
• These depend on the
running time of the
decryption algorithm
Hardware fault-based
attack
• This involves inducing
hardware faults in the
processor that is
generating digital
signatures
Chosen ciphertext
attacks
• This type of attack
exploits properties
of the RSA algorithm

22. Optimal Asymmetric Encryption Padding
(OAEP)
•Optimal Asymmetric Encryption Padding
(OAEP) is a padding scheme often used
together with RSA encryption.
•The OAEP algorithm is a form of Feistel
network which uses a pair of random oracles
G and H to process the plaintext prior to
asymmetric encryption.

23. Optimal
Asymmetric
Encryption
Padding
(OAEP)

24. Figure shows OAEP encryption.
1. As a first step, the message M to be encrypted is padded.
A set of optional parameters, P, is passed through a hash
function, H.
2. The output is then padded with zeros to get the desired length in the
overall data block (DB).
3.Next, a random seed is generated and passed through
another hash function, called the mask generating function (MGF).
4. The resulting hash value is bit-by-bit XORed with DB to produce a
maskedDB.
5.The maskedDB is in turn passed through the MGF to form a hash that is
XORed with the seed to produce the masked seed.
6. The concatenation of the masked-seed and the maskedDB forms the
encoded message EM.
Note that the EM includes the padded message, masked by the seed, and
the seed, masked by the maskedDB. The EM is then encrypted using
RSA.