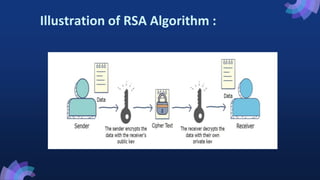
The document summarizes the RSA cryptosystem. It begins with an introduction to cryptography and the two types: symmetric and asymmetric. RSA is an asymmetric algorithm that uses a public and private key pair. The document provides an illustration of how RSA works and describes the key generation process where two prime numbers are multiplied to generate the modulus and keys. It also provides an example of encrypting a plaintext message using a public key and decrypting the ciphertext with a private key. Advantages of RSA include security while disadvantages are slower speed and large key sizes.

1. RSA
Cryptosystem
Presented By:
Anurag Admuthe (2253009)
Yash Adashetty (2103028)
Under The Guidance Of : Prof. G. G. Shingan

2. Index :
 Introduction to Cryptography
 Features of cryptography
 RSA Algorithm
 RSA and DRSA
 Algorithm for generating the keys
 Encryption & Decryption
 Example
 Advantages and Disadvantages
 References

3. Introduction:
● Cryptography:
 In digital Communication, Security is implemented using cryptography. Cryptography
is a technique of converting message into ciphertext for hiding confidential data.
 There are two types of cryptography:
1)Symmetric key cryptography
2)Asymmetric key cryptography
 In 1971, Diffie Hellman key exchange program was introduced for Asymmetric key
cryptography.
 RSA Algorithm was one of the first algorithms implemented in Asymmetric key
cryptography.

4. Features of cryptography :
● Confidentiality: Information can only be accessed by the person
for whom it is intended and no other person except him can
access it.
● Integrity: Information cannot be modified in storage or transition
between sender and intended receiver without any addition to
information being detected.
● Non-repudiation: The creator/sender of information cannot deny
his intention to send information at later stage.
● Authentication: The identities of sender and receiver are
confirmed. As well as destination/origin of information is
confirmed.

5. ● The RSA algorithm is an asymmetric cryptography algorithm; this means that it uses
a public key and a private key (i.e. two different, mathematically linked keys). As their
names suggest, a public key is shared publicly, while a private key is secret and must
not be shared with anyone.
● The RSA algorithm is named after those who invented it in 1978: Ron Rivest, Adi
Shamir, and Leonard Adleman.
● The following illustration highlights how asymmetric cryptography works:
RSA (Rivest-Shamir-Adleman) Algorithm :

6. Illustration of RSA Algorithm :

7. RSA and Dependent RSA(DRSA) :
 DRSA is a variant of RSA, which overcomes the semantic security
problem of data-leak in RSA.
 This process of cryptography contains 3 phases,
1. Key Generation
2. Encryption
3. Decryption

8. Algorithm for generating the keys :
In the phase of key generation,
• Step-1 : Using some primality tests, two large distinct prime
numbers, p and q are generated and keep the values of p and q as
his private keys.
• Step-2 : Calculate n = p*q and publish the value of n as public key.
• Step-3 : Calculate totient function Φ(n) = (p – 1)(q – 1).
• Step-4 : Choose one random value of e, such that GCD(Φ(n), e) = 1.
• Step-5 : Bob computes d, where d = e-1 (mod Φ(n)).
• Step-6 : Choose one hash function h to be used in the scheme.
Encryption & Decryption
● Encryption : c = m ^ e mod n
● Decryption : m = c ^ d mod n

9. Example :
Select two large prime numbers, p, and q.
p = 7
q = 11
Step 2: Multiply these numbers to find n = p x q, where n is called the modulus for
encryption and decryption.
First, we calculate
n = p x q
n = 7 x 11
n = 77
Step 3: Choose a number e less that n, such that n is relatively prime to (p - 1) x (q -
1). It means that e and (p - 1) x (q - 1) have no common factor except 1. Choose
"e" such that 1<e < φ (n), e is prime to φ (n), gcd (e, d (n)) =1.
Second, we calculate
φ (n) = (p - 1) x (q-1)
φ (n) = (7 - 1) x (11 - 1)
φ (n) = 6 x 10
φ (n) = 60

10. Example :
Let us now choose relative prime e of 60 as 7.
Thus the public key is <e, n> = (7, 77)
Step 4: A plaintext message m is encrypted using public key <e, n>. To find ciphertext
from the plain text following formula is used to get ciphertext C.
To find ciphertext from the plain text following formula is used to get ciphertext C.
C = me mod n
C = 97 mod 77
C = 37
Step 5: The private key is <d, n>. To determine the private key, we use the following
formula d such that:
De mod {(p - 1) x (q - 1)} = 1
7d mod 60 = 1, which gives d = 43
The private key is <d, n> = (43, 77)
Step 6: A ciphertext message c is decrypted using private key <d, n>. To calculate plain
text m from the ciphertext c following formula is used to get plain text m.
m = cd mod n
m = 3743 mod 77
m = 9
In this example, Plain text = 9 and the ciphertext = 37

11. Advantages :
 Security: RSA algorithm is considered to be very secure and is widely used for
secure data transmission.
 Public-key cryptography: RSA algorithm is a public-key cryptography algorithm,
which means that it uses two different keys for encryption and decryption. The
public key is used to encrypt the data, while the private key is used to decrypt
the data.
Disadvantages
 Slow processing speed: RSA algorithm is slower than other encryption
algorithms, especially when dealing with large amounts of data.
 Large key size: RSA algorithm requires large key sizes to be secure, which
means that it requires more computational resources and storage space.

12. Reference :
On Using The First Variant of Dependent RSA Encryption Scheme
to Secure Text: A Tutorial
by : D Rachmawati and M A Budiman 2020