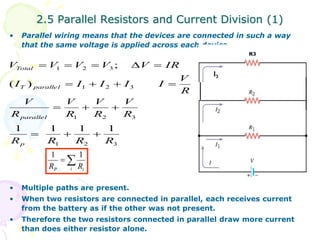
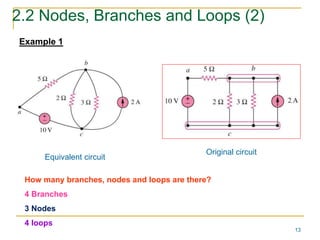
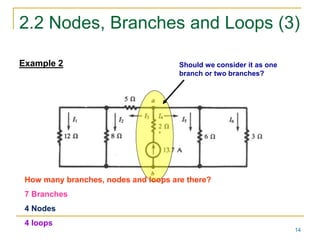
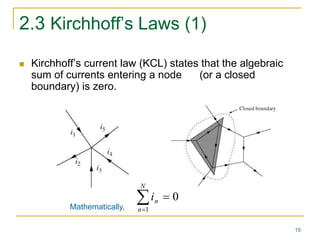
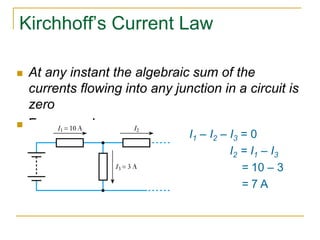
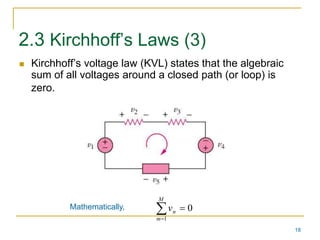
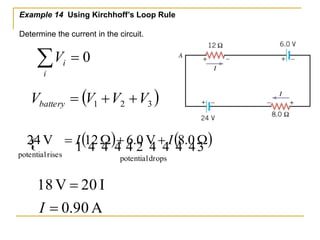
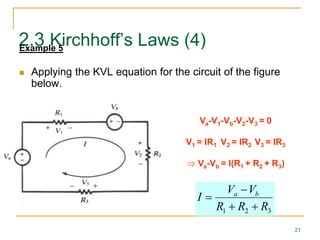
This document provides an overview of basic circuit laws including Ohm's law, Kirchhoff's laws, and analysis of series and parallel circuits. Ohm's law states that voltage across a resistor is proportional to current through the resistor. Kirchhoff's laws include the junction rule that the total current entering a node equals the total leaving, and the loop rule that the sum of all potential differences around a closed loop is zero. Series and parallel circuits are analyzed using concepts like equivalent resistance, voltage division, and current division. Examples are provided to demonstrate applying these circuit analysis techniques.

1. Lecture 2
Basic Circuit Laws

2. 2
Basic Circuit Laws
2.1 Ohm’s Law.
2.2 Nodes, Branches, and Loops.
2.3 Kirchhoff’s Laws.
2.4 Series Resistors and Voltage Division.
2.5 Parallel Resistors and Current Division.
2.6 Wye-Delta Transformations.

3. 3
2.1 Ohms Law (1)
• Ohm’s law states that the voltage across
a resistor V(v) is directly proportional to
the current I(A) flowing through the
resistor.
V  V 
V
ab a b
V 
I
ab
R
R


constant of proportionality
Resistance
V 
IR
IR
ab


• When R=0 short circuit
• When R=  open circuit.
a
b

4. 4
2.1 Ohms Law (2)
• Conductance is the ability of an element to
conduct electric current; it is the reciprocal
of resistance R and is measured in siemens.
i
v
1
G  
R
• The power dissipated by a resistor:
v
R
p vi i R
2
2   

5. 2.4 Series Resistors and Voltage
5
Division (1)
• Series: Two or more elements are in series if they
are cascaded or connected sequentially
and consequently carry the same current.
• The equivalent resistance of any number of
resistors connected in a series is the sum of the
individual resistances.
N

eq N n R R R R R

       
n
1
1 2
• The voltage divider can be expressed as
v
R
R R R
v
N
n

n      
1 2

6. 2.4 Series Resistors and Voltage Division
(1)
I I I I
series Total
  
( ) 1 2 3
V V V V
series Total
  
( ) 1 2 3
As the current goes through the circuit, the charges must USE ENERGY to get
through the resistor. So each individual resistor will get its own individual potential
voltage). We call this voltage drop.
V  V  V  V  V 
IR
series Total
( ) 1 2 3
( )
;
I R I R I R I R
T T series
R  R  R 
R
series

  
1 2 3
R R
s i
1 1 2 2 3 3
Note: They may use the
terms “effective” or
“equivalent” to mean
TOTAL!

7. Example
A series circuit is shown to the left.
a) What is the total resistance?
R(series) = 1 + 2 + 3 = 6W
b) What is the total current?
V=IR 12=I(6) I = 2A
c) What is the current across EACH
resistor?
They EACH get 2 amps!
d) What is the voltage drop across
each resistor?( Apply Ohm's law
to each resistor separately)
V1W(2)(1) 2 V V3W=(2)(3)= 6V V2W=(2)(2)= 4V
Notice that the individual VOLTAGE DROPS add up to the TOTAL!!

8. 2.5 Parallel Resistors and Current
8
Division (1)
• Parallel: Two or more elements are in parallel if
they are connected to the same two nodes and
consequently have the same voltage across them.
• The equivalent resistance of a circuit with
N resistors in parallel is:
1 1 1 1
      
R R R R
eq 1 2
N • The total current i is shared by the resistors in
inverse proportion to their resistances. The
current divider can be expressed as:
eq
v
i  
n R
n
n
iR
R

9. 2.5 Parallel Resistors and Current Division (1)
• Parallel wiring means that the devices are connected in such a way
that the same voltage is applied across each device.
V  V  V  V  V 
IR
1 2 3
;
   
1 2 3
V
R
V
  
R
V
R
1 2 3
Total
( )
T parallel
parallel
1 1 1 1
R R R R
1 2 3
V
1 1
• Multiple paths are present.
• When two resistors are connected in parallel, each receives current
from the battery as if the other was not present.
• Therefore the two resistors connected in parallel draw more current
than does either resistor alone.
R
V
R
I I I I I
p
  
R3

P i i R R
I3

10. Example 4
To the left is an example of a parallel circuit.
a) What is the total resistance?
1
1 1
  
1
1
   
0.454
0.454
R
P
1
9
7
5
P
p
R
R
2.20 W
V IR
 
8 I (R)
 
b) What is the total current?
3.64 A
c) What is the voltage across EACH resistor?
8 V each!
d) What is the current drop across each resistor?
(Apply Ohm's law to each resistor separately)
V IR
 
8
8
8
5 7 9 I I I
     
W 5
W 7
W 9
1.6 A 1.14 A 0.90 A
Notice that the
individual currents
ADD to the total.

11. 11
Gustav Kirchhoff
1824-1887
German Physicist

12. 2.2 Nodes, Branches and Loops (1)
12
 A branch represents a single element such as a
voltage source or a resistor.
 A node is the point of connection between two
or more branches.
 A loop is any closed path in a circuit.

13. 13
2.2 Nodes, Branches and Loops (2)
Example 1
Original circuit
Equivalent circuit
How many branches, nodes and loops are there?
4 Branches
3 Nodes
4 loops

14. 2.2 Nodes, Branches and Loops (3)
14
Example 2 Should we consider it as one
branch or two branches?
How many branches, nodes and loops are there?
7 Branches
4 Nodes
4 loops

15. 15
2.3 Kirchhoff’s Laws (1)
 Kirchhoff’s current law (KCL) states that the algebraic
sum of currents entering a node (or a closed
boundary) is zero.
0
 
1
N
n
n i
Mathematically,

16. Junction Rule
 Conservation of mass
 Electrons entering must
equal the electrons leaving
 The junction rule states
that the total current
directed into a junction
must equal the total current
directed out of the junction.

17. Kirchhoff’s Current Law
 At any instant the algebraic sum of the
currents flowing into any junction in a circuit is
zero
 For example
I1 – I2 – I3 = 0
I2 = I1 – I3
= 10 – 3
= 7 A

18. 18
2.3 Kirchhoff’s Laws (3)
 Kirchhoff’s voltage law (KVL) states that the algebraic
sum of all voltages around a closed path (or loop) is
zero.
 
Mathematically, 0
1
M
m
n v

19. Kirchhoff’s Voltage Law
 At any instant the algebraic sum of the
voltages around any loop in a circuit is zero
 For example
E – V1 – V2 = 0
V1 = E – V2
= 12 – 7
= 5 V

20. Example 14 Using Kirchhoff’s Loop Rule
Determine the current in the circuit.
 
i
 1(   )  2   (   )
24 V  I 12 W  6.0 V I 8.0 W
potential drops
potential rises
18 V 
20 I
I

0.90 A
i V 0
( ) 1 2 3 V V V V battery   

21. 21
2.3 Kirchhoff’s Laws (4) Example 5
 Applying the KVL equation for the circuit of the figure
below.
Va-V1-Vb-V2-V3 = 0
V1 = IR1 V2 = IR2 V3 = IR3
 Va-Vb = I(R1 + R2 + R3)
V 
V
I a b
R  R 
R
1 2 3 

22. Loop Rule
 The loop rule expresses conservation of
energy in terms of the electric potential.
 States that for a closed circuit loop, the total
of all potential rises is the same as the total of
all potential drops.