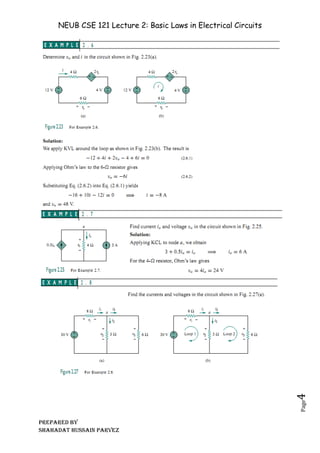
The document outlines essential electrical circuit laws, specifically Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL), necessary for circuit analysis. KCL states that the total current entering a node equals the total current leaving it, while KVL asserts that the sum of all voltages in a closed loop is zero. The document also discusses principles like voltage and current division for resistors in series and parallel configurations, and introduces concepts of circuit transformations like wye-delta transformation.